从f ′(x)=0谈起

唐 庚

(中国人民大学附属中学分校，100086)



从f ′(x)=0谈起

唐 庚

(中国人民大学附属中学分校，100086)

导数是解决函数图象、性质以及方程不等式等问题的有力工具,是数学高考重点之一.f ′(x)=0的根是利用导数分析函数性质过程中最为核心的量，它关联着函数的单调性、极值(最值)等,但某些函数的导数为零时,根不易求得,成为解题过程中的难点．我们举例探究对非常规零点的求解或使用,寻求恰当处理方式,以便对后续问题的解决铺平道路．

一、方程f ′(x)=0无实数根

例1 (2016年北京高考题)设函数f(x)=xea-x+bx，曲线y=f(x)在点(2,f(2))处的切线方程为y=(e-1)x+4.

(1)求a,b的值；

(2)求f(x)的单调区间.

解 (1)a=2,b=e(过程略).

(2)由(1)知f(x)=xe2-x+ex.

由f ′(x)=e2-x(1-x+ex-1)，知f ′(x)与1-x+ex-1同号.

令g(x)=1-x+ex-1,则

g′(x)=-1+ex-1.

易见g(x)在区间(-∞,1)上单调递减，

在区间(1,+∞)上单调递增，故g(1)=1是g(x)在区间(-∞,+∞)上的最小值,从而g(x)>0,x∈(-∞,+∞).

综上可知,f ′(x)>0,x∈(-∞,+∞),故f(x)的单调递增区间为(-∞,+∞).

评注 对于(2)，在得到f ′(x)=e2-x(1-x+ex-1)后,如果再令f ′(x)=0，则无法求出此方程的根,事实上此方程本就无解,即解集为空集.

若方程f ′(x)=0无实数根也就意味着y=f ′(x)图象与x轴无交点,即曲线y=f ′(x)恒在x轴上方(或者下方),也即f ′(x)>0(或者f ′(x)<0)恒成立，这时，问题可以转化为求函数y=f ′(x)的值域．

二、 方程f ′(x)=0有实根但不易求出,可以先变形再解方程

例2 已知函数f(x)=xln x.

(1)求曲线y=f(x)在点(1,f(1))处的切线方程;

(2)求证:f(x)≥x-1;

解 (1)(2)略.

显然，此时问题已经转化为只需讨论一个二次方程的根.

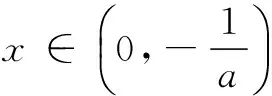
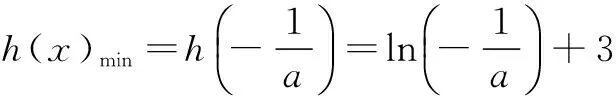
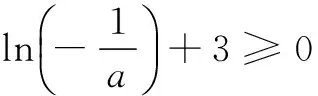
所以-e3≤a<0,a的最小值为-e3.

三、 f ′(x)=0有根但无法求出

例3 已知函数f(x)=xln x+ax2-1,且f ′(1)=-1.

(1)求f(x)的解析式;

(2)若对于任意x∈(0,+∞),都有f(x)-mx≤-1,求m的最小值;

(3)证明:函数y=f(x)-xex+x2的图象在直线y=-2x-1的下方.

解 (1)(2)略．

(3)问题等价于

f(x)-xex+x2+2x+1<0,

即要证xln x-xex+2x<0,

所以只要证 ex-ln x>2.

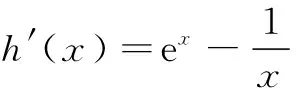
当x在定义域上变化时,h′(x)的变化情况如下:

x(0,x0)x0(x0,+∞)h'(x)-0+h(x)↘极小值↗

所以函数h(x)=ex-ln x的最小值为h(x0).

下面证明h(x0)>2.

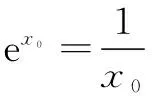
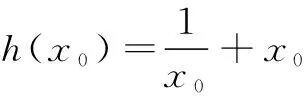
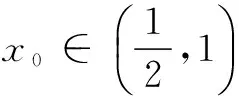
故函数y=f(x)-xex+x2的图象在直线y=-2x-1的下方.

评注 对某些导函数,我们可以通过零点存在定理判断其存在零点,但是无法获得零点的精确值．我们可以虚设零点,间接使用，常见方法是代换．将指数、对数或者三角函数式划归为代数式，通过恒等变换对极值问题进行转化.

四、 f ′(x)=0求出根后运算复杂

例4 设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R.

(1)求f(x)的单调区间;

(2)若f(x)存在极值点x0,且f(x1)=f(x0),其中x1≠x0,求证:

x1+2x0=3.

解 (1)求出函数的导数

f ′(x)=3(x-1)2-a.

分类讨论:①当a≤0时,有f ′(x)≥0恒成立,所以f(x)的单调增区间为(-∞,∞).

列表分析：

x-∞,1-3a3()1-3a31-3a3,1+3a3()f'(x)+0-f(x)单调增极大值单调减x1+3a31+3a3,+∞()f'(x)0+f(x)极小值单调递增

所以f(x)的单调递减区间为

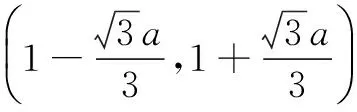
单调递增区间为

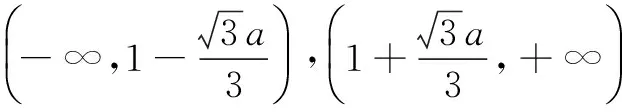
(2)由f(x)有极值点x0,结合(1)知a>0,且存在唯一实数x1满足f(x1)=f(x0),x1≠x0,故欲证x1+2x0=3等价于证明

x1=3-2x0，

即 f(x1)=f(3-2x0).

由f ′(x0)=0，得

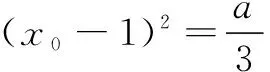
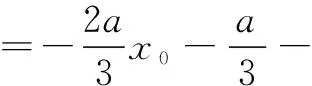
-a(2-2x0)-b

=f(x0),

且3-2x0≠x0,

故存在唯一实数满足f(x1)=f(x0),且x1≠x0,因此x1=3-2x0,所以

x1+2x0=3.

评注 如果f ′(x)=0是一个常见的二次方程,且只能利用求根公式得到两根,在进一步求值的过程中运算量大,问题求解难以完成．解决的基本思想仍是代换,有的是通过二次式配凑出三次式,有的是类似于解析几何中的设而不求,利用韦达定理将根转化成系数进行运算.

通过以上实例不难发现,f ′(x)=0(即导函数的零点)的求解过程中,我们的思维不应该仅仅停留在如何解出根,尤其是一些非常规方程,更应该从根是否存在,可否先转化,能否设而不求等角度入手,适当进行整体代换,突破解题瓶颈,回避繁杂运算,用创造型的思维,实现解题过程的跳跃式前进．