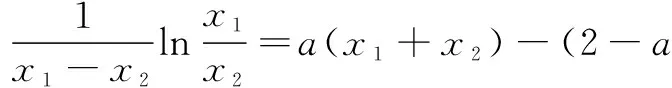求解不等式成立问题的常见策略

江志杰

(福建省惠安第三中学，362100)



求解不等式成立问题的常见策略

江志杰

(福建省惠安第三中学，362100)

众所周知,在全国高考或各地高三质检的压轴题中,有关不等式成立问题占据了半壁江山,这类题型最能有效地考查学生的数学思想方法、综合应用能力和学科核心素养,也是一份试卷精华创新之所在.笔者就不等式成立问题中函数模型的建构过程略谈一番体会.

一、参变分离原则

在含参数的不等式成立问题中,若不等式中含参数的部分容易“分离”,并且另一端的“无参”函数可求最值时,采用这种“分离参数法”的思路简洁通俗、直截了当.应该说,参变分离就是我们建构目标函数解决问题的一种典型做法.

例1 对一切x>0,不等式2xln x≥-x2+ax-3恒成立,求实数a的取值范围.

二、通性通法原则

研究形如“f(x)>g(x)”的不等式时,通常就是构造“差函数”F(x)=f(x)-g(x),分析该目标函数的单调性研究其极值、最值情况.然而在实际的函数导数压轴题中,所构造的“差函数”往往含有参数,这就给目标函数的单调性、极点、零点、最值等性质的研究带来不确定性,需要我们把握分类讨论的依据,罗列所有可能情形逐一分析,方能将目标函数的各种性态研究透彻,进而实现问题的化解.

例2 (2015年山东高考题)设函数f(x)=ln(x+1)+a(x2-x),其中a∈R.

(1)讨论函数f(x)极值点的个数,并说明理由;

(2)若∀x>0,f(x)≥0成立,求a的取值范围

解 (1)略.

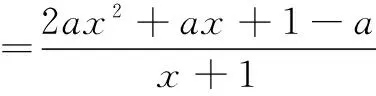
(i)当a∈[0,1]时,f ′(x)>0,f(x)在(0,+∞)内单调递增,f(x)>f(0)=0满足题意.

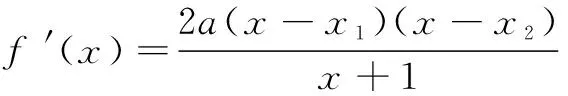
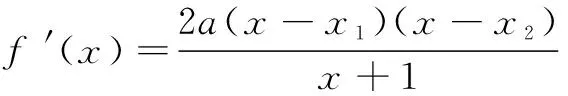
综上,a的取值范围为[0,1].

评注 对含参目标函数的单调性进行分析讨论是研究其最值、零点情况的基础程序,也是解决相应不等式问题的必由之路.因此,我们要充分利用导数工具将各式各样的函数模型淋漓尽致、形象自然地刻画出来，为化解抽象不等式提供具体生动的研究载体.

三、简约可行原则

笔者认为:在建构目标函数模型时,还应注意对所构造的函数要进行提炼、简化或变形,使所构造的目标函数模型优化有效,从而让问题的解决路径得以通畅顺达.

例3 (2015年四川高考题)已知函数f(x)=-2(x+a)ln x+x2-2ax-2a2+a,其中a>0.

(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;

(2)证明:存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在(1,+∞)内有唯一解.

解 (1)略.

(2)关键在于证明:存在a∈(0,1),使得f(x)在区间(1,+∞)内的最小值为0(且最小值点唯一)，为此需要先确定f(x)的单调性.

方法1 试图由

的符号确定f(x)的单调性将会极其困难.

求导得

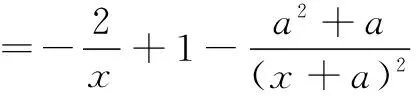
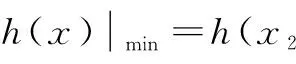
于是,问题又转化为证明存在a∈(0,1),使得h(x2)=0存在唯一实根.

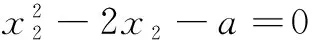
评注 基于原函数直接求导判断单调性较为困难,我们从原函数结构中分离提炼目标函数,使得利用导数探究函数性态的常规做法持续可行,将不等式问题自然转化为研究该目标函数,凸显了化繁为简、化难为易的解题原则.这说明研究函数一定要抓住其“关键所在”,构建函数一定要把握问题的“核心部位”,才能使目标函数的建构精准到位!

四、搭桥过渡原则

证明某些形如f(x)>g(x)的不等式成立时,常规构造差函数的做法有时未必奏效、甚至困在死胡同.此时我们可以考虑引入中间媒介h(x)作过渡,证明f(x)≥h(x)≥g(x)且两个等号不能同时成立.h(x)可根据f(x)、g(x)的图象特征或函数性态来确定.有时可能是一条隔离直线,也可能是个数值,关键视实际问题不断尝试、调整.

(1)求a,b;

(2)证明:f(x)>1.

分析 (1)a=1,b=2(解略).

五、设而不求原则

解决不等式成立问题时,经常让我们受困的是所建构的目标函数求导后仍是繁杂的超越函数,无法确定其零点,从而造成目标函数的单调性、极点、极值等也相应无法确定.为此,笔者提出构设导函数的辅助零点,突破导函数“无法求解”这一瓶颈,打通原函数研究的常规思路,巧妙利用导函数零点存在的等量关系进行代换,从而实现导函数零点的“设而不求”.

例5 若不等式x(1-k)+k+xln x>0对任意x>1均成立,求整数k的最大值.

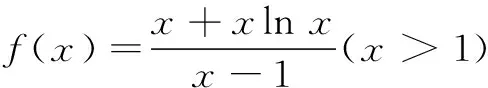
故整数k≤3,从而整数k的最大值为3.

六、一元归化原则

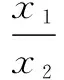
例6 (2011年辽宁高考题)已知函数

f(x)=ln x-ax2+(2-a)x.

(1)讨论f(x)的单调性;

(2)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f ′(x0)<0.

i)若a≤0,则f ′(x)>0,所以f(x)在(0,+∞)内单调递增;

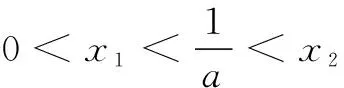
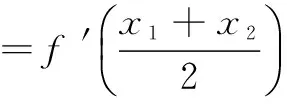
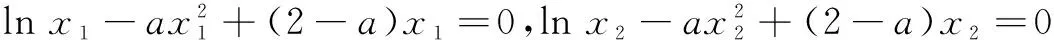
+(2-a)(x1-x2)=0,

变形整理，得