立体几何中的转化思想方法
马怡平●
江苏省常熟市尚湖高级中学(215500)
立体几何中的转化思想方法
马怡平●
江苏省常熟市尚湖高级中学(215500)
立体几何中蕴含着丰富的数学思想方法.求解立体几何问题时用得最多的是转化的思想方法,它可把陌生问题转化为熟悉问题,复杂问题转化为简单问题,从而实现问题解决.下面是常见的几种转化手段.
一、分割与补形
通过分割与补形,可把不规范、不易求解的几何体转化成规范的几何体,化生为熟,化难为易,实现突破.

例1 如图1,△ABC是边长为2的正三角形,AA1,BB1,CC1都与面ABC垂直,且AA1=3,BB1=2,CC1=1,求该几何体ABC-A1B1C1的体积V.

解法1 (分割法)如图2,过三点A、B、C1作平面,将这个不能直接求体积的几何体分割成两个可求体积的三棱锥C1-ABC和四棱锥C1-AA1B1B.





解法2 (补形法)由题设几何体的特征,将AA1,BB1,CC1分别接上1,2,3,构成正三棱柱ABC-A2B2C2,如图3.显然补上的几何体与原几何体是等积的,因此该正三棱柱的体积是原几何体体积的二倍.

二、顶点与底面
对于四面体(三棱锥)体积的求解,可认定某一个顶点为三棱锥的顶点,该顶点所对的面为底面,那么就可以用棱锥的体积公式计算了.由于顶点与底面选择的多样灵活性,会给解题带来方便.

例2 如图4,已知正方体ABCD-A1B1C1D1的棱长为2,E是BB1的中点,F是CD的中点,求三棱锥D1-A1EF的体积.
解 三棱锥D1-A1EF的底面积和高都难求得,变更顶点为F,则F所对底面A1ED1的面积不难求了.但F到底面A1ED1的距离仍比较难求,为此,取棱AB的中点G,易知GF∥A1D1,可推得GF∥面A1ED1,因此三棱锥F-A1ED1与三棱锥G-A1ED1等体积,但顶点G到面A1ED的距离仍不易求.再次变更顶点,以D1为顶点,A1EG为底面,显然三棱锥D1-A1EG的底面积、高都易求.因此,VD1-A1EF=VF-A1ED1=VG-A1ED1=VD1-A1EG.

三、平移与旋转
在难以直接求解的立体问题中,对某些几何元素作一些恰当的平移、转动等变换,转化为平面问题,是立体几何中解题的基本手法.
例3 设正三棱柱ABC-A1B1C1的棱长都是2.
(1)求异面直线CA1与AB1所成角的余弦值;
(2)设A1C1的中点是M,BB1的中点是N,求由M沿几何体表面到N的最短距离.

(2)由M沿几何体表面到N的最短距离,利用旋转法,将两个平面转动到同一个平面,转化为平面内两点间的距离.


四、平行与垂直
立体几何中研究的线与线、线与面,面与面的位置关系中,最基本,最常见的就是平行与垂直的关系.而平行与垂直关系却是相互依存的,把握它们之间的辩证关系进行恰当的转化,常可打开思路,顺利解题.
例4 设AB是异面直线AC与BD的公垂线段,AC⊥面α,BD⊥面β,α∩β=l,求证AB∥l.
▶
▶ 证法1 (用平行转化)如图7,由AC、AB确定平面γ,记γ∩α=CE.由



由AB、BD确定平面δ,记δ∩β=FD.同上可得AB∥
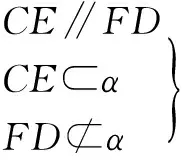



说明 证法1利用线与线平行的传递性,以平行类定理为主线来证明;而证法2却从垂直的角度来思考,构造出平面γ,利用AB、l同垂直于平面γ,获得结论.两种证法各展风采.
G632
B
1008-0333(2016)28-0045-02

