一道课本练习题的多视角求解

湖北省咸丰县第一中学(445600)

江 维●



一道课本练习题的多视角求解

湖北省咸丰县第一中学(445600)

江 维●

人教A版选修2-1第二章第一节练习第3题：已知点C的坐标是(2,2)，过点C的直线CA与x轴交于点A，过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点，求点M的轨迹方程.

教参中的解法如下：

解 设点A,M的坐标分别为(t,0)(x,y).

令x=0,得y=4-t，即点B的坐标为(0,4-t).

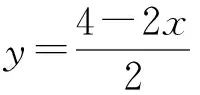
即x+y-2=0.①

(2)当t=2时，可得点A,B的坐标分别为(2,0),(0,2)，由此得点M的坐标为(1,1),它仍然适合方程①.

由(1)(2)可知，方程x+y-2=0是点M的轨迹方程，它表示一条直线.

视角一：参数法

题目中有三个动点，教参解法以点A的横坐标为参数，把点M的横纵坐标联系起来从而得到点M的轨迹方程.进而思考：点A,B,M的坐标都由直线CA的位置决定，不妨把M的横纵坐标用CA的斜率表示，再消去参数即得点M的轨迹方程.

消去k得x+y-2=0.

(2)当直线CA无斜率时，可得点A,B的坐标分别为(2,0),(0,2)，由此得点M的坐标为(1,1),它仍然适合方程x+y-2=0.

(3)当直线CA斜率为0时，可得点A,B的坐标分别为(0,2),(2,0)，由此得点M的坐标为(1,1),它仍然适合方程x+y-2=0.

综上所述，方程x+y-2=0是点M的轨迹方程，它表示一条直线.

视角二：相关点法

即然点M的坐标与点A,B有关，那么点A,B也可用点M的坐标表示，再由直线CA垂直于直线CB即可求出点M的轨迹方程.

即得点M的轨迹方程：x+y-2=0.

视角三：几何法

注意到∠BOA,∠BCA均为直角，所以A,C,B,O四点共圆，线段AB为直径，点M为圆心，所以MO=MC,则可迅速判断点M的轨迹.

解 (1)当直线不过原点时，∠BOA,∠BCA均为直角，所以A,C,B,O四点共圆.

又线段AB为直径，点M为圆心，所以MO=MC.

(2)当有一条直线过原点时，点M为一直角三角形斜边的中点，仍有MO=MC.

故点M的轨迹为线段OC的垂直平分线，其方程为x+y-2=0 .

我们可以看到，随着思维的深入，视角的变化，解题方法越来越简单.数学解题的思维具有方向性、灵活性与持续性，在求解的过程中，选择合适的视角，持续不断的思维，使问题在不同的角度得以解决，数学思维能力也将不断提高.

G632

B

1008-0333(2016)29-0050-01