深入研究真题，科学高效备考

山东省文登第一中学(264400)

崔 文● 侯宇虹●



深入研究真题，科学高效备考

山东省文登第一中学(264400)

崔 文● 侯宇虹●

高考复习需要有针对性，宽泛的复习效果差.对一道题目的研究要入木三分，发掘其内涵与外延，形成知识体系.结合实例，研究2013年山东高考文理22题，旨在提升利用高考真题搞好复习的效率.

压轴题；椭圆；斜率

高考22题为压轴题，因此22题的命题方向对高中数学教学导向作用明显，本文以2013年高考山东卷理科和文科的22题为例，结合教学实践，阐述一些看法.

理科22原题：

(Ⅰ)求椭圆C的方程；

(Ⅱ)点P是椭圆C上除长轴端点外的任一点，连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m，0)，求m的取值范围；

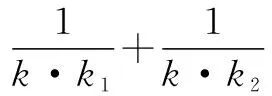
一、重视课本中典型例习题的发掘

人教B版《必修5》第5页例2：

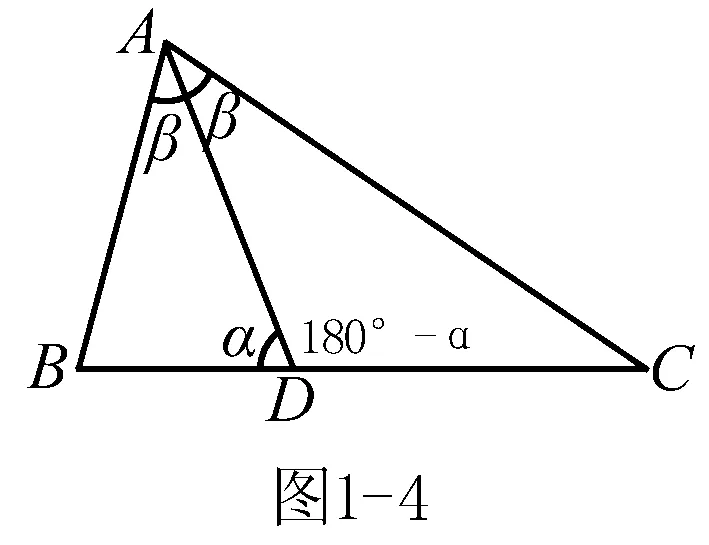
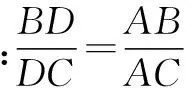
第9页习题1-1A第7题：

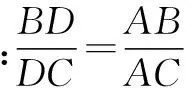
例2为“三角形的内角角平分线定理”，第7题为“三角形的外角角平分线定理”.这两个重要的定理在初中已经不作教学要求，高中阶段课程标准也没有要求记忆.但是，高考22题第(Ⅱ)问用三角形的内角角平分线定理解答十分简单.

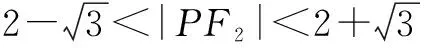
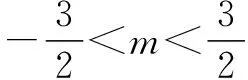
因此，对课本中典型的例习题需要有一定的熟悉度，掌握其证明方法.尤其是一些比较经典的知识，如上述的三角形内外角角平分线定理，笔者认为高中学生应该熟知.

二、重视教材教学内容的外延

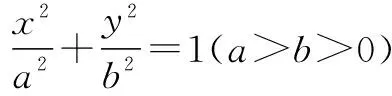
第(Ⅲ)问中“过点P作斜率为k的直线l，使得l与椭圆C有且只有一个公共点”，题目的背景大众化，我们常规的解法就是设出椭圆过点P的切线的方程，然后联立切线和椭圆的方程，判别式等于0即可得出斜率.

在日常教学中，用导数求函数在某一点处的切线的斜率已经非常熟悉，我们是否思考过用导数方法求过椭圆上一点的椭圆的切线的斜率？以及切线的斜率有无通用的表达式？

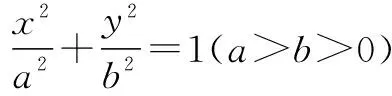
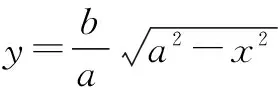
读者可以仿此方法研究双曲线和抛物线上一

▶

▶点P(x0,y0)处的切线斜率.可以查询资料如何用导数法(隐函数求导法则)求出圆锥曲线切线方程的斜率，因为不是高中数学课程标准规定学习内容，在此不叙述.

文科22原题：

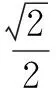
(Ⅰ)求椭圆C的方程；

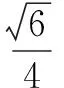
三、重视教材中的知识拓展性内容

人教B版教材有设置“探索与研究”、“思考与讨论”、“实习作业”等环节，授课对“思考与讨论”环节注重程度尚可，但是对教材上的其它环节一般理解为“冗余”，很少专门花时间进行研究.

文科的22题和理科的22题背景相似，也属于大众化的问题，但是在解法上需要精雕细琢.第(Ⅱ)问“ 的面积”通常的解法是首先求出弦长|AB|，然后求出点O到直线AB的距离，最后得出△AOB的面积.

可考虑用以下方法表示△AOB的面积.

解析AB斜率不存在时不再赘述.

当AB斜率存在时，设AB:y=kx+m(m≠0)，

代入椭圆方程得，(1+2k2)x2+4km+2(m2-1)=0，

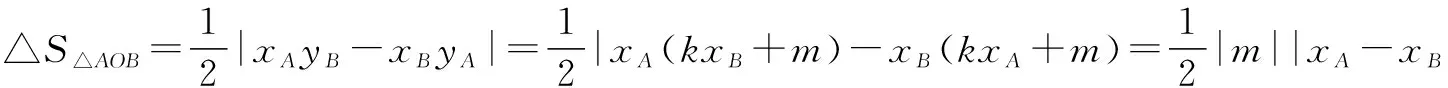
用此方法得到的△AOB的面积较之山东省招生考试院提供的参考答案运算简便许多.此公式在人教B版教材《必修5》第10页探索与研究《平行四边形与三角形的面积公式》一文内.

多角度研究试题，积累形成能力，才会突破高考中的新颖试题.考查什么？破题方法是什么？有无通法？对一道高考试题抽丝剥茧，方能运筹帷幄，决胜考场.

G632

B

1008-0333(2016)22-0011-02