H-P型有限单元法在L型钢模型优化设计中的应用

章 敏，张大卫，张建铭

(昆明理工大学 建筑工程学院, 云南 昆明 650500)



H-P型有限单元法在L型钢模型优化设计中的应用

章 敏，张大卫，张建铭

(昆明理工大学 建筑工程学院, 云南 昆明 650500)

提出了一种新的有限单元方法——H-P型有限单元方法，该方法主要是通过减小网格尺寸和提高插值多项式的阶数，在相对较少网格的前提下实现较高的计算精度，而且该方法在高阶计算时利用了低阶的计算结果，避免了重复计算，大大减少了计算工作量。重点介绍了该方法的理论基础，形状函数的构造，目前的主要研究成果，以及使用Stress Check软件对L型钢板模型进行数值模拟分析，所得的结果验证了所提算法的有效性。

h-p型有限单元方法；型函数；Stress Check；L型钢板；数值模拟

有限元法是工程计算和结构分析中应用最为广泛的数值计算方法。从解的结构上看，有限元法总体上可分为三种：h型有限元法，p型有限元法和h-p型有限元法。其中h-p型有限元法结合了h型有限元法和p型有限元法，即通过同时减少单元网格尺寸h(细分网格)和增加单元上插值多项式的阶数p来提高有限元解的精度。

1981年，Babuška[1]最先从理论上研究了p型有限元法，并证明了在拟一致网格上p型有限元法至少具有和h型有限元法一样的收敛速度，如果解具有rγ类型的奇性，则p型有限元法的收敛速度是h型有限元法收敛速度的两倍。Gui[2-4]从理论上系统地研究了一维h-p型有限元解的收敛性，并且给出了一维h-p型有限元解的误差估计。Babuška[5]也对h-p型有限元法进行了细致的研究，得到了h-p型有限元法的基本逼近结果。Babuška[6]对文献[1]的结果做了实质性的改进，并把二维p-型有限元法的结果推广到二维h-p型有限元法，为二维h-p型有限元法奠定了坚实的数学理论基础。

近三十年来，一维和二维的p型和h-p型有限元法取得了很多重要的进展，国内外的许多专家和学者取得了大量的研究成果。例如，除前面所提到的一些重要结果外，Demokowicz[7]较早地研究了一维的h-p型自适应有限元法；Szabó[8]进行了有限单元法分析；Guo[9]对R3空间中的h-p型有限元法的理论和算法进行了研究；Guo[10]研究了二维h-p型有限元法中的一类Schwarz方法；Schwab[11]分析了p和h-p型有限元方法；Sun[12]研究了二维h-p型有限元法的最佳收敛性，等等。

对于三维p型和h-p型有限元法，相应的研究成果尚不多见。文献[13]详细研究了三维空间中标准四面体单元上的多项式延拓算子，并将其成功地应用到三维h-p型有限元法中。Guo[14]研究了三维空间中标准五面体和六面体单元上的多项式延拓算子，并结合文献[13]得到的标准四面体单元上的多项式延拓算子结果，将其成功地应用到三维p型有限元法和h-p型有限元法中。2015年，Zhang[15]研究了拟一致网格上三维h-p型有限元法的收敛性。目前国内外对三维p型有限元法和h-p型有限元法的研究还在进行之中，p型有限元法和h-p型有限元法在工程计算中的应用还有待进一步深入研究。

1 H-P型有限单元解及形状函数的构造

假设S⊂U是有限维子空间，有限元法是根据变分公式

B(u，v)=f(v)，∀v∈S.

(1)

寻找有限元解uN∈S，并且满足

B(uN，v)=f(v)， ∀v∈S.

(2)

选择基函数φi(x)， 1≤i≤N 且

(3)

得到

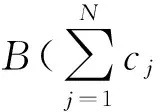
(4)

若B是双线性算子，则我们可得到

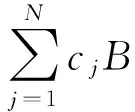
(5)

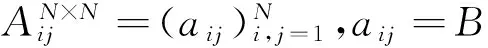
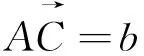
(6)

在有限元单元剖分时，如果定义hi为第i个单元Ωi的单元尺寸，即hi=diag(Ωi)，则若h=hi对所有i都成立，即所有单元尺寸都相同，则这样的网格剖分称为一致的网格剖分。若存在实数c1和c2，使得

(7)

那么随着网格的不断细分，hi变得越来越小，而实数c1和c2不变，则具有这种性质的网格称为拟一致的网格。本文主要讨论拟一致网格上的h-p型有限元法。

有限元空间S上的全局基函数是定义在毎一个单元Ωi上的分段连续函数拼接为定义在整个求解区域Ω上的连续函数。为了计算和编程时的快速、准确和高效，现代有限元法使用如下策略来构造基函数：

(1) 选择一个标准单元，也叫主单元，在标准单元上定义一系列标准函数Ni(ξ，η)，Ni(ξ，η)是关于变量ξ和η的阶数为pj的多项式，这种多项式被称为形状函数。

(2) 以二维情形为例，定义一系列映射Mk，Mk把标准单元S或T映射到第k个单元Ωk，1≤k≤K，Mk: x=Xk(ξ，η)， y=Yk(ξ，η)

(8)

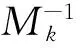
(9)

=Nj(Φk(x，y)，Ψk(x，y))

(10)

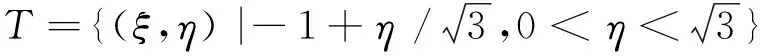
根据形状函数的构造，有两种不同类型的形状函数：拉格朗日插值类型的形状函数和阶谱类型的形状函数。

下面以二维情形为例，对标准正方形单元S和标准等边三角形单元T上的这两类形状函数的定义进行简要说明。

(A) 标准正方形单元S上拉格朗日插值类型的形状函数：

1. 标准正方形单元S上的双线性形状函数(每一变量的多项式阶数p=1)：

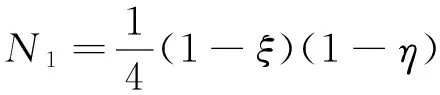
(11)

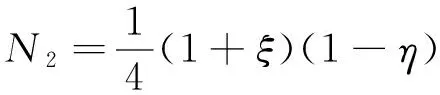
(12)

(13)

(14)

2. 标准正方形单元S上的双二次形状函数:

这里列举有限元计算分析软件中常用的两组形状函数。第一组形状函数包括以下8个函数：

(15)

(16)

(17)

(18)

(19)

(20)

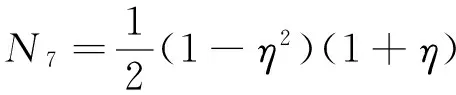
(21)

(22)

第二组形状函数包括9个函数，包括两种选择：

选择1：N1至N8与前面相同，只增加一个新的函数N9=(1-ξ2)(1-η2)使得

N9(P9)=1，N9(Pj)=0，1≤j≤8.

(23)

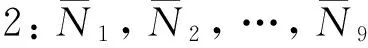
(24)

3. 标准等边三角形单元T上的线性形状函数:

(25)

(26)

(27)

式中，L1+L2+L3≡1。(L1，L2，L3)称为面积坐标，Li代表点(ξ，η)∈T到边Γi的距离。

4. 标准等边三角形单元T上的二次形状函数:

以Li表示有6个二次形状函数如下：

N1=L1(2L1-1)，

(28)

N2=L2(2L2-1)，

(29)

N3=L3(2L3-1)，

(30)

N4=4L1L2，

(31)

N5=4L2L3，

(32)

N6=4L3L1.

(33)

式中，每一个Ni都是阶数为2的多项式。

(B) 阶谱类型的形状函数：

标准正方形单元S上阶谱类型的形状函数：

a. p=1时节点模式

节点模式指的是与节点相关联的形状函数，节点模式是与拉格朗日插值类型一样的双线性函数：

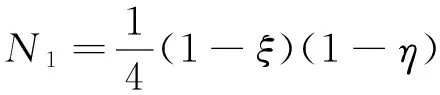
(34)

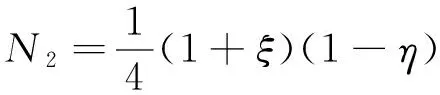
(35)

(36)

(37)

b. p≥2时边模式

边模式指的是与边相关联的形状函数，这里可以定义如下与边Γk(2≤k≤4)相关联的形状函数：

(38)

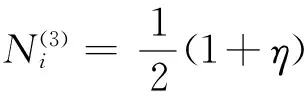
(39)

(40)

c. p≥4时内部模式

(41)

p=5时，增加两个内部模式形状函数

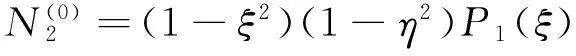
(42)

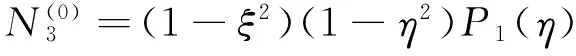
(43)

p=6时，增加三个内部模式形状函数

(44)

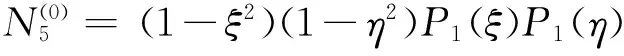
(45)

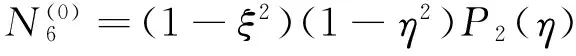
(46)

p=7时，增加四个内部模式形状函数

(47)

(48)

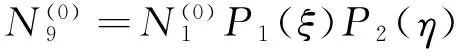
(49)

(50)

p=8时，增加五个内部模式形状函数

(51)

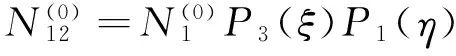
(52)

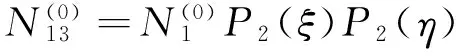
(53)

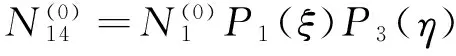
(54)

(55)

以此类推，当p>8时，我们可以增加新的内部模式形状函数，而且这些形状函数的顺序数关于多项式的阶数p是升阶谱的。

2 L数值算例

以h-p型有限元法作为理论和数值计算基础，采用基于h-p型有限元法的Stress Check有限元计算分析软件，分析并计算了L型钢板在受到侧面均布压力的荷载作用下，位移和应力的变化情况在受到水压力、淤沙压力、自重和场压力等基本组合荷载作用下的应力和位移。

2.1 相关参数

首先选取受侧面均布荷载压力的L型钢板进行数值模拟计算，L型钢板所用的材料类型为线弹性，具体参数如下：钢板长约5 m，弹性模量为200 GPa，泊松比为0.3，均匀分布的压力为1×106N/m2，除底部采用完全约束外，其他部位没有约束，图形实例如图1所示。

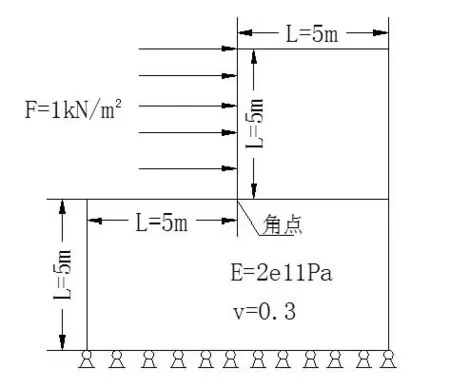
图1 L型钢板断面尺寸

2.2数值计算结果

基于h-p型使用有限元法计算分析软件Stress Check在不同网格划分情况下和在取不同插值多项式阶的情况下，计算和分析L型钢板在受到水平向右的均匀分布的压力的荷载作用下的应力大小和位移。

当网格数为588时，受侧面均布荷载1×106N /m2作用下L型钢板有限元计算模型的具体网格剖分、X方向最大位移Ux和角点处的第一主应力S1如图2和图3所示。

图2 X方向最大位移Ux

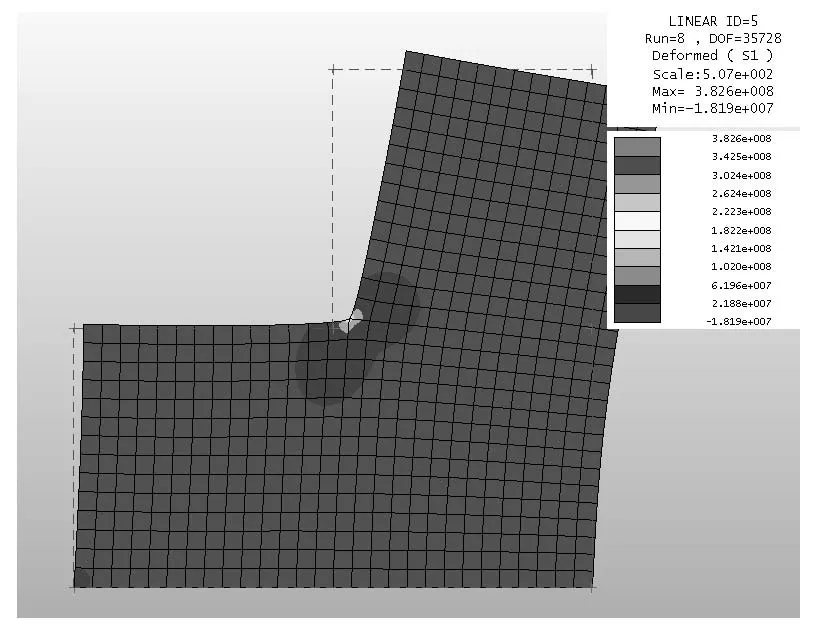
图3 角点处的第一主应力S1

通过计算我们分别得到单侧受压L型钢板在X方向最大位移Ux(单位：mm)、角点处的第一主应力S1(单位：Pa)和角点处的第一主应力S1的误差估计(%)(当P=1到8时)如表1所示。

当网格数为1728时，受侧面均布荷载1×106N /m2作用下L型钢板有限元计算模型的具体网格剖分、X方向最大位移Ux和角点处的第一主应力S1如图4和图5所示。

图5 角点处的第一主应力S1

通过计算，可得单侧受压L型钢板在X方向最大位移Ux、角点处的第一主应力S1和角点处的第一主应力S1的误差估计(%)(当P=1到8时)，结果见表2。

表1 X方向最大位移Ux和角点处的第一主应力S1计算结果

表2 X方向最大位移Ux和角点处的第一主应力S1计算结果

当网格数为2700时，受侧面均布荷载1×106N /m2作用下L型钢板有限元计算模型的具体网格剖分、X方向最大位移Ux和角点处的第一主应力S1如图6和图7所示。

通过计算我们分别得到单侧受压L型钢板在X方向最大位移Ux、角点处的第一主应力S1和角点处的第一主应力S1的误差估计(%)(当P=1到8时)如表3所示。

表3 X方向最大位移Ux和角点处的第一主应力S1计算结果

当网格数为3267时，受侧面均布荷载1×106N /m2作用下L型钢板有限元计算模型的具体网格剖分、X方向最大位移Ux和角点处的第一主应力S1如图8和图9所示。

通过计算我们分别得到单侧受压L型钢板在X方向最大位移Ux、角点处的第一主应力S1和角点处的第一主应力S1的误差估计(%)(当P=1到8时)如表4所示。

表4 X方向最大位移Ux和角点处的第一主应力S1计算结果

3 结束语

从以上计算结果可以看出，对于L型钢板在侧向受压的均布荷载时，使用Stress Check有限元计算分析软件在划分3267个网格数的时候，X方向最大位移Ux=2.791，角点处的第一主应力S1=4.419×8Pa，并且误差在可接受的范围内，说明h-p型有限元法通过同时减小网格尺寸和提高插值多项式的阶数而实现了较高的计算精度。同时从h-p型有限单元法的表上可以看出来，在P=1、P=2、P=3、P=4、P=5、P=6的情况下，应力增大的值是呈跳跃状的，说明h-p型有限单元法比h型有限元法具有网格划分少、收敛速度快、计算精度高和误差小的优点，并且保证结果的正确性和合理性，大大节省了我们的计算工作量。

[1] Babuška I, Szabó M, Katz N. The p-version of the finite element method [J].SIAM J. Numer. Anal., 1981，20：515-545.

[2] Gui W, Babuš ka I. The h, p and h-p versions of the finite element method in 1 dimension, Part 1. The error analysis of the p-version[J].Numer. Math., 1986，49：577-612.

[3] Gui W, Babuš ka I. The h, p and h-p versions of the finite element method in 1 dimension, Part Ⅱ. The error analysis of the h and h-p version[J].Numer. Math., 1986，49：613-657.

[4] Gui W , Babuš ka I . The h, p and h-p versions of the finite element method in 1 dimension, Part Ⅲ. The adaptive h-p version[J].Numer. Math., 1986，49：659-683.

[5] Babuš ka I, Guo B Q. The h-p version of the finite element method, Part 1 : The basic approximation results[J].Comp. Mech., 1986，1：22-41.

[6] Babuš ka I, Suri M. The h-p version of the finite element method with quasiuniform meshes[J].RAIRO Model Math. Anal. Numer., 1987，21：199-238.

[7] Demokowicz L, Oden T, Rachowicz W，et al. Towards a universal h-p adaptive finite element method, I. Constrained approximation and data structure[J].Comp. Meth. Appl. Mech. Engg., 1989，77：79-112.

[8] Szabó B, Babuš ka I . Finite element analysis[M].John Wiley and Sons, Inc, 1991：75-218.

[9] Guo B Q. The h-p version of the finite element method in R3: theory and algorithm[C]// Proceeding of ICOSAHOM 1995, 1995，56：487-500.

[10] Guo B Q, Cao W. An additive Schwarz method for the h-p version of the finite element method in two dimensions[J].SIAM J. Sci. Comput., 1997，18：1267-1288.

[11] Schwab C. p-and h-p finite element methods[M].Oxford Science Publication, 1998：124-256.

[12] Guo B Q, Sun W. The optimal convergence of the h-p version of the finite element method with quasi-uniform meshes[J].SIAM J. Numer. Anal., 2007，45：698-730.

[14] Guo B Q, Zhang J M. Stable and compatible polynomial extensions in three dimensions and applications to the p and h-p finite element method[J].SIAM J. Numer. Anal.，2009，47： 1195-1225.

[15] Zhang J M,He Y,Qi X.The convergence of the h-p version of the finite element method with quasi-uniform meshes in three dimensions[C]//AIP Conference Proceedings 2015, 15：222-338.

(责任编辑：熊文涛)

2016-03-02

国家自然科学基金项目(11261026)

章 敏(1987- )，男，安徽省安庆人，昆明理工大学建筑工程学院硕士研究生。

张大卫(1992- )，男，安徽省宿州人，昆明理工大学建筑工程学院硕士研究生。

O242.21

A

2095-4824(2016)06-0087-06

张建铭(1964- )，男，云南省昆明人，昆明理工大学建筑工程学院副教授，博士。