区间数多准则分类问题的一种UTADIS扩展方法

余胜平，熊文涛

(湖北工程学院 数学与统计学院， 湖北 孝感 432000)



区间数多准则分类问题的一种UTADIS扩展方法

余胜平，熊文涛

(湖北工程学院 数学与统计学院， 湖北 孝感 432000)

针对带有区间数的多准则分类问题，扩展了传统的UTADIS(UTilites Additives DIScriminantes)方法，提出了一种区间UTADIS(interval UTADIS，IUTADIS)方法。该方法不是将区间数转化为一个精确值(如均值)，而是根据区间数的端点，建立一个线性规划模型，得到了各方案的分配范围，即分类区间。由于是直接采用区间数的端点计算，所以可以尽量减少因区间数运算带来的信息损失；并且，决策人对部分方案的分配，只需提供分类区间，这样可使该方法更加灵活。最后，用一个算例说明了该方法的可行性。

UTADIS方法；区间数；加性效用函数；多准则分类问题

多准则分类问题是在多个准则下将有限个方案分配到事先定义的有序类中，这类问题在现实生活中十分常见，如信用评级[1]、安全软件的评估[2]、供应商的分类[3]，等等；文献中给出了大量的分类方法，并开发了一些软件[4-5]。在这些方法中，基于效用理论的方法是一类最普遍的方法，它将各方案在每一准则下的指标值转换成反映决策人偏好的效用值，然后利用某种融合方法将其综合成一个值，每个准则下的效用函数称为边际效用函数。边际效用函数的构造可分为直接方法和间接方法，前者需要决策者直接提供反映他/她偏好的具体值。后者则是从一组参考方案的分配实例中利用某种数学方法(如数学规划)推导计算出反映决策人偏好的参数值。由于间接方法计算模型一般比较简单，并且需要较少的认知，受到了许多学者的青睐。学者们提出了多种基于间接偏好信息的多准则分类方法，其中UTADIS方法[6]是一种典型的方法，它假设每一个准则下的边际效用函数都是分段线性函数，根据决策人提供的方案分类信息，利用加性方法构建一个线性规划模型，计算出每个方案的综合效用值。线性规划的约束条件使得计算结果与决策人提供的偏好信息尽可能一致，通过最小化决策人提供分配例子的分类误差，计算出每个方案的综合效用与类的阈值，将其分配给一个预定义的合适的类中。

然而，当决策人的案例分配相对较少时，数学规划模型可能有多个最优解，这意味着可以确定多个效用函数。在UTADIS方法中一般使用再优化分析检验排序结果的稳定性，得到最终的边际效用函数。另外，Greco et al[7]假设每个准则的边际效用函数仅是单调非降的函数，定义了必然偏好关系和可能偏好关系，提出了一系列多准则分类方法[8]。然而，这些方法都假设决策人提供的方案评价值和分类参数是精确的，不能有效处理带有不精确信息的问题。据笔者所知，只有少数文献处理了不精确数据的多准则分类问题，如文献[9]针对区间数多准则分类问题，扩展了Flowsort方法。本文则是对传统的UTADIS方法进行了一个简单、直观的扩展，假设各准则下的性能指标值均为区间数，且决策人提供部分方案的分配也是分类区间，即可能分配的最大类和最小类；结合文献[7]的思想，不是等分所有准则下的区间段，而是采用决策人提供的关键节点，计算其效用值，再利用分段线性插值，得到所有方案的分类区间。分类的结果用区间范围表示，增加了决策人的灵活性，且分类过程中没有因区间数的运算而丢失信息。

1 问题的描述

定义1[10]如果某个方案a分配的最好和最差类分别为CL(a)，CR(a)，则称[CL(a)，CR(a)]为方案a的分类区间，其中[CL(a)，CR(a)]表示一个连续CL(a)，CL(a)+1，…，CR(a)，L(a)≤R(a)，记为a→[CL(a)，CR(a)]。

显然，当且仅当L(a)=R(a)时，方案a的分配是精确分配。

2 带有区间数的UTADIS方法

这里考察方案在各准则下指标值均为区间数的决策情形，不是将区间数转换成像均值一样的精确数计算，而是直接利用区间数的端点计算。基于此，下面首先给出区间数的一些运算法则。

2.1 区间数的运算

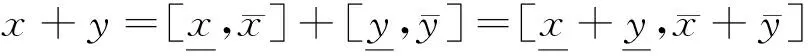
(1)

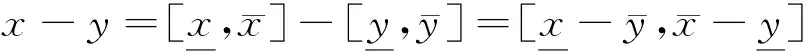
(2)

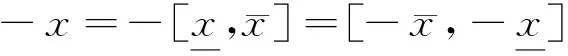
(3)

(4)

2.2 传统的UTADIS方法

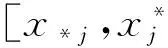
(5)

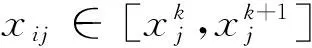
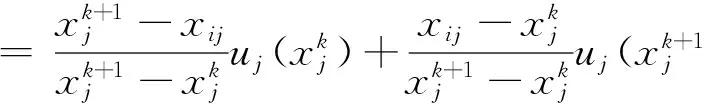
(6)

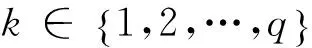
在与决策人提供的偏好信息尽量一致的前提下，UTADIS方法根据一个模型来估计综合效用值(加性效用函数)和效用阈值，这种模型本质上是一个目标规划模型。在决策人给出的决策案例中，可能存在低估误差σ-和高估误差σ+。以误差总和最小为目标函数，可构造线性规划模型I。

2.3 区间数多准则分类问题的参数推断模型

考虑到每个方案的指标值xij均为区间数，本文将模型I扩展为含有区间数的情形。根据公式(1)-(6)，利用区间数端点值计算出每个方案的最小综合效用值和最大综合效用值；再根据定义1，确定每个方案的分类区间。若决策人能提供的偏好信息为方案的分类区间，则模型I可扩展为模型II。

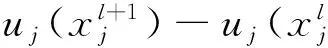
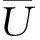
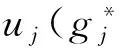
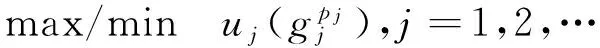
3 算例

考察如下的决策问题，假设有5个评估准则：g1：交货执行情况，g2：处理时间(天)，即需要开发产品结构设计的时间，g3：设计修改时间(天)，即需要执行项目的修改时间，g4：成型时间(天)，即需要构建原型的时间，g5：成本还原能力，其中g1、g5为效益型准则，g2、g3、g4为成本型准则。一家公司希望根据以往的经验将10个供应商a1，a2，…，a10分为4类：战略合作关系供应商(C1)、有前途的供应商(C2)、有竞争合作关系的供应商伙伴(C3)、需要取消合作的供应商(C4)，其中C1最好的类，C4为最差的类。由于实际中很难给出各个供应商的精确评估值和将部分供应商精确地归为某一类，这里假设这10个供应商在各准则下的评估值为区间数(见表1)，并且决策人根据以往的经验，可以给出部分供应商的分配范围(a1∈C2，即 a1→[C2，C2]，a2∈[C3，C4]，a3∈[C2，C3]，a4∈[C3，C4]，a5∈[C2，C3])，决策人给出各准则下关键节点见表2，试确定所有方案的分配范围。

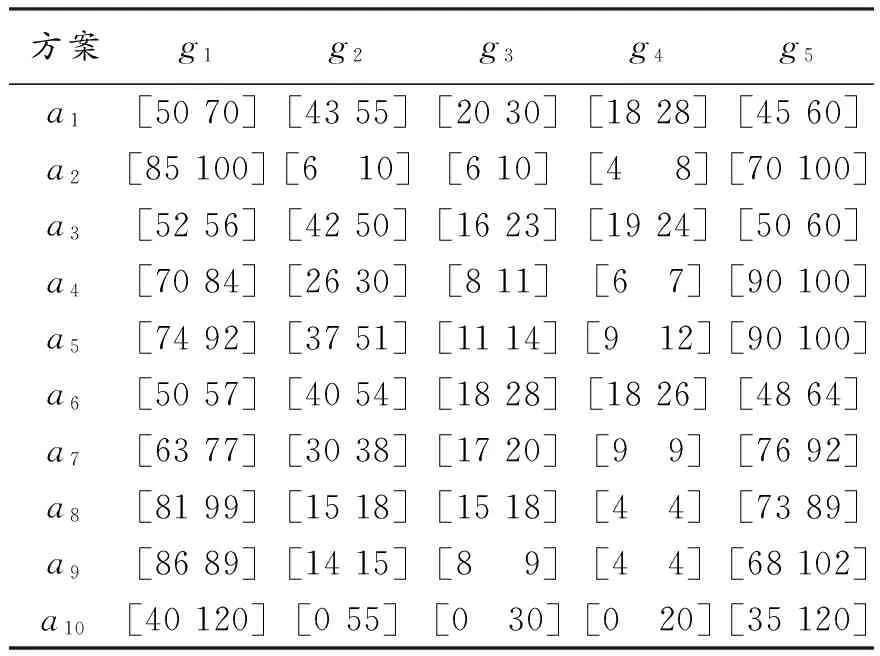
表1 10 个方案在5个准则下的评估区间数

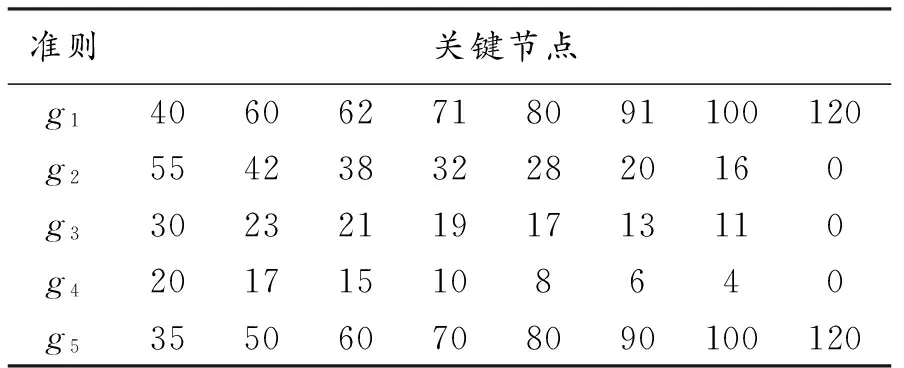
表2 各准则下的关键节点值

表3 各准则下的关键节点的效用值

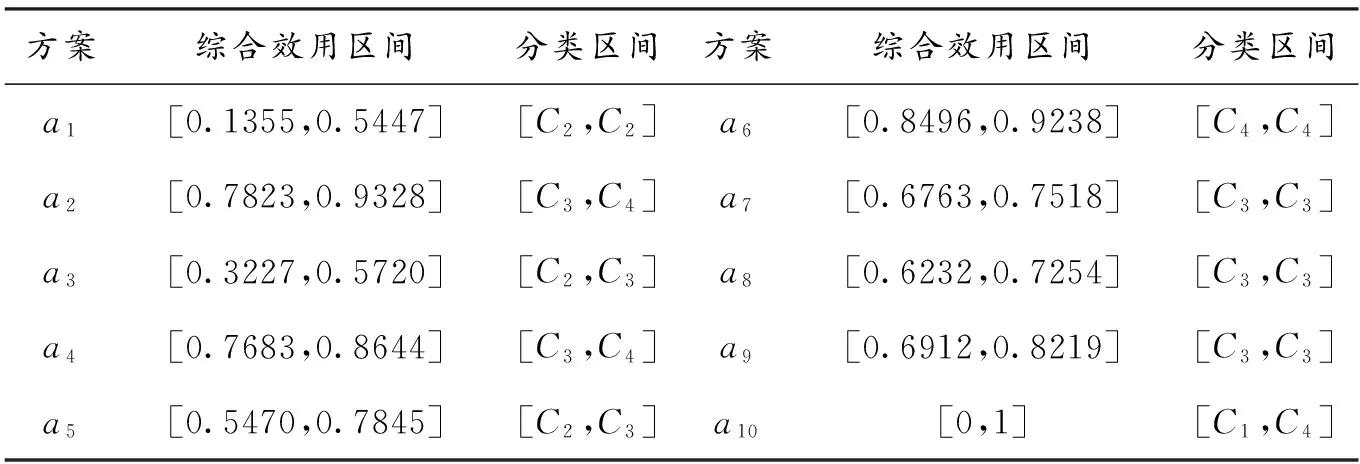
表4 所有方案的综合效用区间

从表4可知，方案a1，a2， …，a5和决策人提供的分类区间完全一致，说明本文提出的模型能在满足决策人提供偏好信息的前提下，对待评方案分类；由于决策信息为区间信息，所以结果一般为分类区间，但部分方案依然可精确分配，如a7，a9，而a10的分类最不确定，这可增加决策的灵活性。

4 小结

UTADIS方法是一种基于效用理论的多准则分类方法，本文对其进行了扩展，使之能处理评价值为区间数的多准则分类问题，并且降低了决策人提供案例的精确要求，只需要给出案例中方案的分配范围。根据本文给出的模型，最终可以得到每个方案分配的分类区间，以供决策人根据实际情况进一步决策，从而增加了决策的灵活性。

[1] Doumpos M, Zopounidis C. A multicriteria outranking modeling approach for credit rating[J].Decision Sciences. 2011, 42(3): 721-742.

[2] Lu G, Wang H, Mao X. Using ELECTRE TRI outranking method to evaluate trustworthy software[J].Autonomic and Trusted Computing. 2010: 219-227.

[3] Manshadi E D, Mehregan M R, Safari H. Supplier classification using UTADIS method based on performance criteria[J].International Journal of Academic Research in Business & Social Sciences. 2015, 5(2): 31-45.

[4] Zopounidis C, Doumpos M. PREFDIS: a multicriteria decision support system for sorting decision problems[J].Computers & Operations Research. 2000, 27(7): 779-797.

[5] Dias L C, Mousseau V. IRIS: A DSS for multiple criteria sorting problems[J].Journal of Multi-Criteria Decision Analysis.2003,12(4/5):285-298.

[6] Doumpos M, Zopounidis C. Developing sorting models using preference disaggregation analysis: An experimental investigation[J].European Journal of Operational Research. 2004, 154(3): 585-598.

[7] Greco S, Mousseau V, Sowiński R. Ordinal regression revisited: Multiple criteria ranking using a set of additive value functions[J].European Journal of Operational Research. 2008, 191(2): 416-436.

[8] Greco S, Kadziński M, Mousseau V, et al. Robust ordinal regression for multiple criteria group decision: UTAGMS-GROUP and UTADISGMS-GROUP[J].Decision support systems. 2012, 52(3): 549-561.

[9] Janssen P, Nemery P. An extension of the FlowSort sorting method to deal with imprecision[J].4or Quarterly Journal of the Belgian French & Italian Operations Research Societies. 2013, 2013(11): 171-193.

[10] Greco S, Mousseau V, Sowiński R. Multiple criteria sorting with a set of additive value functions[J].European Journal of Operational Research. 2010, 207(3): 1455-1470.

(责任编辑：邹礼平)

An Extension of UTADIS Method for the Multiple Criteria Sorting Problems with Interval Data

Yu Shengping, Xiong Wentao

(SchoolofMathematicsandStatistics,HubeiEngineeringUniversity,Xiaogan,Hubei432000,China)

We propose an extension of the traditional UTADIS sorting method for the multi-criteria sorting problems with interval data, which is called IUTADIS. In this method, the interval numbers are not reduced to crisp numbers, but calculated according to their endpoints. A linear programming model is established to obtain the ranges of categories that each alternative may be assigned, namely, the intervals of contiguous categories. Because the calculation is directly based on the endpoints of interval numbers, it can minimize the information loss because of interval computation. In addition, it is flexible because it only requires decision maker to offer the range of some alternatives. Finally, an example is given to illustrate the feasibility of the method.

UTADIS method; interval data; additive value function; multiple criteria sorting

2016-10-08

湖北省教育厅科学研究计划资助项目(Q20132706)

余胜平(1980- )，女，湖北襄阳人，湖北工程学院数学与统计学院讲师，硕士。

熊文涛(1978- )，男，湖北汉川人，湖北工程学院数学与统计学院副教授，博士。

C934

A

2095-4824(2016)06-0066-05