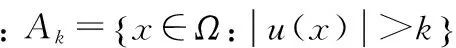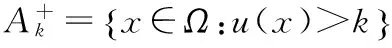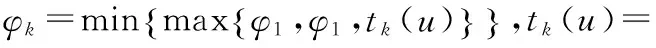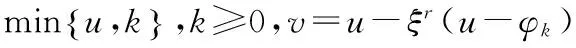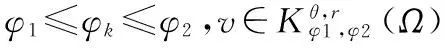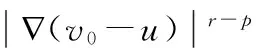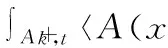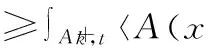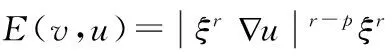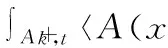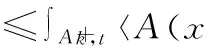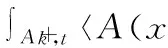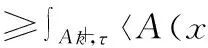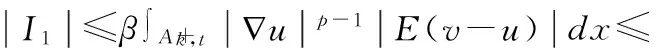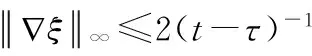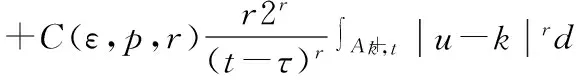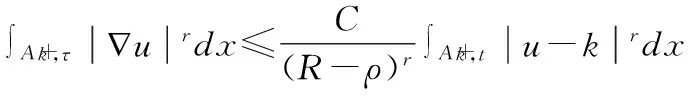非齐次椭圆型方程双侧障碍问题的很弱解

樊自安

(湖北工程学院 数学与统计学院，湖北 孝感 432000)



非齐次椭圆型方程双侧障碍问题的很弱解

樊自安

(湖北工程学院 数学与统计学院，湖北 孝感 432000)

运用Hodge分解方法,选择适当的检验函数,证明了一类非齐次椭圆型偏微分方程双侧障碍问题很弱解的局部有界性。

非齐次椭圆方程;很弱解;Hodge分解;双侧障碍问题

20世纪90年代, Iwaniec在文献[1-2]提出了很弱解的概念, 并用扰动向量场的Hodge分解研究了形如方程(1)的很弱解的性质，方程(1)称为A-调和方程。

-divA(x，u)=0

(1)

近年来， 运用Hodge分解法，已经取得了许多研究成果， 方程(1)障碍问题的弱解及很弱解也得到了广泛研究。文献[3]研究了方程(1)的障碍问题弱解的梯度更高可积性;文献[4]研究了方程(1)的障碍问题很弱解的局部有界性;关于方程(1)的障碍问题很弱解的性质的讨论还可见文献[5-6].类似于方程(1)的讨论方法，文献[10-12]研究了其他散度方程障碍问题的弱解及很弱解，其中文献[10]研究了非齐次A-调和方程(2)障碍问题的很弱解。

-divA(x，u)=f(x)

(2)

本文讨论方程(2)的双侧障碍问题的很弱解。

1 定义及预备知识

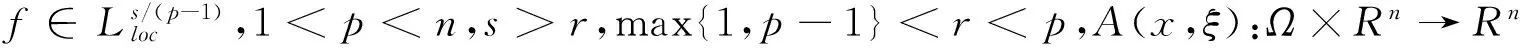
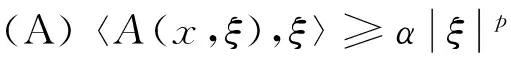
式中α，β>0是常数。

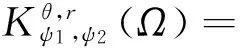
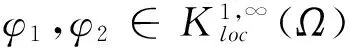
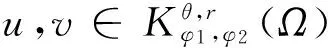
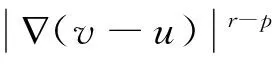
且有:

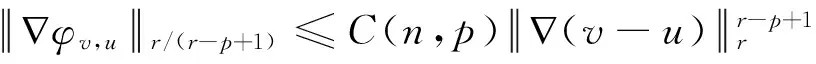
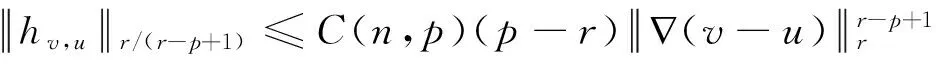
式中范数下标r表示Lr，以下不再说明。

下面给出方程(2)障碍问题很弱解的定义。

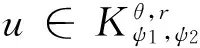
∫Ω〈A(x，(v-u)〉dx

≥∫Ω〈A(x，u)，hv，u〉dx+∫Ωfφv，udx .

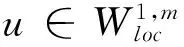
2 主要结果及证明

首先给出一个简单的引理， 后面定理的证明要用到这个结论。

引理1[7]设f(τ)是一个定义在0≤R0≤t≤R上的非负有界函数，且

f(τ)≤A(t-τ)-α+B+θf(t)

这里，A，B，α，θ是非负常数，θ<1.则存在常数c=c(α，θ)，对于任意ρ、R，当R0≤ρ

f(ρ)≤c[A(t-τ)-α+B]

引理2[8]假设一个函数u(x)属于B类，则对于BR⊂Ω，有

maxu(x)≤C.

下面给出方程(2)双侧障碍问题很弱解的局部有界性结果。

结论。

于是，由定义1得到

∫Ω〈A(x，(v0-u)〉dx≥∫Ω〈A(x，u)，hv，u，1〉dx+∫Ωfφv，u，1dx

由Hodge分解的唯一性及v0的定义得到当u>k，φv，u，1=φv，u，hv，u，1=hv，u;u≤k，φv，u，1=0，hv，u，1=0，于是

≥∫Ω〈A(x，u)，hv，u，1〉dx+∫Ωfφv，u，1dx

(3)

及

(4)

(5)

由(3)-(5)，得到

(6)

由条件(A)及(6)式，得到：

(7)

由条件(B)及(6)式，得到

式中ε>0。

(8)

现在来估计I2和I3。由Young不等式、条件(B)及Hodge分解得到

(9)

由(4)式

由Young不等式、Hodge分解得到

(10)

取ε和p-r足够小，使得0<ε0=C1ε+εβ+2C(ε，p)(p-r)β<1，取R1/2≤ρ

式中C=C(p，r，α，β)。

由引理1得到

由定义2，u(x)属于B类，因此由引理2，在R/2内，maxu(x)≤C，证毕。

[1] Iwaniec T, Sbordone C. Weak minima of variational integrals[J].J. Reine Angew. Math., 1994, 454: 143-161.

[2]IwaniecT,P-harmonictensorsandquasiegularmappings[J].Ann.Math., 1992, 136: 589-642.

[3]LiG,MartioO.Stabilityandhigherintegrabilityofderivativesofsolutionsindoubleobstacleproblems[J].J.Math.Anal.Appl.， 2002, 272:19-29.

[4]HongyaG,JinjingQ,YumingC.Localregularityandlocalboundednessresultsforveryweaksolutionsofobstacleproblems[J].JournalofInequalitiesandApplications, 2010(1): 1-12.

[5]LiG,MartioO.Uniquenessofsolutionswithveryweakboundaryvalues[J].NonlinearAnalysis:Theory,Methods&Applications, 2002, 51(4): 693-701.

[6]HongyaG,JingG,YaliZ,etal.Localregularityresultinobstacleproblems[J].ActaMathematicaScientia, 2010, 30(1): 208-214.

[7]Giaquinta,M.MultipleIntegralsintheCalculusofVariationsandNonlinearEllipticSystems[M].Princeton：PrincetonUniversityPress, 1983.

[8]Hong,MC.Someremarksontheminimizersofvariationalintegralswithnon-standardgrowthconditions[J].BollettinodellUnioneMatematicaItaliana,1992,6a(1):91-101.

[9]IwaniecT,MigliaccioL,NaniaL,etal.Integrabilityandremovabilityresultsforquasiregularmappingsinhighdimension[J].Math.Scand,1994,75(1):263-279.

[10] 周树清. 一类非齐次A-调和方程组很弱解的正则性[J].数学年刊A辑(中文版)，2002，23(3):283-288.

[11] 樊自安, 艾军, 胡付高. 一类散度形式椭圆型方程很弱解的唯一性[J].数学的实践与认识，2014,44(3):186-191.

[12] 李娟. 一类非齐次障碍问题的很弱解的局部可积性[J].山东大学学报(理学版)，2010,45(8):66-71.

(责任编辑：熊文涛)

2016-02-07

湖北省教育厅科学研究计划项目(B2015032)

O175.25

A

2095-4824(2016)03-0122-03

作者简介：樊自安(1972-), 男, 湖北广水人,湖北工程学院数学与统计学院副教授, 硕士。