蜂窝网格型球面网壳的非线性稳定性研究

贺拥军，彭正群

(湖南大学 土木工程学院，湖南 长沙 410082)



蜂窝网格型球面网壳的非线性稳定性研究

贺拥军†，彭正群

(湖南大学 土木工程学院，湖南 长沙 410082)

针对单层蜂窝网格型球面网壳利用有限元软件ANSYS对其进行了非线性稳定性研究.首先对两类蜂窝网格型球面网壳的稳定性能进行对比分析，确定了一种比较合理的网格布置形式.然后进行参数分析，分析了跨度、矢跨比、网格大小、初始缺陷、荷载不对称分布和材料非线性对网壳稳定性的影响.研究发现：在两类蜂窝网格形式的球面网壳中，网格Ⅰ型的整体稳定性能更好；分析建议其跨度不宜大于40 m，矢跨比取0.25左右，杆件长度取2 m左右，此时网壳整体稳定性较好，材料利用率较高；材料非线性对单层蜂窝网格型球面网壳的稳定承载力影响显著，考虑材料非线性后，网壳稳定承载力下降达50%；网壳对初始缺陷非常敏感，其理论最大缺陷值为跨度的1/150，此时网壳极限承载力最大下降达52%左右；网壳结构对荷载不对称分布不敏感.

单层蜂窝型球面网壳；稳定性；极限承载力；非线性分析

球面网壳是现代空间网壳结构应用非常广泛的一种结构形式，相对于双层球面网壳而言，单层球面网壳的总自由度约束大大减小，因而其刚度较弱，稳定性问题显得非常突出.近年来，国内外学者对三向网格型、肋环型、凯威特型等球面网壳的非线性稳定性的研究已比较成熟[1-5].

文献[6]建立了六边形网格球面网壳的参数化模型，但其杆件长度存在一定的差别，且不符合模数，不利于批量化生产.为解决此问题，本文从模型上做了大量的改进，使其杆件长度模数化：在球面坐标系下，采用等弧找点的办法(即利用已知点和弧长，再由结构对称性求得未知点)，在六分之一的对称扇形区域里从网壳的顶点开始逐个生成节点.通过这样的建模使得结构中的杆件长度(除与支座相连的杆件)完全相等，等长的杆件提高了工业化生产的效率，为施工也带来了极大的便利，同时形成了优美的六边形蜂窝网格结构，提高了观赏价值，具有很好的研究意义.

对于这种新型的网壳结构，其极限承载力主要是受结构的稳定性影响，所以本文深入地研究了此网壳结构的非线性稳定性.首先对比分析了不同网格形式对蜂窝型球面网壳稳定性的影响，确定了一种比较合理的网格布置形式，然后研究了矢跨比、杆件长度、初始缺陷、荷载不对称分布等因素对网壳稳定性的影响，并得出了网壳最优杆件长度区域.文章还重点分析了材料非线性对该网壳结构稳定性的影响，利用大型有限元软件ANSYS进行了800余例非线性全过程分析，比较真实地反映了此类结构的稳定性能，以期能为该结构形式的应用提供理论指导.

1 结构分析模型

根据结构杆件的布置形式不同，单层蜂窝网格型球面网壳组成了两类网格形式：蜂窝网格Ⅰ型球面网壳顶点位于六边形网格的中心点，蜂窝网格Ⅱ型球面网壳顶点处于3个空间六边形节点交汇处.在球面坐标系下，首先生成对称轴上的网壳节点，然后在局部坐标系下，依次生成扇形区域的各个节点，最后旋转生成结构模型，如图1所示(图中侧视图为主要研究对象-网格Ⅰ型).

本文模型钢材选用Q235，屈服强度为235 MPa，弹性模量取为2.1×105MPa,密度取7 800 kg/m3.材料选用双线性折线模型，切线模量为2.1×102MPa，遵从von Mises屈服准则.分析中结构杆件均采用BEAM188梁单元，网壳中杆件均采用圆钢管，无特别说明截面尺寸均为Ф146×5，网壳节点假定为刚接，支座设定为固定铰支座.

2 蜂窝型网壳稳定性能对比分析

为研究不同网格形式对蜂窝型球面网壳稳定性的影响，本节对两类蜂窝型球面网壳进行全过程跟踪分析，得到网壳的荷载-位移全过程曲线[7-8]，比较分析它们的极限承载力和刚度的差异.

选取结构矢跨比0.25，跨度分别选取24 m，27 m，30 m，33 m，36 m，网壳承受竖向均布荷载，对上述两类蜂窝型球面网壳进行极限分析，得出对应的极限荷载(见表1)．图2给出了跨度为30 m的两类网壳的荷载-位移全过程曲线，位移节点选取迭代结束时竖向位移最大的节点.

从图2可以看出，蜂窝型球面网壳网格Ⅰ型和网格Ⅱ型的极值点十分接近，且两条曲线的上升段几乎重合，说明了两类网格结构丧失稳定时的极限承载力相近，在弹性阶段结构的整体刚度也相差不大，但是在网格Ⅱ型发生极值点失稳破坏之后，网格Ⅰ型位移还在不断增加，还能继续承载，说明网格Ⅰ型具有更好的延性.

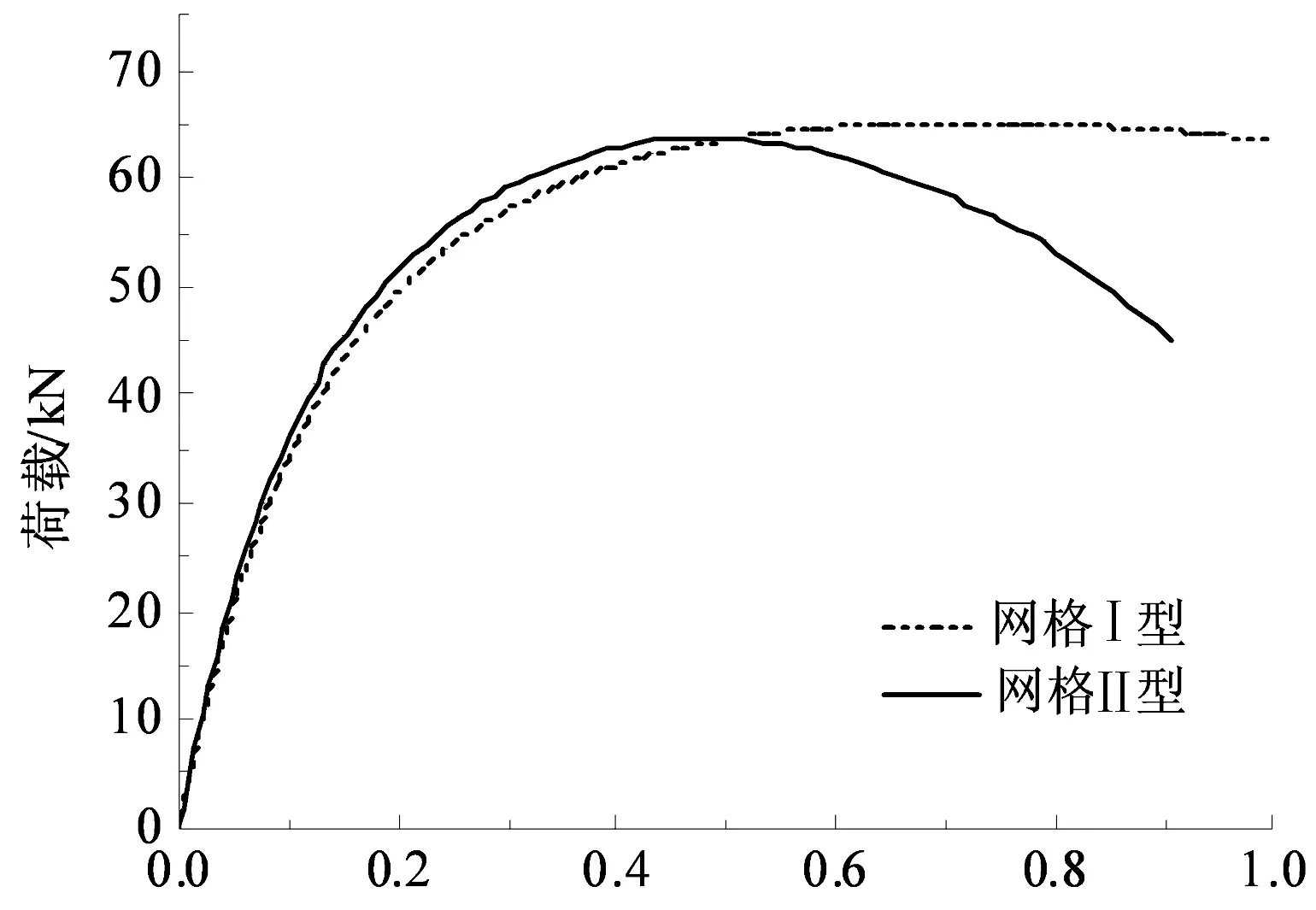
位移/m图2 两类蜂窝型球面网壳荷载-位移全过程曲线对比Fig.2 Comparison of complete load-deflection curve between two kinds of honeycomb spherical reticulated shells表1 两类蜂窝型球面网壳极限分析结果Tab.1 Ultimate analysis results of two types of honeycomb spherical reticulated shells kN

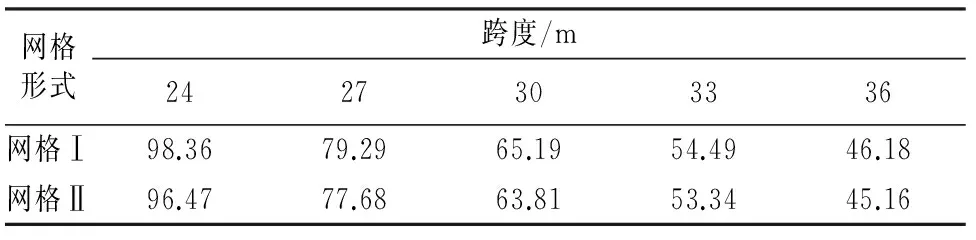
由表1可以看出，网壳基本结构体系模型Ⅰ和模型Ⅱ的极限荷载值随跨度的增加而逐渐减小，这表明其整体稳定性随跨度的增加而递减.在相同跨度和矢跨比的情况下，两种网格形式的蜂窝型球面网壳极限荷载相差不大，最大相差也在5%以内.

综上所述，对比两类蜂窝型球面网壳之后发现：它们的极限承载力区别不大，但延性差别明显，网格Ⅰ型比网格Ⅱ型具有更好的延性.所以下文将围绕网格Ⅰ型球面网壳进行分析，研究不同几何参数和非线性对该网壳稳定性的影响.

3 几何参数分析

3.1 矢跨比对网壳稳定性的影响

本节主要分析矢跨比对单层蜂窝型球面网壳极限承载力的影响规律，采用了24 m，27 m，30 m 3种跨度，每种跨度选用矢跨比0.15，0.20，0.25，0.30，0.35，0.40，杆件截面选取Ф146×5.由于矢跨比的改变，杆件长度也发生变化，网壳用钢量也随之改变，为了综合考虑极限荷载与用钢量两个因素，故用每吨钢筋所承受的荷载P来表示极限荷载的变化情况，其结果如图3所示.

从图3可以看出，各曲线斜率在逐渐减小，在相同跨度下，所有结构的极限荷载随矢跨比的增加出现了先增加后又逐渐减小的趋势.同时可以发现，跨度和矢跨比对单层蜂窝型球面网壳极限承载力都具有较大影响，其中跨度的影响更为显著.图中显示矢跨比为0.25时，单位用钢量的极限承载力都达到了最大值.进一步分析发现，主要是由于矢跨比的增加造成杆件长度变长，网格变大，导致承载力降低，由此说明蜂窝网格型球面网壳的极限承载能力受网格稀疏程度的影响较大.所以在实际工程设计中，在考虑网壳稳定性和材料利用率的因素下，建议矢跨比取0.25左右.

矢跨比f/s图3 极限荷载与矢跨比关系Fig.3 Relationship between ultimate loads and raise-span ratios

3.2 跨度对网壳稳定性的影响

为了探索单层蜂窝网格型球面网壳适宜的跨度，本节针对7种不同的跨度(L=21 m,24 m,27 m,30 m,40 m,50 m,60 m)，取结构矢跨比为0.25，杆件长度取为2 m，分别选取4种杆件截面(如图4所示).结构承受竖向均布节点荷载，分别进行几何非线性极限分析，同样在图4中用单位用钢量下的极限荷载P作为纵坐标，计算结果如图4所示.

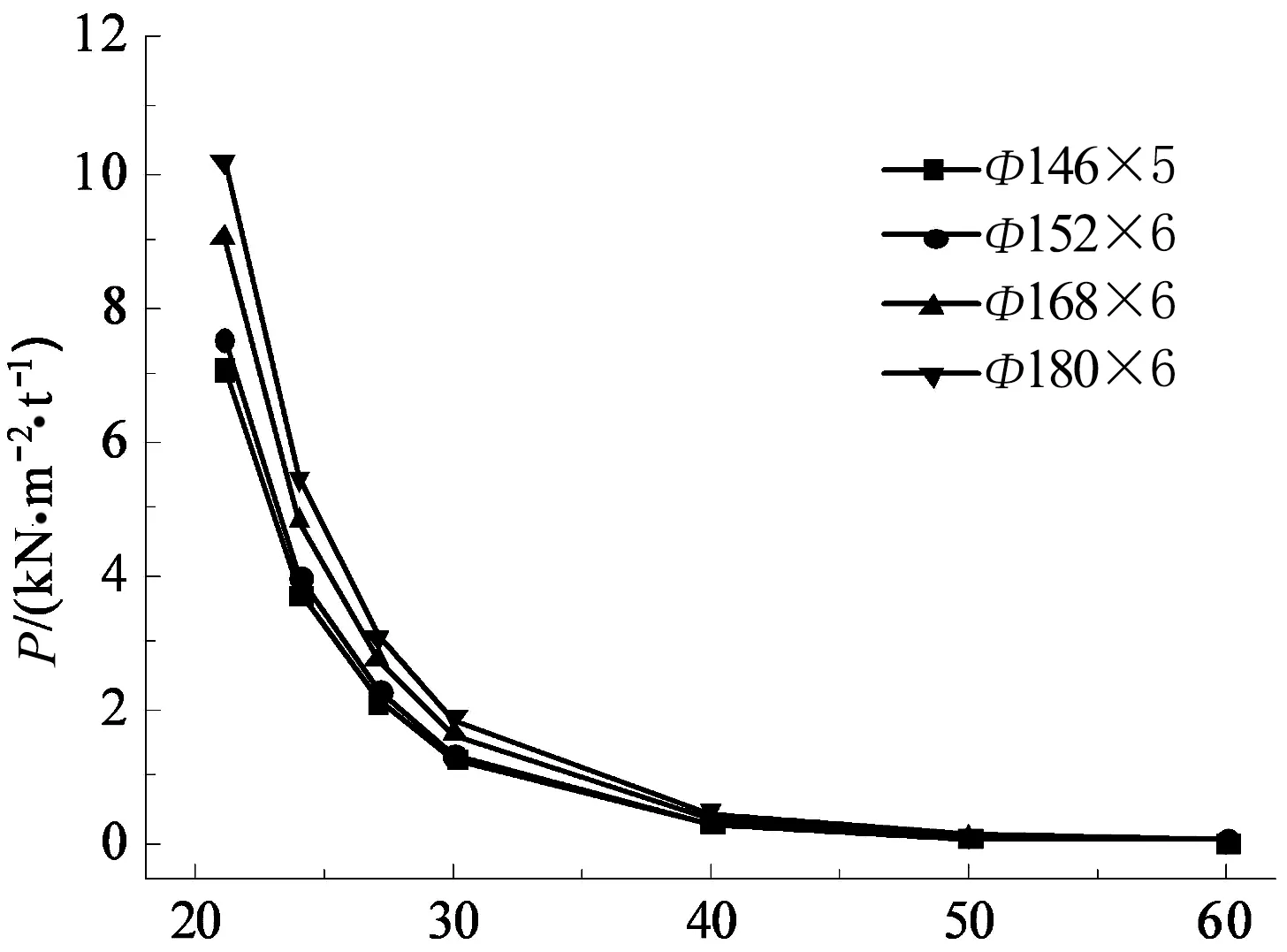
跨度/m图4 限荷载与跨度关系Fig.4 Relationship between ultimate loads and the span

从图4中可以看出，在相同杆件截面下，跨度较小时，单位用钢量下的极限荷载随着跨度的增大发生较大的降低;当跨度进一步增大，极限荷载的降低幅度逐渐减弱;在跨度大于40 m后，单位用钢量下的极限荷载变化趋于稳定，增大杆件截面再也无法提高P值大小，即与杆件截面的变化无关.由于在跨度大于40 m后，单位用钢量下的极限荷载值已经很小，且增大杆件截面也无法提高P值的大小.由以上分析可以得出结论：为保证单层蜂窝网格型球面网壳具有较大承载力与较好的材料利用率，其跨度不宜过大，建议跨度不要大于40 m.

3.3 网格大小对网壳稳定性的影响

《规程》中对于网格尺寸没有具体规定，大都是根据国内外实践经验来取值[9].本文研究的蜂窝型球面网壳的稳定承载力受网格尺寸影响很大，现用杆件长度的不同来代替网格疏密程度的不同.本节选取3种跨度24 m，27 m，30 m，矢跨比取为0.25，在矢跨比相同时，分别建立杆件长度为1.0 m，1.5 m，2.0 m，2.5 m，3.0 m共15个模型，杆件截面规格为Ф146×5和Ф152×6分别用下标1和2表示，非线性极限分析结果如表2所示.其中λ为平均应力系数，计算公式为：

式中：n为网壳结构的杆件数量；σi代表某杆件的应力值；f为杆件的强度设计值.

平均应力系数的大小其实可以作为评定材料利用率的一个标准，只有越多的杆件达到其材料的强度设计值，此时的平均应力系数就会越接近于0.

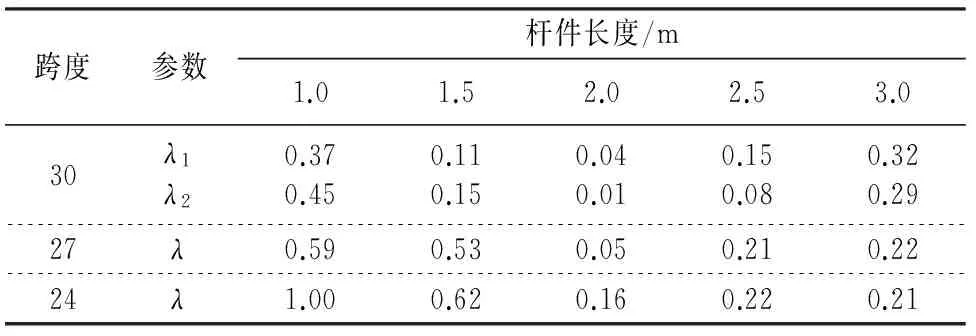
表2 不同杆件长度结构极限分析对比Tab.2 Comparison of ultimate analysis of the structure with different length of bar

从表2中可以看出，在不同跨度的网壳中，平均应力系数随杆件长度的增加基本上都出现了先减小后又增大的现象，而当杆件长度为2 m左右时，平均应力系数最接近于0，说明此时网壳结构的材料利用率最大.进一步研究发现，当杆件长度大于等于2.5 m时，大部分的杆件应力都未达到其强度设计值，网壳提前发生失稳破坏，此时材料没有得到充分发挥，材料利用率较低.而当杆件长度小于等于1.5 m时，很多杆件应力均超过了材料强度设计值，说明网壳设计主要由强度条件决定.又由于杆件截面对网壳稳定承载力影响显著，所以选取了不同截面进行了对比分析.表中30 m跨度的两种截面的应力影响因子很接近，其变化规律基本相同，说明不同杆件截面对其影响可以忽略不计.

综上所述，为保证网壳良好的整体稳定性和充分提高材料的利用率，建议蜂窝型球面网壳结构的杆件长度取值在2 m左右为宜.

4 初始几何缺陷的影响

先前计算过程中未考虑初始缺陷的影响，所以得到的极限承载能力往往会偏高.而实际工程中很难避免初始缺陷的影响[10-12].本节选取跨度为30 m，矢跨比为0.25，杆件长度取2 m，杆件截面选取Ф146×5，并对所研究的网壳取9种不同的初始缺陷(r=0 cm，2 cm，4 cm，6 cm，8 cm，10 cm，20 cm，30 cm，40 cm)进行分析.图5为网壳弹性极限荷载随初始缺陷值变化的荷载-位移全过程曲线，且对比分析了弹性和弹塑性临界荷载随初始缺陷变化的规律.

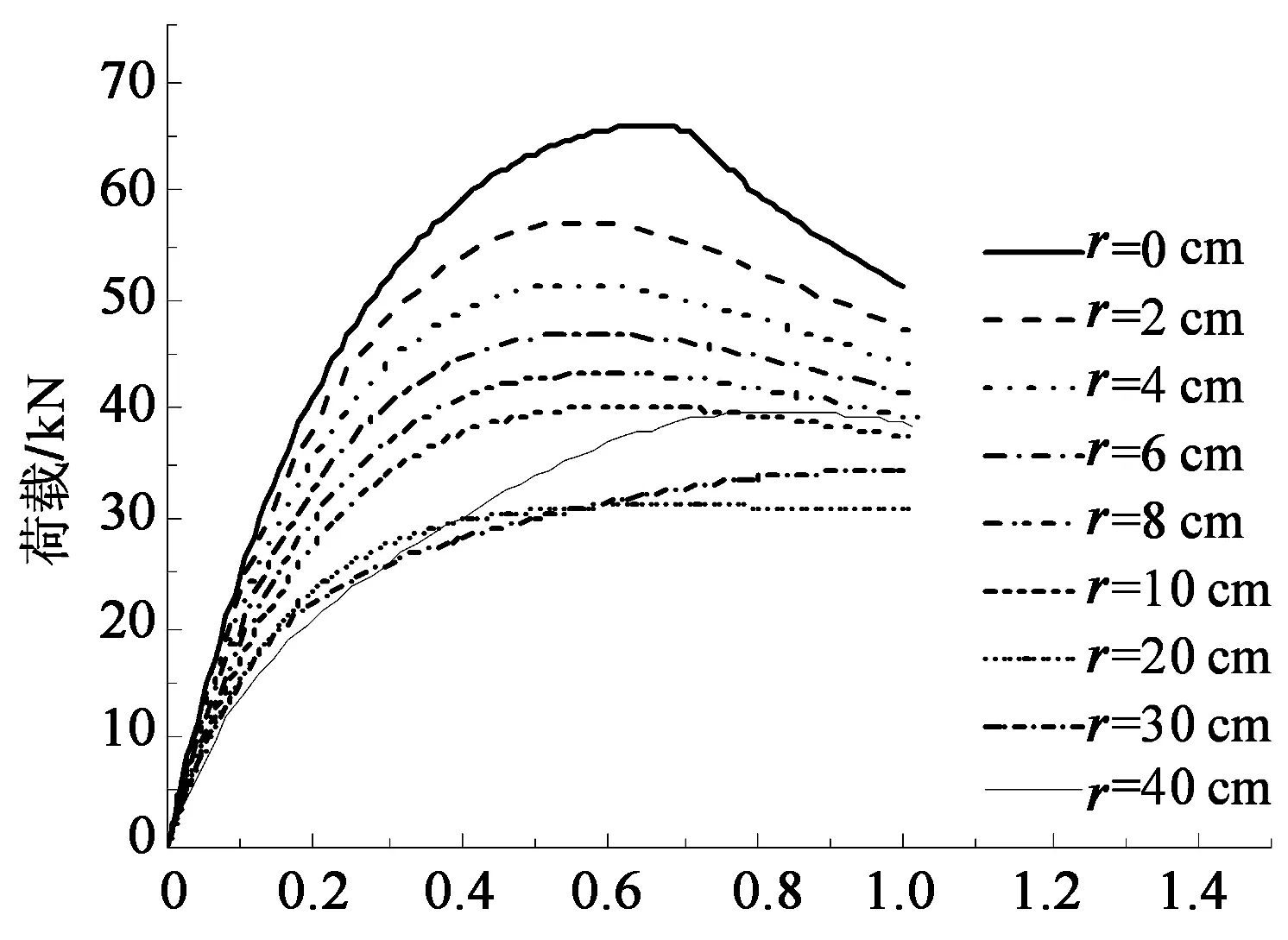
位移/m (a) 不同缺陷值的全过程曲线

缺陷值/m (b) 临界荷载与缺陷值的变化关系曲线图5 不同缺陷值的全过程曲线 及临界荷载变化曲线Fig.5 Complete load-deflection curve and critical load curve of domes with different initial imperfections

从图5可以看出，单层蜂窝型球面网壳由于受到初始缺陷的影响，其极限承载力不断的下降.另外，在网壳达到极限承载力之前曲线的斜率也随着缺陷的增大而逐渐的下降，表明网壳的整体刚度随着初始缺陷的增加而不断减小.作为对比，图中还描绘了弹塑性临界荷载的变化趋势，在缺陷值小于0.2 m时，单层蜂窝型球面网壳对于初始缺陷比较敏感，特别是在初始几何缺陷较小的时候，曲线的曲率较大，极限荷载下降较快，随后弹塑性网壳临界荷载曲线逐渐趋于平稳；但当缺陷值达到0.2 m时，弹性网壳曲线出现了最低点，之后承载力随缺陷值的增加反而增加，即说明网壳出现了“畸变”，已失去了研究意义.

由以上分析可以看出，单层蜂窝型球面网壳对初始缺陷非常敏感，其理论最大初始缺陷值可按跨度的1/150取值，但是实际工程安装过程中的节点位移偏差通常不会大于跨度的1/300，为偏于安全考虑，建议其实际网壳的极限承载力取理想网壳极限承载力的50%左右.

5 材料非线性的影响

考虑材料非线性后会直接影响到网壳的稳定性能，同时也会使得网壳极限承载力显著降低.本节在3.3节的基础上增加了两种跨度33 m,36 m，同时增加了两种截面Ф168×6，Ф180×6，每一例网壳结构分别考虑4种不同的缺陷值(图中用r表示缺陷,L表示杆件长度).所有网壳结构都分别进行了弹性分析和弹塑性分析，共计800个数据，这样可以更客观地知道考虑材料非线性后网壳极限承载力的下降比率，本节用ζ(弹塑性极限荷载puep和弹性极限荷载pue的比值)表示材料非线性折减系数：

ζ=puep/pue

计算结果用散点图表示如图6所示：

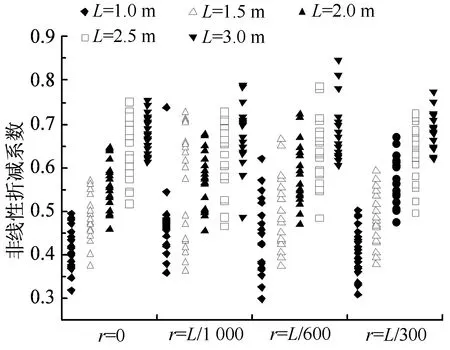
缺陷值图6 蜂窝型球面网壳材料非线性折减系数Fig.6 The relative curve between the limit loads and the initial imperfections

分析结果可知，当初始缺陷为0时，材料非线性折减系数ζ的平均值为0.553；初始缺陷为L/1 000时，ζ的平均值为0.557；初始缺陷为L/600时，ζ的平均值为0.572；初始缺陷为L/300时，ζ的平均值为0.577．由此可见随着缺陷的增加，材料非线性对网壳极限荷载的影响也在缓慢降低，但最大与最小值的差值都未超过5%，所以可以认为ζ的值受初始缺陷值的影响很小.为进一步研究杆件长度对ζ值的影响规律，在统计计算中以95%的保证率为标准，可分别求得不同杆件长度下的非线性折减系数(如图7所示).从图中可以看出ζ的值随杆件长度增长而逐渐增大，随截面的减小而增大，同时可以看出杆件长度相比截面而言，对ζ的值影响更大.表明网格越稀疏，结构的整体刚度越小时，材料非线性对网壳的极限承载力的影响就越小.

杆件长度/m图7 材料非线性折减系数Fig.7 Reduced coefficient of material nonlinearity

通过对材料非线性折减系数的统计可得出，蜂窝网格型球面网壳弹塑性稳定承载力与弹性网壳相比平均降低约为50%.由此说明网壳稳定性设计中需要考虑材料非线性的影响.

6 荷载不对称分布的影响

《规程》中球面网壳的全过程分析可按满跨均布荷载进行，对单层蜂窝型球面网壳由于其结构的特殊性，本节对每例网壳按图8所示3种不同的活荷载布置，提出5种竖向荷载比例(p/g=0,0.25,0.5，0.75,1，p为竖向均布活荷载，g为竖向均布恒荷载)，并对网壳进行双重非线性分析.图9给出了完善网壳(实心点)和缺陷网壳 (空心点，r=L/300)结构极限荷载随不同活荷载分布的变化曲线.

图8 考虑不同活荷载分布形式Fig.8 Considering different live load distribution form

由图9可以发现，理想网壳结构的极限承载力随活荷载比值的增大出现先增大后减小的现象，其中不对称荷载分布Ⅱ影响较突出，网壳结构的极限荷载最大下降率达到了8%左右.而对于带有初始缺陷的网壳结构，其极限承载力随活荷载比值的增大出现了逐渐增加的趋势，即增加活荷载比例对网壳结构的极限承载力提高有利，在实际网壳设计中不考虑它对网壳的有利作用，可以把它作为一定的安全储备.

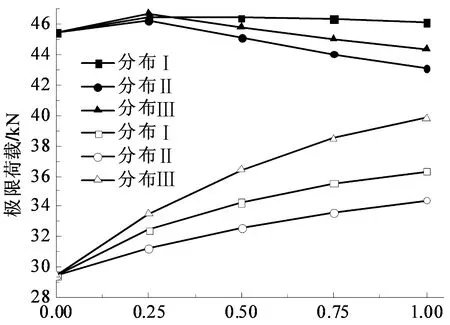
p/g图9 极限荷载随竖向荷载不对称分布变化曲线Fig.9 Curves of ultimate loads under unsymmetrical

由以上分析可知，对于单层蜂窝型球面网壳结构来说，其极限承载力的大小对活荷载分布不是很敏感，所以对该类网壳进行极限分析时可不考虑荷载不对称分布的影响.

7 结 论

根据以上研究，可得到如下主要结论：

1) 两类蜂窝型球面网壳结构极限承载力区别不大，但网格Ⅰ型具有更好的延性.

2) 矢跨比对单层蜂窝型球面网壳结构的稳定性影响显著且具有良好规律性，考虑网壳稳定性和材料利用率的因素，建议矢跨比在0.25左右.

3) 结构的跨度不宜大于40 m.

4) 网格大小对结构的影响较大，存在较优的杆件长度使得蜂窝型球面网壳具有较高的承载力和整体材料利用率，建议杆件长度取2 m左右.

5) 结构对初始缺陷敏感，最大缺陷值达跨度的1/150时，其网壳实际的极限承载力可取理想网壳极限承载力的50%左右.

6) 材料非线性对网壳极限承载力的影响非常突出，所以在实际工程中在对该网壳进行设计分析时，应考虑材料非线性的影响.

7) 竖向不对称荷载作用对网壳影响不大.

[1] 贺拥军, 周绪红, 刘旦.单层倒悬链型柱面网壳的非线性稳定性研究[J].湖南大学学报:自然科学版, 2012, 39(6):1-6.

HE Yong-jun, ZHOU Xun-hong, LIU Dan. Nonlinear buckling of inverted catenaty single-layer cylindrical reticulated shells [J]. Journal of Hunan University:Natural Sciences, 2012, 39(6):1-6. (In Chinese)

[2] HOANG Chi Tran, JAEHONG Lee. Geometric and material nonlinear analysis of tensegrity structures [J]. Actamechanica Sinica, 2011, 27(6): 938-949.

[3] 曹正罡, 范峰, 沈世钊.单层球面网壳的弹塑性稳定性 [J].土木工程学报, 2006, 39(10):6-10.

CAO Zheng-gang, FAN Feng, SHEN Shi-zhao. Elasto-plastic stability of sing-layer reticulated domes [J]. China Civil Engineering Journal，2006, 39(10):6-10. (In Chinese)

[4] 姜正荣, 魏德敏，张科龙,等.某大跨单层球面网壳结构的非线性屈曲研究 [J].空间结构, 2014, 20(1):40-45.

JIANG Zheng-rong, WEI De-min,ZHANG Ke-long,etal. Research of non linear buckling for one large-span single-layer spherical latticed shell [J]. Spatial Structures, 2014, 20(1): 40-45. (In Chinese)

[5] 郭远翔, 黄慧隆. 大跨度单层混合型球面网壳非线性稳定性研究 [J]. 结构工程师, 2014, 30(1): 58-62.

GUO Yuan-xiang, HUANG Hui-long. Nonlinear stability analysis of a large-span single-layer mixer spherical reticulated shell structure [J]. Structural Engineers,2014, 30(1):58-62. (In Chinese)

[6] 葛志龙, 鹿晓阳,王巧莎.蜂窝型球面网壳参数化设计 [J].钢结构, 2014,29(5):37-39.

GE Zhi-long, LU Xiao-yang, WANG Qiao-sha. Parametric design of honeycomb spherical latticed shell [J]. Steel Construction，2014, 29(5):37-39. (In Chinese)

[7] 董石麟, 郑晓清, 白光波.六杆四面体单元组成的新型球面网壳的稳定性能分析[J].空间结构, 2014, 20(4):29-38.

DONG Shi-lin, ZHENG Xiao-qing, BAI Guang-bo. StabilIty analysis of a novel spherical lattice shell composed of six-bar tetrahedral units [J].Spatial Structures, 2114, 20 (4):29-38. (In Chinese)

[8] 贺拥军, 周绪红, 董石麟. 单层叉筒网壳静力与稳定性研究 [J].湖南大学学报:自然科学版, 2004, 31(4):45-50.

HE Yong-jun, ZHOU Xu-hong, DONG Shi-lin. Research on static and stability properties of single layer latticed intersected cylindrical shell [J]. Journal of Hunan University:Natural Sciences, 2004, 31(4):45-50. (In Chinese)

[9] JGJ 7-2010空间网格结构技术规程[S]. 北京：中国建筑工业出版社， 2010: 19-20.

JGJ 7-2010 Technical specification for latticed [S]. Beijing: China Architecture and Building Press, 2010:19-20. (In Chinese)

[10] YAMADA S, TAKEUCHI A, TADA Y,etal. Imperfection sensitive overall bucking of single-layer latticed domes [J]. Journal of Engineering Mechanics, 2001, 4: 382-386.

[11]KATO S, YAMAUCHI Y, UEKI T. Buckling load of elliptic paraboloidal single layer reticulated roofs under uniform load [J]. International Journal of Space Structures, 2005, 20(2): 91-106.

[12]SCHENK C A, SCHUELLER G I． Buckling analysis of cylindrical shells with random geometric imperfections[J]. International Journal of Nonlinear Mechanics，2003, 38: 1119-1132.

Nonlinear Stability Analysis of Single-layer Honeycomb Spherical Latticed Shells

HE Yong-jun†，PENG Zheng-qun

( College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China)

The finite element software ANSYS was used to investigate the nonlinear stability of single-layer spherical latticed shells with hexagonal connection form. Firstly, a reasonable grid layout was determined by analyzing and comparing the stability of two types of honeycomb spherical latticed shells. A large scale parametric analysis was then carried out, including the influences of the span, raise-span ratios, grid size, initial geometric imperfection, asymmetric load distribution, and material nonlinearity on the stability behavior of honeycomb spherical latticed shells. The results show that the grid of typeⅠexhibits better overall stability capacity for two kinds of grid configurations of single-layer honeycomb spherical latticed shells. It is also suggested that the span should not exceed 40 m. The overall stability of the net shell is better and material utilization is higher, when the rise to span ratio is close to 0.25 and the bar length is about 2 meters. Meanwhile, the material nonlinearity has a great effect on the stability of the bearing capacity for single-layer honeycomb spherical latticed shells, and the bearing capacity of latticed shells is decreased by 50%. However, the critical load of latticed shells is reduced by 52% when the initial defects reach 1/150 of the span. Moreover, it is found that the reticulated shells are not sensitive to the asymmetric loads.

single-layer honeycomb spherical latticed shells; stability property; critical load; nonlinear analysis

1674-2974(2016)11-0033-06

2015-11-11

国家重点研发计划资助项目(2016YFC0701200，2016YFC0701201)；湖南省高校科技创新团队滚动计划资助项目(湘财教指(2015)616号)

贺拥军(1970-)，男，湖南宁乡人，湖南大学教授，博士†通讯联系人，E-mail:hyj0087@163.com

TU393.3

A