黏性土中倾斜荷载下抗拔桩的模型试验研究

杨明辉,杨学文,赵明华

(湖南大学 土木工程学院，湖南 长沙 410082)



黏性土中倾斜荷载下抗拔桩的模型试验研究

杨明辉†,杨学文,赵明华

(湖南大学 土木工程学院，湖南 长沙 410082)

为研究黏性土地基中抗拔桩在不同倾斜荷载情况下的承载机理,开展了抗拔桩室内模型承载试验.对比试验结果表明,抗拔桩承受倾斜荷载时,与竖向承载不同,呈现靠倾斜荷载一侧的桩周土体始终受压,而另一侧土体始终受拉的现象.达到极限时,仅靠荷载一侧桩周一定深度土体破坏,破坏区域在地表大致呈现扇形分布,其范围随荷载倾角增大而增大.此外,极限抗拔承载力随着倾角的增大而增大.在此基础上,依据破坏模式建立了倾斜荷载下抗拔桩的计算模型及桩周土体的破裂面方程,并基于单元体极限平衡分析得出了抗拔桩极限承载力计算公式．与试验结果对比表明,该方法计算值与实测值吻合较好.

黏性土;倾斜荷载;抗拔桩;模型试验;极限承载力

极限承载力分析是抗拔桩研究中最为关键的问题之一[1-2].目前相关研究主要集中在竖向荷载下的分析,但实际工程中,抗拔桩在承受竖向抗拔力的同时,极有可能承受水平向荷载从而构成倾斜荷载作用[3-4],此时,若仍采用规范方法而忽略水平向荷载作用,显然会造成一定偏差,可见研究倾斜荷载下抗拔桩的承载机理更为合理.

目前针对倾斜受荷抗拔桩承载机理的研究相对较少,主要为国外有关学者的研究.如Shin等[5]针对饱和黏性土中受倾斜荷载抗拔桩室内模型试验研究,通过试验得出极限承载力与荷载倾角关系的经验公式.Ayothiraman等[3]基于试验结果分析了承受竖向和水平联合荷载抗拔桩的极限承载力与桩顶位移的关系,认为尽管复合加载作用下抗拔桩的极限承载力会提高,但桩顶位移的约束会使其应用受限. Krishna等[6]则研究了桩顶压力对承受倾斜拉拔荷载的模型桩的影响,得出倾斜抗拔承载力会随桩顶压力成百分比的增加而降低.Patra等[4]在分析承受倾斜荷载抗拔群桩的极限承载力与相应竖向及水平极限承载力的极坐标关系图后,得出了可以预测倾斜受荷抗拔群桩极限承载力的半经验公式.Achmus等[7]通过数值模拟研究了非黏性土中水平和竖向荷载联合作用下的抗拔桩基性状,认为当竖向荷载远大于水平荷载时,水平荷载对桩身产生的较大正应力会使竖向极限承载力分力增大.

从以上研究可知,大部分均集中于对砂土中抗拔桩的分析,缺乏对倾斜荷载下抗拔桩的破坏模式的深入分析.本文针对特定条件下一定含水率非饱和黏性土地基中不同荷载倾角的抗拔桩进行模型试验,主要分析荷载倾角和桩长对倾斜荷载下抗拔桩极限承载力的影响,并在此基础上,探求其极限承载力的计算方法.

1 试验概况

1.1 试验装置

试验在模型箱中进行,模型箱几何尺寸为1 240 mm(L)×1 100 mm(W)×1 210 mm(H),桩轴线距模型箱内壁10D(以消除边界效应),D为桩直径.采用砝码加载,通过改变滑轮位置调整荷载角度,见图1所示.

图1 室内模型试验装置Fig.1 Laboratory model test arrangement

1.2 试验材料

本试验所用模型桩为低碳钢管,钢管外径30 mm,管壁厚2 mm,为探讨桩长的影响,选择了2种长度桩体,分别为0.75 m与0.90 m.为达到表面粗糙的效果,在桩外表面黏一层砂粒,如图2所示.

(a) 粘贴应变片后

(b) 粘贴砂粒后图2 模型桩Fig.2 Model piles

将模型桩桩端用薄钢板封口,并在荷载倾斜方向两侧打孔,沿模型桩不同深度粘贴应变片,应变片粘贴位置如图3所示,应变片粘贴于距桩端和桩顶分别为50 mm和100 mm的位置处,应变片之间的距离为150 mm.

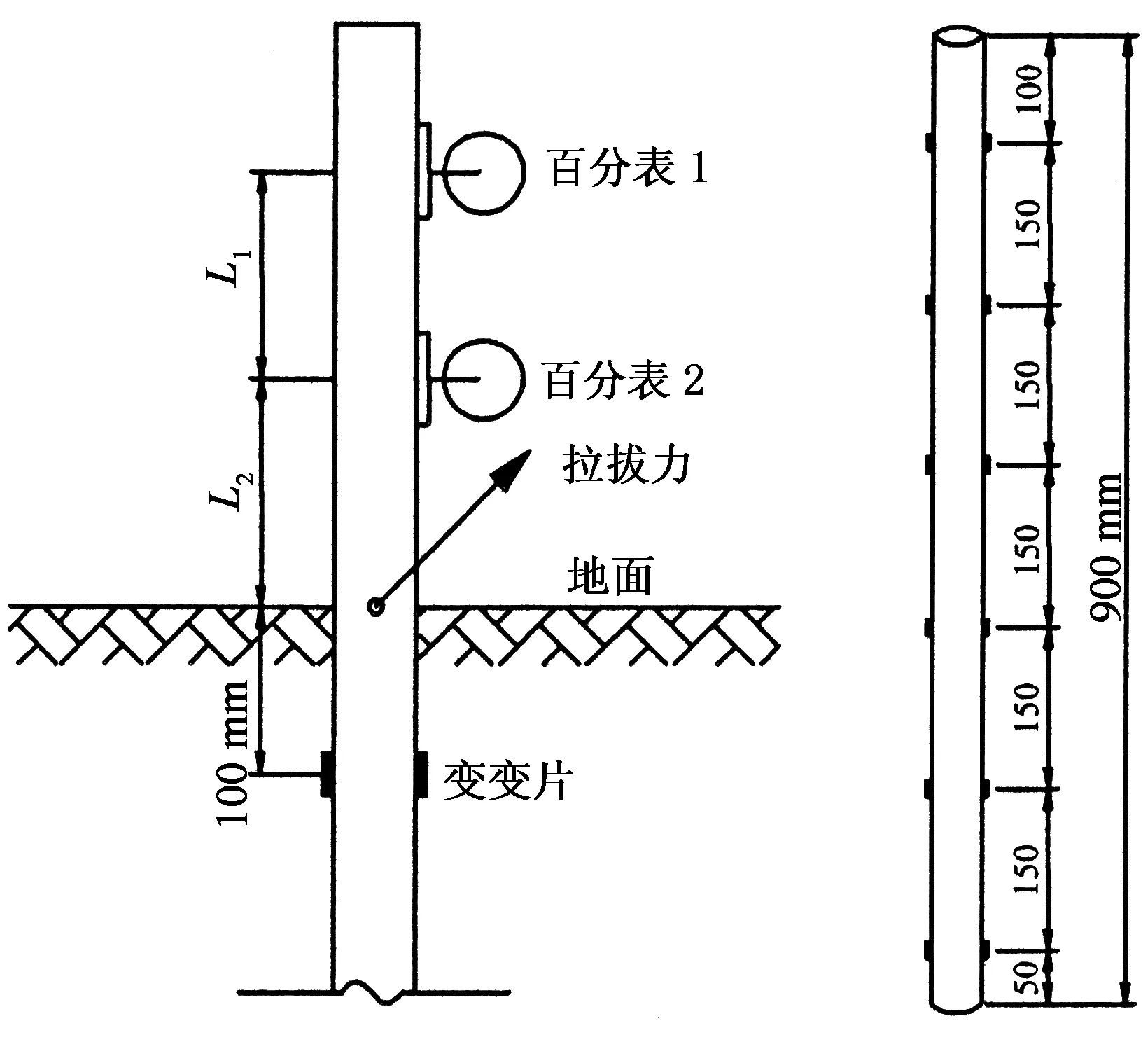
图3 水平位移测量和应变片粘贴位置Fig.3 Measurement of horizontal displacement and the position of strain gages

本试验所用黏性土为软黏土,人工压实,采用分层填筑,填筑厚度每层100 mm,为保证每层土体的一致性,每次夯实的土体重量要定量,预埋环刀以测土体密度.试验后取试验用黏性土进行土工试验,相关参数如表1所示.

表1 试验用黏性土参数Tab.1 Parameters of experimental clayey soil

1.3 试验方法

模型桩采用预先埋入法成桩,即先将桩固定在模型箱中一定深度,用木架导向使之保持竖直,再分层填筑.由柔性钢丝绳通过两个定滑轮连接桩顶和砝码.模型完成后架设百分表以进行桩顶竖向和水平位移量测,如图3所示,百分表1,2测得水平位移分别为Δ1,Δ2,因此桩顶的水平位移为

Δh=Δ1-(Δ1-Δ2)(L1+L2)/L1

(1)

式中:L1为百分表1与百分表2的测点距离,L2为百分表2测点到地面的距离.

本次模型试验采用慢速维持加载法.每级加载后,待位移稳定后再施加下一级荷载,并观察土体裂纹发展情况.试验终止加载标准以容许最大桩身地面水平位移或竖向位移达0.15D为标准[8-11].为探讨桩长及荷载倾斜角度的影响,本次试验共对8根单桩进行了抗拔试验,分2组进行(长径比25，30),每组4根(拉拔力倾斜角度α分别为0°,15°,30°,45°).

2 试验结果分析

2.1 倾斜荷载下抗拔桩的破坏模式分析

试验过程中,自地面开始出现裂缝至终止加载,近距离拍摄地面土体裂缝的开展情况,由此分析其破坏模式.试验结果表明,3种不同倾斜角度(15°,30°, 45°)下的抗拔桩破坏模式具有相似性,仅破裂面尺寸有差别.因此,如图4所示,本文仅给出长径比为25倾角为15°的试验图片,而表2列出了所有试验桩的破坏模式.由图4(a)可以看出,抗拔桩承载达到极限状态时,桩周土体出现明显裂缝.

桩周土体破坏区域与竖向荷载下作用不同,可以看出,在倾斜荷载作用下,桩周土体呈现向一侧破坏,且其破坏区域在地表大致呈现以桩轴心为顶点的扇形分布(图4(b)),而对破坏土体进行侧面开挖则可知,土体破坏仅发生在地表以下一定深度范围内(图4(c)).对试验过程的观察,得知荷载倾角为15°时,表面破坏土体裂缝(图4(a))发展缓慢,在土体接近完全破坏时才开始迅速发展;荷载倾角为45°时,表面土体裂缝就算在荷载很小时发展也会比较快.

表2中,H为破坏土体深度,r和圆心角分别为扇形表面破坏面半径和圆心角.可以看出,桩长一定时,随着荷载倾角的增大,破裂面尺寸H和r都逐渐变大,这表明破坏土体体积随荷载倾角的增大而增大.荷载倾角一定时,桩长较大的抗拔桩,无论是破坏土体的深度还是地表面的破坏面积,都大于桩长较小的抗拔桩,但不同荷载倾角下扇形圆心角大小相似.

2.2 桩身应变分析

图5为L/D=25,荷载倾角α=30°的抗拔桩在整个加载过程中的应变情况.应变1(1′)到应变8 (8′)为依次增加的荷载级数所对应的应变值,应变值正为受拉,反之受压.由图5可以看出倾斜荷载一侧的桩身始终受压,而另一侧始终受拉.这说明在实际工程设计中,不但要考虑抗拔桩材料的抗拉性能,还要考虑抗拔桩的抗压性能.且抗拔桩的整个受拉过程中,以桩顶以下一定深度处为临界点,在此深度范围内,受拉一侧的应变值沿桩顶向下逐渐减小,且始终大于受压一侧,而受压一侧的应变值逐渐增大.在整个加载过程中,在此临界点以下,两侧应变值(绝对值)的大小基本相似.

(a) 表面土体破坏模式

(b) 清理掉破坏土体后

(c) 破坏土体剖面图4 极限荷载时土体破坏模式(L/D=25，α=15°)Fig.4 Failure mode of soil surface about ultimate load表2 破坏面裂缝尺寸Tab.2 Crack size of failure surface

L/D倾角/(°)H/mmr/mm圆心角/(°)1545130160253050150167455417016615581501553030631701704572190165

图5 桩身应变分布曲线(L/D=25，α=30°)Fig.5 Strain distribution curves along pile

2.3 荷载-位移与极限承载力-倾角规律分析

图6为长径比为30的桩基竖向位移与荷载的关系曲线图.由图6可以看出,4种不同倾斜角度的荷载-竖向位移曲线形状基本类似.荷载较小时,荷载-竖向位移关系呈线性关系,而随着荷载的增大,荷载-竖向位移曲线逐渐转变为非线性直至达到极限.到达极限后,极小的荷载增量将导致位移急剧增大.

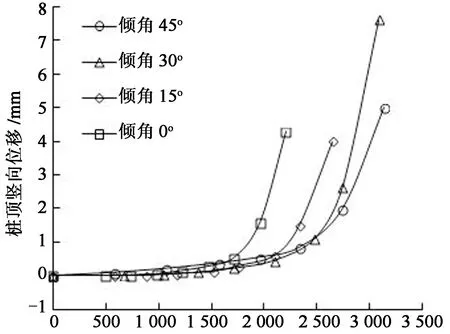
倾斜荷载/N图6 荷载与竖向位移曲线(L/D=30)Fig.6 Curves of uplift load versus vertical displacement

图7为长径比L/D=30的桩基水平位移与荷载的关系曲线图.由图可看出,在3种不同的倾角状况下,抗拔桩的水平位移都会随荷载的增加而增大.当倾角较大时就算增加很小的拉拔力也会产生较大水平位移,这与Das等[12]提出的结论相符,且倾角为30°和45°的曲线相当接近,但相较图6,3种荷载倾角下荷载-水平位移曲线转折点都不明显.

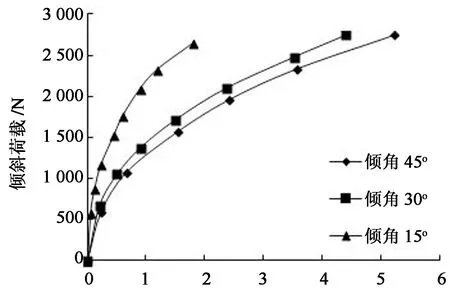
桩顶水平位移/mm图7 荷载与水平位移曲线(L/D=30)Fig.7 Curves of uplift load versus horizontal displacement

抗拔桩受倾斜荷载时,桩身拉伸产生与竖直方向成一定角度的倾斜向上位移.由图6与图7可以看出:荷载倾角为15°的抗拔桩,倾斜荷载小于2 352 N时,竖向位移始终小于水平位移,当倾斜荷载为2 352 N时,竖向位移开始大于水平位移.当倾斜荷载为2 646 N时,竖向位移为4 mm,水平位移为1.8 mm,竖向位移远大于水平位移.因此,对于荷载倾角为15°的抗拔桩,其终止加载标准可以由竖向位移判断.荷载倾角为30°和45°的抗拔桩,在破坏前的整个加载过程中,竖向位移始终小于水平位移.虽然其荷载-竖向位移曲线为陡升型,但在竖向位移突然急剧增大之前,水平位移已经达到终止加载标准.因此,对于荷载倾角为30°和45°的抗拔桩,要由水平位移来判断其终止加载标准.

图8为极限承载力与倾角的关系示意图.在以一定位移为标准控制极限承载力的前提下,随着倾角的增大,极限承载力也随之增大.倾角依次增大时,桩长0.90 m抗拔桩的极限承载力大于桩长0.75 m抗拔桩的极限承载力,这表明增加桩长能有效提高倾斜荷载下抗拔桩的极限承载力.

3 倾斜受荷抗拔桩的极限承载力分析

倾斜受荷抗拔桩极限承载力可以分解为竖向和水平分力.本文基于试验实测的破坏裂缝尺寸,对黏性土中倾斜荷载下抗拔桩破坏土体进行极限平衡分析.

荷载倾斜角度/(°)图8 极限承载力与倾斜角度的关系曲线Fig.8 Variation of ultimate capacity with angle of load inclination

考虑桩长径比对破坏模式的影响,对表2中的破坏面裂缝尺寸进行非线性最小二乘拟合,得出特定试验条件(试验缩尺比例与非饱和黏性土的含水率和强度等)下抗拔桩荷载倾角α与破坏尺寸的函数关系式:

H=0.017D(L/D)1.421e0.019sin α

(15°≤α≤45°)

(2)

r=0.548D(L/D)0.686e0.0125sin α

(15°≤α≤45°)

(3)

图9为倾斜荷载下抗拔桩的承载力计算简图,对倾斜承载力的竖向分力Pv与破坏面的应力平衡关系进行研究.

图9 承载力计算简图Fig.9 Diagram of capacity

首先取破坏土体深度H内的一个单元进行极限平衡分析,作用在单元滑动面上的法向应力ΔR,滑动面长度为ΔL,切向阻力为ΔT为

ΔT=ΔRtan φ+cΔL

(4)

(5)

(6)

式中:θ为破坏面切线与x轴夹角;破坏土体在外力作用下推向地基土,则Kp为滑动面上的侧向土压力系数,且Kp=tan2(45°+φ/2);γ为土体重度,假定地面以下H范围内桩的重度与土体重度相等.根据单元土体的静力平衡关系,可得

(Pv+ΔPv)-Pv+μqπx2-

μπ(q+Δq)(x+Δx)2-ΔW-

2μπ(x+Δx/2)ΔTsin θ=0

(7)

式中:x为破坏面上任一点到桩轴心的距离,且x=(H-Z)/tan θ；μ为表2试验实测扇形破坏面的圆心角与圆周之比,且μ=0.454.

将式(6)代入式(7),可得

(8)

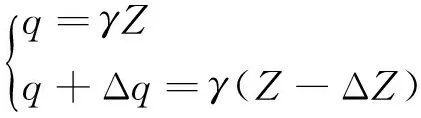
(9)

Δq=-γΔZ.

(10)

将式(10)代入式(8) ,取极限得:

(11)

倾斜荷载下抗拔桩由埋深H到桩端的破坏面为沿桩-土界面以外一定厚度土体内的圆柱形破坏,圆柱状剪切破坏时抗拔桩的承载力计算公式为

(12)

式中:Wp为桩的重量,L为桩的长度.桩侧最大剪应力τmax(z)可以表示为

(13)

由倾斜承载力与其竖向分力Pv的关系得出倾斜荷载下抗拔桩的极限承载力计算公式

(15°≤α≤45°).

(14)

计算得长径比为25和30的倾斜受荷抗拔桩在不同倾斜角度下的极限承载力,将其与实测值进行比较,如图10所示.可见使用式(14)得到的理论值与实测值非常接近.由图还可以看出,倾角为15°和30°时极限承载力计算值大于实测值,而倾角45°时计算值却小于实测值,这可能是由于计算值是基于破坏模式,而实测值基于桩顶位移.

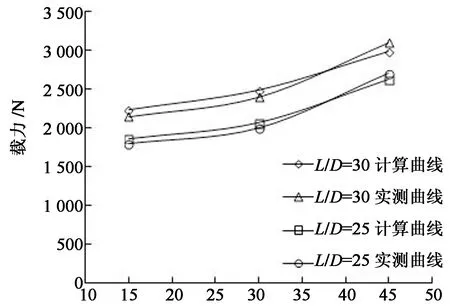
荷载倾斜角度/(°)图10 计算曲线与实测曲线的比较Fig.10 Comparison of theoretical curves and measured curves

4 结 论

本文开展了黏性土中抗拔桩的倾斜荷载承载试验,得到以下结论:

1)倾斜荷载作用下,其破坏模式为靠荷载一侧桩周土体破坏,破坏区域在地表大致呈现扇形分布,其范围随荷载倾角增大而增大,破坏深度也随荷载倾角增大而增大.

2)抗拔桩的极限承载力与荷载倾角及长径比紧密相关.在荷载大小相同情况下,极限承载力随荷载倾角及长径比的增大显著提高.

3)考虑荷载倾角和桩长径比,对破坏面裂缝尺寸进行非线性最小二乘拟合得到破裂面方程,用极限平衡方法由倾斜承载力与相应的竖向分力的关系导得了黏性土中倾斜荷载作用下抗拔桩极限承载力计算公式,计算值与实测值对比吻合良好.

[1] 何思明.抗拔桩破坏特性及承载力研究[J].岩土力学,2001,22(3): 308-310.

HE Si-ming. Study on bearing capacity and failure of uplift pile[J]. Rock and Soil Mechanics, 2001, 22(3):308-310. (In Chinese)

[2] 朱碧堂,杨敏.抗拔桩的变形与极限承载力计算[J].建筑结构学报, 2006,27(3):120-129.

ZHU Bi-tang, YANG Min. Calculation of displacement and ultimate uplift capacity of tension piles[J]. Journal of Building Structures，2006,27(3):120-129. (In Chinese)

[3] AYOTHIRAMAN R, REDDY K M. Model experiments on pile behaviour in loose-medium dense sand under combined uplift and lateral loads[J]. Tunneling and Underground Construction, 2014, 242:633-643.

[4] PATRA N R, PISE P J. Model pile groups under oblique pullout loads-an investigation[J]. Geotechnical and Geological Engineering, 2006, 24:265-282.

[5] SHIN E C, DAS B M, PURI V K,etal. Ultimate uplift capacity of model rigid metal piles in clay[J]. Geotechnical and Geological Engineering, 1993, 11:203-215.

[6] KRISHNA B, PATRA N R. Effect of compressive load on oblique pull-out capacity of model piles in sand[J]. Geotechnical and Geological Engineering, 2006, 24: 593-614.

[7] ACHMUS M, THIEKEN K. On the behavior of piles in non-cohesive soil under combined horizontal and vertical loading[J]. Acta Geotechnica, 2010, 5:199-210.

[8] GB 50007-2011 建筑地基基础设计规范[S]. 北京：中国建筑工业出版社，2011:136-138.

GB 50007-2011 Code for design of building foundation[S].Beijing: China Building Industry Press, 2011:136-138. (In Chinese)

[9] JTG D63-2007公路桥涵地基与基础设计规范[S]. 北京:人民交通出版社,2007：66-111.

JTG D63-2007 Code for design of ground base and foundation of highway bridges and culverts[S]. Beijing: China Communications Press, 2007: 66-111. (In Chinese)

[10]刘祖德. 抗拔桩基础[C]//刘金励主编. 桩基工程技术. 北京：中国建材工业出版社，1966：642-674.

LIU Zu-de. Uplift pile foundation [C]//LIU Jin-li. Pile Foundation Engineering Technology. Beijing: China Building Materials Press, 1966：642-674.(In Chinese)

[11]MEYERHOF G G, YALCIN A S. Pile capacity for eccentric inclined load in clay[J]. Canadian Geotechnical Journal, 1984, 21(3):389-396.

[12]DAS B M, SEELEY G R, RAGHU D. Uplift capacity of model piles under oblique loads[J]. Journal of Geotechnical & Geoenvironmental Engineering,1976, 102(9):1009-1013.

[13]赵明华, 雷 勇, 刘晓明. 基于剪切位移法的基桩负摩阻力计算[J]. 湖南大学学报：自然科学版，2008, 35(7): 1-6.

ZHAO Ming-hua, LEI Yong, LIU Xiao-ming. Settlement calculation of single pile's negative skin friction with shear displacement method [J]. Journal of Hunan University: Natural Sciences, 2008, 35(7): 1-6. (In Chinese)

[14]龚晓南，王继成，伍程杰. 深基坑开挖卸荷对既有桩基侧摩阻力影响分析[J]. 湖南大学学报：自然科学版，2014, 41(6): 70-76.

GONG Xiao-nan, WANG Ji-cheng, WU Cheng-jie. Effect of unloading on the shaft resistance of existing piles due to excavation[J]. Journal of Hunan University: Natural Sciences, 2014, 41(6): 70-76. (In Chinese)

[15]姚笑青. 桩基设计与计算[M]. 北京：机械工业出版社，2014：43-44.

YAO Xiao-qing. Design and calculation of pile foundation[M]. Beijing: China Machine Press, 2014：43-44. (In Chinese)

Study of Model Experiments on Uplift Piles in Clay under Oblique Loads

YANG Ming-hui†, YANG Xue-wen, ZHAO Ming-hua

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China )

Laboratory model tests on steel piles embedded in cohesive soil were carried out to study the transformation law in relation to ultimate uplift capacity and displacement patterns of uplift piles subjected to oblique loads. The test results show that the side of the pile near the oblique load is always under pressure, while the other side is in tension all the time, which differs from the uplift pile subjected to vertical loads. After reaching the ultimate capacity, soil in some depth is cracked only around the side close to oblique load. The failure surface occurs below the top of the pile. The failure area on the earth surface is distributed as a fan, whose range becomes larger with the increasing inclination of loads. Meanwhile, the ultimate capacity of piles increases with the increase of the inclination angle. On this basis, the calculation model of uplift piles subjected to oblique loads and the formula of failure surface around the pile were established based on the failure mode. Moreover, according to the analysis on the equilibrium conditions of the soil element, a formula for estimating the oblique capacity of uplift piles in clay soil subjected to oblique loads was also proposed. The predictions agree well with the test results so that the formula can be used in practical engineering.

clay; oblique loads; uplift piles; laboratory tests; ultimate capacity

1674-2974(2016)11-0013-07

2015-11-26

国家自然科学基金资助项目(51278184，50708030), National Natural Science Foundation of China(51278184，50708030)；教育部新世纪优秀人才支持计划(NCET-13-194)；湖南省科技重点研发项目(2015CK3003)

杨明辉(1978-)，男，湖南武冈人，湖南大学副教授†通讯联系人，E-mail: yamih@126.com

TU473.1

A