温度对包带式星箭连接分离装置预紧力的影响
唐 杰, 张 修 科, 李 新 宽, 韩 涵, 白 瑞 祥
( 1.上海宇航系统工程研究所, 上海 201109;2.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024 )
温度对包带式星箭连接分离装置预紧力的影响
唐 杰1, 张 修 科1, 李 新 宽1, 韩 涵1, 白 瑞 祥2
( 1.上海宇航系统工程研究所, 上海 201109;2.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024 )
为有效评估温度对包带式星箭连接分离装置的预紧力的影响,基于传统包带预紧力计算方法,通过引入温度影响系数,提出了考虑温度效应的计算公式。由于包带式星箭连接边界条件的复杂性,温度影响系数难以通过理论计算准确得出,本文将有限元数值仿真方法与高低温试验相结合,拟合出小型包带装置的温度影响系数。结果表明,预紧力的计算值与实验值较为吻合,为此类结构包带预紧力的精确计算提供了参考工具,并为多种规格包带装置的温度影响系数的确定提供了有效解决方法。
温度效应;包带;预紧力;有限元
0 引 言
包带式星箭连接分离装置作为航天领域应用最为广泛的星箭连接和解锁结构,是运载火箭、上面级等运载器发射有效载荷的重要组成部分,其预紧力的大小对星箭连接可靠度具有重要影响[1],并影响到有效载荷的分离冲击。预紧力过小,则无法满足星箭连接的刚度要求;预紧力过大,则星箭分离冲击环境恶劣[2-4],甚至对星箭连接结构造成破坏。因而准确的预紧力加载是保证有效载荷发射任务圆满成功的必要条件。
NASA于1999年《包带系统设计准则》中提出采用包带预紧力简化公式[5],该公式以夹块与对接框出现相对径向滑移作为失效判据。唐乾刚等[6]根据星箭连接处受力情况及包带装置特点,导出了包带装置预紧力计算公式。但以上预紧力计算公式均未考虑温度变化对预紧力的影响。火箭因飞行过程中气动加热和滑行段空间辐射,包带装置一般处于温度交变的环境当中,环境温度的差异、复杂的边界条件、不同材料的线膨胀系数都使得包带预紧力发生变化,特别对于预紧力承载需求较小的小规格包带装置,温度变化的影响将占主要因素。因此,单纯通过文献中理论计算得到的包带预紧力有一定的局限性,必须将温度对包带预紧力影响考虑进去。
目前,国内外温度对简化的混凝土箱体结构[8]、复合材料板壳结构[9]应力影响分析,包带结构的有限元建模及动力学分析[10-13]等方面均做出了较为深入的研究,然而基于有限元方法针对温度对包带结构预紧力的影响方面尚未有相关研究工作。鉴于此,本文提出了考虑温度效应的包带预紧力计算方法,对传统计算公式进行了修正,并通过对小型标准Ф300接口包带及星箭加载结构进行了有限元仿真和温度实验,并通过温度实验进行验证,拟合出公式中的温度系数,讨论了温度对包带预紧力的影响规律。
1 Ф300包带装置紧力计算模型和方法
Ф300包带星箭连接分离装置采用标准接口[14],主要包括2个钛合金条带、12个铝合金夹块(与星箭承载结构材料相同)、4个2A14铝合金加载接头和2枚分离火工品等。其预紧力的加载主要通过旋转火工品螺母进行,并通过预紧力监测系统读取该包带中部应变值,经分析计算后获得预紧力实际加载值。根据试验标准[15],星箭连接分离装置需覆盖火箭飞行过程中的温度变化范围为-40~70 ℃。
1.1 预紧力计算公式
NASA于1999年《包带系统设计准则》中提出采用包带预紧力简化公式[5]为:
F=wD(tanβ-μ)/(1+μtanβ)
(1)
(2)
式中:D为对接框直径;β为夹块斜面角度;μ为夹块与对接框接触面摩擦系数;w为连接面的线载荷;Faxial,M分别为连接面所受的轴向力和弯矩。
进一步考虑温度对包带预紧力的影响,则需对传统理论公式进行修正:
F0=F1+F2
(3)
F2=fkp(-ΔT)
(4)
式中:F0为包带装置总预紧力;F1为理论计算值;F2为由温度变化带来的预紧力修正值;f为安全系数;kp为温度影响系数;(-ΔT)为星箭分离时刻与地面预紧力加载时刻环境温度差。
公式(4)中kp是影响计算精度的关键系数,由于边界条件复杂,且需考虑夹块、条带间的摩擦等因素,目前没有精确的数学计算模型。虽然采用高低温实验方法可得到kp,但该方式具有周期长、经济性差、人力耗费大的缺点,影响了工程研制的进度。借助于目前已十分成熟的有限元数值仿真技术和大型软件平台,在已知材料的弹性参数和温度参数的情况下,通过数值仿真精确地计算出结构的预紧力影响系数kp是可行的。
1.2 温度影响系数的计算
以Ф300包带星箭连接分离装置为例,以下给出温度影响系数的计算方法。
1.2.1 材料参数
包带装置的结构材料性能如表1所示。


表1 材料力学性能
1.2.2 有限元模型
在高低温环境中,包带装置中面与星箭结构分离面保持在同一水平面内,并均为中心轴对称结构,各主要零件配合面润滑良好,主要零件的材料不同,如表1所示。各零件因材料温度膨胀系数不同产生相对变形是导致包带预紧力变化的主要因素。
为有效模拟该真实温度变形情况并简化计算,综合计算资源和模型直观性[17-20],该Ф300包带星箭连接分离装置采取如下建模方式:
(1)模型:全尺寸1∶1整体建模,消除因模型简化造成的意外误差。
(2)边界条件:建立中心对称约束和星箭对接面对称约束,以利于有限元模型的计算收敛,并提高仿真准确度。
(3)网格:条带采用S4R四边形壳单元模拟,该单元性能稳定,适合接触计算。夹块、星箭对接框、条带接头结构等实体结构均采用C3D8I六面体Hex单元,并将夹块与条带接触面两端刚度变化剧烈的区域进行网格细化,以降低该处的应力集中。
(4)零件配合面:条带与夹块配合面采用接触模拟,摩擦系数取0.2,其余配合面均采用绑定模拟。接触面摩擦不考虑。
(5)载荷施加过程:初始状态,温度载荷为20 ℃,并施加2 100 N螺栓载荷模拟初始预紧力。然后,温度降低至-40 ℃,之后以每分析步增加10 ℃增至70 ℃,通过读取各分析步中条带典型截面单元应力得到包带预紧力值。
模型建立并进行网格细化后,该装置有限元模型如图1所示。

图1 Ф300包带装置及星箭结构模型
Fig.1 Finite element model of Ф300 clamp band mechanism with satellite and launch vehicle structure
1.2.3 计算结果及分析
在预紧力2 100N时,Ф300包带装置应力随着温度每10 ℃梯度升高均呈现均匀增大趋势,如图2、3、4所示。

图2 包带装置应力云图(20 ℃)

图3 条带应力云图(20 ℃)


a) -40 ℃ (b) 20 ℃ (c) 70 ℃
由图4可知,(1)70 ℃状态下包带预紧力相比于最初20 ℃加载状态,预紧力增加48.5%;-40 ℃ 状态下预紧力降低-51.3%,表明温度变化对该Ф300包带式星箭连接分离装置预紧力具有重要影响。(2)条带与夹块接触的中部应力较大,上下端面较小,可见预紧力监测系统采集点如仅设置在条带中部,并以条带整个截面均匀变形为前提进行预紧力计算,会导致实验测试结果偏大,实际预紧力并未达到设计要求值。
为保持与实验状态一致,仍提取条带中部应力值进行预紧力温度影响分析,结果如图5所示,其中横坐标为温度,纵坐标为预紧力,拟合方程见图5中公式。
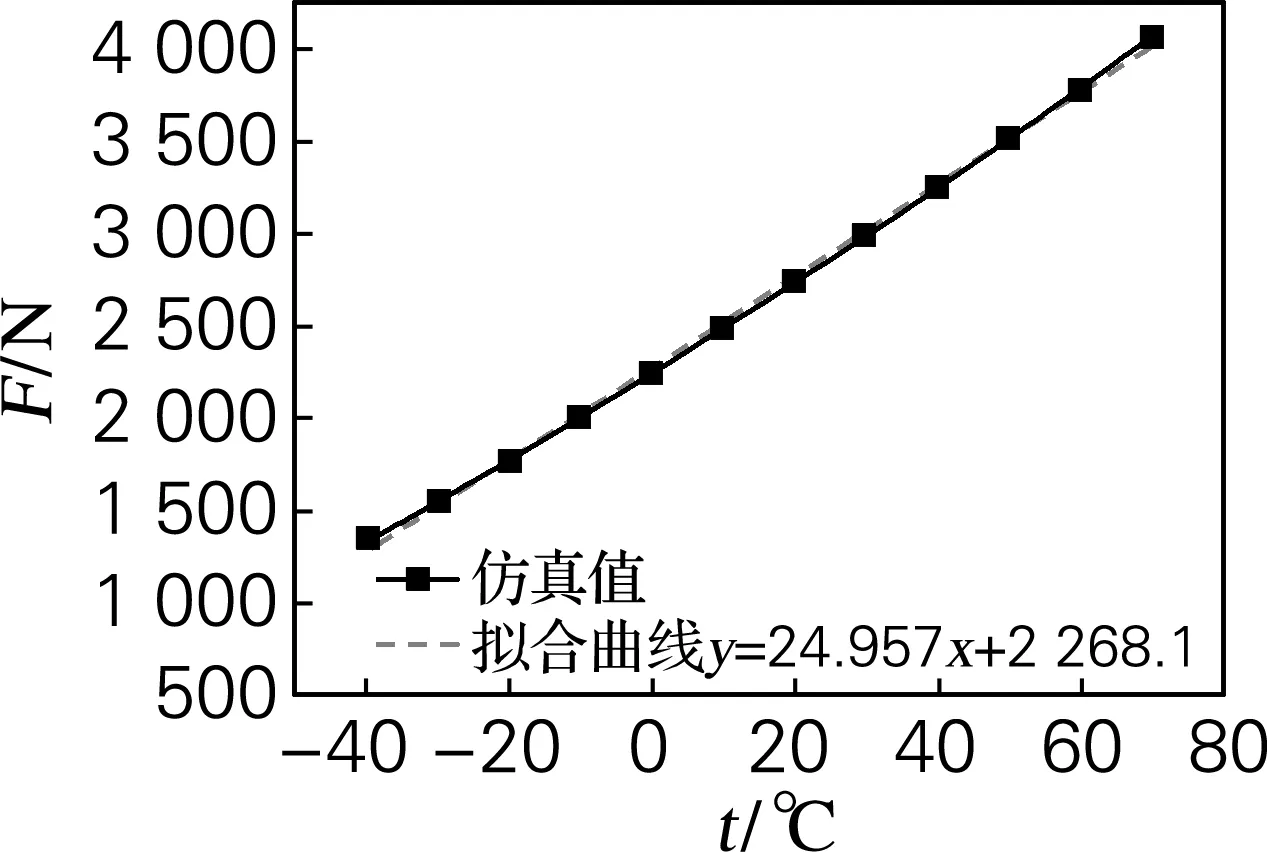
图5 预紧力-温度关系有限元分析结果
拟合直线斜率表明了包带预紧力随温度的变化,即仿真分析温度影响系数kp=24.96 N/℃。
2 实验验证
为验证上述有限元模型处理方式的准确性,以与计算模型结构相同的实验产品进行高低温实验验证。为消除由单次实验带来的误差,温度实验共进行3次,并通过预紧力监测系统[21]进行预紧力全程跟踪测试。
从20 ℃室温,进行预紧力加载后,将整套装置水平放入温度箱,不作任何约束。为了消除环境温度与产品温度偏差,在整个实验过程中,除了对产品周围空间环境温度进行实时监控外,同时在包带产品夹块间隙的条带中部和星箭加载结构上粘贴温度传感器,直接测量产品实际温度。
实验温度定为-40~70 ℃,共分为12等级,温度变化梯度为10 ℃,与仿真分析一致。在每级环境温度下保温2 h。
第1次温度实验预紧力实测值如表2所示。由表2可知:(1)相比于初始20 ℃加载状态,70 ℃ 状态下的包带预紧力增加49.5%;-40 ℃状态下包带预紧力降低58.2%,表明温度变化对该Ф300包带式星箭连接分离装置预紧力具有重要影响。(2)产品温度与环境温度存在温差,最大温差仅为0.1 ℃,表明产品温度与环境温度具有良好的一致性,可将环境温度作为数据处理温度,并与仿真结果进行比较分析。


表2 第1次实验预紧力测试结果
针对3次实验结果,按实测的环境温度和预紧力平均值做出散点图并进行线性拟合,如图6所示,其中横坐标为温度,纵坐标为预紧力,拟合方程见图6中公式。
通过对实验数据拟合,条带的预紧力温度影响系数汇总如表3所示。根据表3结果,取3次实验的温度影响系数的均值作为Ф300包带装置温度影响系数,即Φ300包带在环境温度-40~70 ℃,预紧力随温度升高呈线性增加趋势,温度对包带预紧力的实验测试影响系数为kp=25.9 N/℃。


a) 第1次 (b) 第2次 (c) 第3次


表3 实验温度影响系数
仿真分析结果kp=24.96 N/℃与温度实验结果相比较为一致,偏差度3.6%。
3 结 论
(1)温度是影响包带装置预紧力的重要因素。对Φ300包带装置预紧力计算公式进行修正,提出了温度影响系数,为24.96 N/℃,为包带式星箭连接装置预紧力精确计算奠定了基础;
(2)提出了包带装置温度系数有限元仿真分析方法,并经过了实验验证。该方法可应用包带预紧力温度系数的确定。
[1] 袁家军.卫星结构设计与分析[M].北京:宇航出版社,2004.
[2] 韩晓健,焦安超.包带低冲击装置冲击试验及数据分析[J].航天器环境工程,2007,24(5):318-321.
[3] LANCHO M, LARRAURI I. CRSS: a separation system for launching very heavy payloads[J]. Acta Astronautica, 2000, 47(2/3/4/5/6/7/8/9): 153-162.
[4] DOWEN D, CHRISTIANSEN S. Development of a reusable, low-shock clamp band separation system for small spacecraft release applications[C]//9th European Space Mechanisms and Tribology Symposium. Liège: European Space Agency, 2001: 191-198.
[5] NASA. Marman clamp system design guidelines: GD-ED-2214[S]. Maryland: NASA Goddard Space Flight Centre, 2000: 21-23.
[6] 唐乾刚,孙世贤.包带式星箭装置预紧力分析[J].国防科技大学学报,1996,18(2):20-25.
[7] 杨新峰.包带锁紧结构的预紧力确定[J].航天器环境工程,2009,26(6):122-127.
[8] 汪剑,方志.混凝土薄壁箱梁温度效应的变分解[J].计算力学学报,2008,25(2):207-211.
[9] 丁克伟,唐立民.任意厚度层合闭口柱壳的轴对称温度应力[J].计算力学学报,1998,15(2):162-173.
[10] 白绍竣,梁鲁.包带连接力学分析与建模[J].上海航天,2011,28(6):45-48.
[11] 秦朝烨,褚福磊.包带连接特性及星箭包带连接结构耦合动力学的研究进展[J].力学进展,2012,42(4):438-444.
[12] 谭雪峰,阎绍泽.包带式星箭连接结构的动力学模拟及故障分析[J].清华大学学报,2010,50(8):1205-1209.
[13] 白绍竣,尉飞.包带连接建模与非线性动力学特性分析[J].振动与冲击,2010,29(5):5-11.
[14] 国防科学技术工业委员会.包带弹簧式星箭连接分离装置通用规范:GJB2499A-2006[S].北京:国防科工委军标出版发行部,2007:12-13.
[15] 徐建强.火箭卫星产品试验[M].北京:中国宇航出版社,2012.
[16] 华国强.金属材料手册[M].上海:上海航天技术研究院,2007.
[17] 朱伯芳.有限单元法原理及应用[M].2版.北京:中国水利水电出版社,1998.
[18] 庄茁.基于ABQUS的有限元分析和应用[M].北京:清华大学出版社,2011.
[19] 王勖成.有限单元法[M].北京:清华大学出版社,2003.
[20] JACOB I R, VINAY K G, NICHOLAS E M. Techniques for finite element analysis of clamp band systems[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. California: AIAA, 2009: 1-9.
[21] 苏明照.DAS-1星箭包带应力监视系统[J].实验力学,1993,8(2):97-101.
Influence of temperature on clamp band’s pre-tightening force
TANG Jie1, ZHANG Xiuke1, LI Xinkuan1, HAN Han1, BAI Ruixiang2
( 1.Shanghai Aerospace System Engineering, Shanghai 201109, China; 2.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China )
A formula to calculate the pre-tightening force in the clamp band connecting/release mechanism with the temperature effect was proposed by introducing a factor into the typical equations. It was difficult to determine the temperature effect by means of theory analysis due to the complexity of boundary conditions within the connection, so series of temperature for mini-type clamp band equipments were given through combining the FEM simulations with the high/low temperatures. The results showed that these factors were suitable and effective for the pre-tightening force calculation for many kinds of clamp bands.
temperature; clamp band; pre-tightening force; simulation analysis
2015-04-20.
国家重点基础研究发展计划(973计划)项目(2014CB046506).
唐 杰(1980-),男,高级工程师,E-mail:kangqiaolaojie@sina.com.
V421.7
A
1674-1404(2016)06-0494-05
TANG Jie, ZHANG Xiuke, LI Xinkuan, HAN han, BAI Ruixiang. Influence of temperature on the clamp band’s pre-tightening force[J]. Journal of Dalian Polytechnic University, 2016, 35(6): 494-498.

