城市轨道交通网络脆弱性分析

曲迎春，徐仲之，龚航，黄智仁，王璞

(中南大学 交通运输工程学院，湖南 长沙 410075)



城市轨道交通网络脆弱性分析

曲迎春，徐仲之，龚航，黄智仁，王璞

(中南大学 交通运输工程学院，湖南 长沙 410075)

城市轨道交通网络是城市公交系统的重要组成部分。以北京地铁和深圳地铁为研究对象，建立两个城市的轨道交通网络模型，利用两个城市的地铁乘客刷卡数据，估计城市轨道交通需求OD；基于复杂网络理论分析两个城市轨道交通网络的拓扑结构，提出城市轨道交通网络脆弱性的评价指标；建立城市公共交通双层网络，对城市轨道交通网络的脆弱性进行更深层次的分析。研究结果表明:北京市与深圳市轨道交通网络脆弱边地理分布很相似，深圳市轨道交通网络平均而言更加脆弱；轨道交通网络的脆弱性与其网络复杂度密切相关；城市常规公交网络可以降低城市轨道交通系统的脆弱性。

地铁乘客刷卡数据；轨道交通网络；OD估计；脆弱性

随着我国小汽车保有量的快速增长，城市交通拥堵日趋严重，很多城市的交通管理部门都开始鼓励市民使用公共交通出行。城市轨道交通速度快、运量大，是公共交通系统的骨架。然而，城市轨道交通系统结构日趋复杂、运载量不断增大，故障、自然灾害等突发情况会对轨道交通系统造成严重威胁[1-3]。例如：2011年12月22日北京地铁1号线突发信号故障，导致列车中断运营1 h；2014年5月4日南京地铁4号线九华山基站坑发生渗水事故，造成北京东路九华山段由东向西交通一度中断；2015年7月28日上海地铁1号线锦江乐园至徐家汇方向突发供电故障，造成大量乘客滞留。城市轨道交通系统的可靠性是关系人民生活和社会经济发展的重要问题，受到了科学与工程领域学者的广泛关注[4-7]。

利用复杂网络理论与统计学方法，很多学者对城市轨道交通网络的拓扑结构进行了深入研究。高洁等[8]根据城市轨道交通网络受到外界攻击后运营能力的改变，定义了城市轨道交通网络系统抗毁可靠性，将站点子系统和区间子系统受到破坏后对客流量的影响作为评价依据。王志如等[9]选取最大连通OD数目、路径长度以及乘客换乘次数作为地铁网络脆弱性的评价指标，在仿真模型中分别对地铁车站和区间线路进行随机攻击和蓄意攻击，发现车站在蓄意攻击时具有脆弱性，区间线路在蓄意攻击时具有鲁棒性。张建华等[10]对上海市轨道交通网络的连通性和鲁棒性进行了研究，分析了单条地铁线上的站点受到攻击时地铁网络的连通性，发现介数较大的站点受到攻击时对网络的影响较大。孙剑等[11]对上海市轨道交通网络换乘站点的脆弱性进行分析，建立了基于客流量的换乘站点脆弱性的综合评价指标模型，定位了10个最脆弱的换乘车站。邓勇亮等[12]验证了南京地铁网络既具有小世界属性也具有无标度属性，并利用全网效率和平均最短路径来度量网络的脆弱性，结果显示南京地铁网络在随机攻击下表现了较强鲁棒性，但在刻意攻击下却很脆弱。

本文首先建立北京市和深圳市的轨道交通网络模型，利用北京市和深圳市的地铁乘客刷卡数据，估计了早高峰轨道交通需求OD；然后，分析现阶段两个城市轨道交通网络的拓扑结构，研究了轨道交通站间区间故障对乘客出行可达性及出行时间的影响；最后，基于深圳市地铁网络和公交网络建立了城市公共交通双层网络模型，更精确地评价了轨道交通网络的脆弱性。

1 城市轨道交通网络拓扑建模及OD估计

北京市和深圳市的轨道交通网络具有不同的拓扑结构特征。本文提出了两个脆弱性评价指标，对两个城市轨道交通网络的脆弱性进行分析，分析了两个轨道交通网络脆弱性的共性规律和异同特征，挖掘轨道交通网络脆弱性和网络结构间的关系。表1是北京地铁和深圳地铁的一些基本信息。

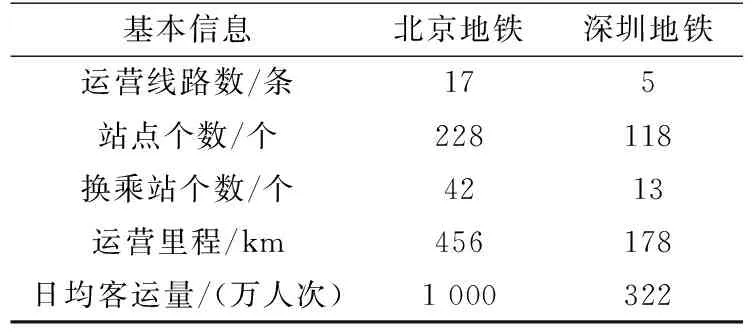
表1 北京地铁和深圳地铁的基本信息表

1.1 城市轨道交通网络拓扑建模

结合图论中有向图模型，将城市交通网络抽象为由节点和连边构成的有向图G=(V,E)，集合V中的元素为图G的节点集合，集合E中的元素为图G的边(线)集合，集合E中的元素由集合V中的任意两点连接产生。在城市轨道交通网络中，节点表示城市轨道交通车站，有向边表示城市轨道交通网络的站间区间。

本文利用Google Earth软件采集地铁站点的经纬度坐标，根据站点间的空间拓扑关系构建了北京市和深圳市的轨道交通网络(图1(a) & (b))。北京市轨道交通网络包含228个节点、507条边，深圳市轨道交通网络包含118个节点、252条边。根据轨道交通运营时刻表，我们计算了各个站间区间的运行时间，用于表示边的权重。为了更加准确地计算乘客出行时间，我们还收集了不同线路间的换乘时间信息。

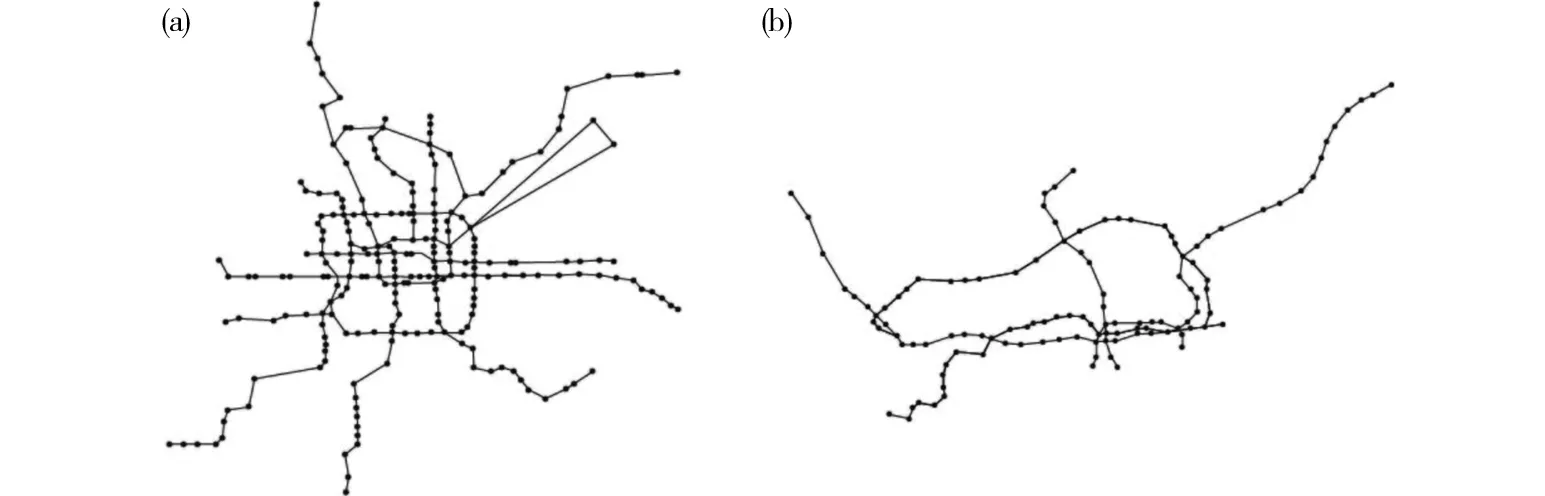
(a)北京市轨道交通网络;(b)深圳市轨道交通网络图1 城市轨道交通网络Fig.1 Urban rail transit network

1.2 轨道交通出行OD估计

本文使用北京市和深圳市某工作日的地铁乘客刷卡数据估计轨道交通出行OD，乘客刷卡数据记录了乘客编号、进站时间与站点、出站时间与站点。北京市和深圳市的乘客刷卡量呈现双驼峰分布(图2(a)和(b))，早高峰(8:00～9:00)和晚高峰(18:00～19:00)的出行量明显高于其他时段的出行量。本文选取早高峰时段为研究时段。

筛选早高峰(8:00～9:00)使用地铁出行的乘客刷卡记录，这些出行记录分为4种类型：1)8:00以后出发，9:00之前到达；2)8:00之前出发，9:00之前到达；3)8:00以后出发，9:00以后到达；4)8:00之前出发，9:00以后到达。类型1出行的进站时间和出站时间均在8:00～9:00之内，出行起点(O)与出行终点(D)不变。对于类型2、3、4，计算乘客起终点之间的最短路径，选择在8:00～9:00第一次和最后一次经过的站点作为新的出行起点(O)和出行终点(D)，从而获得的北京市和深圳市轨道交通网络在早高峰时段的出行需求OD分布，两市轨道交通早高峰时段出行总量分别为：2 113 378人次，203 882人次。

(a)北京市时变交通需求;(b)深圳市时变交通需求图2 时变交通需求Fig.2 Time-varying passenger volume

2 城市轨道交通网络的拓扑结构分析

2.1 节点度

复杂网络中节点度ki定义为与节点直接相连的边的数目，节点度的大小也表征了网络中各节点的中心性，其平均值在一定程度上反映了整个网络拓扑结构的连接复杂度，是网络结构特征最直接的度量[14]，节点度的计算如公式(1)所示：

(1)

式中：aij表示节点i与节点j之间是否存在边，若存在，则aij=1，否则aij=0；

北京市和深圳市的轨道交通网路站点的度分布如图3a，两个城市轨道交通网络80%以上的站点度为2，大部分站点为非换乘站点，平均节点度分别为2.23和2.13，节点度大于3的站点占比分别为14.9%和11%，最大度分别为5和4。从节点度计算结果来看，北京市轨道交通网络的复杂度高于深圳市轨道交通网络的复杂度，度值较大的节点占比较高。

2.2 边介数中心度

复杂网络中的边介数中心度bc定义为网络中所有最短路径中经过该边的路径的数目占最短路径总数的比例，反映了边在整个网络中的拓扑重要程度[15]。边介数中心度的计算如式(2)所示：

(2)

式中：σst表示任意两节点s和t之间的最短路径总数；σst(v)表示最短路径中通过边v的次数。

北京市和深圳市的轨道交通网络的边介数中心度都近似服从高斯分布，如图3(b)所示，北京：P(bc)=0.108 8e-((bc-0.028)/0.029)2，深圳：P(bc)=0.085 2e-((bc-0.047 5)/0.056 2)2。北京地铁的平均边介数中心度(0.029)小于深圳地铁的平均边介数中心度(0.054)。从边介数中心度的分布情况来看，北京市轨道交通网络边的平均可替代性要高于深圳轨道交通网络边的平均可替代性。

2.3 最短路径及平均最短路径长度

最短路径又称为测地路径，在加权有向网络中两个节点之间的最短路径指连接这两个节点的边的权值之和最小的路径，最短路径长度指两个节点的最短路径上的边的权值之和。平均最短路径长度L定义为任意两个节点之间的距离的平均值，计算式如(3)所示：

(3)

式中：L表示网络节点数；dij表示任意节点i与节点j之间的最短路径长度。

北京市和深圳市轨道交通路网中的边权重为相邻站间区间的运行时间，网络中最短路径长度即为两个车站最短路径间的运行时间之和，单位为分钟。经测量，北京市与深圳市的轨道交通网络的最短(时间)路径长度分布服从高斯分布(图3c)，北京:P(L)=0.116 6e-((L-34.53)/29.88)2，深圳P(L)=0.128 8e-((L-28.66)/27.19)2，平均最短(时间)路径长度分别为38.5 min和32 min。尽管北京市轨道交通网络的覆盖范围比深圳市轨道交通网络大很多，但其平均最短(时间)路径长度仅增加6.5 min，说明北京市轨道交通网络的可达性较高。

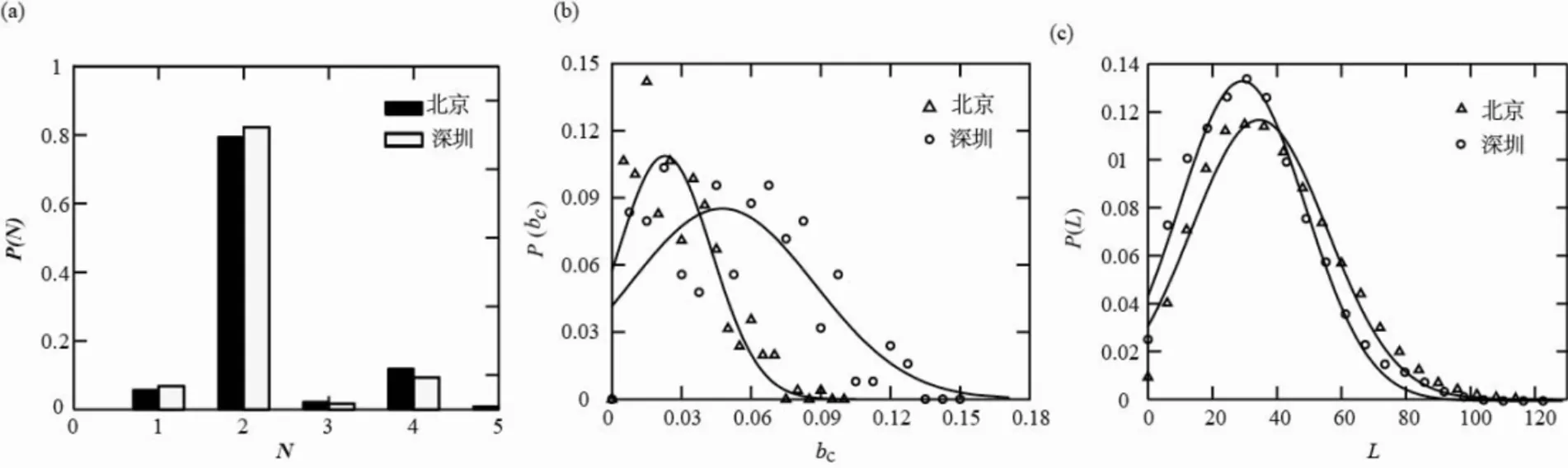
(a)节点度分布；(b)边介数中心度分布；(c)最短路径长度分布图3 轨道交通网络拓扑结构属性Fig.3 Topological properties of the urban rail transit networks

基于以上分析可知，北京市轨道交通网络的网络复杂度较高，边可替代性也较高。北京地铁和深圳地铁分别代表了轨道交通网络拓扑结构发展的两个阶段，北京市的轨道交通网络结构较为成熟，具有更强的网络可达性和连通性。

3 城市轨道交通网络的脆弱性分析

脆弱性指受事件影响而导致服务水平下降的敏感系数。在交通网络科学的相关研究中，城市轨道交通网络的脆弱性定义为不同站间区间(或站点)失效而影响轨道交通网络全局效率的大小。本文分析了城市轨道交通网络站间区间失效对乘客出行可达性及出行时间的影响。

利用Dijkstra算法,将早高峰交通需求OD按最短路径分配到轨道交通路网，统计了站间区间的客流量[16]。图4数据显示网络中的客流量分布不匀，少部分区间客流量很大，而大部分区间客流量相对较小。

3.1 出行失败率

首先，我们定义了站间区间故障导致的出行失败率fr，即轨道交通站间区间故障时，不能到达目的地的出行数占总出行数的比例，用于评估轨道交通站间区间的脆弱性(式4)。

(4)

式中:fr(v)是指站间区间v发生故障时的出行失败率；N为出行总量；ai(v)为站间区间v故障时，第i个出行是否失败，如果出行失败，则ai(v)=1，否则ai(v)=0。

图5展示了站间区间出行失败率fr的分布，两个城市轨道交通网络站间区间的出行失败率fr均服从指数分布，北京：P(fr)=0.730 4e-386.7fr(R2=0.991)，深圳：P(fr)=0.690 8e-137.8fr(R2=0.992)。出行失败率fr较高的区间均分布在地铁网络边缘，而中心环线的站间区间出行失败率偏低。造成这一现象的原因为分布在地铁网络边缘的线路多为单线路，一旦发生故障很难找到替代线路，必然导致经过此线路的出行不能完成。

虽然两个城市站间区间出行失败率分布基本一致(均服从指数分布)，但北京市轨道交通网络站间区间的平均出行失败率明显低于深圳市轨道交通网络，北京市的最高出行失败率fr只有0.04，而深圳市的最高出行失败率fr超过0.1。分析这一现象的原因是两个轨道交通网络的结构复杂度不同，北京地铁站形成的回路较多，多数出行可以找到替代线路。

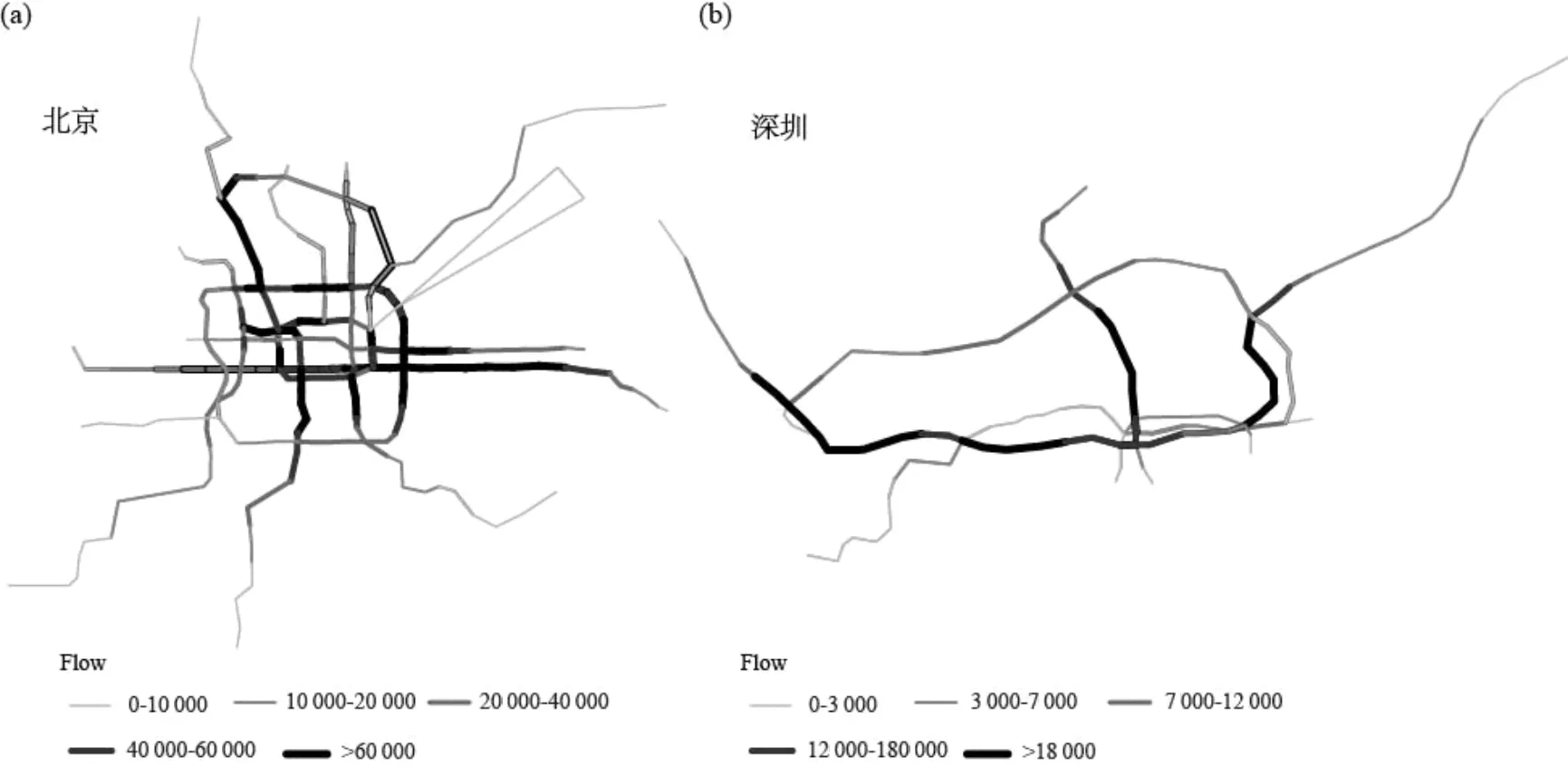
(a)北京市轨道交通客流量分布；(b)深圳市轨道交通客流量分布图4 轨道交通网络客流量分布Fig.4 Distribution of passenger flow inurban rail transit networks

3.2 出行时间增加率

拥有替代线路的站间区间一般位于环线上，当此类站间区间出现故障时，因为存在替代路径，因此出行失败率较低。但这种情况下，乘客由于需要绕路，出行时间大大增加。为了量化这一影响，我们定义了站间区间故障时造成的总出行时间增加率tr，即轨道交通发生故障时，乘客通过改变出行路径到达目的地，其增加的出行时间占总出行时间的比例(式5)。

(5)

式中：tr(v)是指站间区间v发生故障时的出行时间增加率；ti为未发生故障时第i个出行所用的出行时间；ti(v)为站间区间v发生故障时，第i个出行的出行时间。

研究发现：两个城市的轨道交通网络出行时间增加率tr较大的站间区间在空间上基本分布在环线(图5(a)和5(b))，两个城市轨道交通网络站间区间的出行时间增加率近似服从指数分布(图5(d))，北京：P(tr)=0.447 5e-214tr(R2=0.979)，深圳：P(tr)=0.512 7e-77.62tr(R2=0.965)。表明城市地铁网络站间区间发生故障时，出行时间增加率的概率分布相似。

但是，由于两个轨道交通网络的网络复杂度不同，出行时间增加量存在一定差异，深圳地铁的出行时间增加率明显高于北京地铁，北京市最大tr仅为0.059，而深圳市最大tr达到了0.24(图5(d))。即当该站间区间发生故障时，总出行时间增加24%，导致轨道交通网络效率大幅下降。

为了进一步研究城市轨道交通网络脆弱边对网络效率的影响，我们分析了脆弱边发生故障时，其它站间区间客流量的变化。选取北京市与深圳市出行时间增加率最大的站间区间，分别为北京地铁13号线知春路到五道口部分、深圳地铁罗宝线深大到桃园部分(图6)。研究发现当上述两个站间区间发生故障时，很多乘客需要选择最近环线绕行，环线客流量平均增加3倍和5倍，最大客流增加量分别为正常情况的7倍和6.6倍。

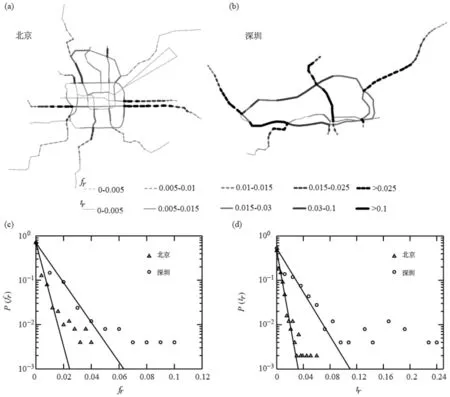
(a)北京出行失败率；(b)深圳出行失败率；(c)北京出行时间增长率；(b)深圳出行时间增长率图5 出行失败率分布与出行时间增长率分布Fig.5 Distribution of trip failure rate and distribution of trip time increasing rate

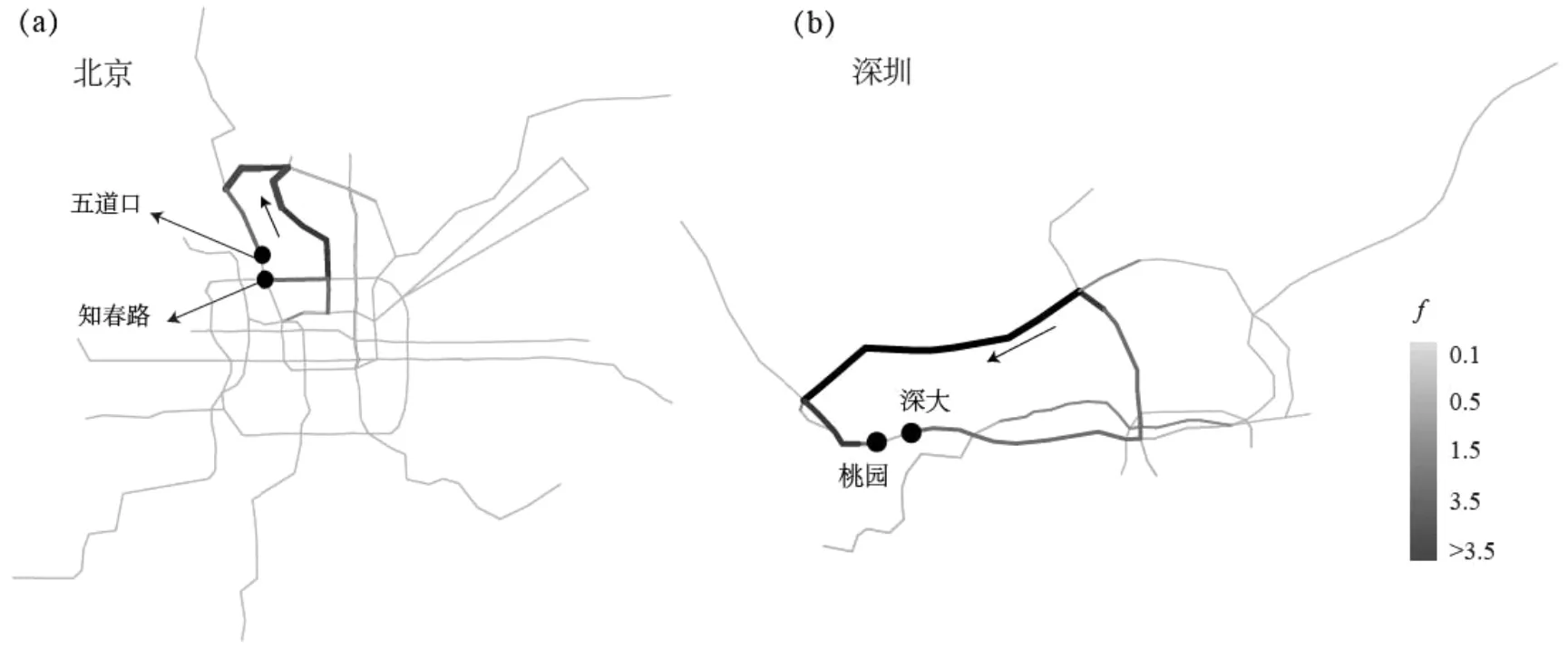
(a)北京地铁客流量增长率分布；(b)深圳地铁客流量增长率分布图6 轨道交通区间故障导致其它站间区间客流量增长Fig.6 Passenger volume increasing rate after removing the segment with largest trip time increasing rate

4 公共交通双层网络下的轨道交通网络脆弱性分析

上述研究结果表明，当城市轨道交通线路发生故障时，不仅会导致大量出行失败、总出行时间增加，还会导致某些站间区间的客流量突增。然而，上述分析结果是建立在城市仅有轨道交通网络的基础上的，实际上大城市都有比较完善的常规公交系统。为了更精确地分析轨道交通网络的脆弱性，我们以深圳为例，建立公共交通双层网络分析轨道交通故障对乘客出行带来的影响。

4.1 城市公共交通双层网络的构建

如果常规公交站点与轨道交通站点之间的距离小于500 m，则在它们之间搭建换乘边，进而构建由常规公交网络与轨道交通网络组成的城市公共交通双层网络。两层网络的换乘时间按步行时间计算，取均值为5 min。深圳市常规公交网络包含9 114个站点、17 119条边，与地铁站点距离在500 m以内的站点数量为1 197。深圳市城市公共

交通双层网络如图7所示，共包括9 232个站点，19 865条边，其中换乘边有2 394条。

图7 深圳市公共交通双层网路Fig.7 Two-layer public transportation networkof Shenzhen

4.2 城市公共交通双层网络中轨道交通路段脆弱性分析

本文依次计算了城市公共交通双层网络中每一个轨道交通站间区间发生故障时的出行失败率fr和出行时间增加率tr。考虑公交网络层后，出行失败率fr=0，平均出行时间增加率也大幅度降低，从仅考虑单层轨道交通网络时的3%降到了1.5%(图8(d))。

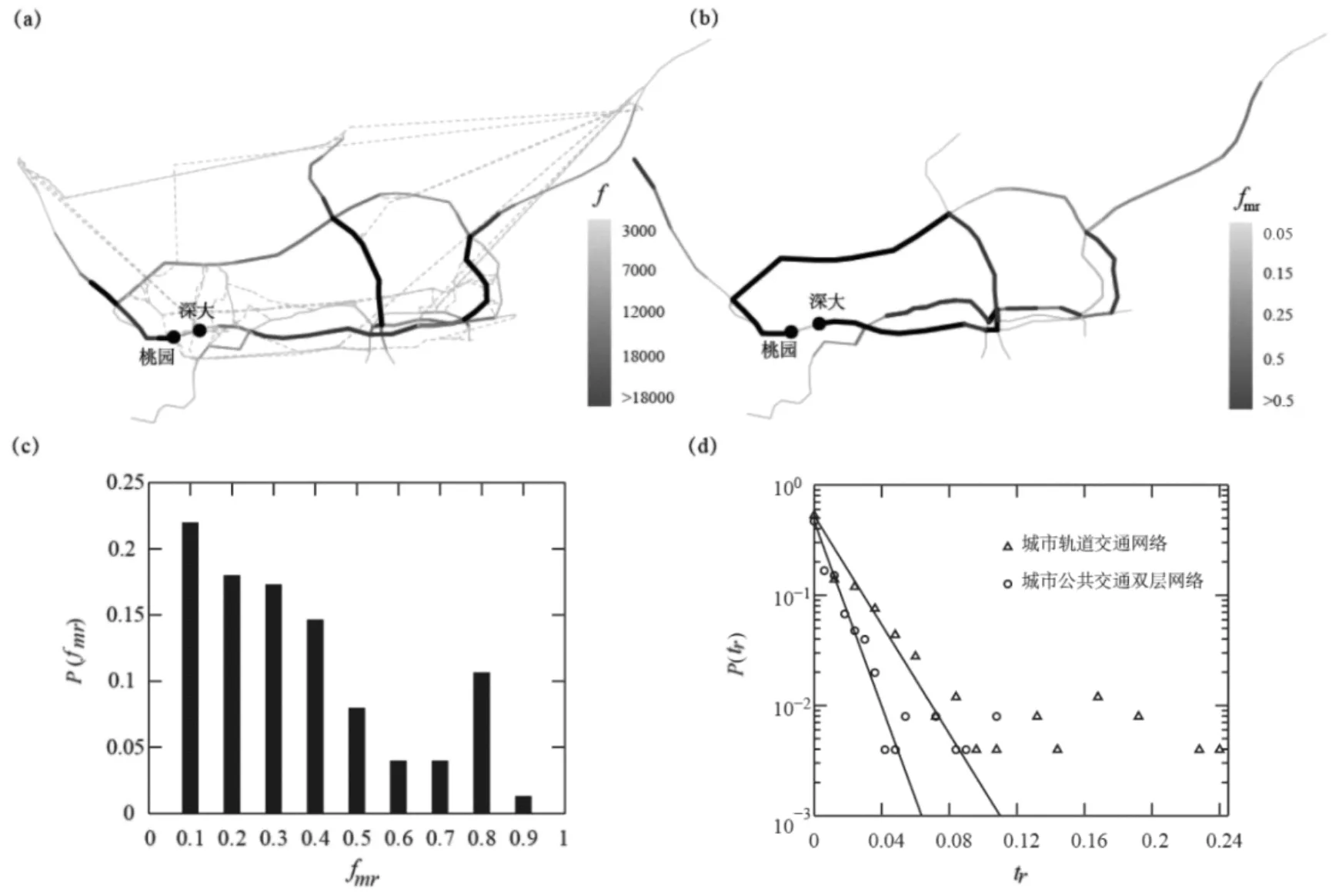
(a)流量分布；(b)、(c)流量减少分布；(d)出行时间增加率分布图8 城市公共交通双层网络流量分布，出行时间增加率分布Fig.8 Distribution of passengers volume and distribution of trip time increasing rate in Two-layer public transportation network

仍以出行时间增加率最大的深大站到桃园站区间为例，分析此站间区间故障时其它站间区间的流量变化(图8(a)和8(c))，8(a)为该区间故障时，城市公共交通双层网络中轨道交通层的客流量变化。8(b)和8(c)为该区间故障时，城市公共交通双层网络中轨道交通层比仅考虑轨道交通网络时的站间区间流量减少率fmi分布。

仿真结果表明轨道交通网络发生故障时，公交层可以分担大量流量，缓解轨道交通网络层客流量突增。轨道交通网络层的流量分布(图8(a))与未发生故障时的流量分布(图4(b))相近，乘客总出行时间仅比未发生故障时增加8.4%。而仅考虑单层城市轨道交通网络时，总出行时间增加24%。因此，常规公交网络对于降低城市轨道交通系统脆弱性具有很重要的作用。

5 结论

1)本文利用北京和深圳两个城市的大规模地铁刷卡数据，对两个轨道交通网络的脆弱性分别从出行失败率，出行时间增加率和其它站间区间客流增量三个分面做了较深入的测量和分析。研究结果表明：两城市脆弱性指标既具有相同的概率分布，又在数值上有较大差异。脆弱性的相似特征源于两城市地铁客流分布的相似性，而脆弱性的异同特征则可以从轨道交通网络的复杂度解释。

2)相比以前仅利用轨道交通网络本身分析其脆弱性，本文构建城市公共交通双层网络,考虑了常规公交对轨道交通故障的缓冲作用。我们发现常规公交网络可以在轨道交通网络发生故障时，大幅降低出行失败率和出行时间增加率，避免了轨道交通客流突增。

[1] Nguyen T P K, Bdugin J, Marais J. Method for evaluating an extended Fault Tree to analyse the dependability of complex systems: Application to a satellite-based railway system[J]. Reliability Engineering & System Safety, 2015, 133: 300-313.

[2] Cadrso L, Marín, Maróti G. Recovery of disruptions in rapid transit networks [J]. Transportation Research Part E: Logistics and Transportation Review, 2013, 53: 15-33.

[3] Vuchic V R. Urban Transit: Operations, Planning, and Economics [J]. Operations, 2005:45(:3).

[4] Derrible S, Kennedy C. The complexity and robustness of metro networks[J]. Physica A 2010, 389, 3678-3691.

[5] 韩豫, 成虎, 赵宪博, 等. 基于脆弱性的城市轨道交通运营安全理论框架[J]. 城市轨道交通研究, 2012(11):15-19. HAN Yu, CHENG Hu, ZhAO Xianbo, et al. Theoretic structure of urban mass transit operation safety based on vulnerability[J]. Urban Mass Transit. 2012(11):15-19.

[6] Angeloudis P, Fisk D. Large subway systems as complex networks [J]. Physica A: Statistical Mechanics and its Applications, 2006(367): 553-558.

[7] 邓连波, 高伟, 赖天珍, 等. 基于换乘网络的城市轨道交通关联公交接驳线网优化[J]. 铁道科学与工程学报, 2012, 9(6):77-83. DENG Lianbo, GAO Wei, LAI Tianzhen, et al. Optimal design of feeder-bus network related to urban rail transit based on transfer network [J]. Journal of Railway Science and Engineering, 2012, 9(6):77-83.

[8] 高洁, 施其洲. 城市轨道网络抗毁可靠性定义及评价指标模型研究[J]. 铁道学报, 2007, 29(3):29-33. GAO Jie, SHI Qizhou. Definition and evaluation modeling of metro network invulnerability [J]. Journal of the China Railway Society, 2007, 29(3): 005.

[9] 王志如, 李启明, 梁作论. 城市地铁网络拓扑结构脆弱性评价[J]. 中国安全科学学报, 2013, 23(8):114-119. WANG Zhiru, LI Qiming, LIANG Zuolun. Evaluation of urban metro network topological structure vulnerability[J]. China Safety Science Journal, 2013, 23(8):114-119.

[10] ZHANG Jianhua, XU Xiaoming, LIU Hong, et al. Networked analysis of the Shanghai subway network, in China [J]. Physica A: Statistical Mechanics and its Applications, 2011, 390(23): 4562-4570.

[11] SUN Jian, ZHAO Yuhan, LU Qingchang. Vulnerability analysis of urban rail transit networks: A case study of Shanghai, China [J]. Sustainability, 2015, 7(6): 6919-6936.

[12] DENG Yongliang, LI Qiming, LU Ying, et al. Topology vulnerability analysis and measure of urban metro network: The case of Nanjing [J]. Journal of Networks, 2013, 8(6): 1350-1356.

[13] HE Kun, XU Zhongzhi, WANG Pu. A hybrid routing model for mitigating congestion in networks [J]. Physica A: Statistical Mechanics and its Applications, 2015(431): 1-17.

[14] WANG Junjie, LI Yishuai, LIU Jingyu, et al. Vulnerability analysis and passenger source prediction in urban rail transit networks[J]. PloS ONE, 2013, 8(11)1-8.

[15] Newman M E J. A measure of betweenness centrality based on random walks[J]. Social Networks, 2005, 27(1): 39-54.

[16] 王俊杰, 谭倩, 王璞. 城市轨道交通客流突增研究[J]. 铁道科学与工程学报, 2015, 12(1):196-202. WANG Junjie, TAN Qian, WANG Pu. Analysis of surging passenger flow in urban rail transit network[J]. Journal of Railway Science and Engineering, 2015, 12(1):196-202.

Vulnerability analysis of urban rail transit networks

QU Yingchun, XU Zhongzhi, GONG Hang, HUANG Zhiren, WANG Pu

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

The urban rail transit network is an important part of an urban public transportation system. First, we generated the network models of the urban rail networks of Beijing and Shenzhen. We used the subway smart card data to estimate the passenger travel demands in the two urban rail transit networks. Next, we analyzed the topological structures of the two urban rail transit networks based on complex network theory and proposed the indices to evaluate the vulnerability of an urban rail transit network. Finally, we generated a two-layer public transportation network to obtain a deeper understanding of the vulnerability of urban rail transit networks. Our empirical results show that the distribution of vulnerable segments is similar in Beijing and Shenzhen rail transit networks. Averagely, Shenzhen urban rail transit network is more vulnerable. The vulnerability of an urban rail network is highly related with its network complexity. Urban bus transit network can reduce the vulnerability of urban rail transit system.

subway smart card data; urban rail transit network; OD estimation; vulnerability

2016-01-11

国家自然科学基金资助项目(61473320)

王璞(1983-)，男，河北石家庄人，教授，博士，从事交通运输规划与管理、复杂网络和数据挖掘方面的研究；E-mail: wangpu@csu.edu.cn

U231+.2

A

1672-7029(2016)11-2276-08