基于行波法的有限加肋板耦合运动研究

陈攀， 漆琼芳

(1.中国舰船研究设计中心 船舶振动噪声重点实验室， 湖北 武汉 430064; 2.武汉理工大学 交通学院， 湖北 武汉 430063)



基于行波法的有限加肋板耦合运动研究

陈攀1， 漆琼芳2

(1.中国舰船研究设计中心 船舶振动噪声重点实验室， 湖北 武汉 430064; 2.武汉理工大学 交通学院， 湖北 武汉 430063)

为研究板与加肋条的耦合运动特征，采用行波法和模态叠加法，根据板与加肋条的不同耦合连续性假设，建立3种耦合模型，即板- 附加质量模型、板- 欧拉梁模型和板- 板- 欧拉梁模型，此时3种耦合模型对应的加肋条分别为阻振质量、扁钢和T型材。根据行波法推导有限加肋板耦合结构的动力响应表达式，并自编Matlab程序进行振动响应计算，通过对比有限元数值计算结果与行波法半解析计算结果，验证该行波法解法是计算耦合结构振动响应的有效方法。对3种耦合力学模型的对比研究，根据耦合连续性假设分析结构刚度项对响应的影响，说明在低频范围内，结构刚度项对结构的动力响应影响较小，但随着频率的增大，结构刚度项对结构动力响应影响增大。对板厚和损耗因子进行参数分析，计算结果表明：随着板厚增加，板的模态数变少；在共振频率附近，随着损耗因子的增加，结构输入功率流和传递功率流的峰值降低；损耗因子的改变对结构的固有频率影响不大。

固体力学； 行波法； 有限加肋板； 功率流； 阻振质量

0 引言

舰船结构由大量梁、板和加肋板等结构组成，研究板、梁耦合系统的振动功率流可以指导舰船结构的声学设计。行波法[1](又称波动法)假定振动能量主要以弯曲波、纵向波和扭转波的形式传播，给出满足振动微分方程的解，通过简谐波叠加，根据结构的边界条件和平衡方程求取弯曲波和面内的波幅系数，最终得到振动位移响应值和结构内力。

振动功率流综合包含力与速度信息，能直观表示能量在结构中的分布与传递路径。文献[2-3]引入面内波和弯曲波，基于薄板理论控制方程，建立行波法功率流模型，得到耦合板的中、高频振动功率流分布。Tso[4]建立板- 薄梁耦合模型和板- 厚梁耦合模型，探讨弯曲波入射时入射角对弹性波的影响。Kessissoglou[5]应用行波法研究有限尺寸L型板的振动功率流，对面内波与弯曲波的功率流成分进行分析。赵芝梅等[6]采用行波法研究点力和弯矩的激励大小、激励角度和激励位置对有限L型板功率流的影响。文献[7-10]根据波动理论分析有限L型梁和有限L型板在点力激励下的主动功率流和被动功率流，并与有限元数值解进行对比，验证行波法半解析解的有效性。焦映厚等[11]建立阻振方钢与L型板的耦合运动力学模型，采用行波法分析方钢参数对振动功率流传递特性的影响。李朋洲等[12]建立平板- 阻振质量的耦合运动模型，应用波动法和模态叠加法得到结构的振动响应，分析阻振质量在低频和高频时的隔振性能。目前行波法的研究对象侧重半无限尺寸平板结构，即不考虑边界对振动波的吸收与反射半无限板。但实际舰船结构包含边界条件对弹性波的影响，因此本文行波法研究对象为有限尺寸耦合结构。

本文建立板与加肋条的3种耦合运动力学模型，即板- 附加质量模型、板- 欧拉梁模型和板- 板- 欧拉梁模型。应用行波法求解薄板理论的振动控制方程，推导3种耦合模型的行波法半解析解，自编Matlab程序进行振动响应计算，对比行波法半解析解与有限元数值解，验证行波法求解有限尺寸耦合结构的有效性。根据3种耦合模型的连续性假设，探讨结构刚度对振动传递的影响，并分析板厚和损耗因子对板梁耦合结构的振动功率流的影响。

1 行波法模型

舰船典型耦合运动结构包括：甲板- 纵骨- 横梁、船底板- 纵骨- 内底板、舷侧板- 肋骨等。建立如图1所示的板与加肋条的3种耦合运动模型： 1)当加肋条为阻振方钢，因方钢质量较大，可以假设方钢与连接线2的加速度连续，建立板- 附加质量模型；2)当加肋条为扁钢时，假设板与骨材连接处的位移连续，将骨材当成欧拉梁，建立板- 欧拉梁模型；3)当加肋条为T型材时，假定T型材腹板下端与板位移连续，T型材腹板上端与面板的速度连续，板12、板23、T型材腹板在连接线2处通过力与力矩进行耦合，加肋条面板相当于等效的力和力矩施加在T型材腹板上端，建立板- 板- 欧拉梁耦合模型。

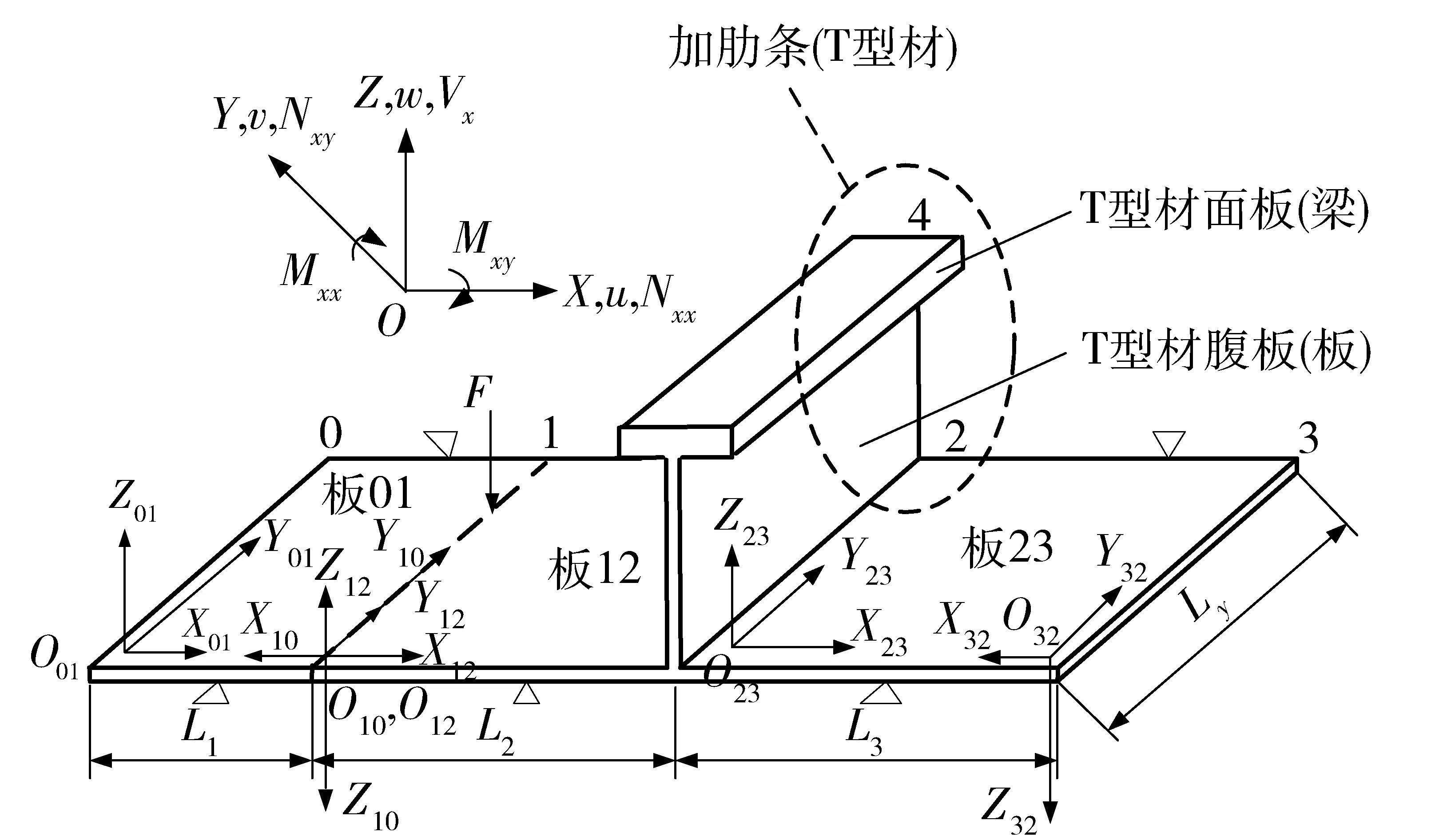
图1 板与加肋条的耦合运动模型 Fig.1 Coupled model of ribbed plate

将结构尺寸变化处、属性变化处、边界等处称作声学不连续条件，在结构的声学条件改变处将结构离散，即在点力激励处和布置加肋条位置将图1模型离散成3个板，依次为板01、板12、板23，长度分别为L1、L2、L3，板宽均为Ly.

应用Poisson-Kirchhoff薄板理论[6]，板的弯曲振动方程为

(1)

板的面内振动控制方程为

(2)

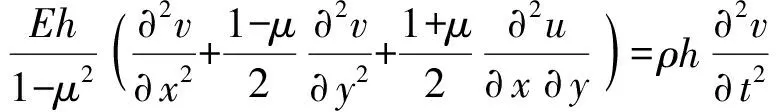
(3)

对于任意离散板，x方向的边均简支，离散板01、12、23的弯曲运动解依次为

(4)

(5)

(6)

离散板01的面内运动解：

(7)

(8)

离散板12的面内运动解：

(9)

(10)

离散板23的面内运动解：

(11)

(12)

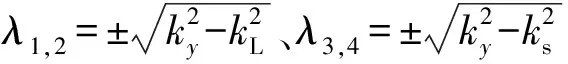
耦合力和耦合力矩与振动位移相关，表达式为

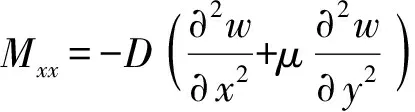
(13)

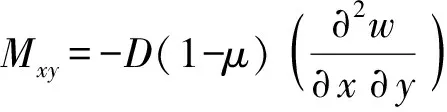
(14)

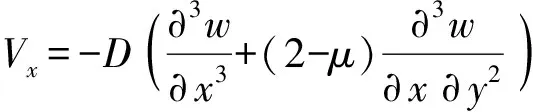
(15)

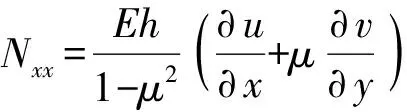
(16)

(17)

式中：Mxx、Mxy是弯矩和扭矩；Nxx、Nxy是面内纵向力和剪切力；Vx为法向纯剪力，耦合力的方向见图1.

若板01左端自由，边界条件：

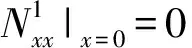
(18)

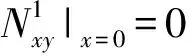
(19)

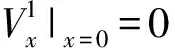
(20)

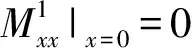
(21)

若板01右端有外界点激励作用，边界条件为

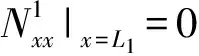
(22)

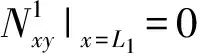
(23)

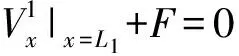
(24)

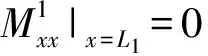
(25)

外界点力激励可以等效为线激励级数叠加：

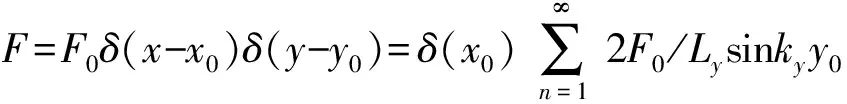
(26)

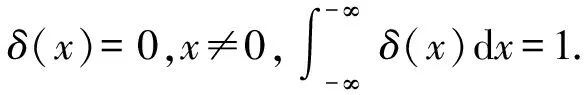
若板01与板12线连接，边界条件：

u1|x=L1=u2|x=0，

(27)

v1|x=L1=v2|x=0，

(28)

w1|x=L1=w2|x=0，

(29)

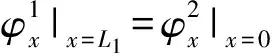
(30)

(31)

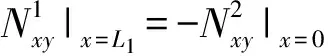
(32)

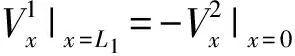
(33)

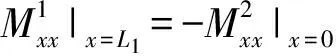
(34)

假设耦合连接2线处布置船舶结构常用的T型材，则加肋条尺寸较大，建立板- 板- 梁耦合运动模型。板01右端、板12左端、T型材腹板连接处建立力与力矩的耦合运动模型，上标f表示T型材腹板对应的位移项和力项，三者相互耦合，平衡方程为

u1|x=L1=u2|x=0=wf|x=0，

(35)

v1|x=L1=v2|x=0=vf|x=0，

(36)

w1|x=L1=-uf|x=0=w2|x=0，

(37)

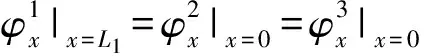
(38)

(39)

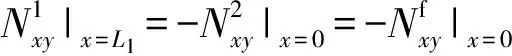
(40)

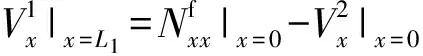
(41)

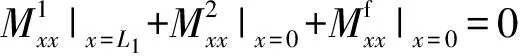
(42)

板23右端与板01左端边界条件类似，不再赘述。板与加肋条耦合处，相当于加肋条以等效的线力和力矩施加在板上，平衡方程为

NxxL-NxxR=Nxxb，

(43)

VxL-VxxR=Vxb，

(44)

MxxL-MxxR=Mxxb，

(45)

式中：NxxL、VxL、MxL、NxxR、VxR、MxR为加肋条左侧和右侧的轴向力、剪力和力矩；Nxxb、Vxb、Mxxb是加肋条施加在板上的轴向力、剪力和力矩。加肋等效成欧拉梁：

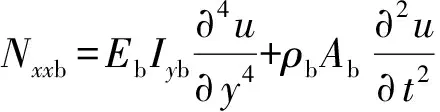
(46)

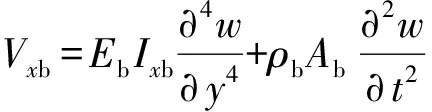
(47)

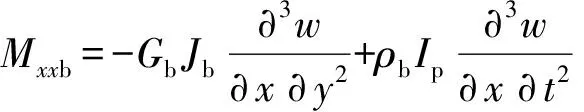
(48)

式中：ρbAb、ρbIp分别是单位长度肋条的质量和转动惯量；Ixb、Iyb分别是加肋条截面到x中性轴和y中性轴的惯性矩；Eb、Gb、ρb分别是肋条的弹性模量、剪切模量和密度；Jb为加肋条相对于截面中心的极惯性矩。

假设耦合连接线2处布置阻振方钢，因阻振方钢质量较大，布置方钢相当于板上施加质量体，在耦合连接处，方钢与板连接处的加速度连续，布置方钢相当于在连接处施加附加力和力矩，方钢的力与位移满足：

(49)

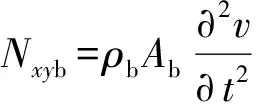
(50)

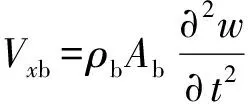
(51)

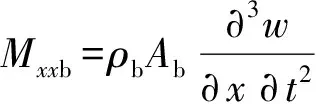
(52)

则

kyB3eλ3x+kyB4eλ4x)sin(kyy),

(53)

A3e-knx+A1eknx)sin (kyy),

(54)

jksxA2e-jksx-knA3e-knx+knA4eknx).

(55)

2 振动功率流

不同于有限元法用1/3倍频程结构导纳和振级落差来评价隔振性能，行波法可以采用功率流来度量振动传递能量。单位时间流过垂直于波传播方向单位面积的振动能量称为振动功率流，行波法求出某一截面、某一点在频域范围内的振动功率流后，进而可以求出平板的平均振动功率流，在频域范围内对功率流进行积分可以求出整个平板的功率流，薄板理论的功率流表达式为

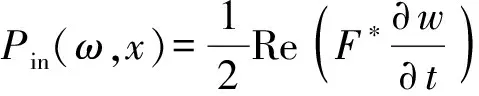
(56)

(57)

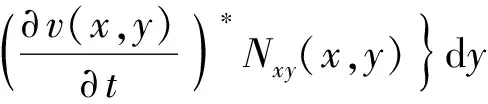
(58)

Ptot(ω,x)=Pm(ω,x)+Pb(ω,x)，

(59)

式中：上标*表示共轭复数；Pin是点激励的输入功率；Pb和Pm分别是弯曲波功率流和面内波功率流；Ptot是面内波功率流与弯曲波功率流总和。

3 计算模型

自编计算模型的振动响应行波法程序，假定板长L1=L2=L3=0.6 m，板宽Ly=0.6 m，板厚h=0.01 m，弹性模量E=2.0×1011Pa，考虑材料的能量损耗的复弹性模量为Ep=E(1+jη)，结构阻尼η=0.01，材料泊松比μ=0.3，密度ρ=7 800 kg/m3. 板的横向载荷为F=F0eiωt，位于板1右端中点，力的幅值F0=1 N. 应用行波法进行Matlab编程计算，得到每个点位移和内力响应的行波法解析解，根据内力和位移及频率关系即可得到响应点的功率流，对某一截面积分即可得到该截面的功率流。采用数值方法计算对应模型振动响应，在有限元软件ABAQUS里建立三维模型，划分网格并进行数值计算，有限元的网格尺寸为0.02 m×0.02 m，如板23的尺寸为0.6 m×0.6 m，相应的有限单元数目为30×30.

3.1 行波法解析解的有效性验证

将图1加肋板结构离散，离散板01、12、23通过线连接，激励位于板01右端中点，观测点位于板23中点。在0～800 Hz计算频率范围内，图2显示了平板的有限元数值解与行波法解析解，对比横向位移曲线可知，在低于500 Hz的频率范围内两种曲线吻合较好，随着频率的增加，两种方法的计算结果出现一定差别，主要原因：1)有限元法的网格密度有关影响计算结果精度，网格不同，结果会出现差异；2)有限元法具有高频不稳定性，高频不易收敛。图2的响应曲线吻合较好，验证行波法公式推导的正确性，证明行波法是求解耦合结构的稳态响应的一种有效方法。

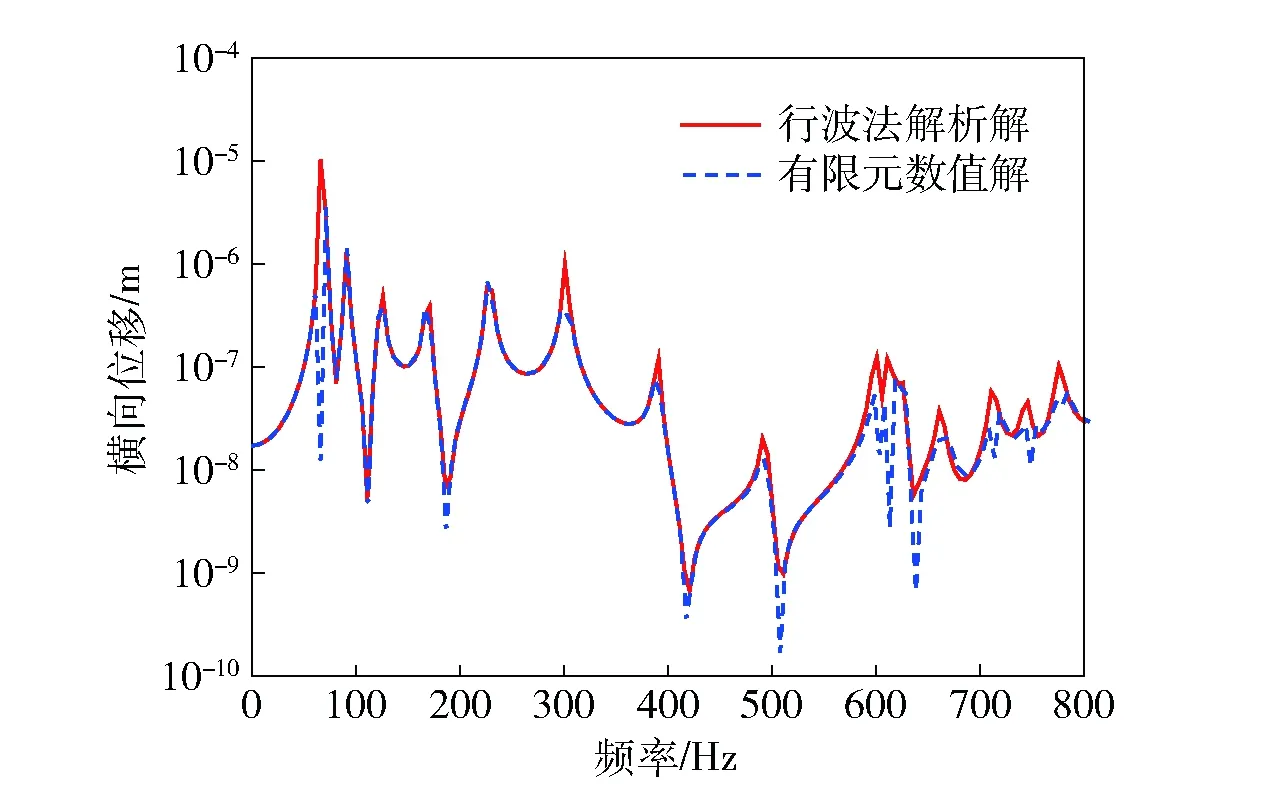
图2 平板模型的横向位移Fig.2 Z-direction displacement of plate model

假设在图1模型的连接线上布置骨材，骨材是截面尺寸为0.06 m×0.06 m的扁钢，建立平板与骨材的板- 欧拉梁耦合运动模型，板一对边简支，一对边自由。观测点在激励位置处，图3中有限元数值解与行波解求出的稳态响应曲线吻合较好，验证行波法求解板- 欧拉梁模型的有效性。

图3 板- 欧拉梁耦合模型的横向位移Fig.3 Z-direction displacement of plate-Euler beam coupling model

3.2 加肋板3种耦合运动模型

建立如图1所示模型，在离散板01右端施加点力激励，在离散板12与离散板23连接处布置加肋条，如骨材或方钢，加肋条的截面尺寸为0.02 m×0.02 m，加肋条材料参数与板相同。板上布置肋条相当于板上施加附加质量和附加惯性矩，分为3种耦合情况：板- 欧拉梁模型、板- 附加质量模型和板- 板- 欧拉梁模型。通过3种耦合模型的行波法Matlab程序计算点激励位置处的稳态响应曲线。

由图4可知，在小于1 000 Hz的频率范围内，板- 欧拉梁模型和板- 附加质量模型的横向位移曲线接近，大于1 000 Hz频率，频响曲线的相位和峰值会出现差别。分析两种耦合模型的振动控制方程，板- 欧拉梁耦合模型比板- 附加质量耦合模型多出了结构刚度项，可知在低频范围内，刚度项对结构的动力响应影响较小，随着频率的增大，结构的刚度项对结构动力响应影响增大。

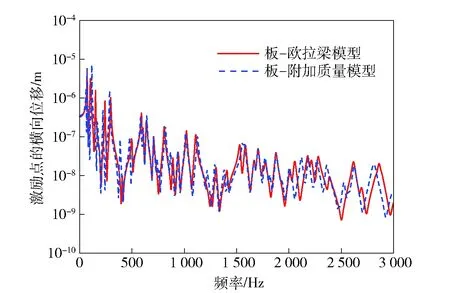
图4 两种加肋板耦合模型的横向位移Fig.4 Z-direction displacements of two coupling models

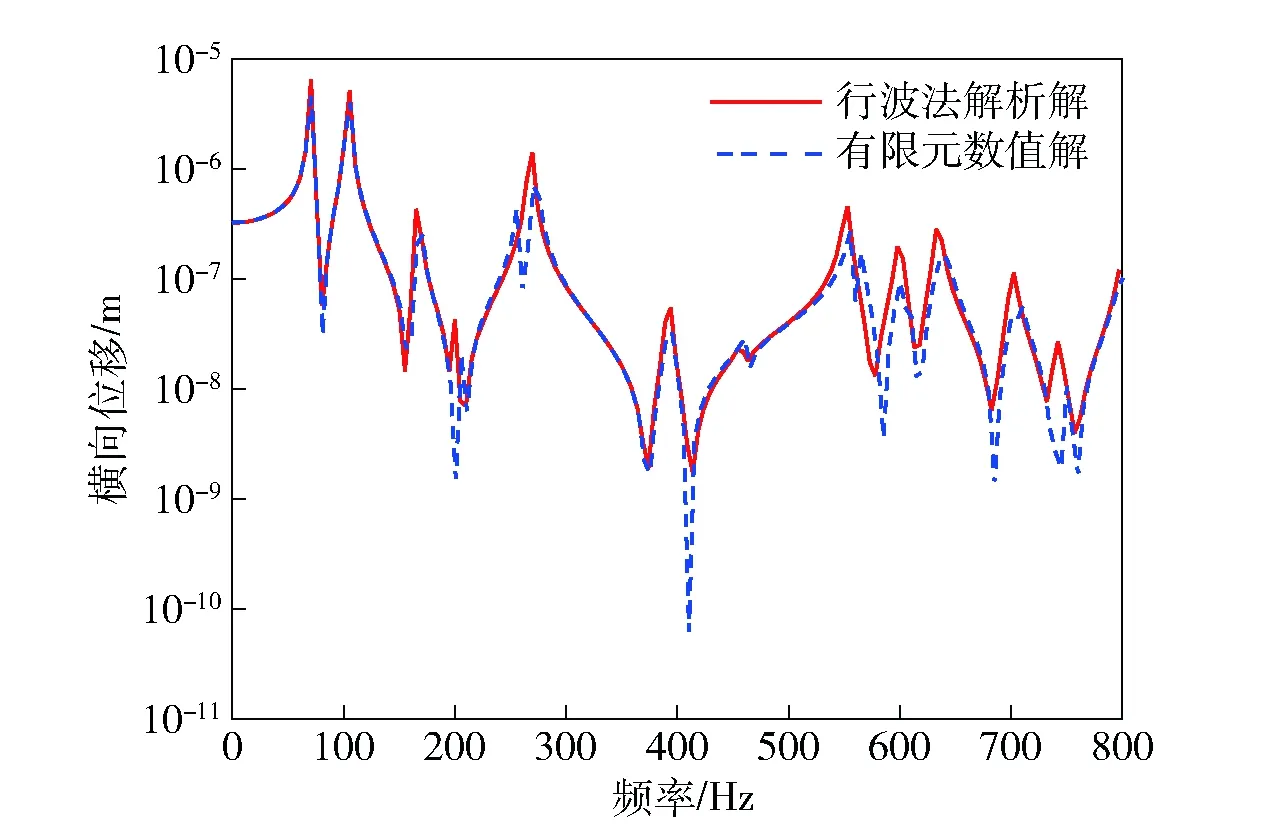
图5 板- 板- 欧拉梁耦合模型的横向位移Fig.5 Z-direction displacement of coupling model of plate-plate-Euler beam

若连接线2上布置T型材，把T型板的腹板当板属性考虑，尺寸为0.2 m×0.2 m，面板当欧拉梁属性考虑，尺寸为0.04 m×0.04 m，建立板- 板- 欧拉梁耦合运动模型。观测点在激励位置处，在计算频率1～1 000 Hz范围内，图5显示了有限元数值计算方法与行波法计算方法的横向位移曲线，对比可知，在小于400 Hz的低频范围内，两种耦合模型的计算结果吻合较好，随着计算频率的增加，曲线的峰值和相位会出现一定差异。这是因为随着频率的增加，板和梁对振动波传递会表现出差别。在实际工程中对船舶结构的加筋板进行振动分析时，一般采用通用的有限元商业软件进行振动计算，应用有限元建立三维模型建时，把肋板当成板单元或梁单元计算时，数值结果会出现差别，是由板和梁对振动波的传递特性不一致导致。行波法是基于理论公式的推导一种半解析方法，使振动波具有明确的物理意义，是振动波传递特性研究的一种有效的解析方法。

3.3 分析结构参数对功率流影响

图1模型不布置加肋条，板的结构阻尼均为η=0.01，仅考虑光板的振动传递特性，板宽Ly=0.4 m，步长取5 Hz，板长等其他参数与3.1节一致。假定平板一对边简单支撑，另一对边自由。图6显示了平板厚度变化时的输入功率流，图7显示了平板厚度变化时的传递功率流。对比可知，随着板厚增加，在计算频率范围内，输入功率流曲线和传递功率流曲线的峰值密度减少。这是因为随着板厚的增加，在分析频域内板模态数变少，所以在船体结构设计时要充分考虑板厚对模态振动影响，以免激起模态振动，使振动功率流曲线过度密集。

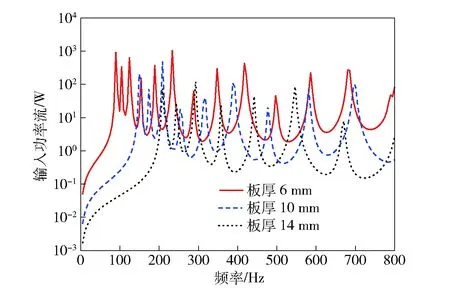
图6 不同板厚时的输入功率流Fig.6 Input power flows of plates with different thicknesses

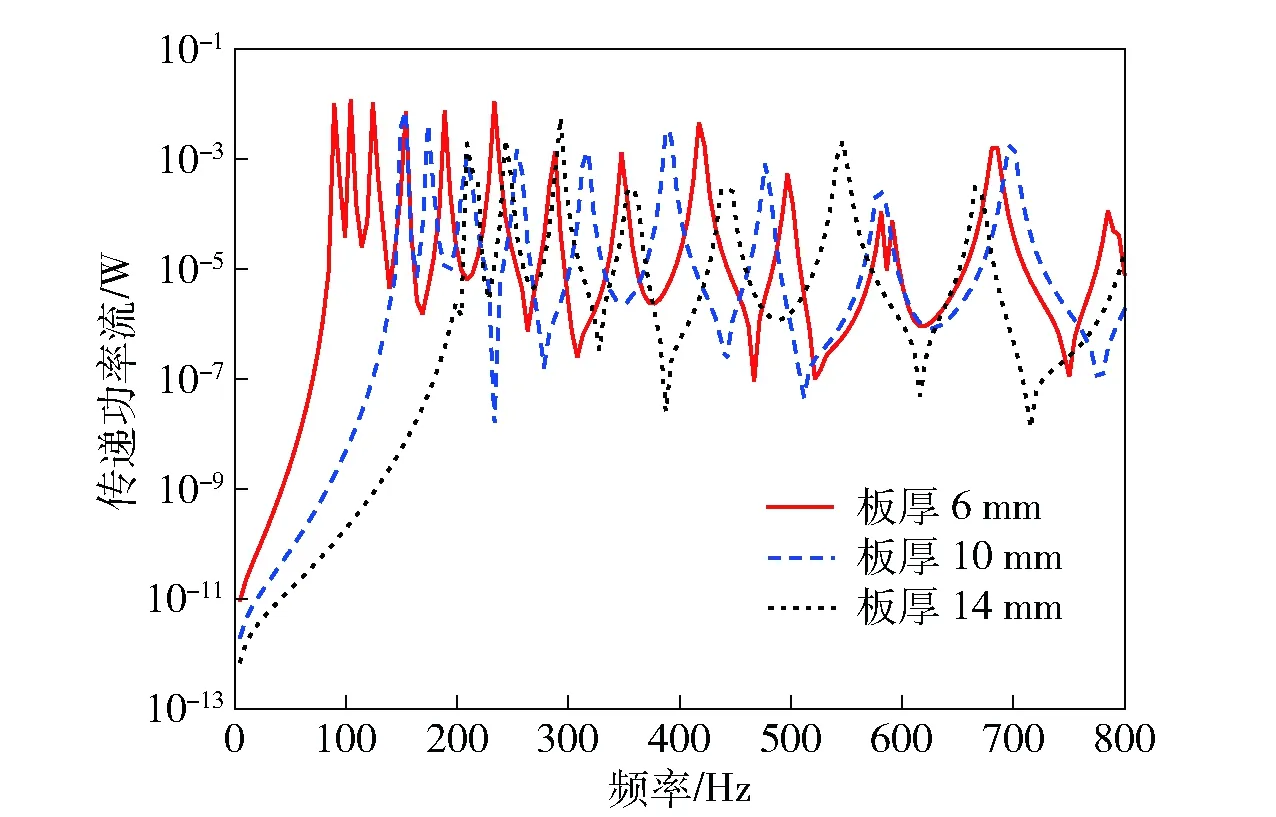
图7 不同板厚时的传递功率流Fig.7 Transmitted power flows of plates with different thicknesses

图1模型布置加肋条，尺寸为0.02 m×0.02 m，尺寸参数与3.1节一致，板一对边简支，另一对边自由。损耗因子表示成板损耗因子/加肋条损耗因子的形式，选用板- 欧拉梁耦合模型。在0～1 000 Hz计算频率范围内，图8显示了不同损耗因子比的输入功率流，图9显示了不同损耗因子比的传递功率流，对比可知，功率流曲线峰值窄而陡，对应的频率范围较窄。可知在共振峰值附近，随着板结构损耗因子的增加，输入功率流曲线和传递功率流曲线的峰值降低，功率流曲线峰值和低谷的幅度下降。在非共振峰值附近的计算频域内，随着板损耗因子的增加，输入功率流和传递功率流均增加。

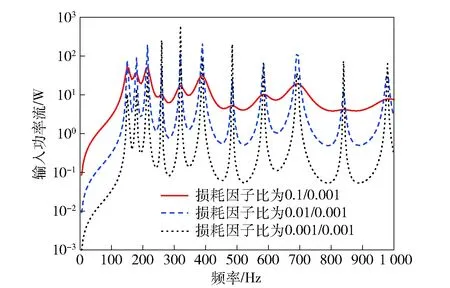
图8 0～1 000 Hz频率范围内的输入功率Fig.8 Input power flows in frequency range of 0～1 000 Hz

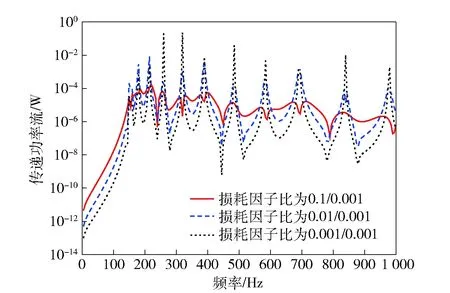
图9 0～1 000 Hz频率范围内的传递功率Fig.9 Transmitted power flows in frequency range of 0～1 000 Hz

在1 000～4 000 Hz计算频率范围内，由图10可知，板的输入功率流曲线峰值和低谷相比与低频阶段更加密集，共振频率更加密集。随着板损耗因子的增加，功率流曲线相比低频阶段没有明显的峰值和低谷，曲线更加趋于平缓，说明板损耗因子可以改变功率流曲线的峰值和低谷。根据离散板23的传递功率曲线可知，板损耗因子η=0.1且梁损耗因子η=0.001时，输入功率流曲线较为平缓(见图10)，而传递功率流曲线会出现低谷(见图11)，功率流低谷的出现与欧拉梁计算频段内振动波的阻抑有关。

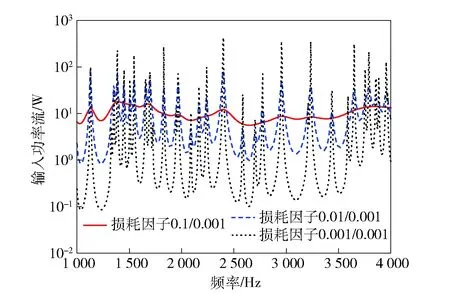
图10 1 000～4 000 Hz时的输入功率Fig.10 Input power flows in frequency range of 1 000～4 000 Hz

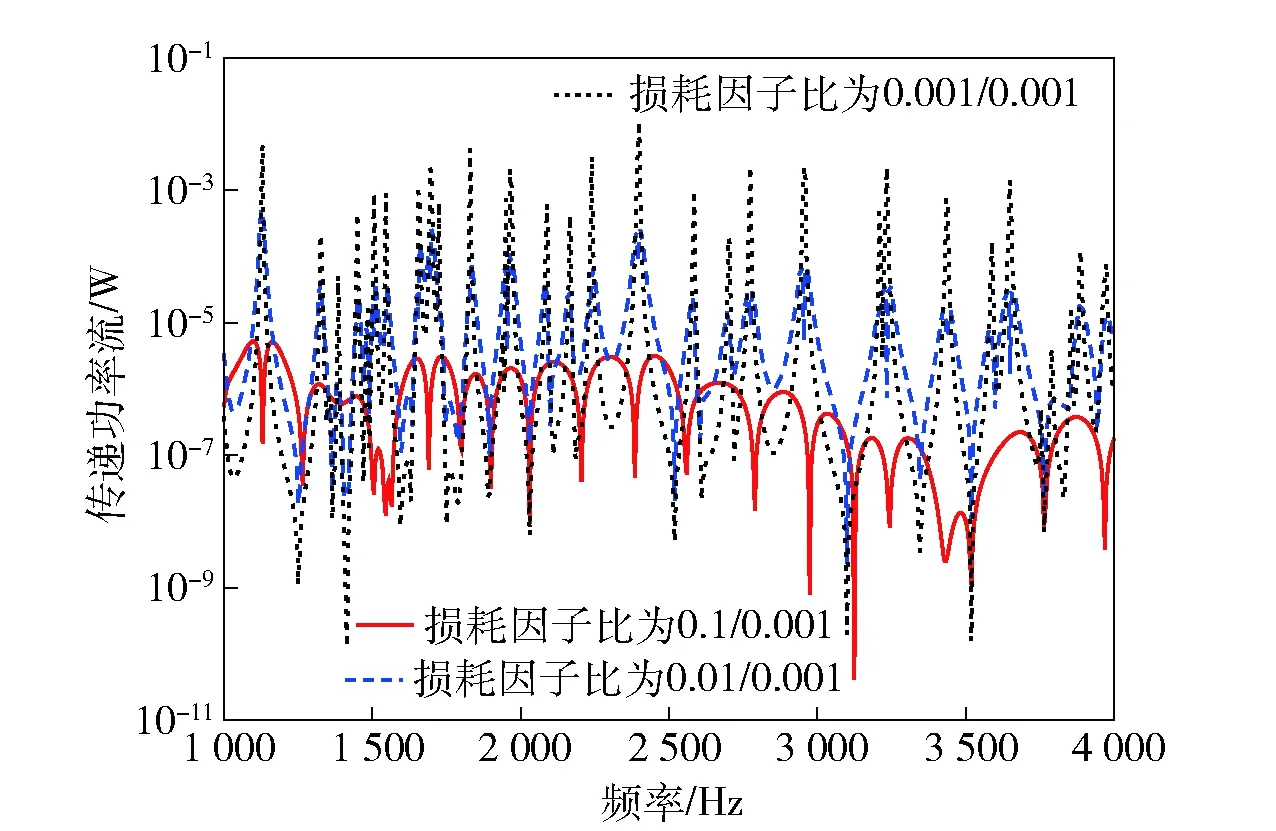
图11 1 000～4 000 Hz时的传递功率Fig.11 Transmitted power flows in frequency range of 1 000～4 000 Hz

以上结果表明在船舶减振设计时，增加板的损耗因子的可以有效减少振动能量传递和振动能量峰值。随着频率的增加，板的输入功率流可趋近于平缓，这是由于加肋条对某些频段内的振动波的阻抑作用。损耗因子改变时，输入功率流和传递功率流的峰值位置改变很小，这说明损耗因子对结构的固有频率影响很小，在船舶声学设计时，若通过改变结构损耗因子的方法改变结构的固有频率，以错开共振频率范围，则达不到应有的减振效果。

4 结论

根据板与加肋条的3种耦合连续性假设，建立板- 加肋条的3种力学模型，应用行波法和模态叠加法推导结构振动响应公式，自编Matlab程序计算耦合结构振动响应，采用有限元数值计算结果验证行波法解析计算结果的可靠性，对输入功率流和传递功率流进行参数分析，通过计算分析总结如下：

1)行波法半解析解法可以有效地计算板- 附加质量模型、板- 欧拉梁模型和板- 板- 欧拉梁模型的动力响应和振动功率流，是一种分析耦合结构振动特性的有效方法。对比板- 欧拉梁耦合模型和板- 附加质量耦合模型的振动响应曲线，说明加肋板刚度项对结构动力响应的影响会随着频率的增加而变大。

2)结构损耗因子的改变对振动功率流曲线的相位影响较小，所以损耗因子对结构固有频率影响很小。因此在进行舰船结构振动噪声危害治理时，若期望将结构的固有频率与螺旋桨激励频率错开以减少共振，仅通过施加阻尼材料产生的效果不大。

3)在共振频率附近，损耗因子的增加可以减少输入功率和传递功率的峰值。随着频率的增加，板- 欧拉梁耦合模型的传递功率流曲线会出现低谷。因此在船体结构声学设计时，可以通过增加损耗因子来改变共振频率附近的振动传递能量分布幅值，通过布置加肋条可以抑制特定频段内的振动传递能量。

References)

[1] 阿·斯·尼基福罗夫. 船体结构声学设计[M]. 谢信, 王轲,译. 北京:国防工业出版社, 1998. Никифоров А С. Acoustic design of hull structure[M]. XIE Xin, WANG Ke, transtated. Beijing: National Defense Industry Press, 1998. (in Chinese)

[2] Park D H, Hong S Y, Kil H G, et al. Power flow models and analysis of in-plane waves in finite coupled thin plates[J]. Journal of Sound and Vibration, 2001, 244(4):651-668.

[3] Park Y H, Hong S Y. Vibrational power flow models for transversely vibrating finite Mindlin plate[J]. Journal of Sound and Vibration, 2008, 317(3):800-840.

[4] Tso Y K. The evaluation of transmission efficiency and coupling loss factor of structural junctions[R]. Ascot Vale, Victoria, Australia: Materials Research Labs, 1993.

[5] Kessissoglou N J. Power transmission in L-shaped plates including flexural and in-plane vibration[J]. Journal of the Acoustical Society of America, 2004, 115(3):1157-1169.

[6] 赵芝梅, 盛美萍. 激励特性对L型板振动功率流的影响[J]. 兵工学报, 2013, 34(8): 986-993. ZHAO Zhi-mei, SHENG Mei-ping. Effect of driving force characteristics on the power flow of L-shaped plate[J]. Acta Armamentarii, 2013, 34(8): 986-993.(in Chinese)

[7] Liu C C, Li F M, Liang T W, et al. The wave and vibratory power transmission in a finite L-shaped Mindlin plate with two simply supported opposite edges[J]. Acta Mechanica Sinica, 2011, 27(5):785-795.

[8] Liu C C, Li F M, Huang W H. Active vibration control of finite L-shaped beam with travelling wave approach[J]. Acta Mechanica Solida Sinica, 2010, 23(5): 377-385.

[9] Liu C C, Li F M, Fang B, et al. Active control of power flow transmission in finite connected plate[J]. Journal of Sound and Vibration, 2010, 329(20): 4124-4135.

[10] Li F, Liu C C, Liang T. Analysis and experiment on transient dynamic response in finiteMindlin plate[J]. Acta Mechanica Solida Sinica, 2013, 26(2): 129-139.

[11] 焦映厚, 侯守武, 陈照波, 等. 采用波动法研究有限尺寸加肋 L 型板结构的振动特性[J]. 振动工程学报, 2013, 26(6): 871-878. JIAO Ying-hou, HOU Shou-wu, CHEN Zhao-bo, et al. Research on vibration properties of finite rib-stiffened L-shaped plate using wave method[J]. Journal of Vibration Engineering, 2013, 26(6): 871-878.(in Chinese)

[12] 李朋洲, 卢军, 孙磊. 阻振质量对有限平板振动传递影响分析[J]. 核动力工程, 2014, 35(1): 78-81. LI Peng-zhou, LU Jun, SUN Lei. Effect analysis of vibration transmission of finite plate with blocking mass[J]. Nuclear Power Engineering, 2014, 35(1): 78-81. (in Chinese)

Coupled Motion Analysis of Finite Ribbed Plate Based on Traveling Wave Approach

CHEN Pan1， QI Qiong-fang2

(1.National Key Laboratory on Ship Vibration & Noise, China Ship Development and Design Center, Wuhan 430064, Hubei, China; 2.School of Transportation, Wuhan University of Technology, Wuhan 430063, Hubei, China)

Traveling wave method and modal superposition method are used to study the coupled motion characteristics of plate and added ribs. According to the coupled continuity hypothesis of plate and rib, three kinds of coupling model, i.e., plate-additional mass model, plate-Euler beam model and plate-plate-Euler beam model, are established. The three coupling models correspond to blocking mass, flat steel and T-shaped plate, respectively. The dynamic response of finite plate is derived based on the traveling wave method. A self-compiled Matlab program is applied to calculate the vibratory response. The traveling wave method is verified to be an effective approach to calculate the coupled structure by comparing the numerical result of the finite element method with the calculated result of the traveling wave method. The coupling models with three different ribs are compared and analyzed. According coupled continuity assumption, the effect of structural rigidity on response is investigated. In low frequency range, the structural stiffness has less effect on dynamic response. As frequency increases, the impact of structural stiffness on dynamic response increases. The impacts of thickness and loss factor on vibration are analyzed. The results show that, with the increase in plate thickness, the modal number of plate is reduced. In the nearby regions of the resonant frequencies, the peaks of input power and transmission power are decreased with the increase in loss factor. The loss factor has less effect on the natural frequency of structure.

solid mechanics; travelling wave method; finite ribbed plate; power flow; blocking mass

2015-11-16

国家自然科学基金项目(51409238)

陈攀(1989—)，男，工程师。E-mail:panda3267@126.com

U661.44

A

1000-1093(2016)11-2128-08

10.3969/j.issn.1000-1093.2016.11.022