可修单元组合任务维修度评估方法研究

韩小孩， 张耀辉， 王少华， 曹兴伟

(1.装甲兵工程学院 技术保障工程系， 北京 100072； 2.总参谋部 工程兵科研三所， 河南 洛阳 471023)



可修单元组合任务维修度评估方法研究

韩小孩1， 张耀辉1， 王少华1， 曹兴伟2

(1.装甲兵工程学院 技术保障工程系， 北京 100072； 2.总参谋部 工程兵科研三所， 河南 洛阳 471023)

针对传统任务维修性评估方法不能有效估算特定任务剖面内装备总体维修时间问题，提出一种可修单元组合任务维修度评估方法。采用贝叶斯更新理论对功能单元维修时间概率密度函数进行更新；通过仿真加拟合的方式对可修单元组合各故障事件排除概率进行计算。示例分析表明：该方法不仅能解决因数据不完全统计因素引发的功能单元概率密度函数估计不准确的问题，而且能更加便捷地计算多个函数的卷积；任务维修度评估结果更加可信。

兵器科学与技术； 可修单元组合； 任务维修度； 贝叶斯更新； 故障事件

0 引言

维修性是指产品在规定的条件下和规定的时间内，按规定的程序和方法进行维修时，保持或恢复到规定状态的能力[1]。装备的维修性主要反映特定维修约束条件下，给定装备故障的排除难易程度。正确评估装备维修性有利于合理制定维修计划。作为维修性的一个特例，任务维修性主要反映装备在执行任务过程中发生故障，经维修恢复到规定功能的能力。其衡量指标主要有：任务维修度、恢复功能的任务时间、平均停机时间等。合理地评估装备任务维修性是正确评估任务成功性的基础，也是实施基于任务维修决策的基本前提。

任务维修度是指在任务剖面内任务功能单元发生故障，经维修恢复至规定功能时所消耗时间小于规定时间的概率。与恢复功能的任务时间相同，其实质都是评估装备的维修时间。因此，现有研究大多致力于维修时间的估算上。如文献[2]针对传统平均修复时间评估中存在的样本数据局部抽样问题和实验数据与现场数据混用的问题，分别提出了基于Bootstrap和基于证据理论的平均修复时间评估模型；文献[3]将环境因素的影响考虑到维修度计算中，提出了比例维修模型；文献[4]综合考虑了时变因素与非时变因素对维修时间的影响，提出了改进比例维修模型，实现了维修度精确评估；文献[5]建立了维修时间与维修工时模型，分别用维修活动总时间和维修工时两个参数评估了系统的维修性；文献[6]基于蒙特卡洛算法，研究了导弹营任务维修性的仿真算法；文献[7]建立了一种基于M/G/1可修排队模型的武器系统平均修复时间模型，并给出了定量预计方法；文献[8]应用Petri网技术在Expects仿真环境下建立了机动防空任务聚合级装备作战单元维修性仿真模型；文献[9]将装备各维修活动时间进一步分为共同维修时间(主要包括准备时间、接近时间和再组装时间)和个体维修时间，为精确评估任务维修性打下了基础；文献[10]构建了基于着色随机时间Petri网的维修过程模型，在此模型基础上利用蒙特卡洛算法，实现了维修时间的仿真；文献[11]利用维修性模型框图分析了单元维修时间已知情况下混联系统的维修时间。总体来看，目前研究多集中在单个单元的维修时间估算上，很少研究特定任务剖面内为维持装备处于正常状态所需的总体维修时间估算问题。尽管文献[11]对系统的维修时间进行了分析，但是在分析过程中假设各单元的维修时间已知。然而，各单元维修时间并不是一个精确的数值，据此无法准确估算系统维修时间。

实际上，在一个任务剖面内的不同时间点装备各功能单元故障是随机发生的，从而使得整个任务剖面内可能有多个可修单元发生故障。此时，维修者需要在规定时间内依次完成多个单元的维修工作，各单元的允许维修时间并不确定。因此，无法分别对各单元任务维修度进行评估，只能对任务剖面内所有可能发生故障可修单元组合的任务维修度进行评估。此外，由于可修单元维修时间通常为服从某一分布的随机变量，有必要研究各单元的维修时间分布，从而利用各单元维修时间概率密度函数进行多个可修单元组合的任务维修度评估。

基于这一考虑，本文主要研究装备执行任务过程中可修单元组合任务维修度评估问题。利用组合事件后验概率计算原理建立可修单元组合任务维修度评估模型，利用贝叶斯更新理论估计各功能单元维修时间概率密度函数，利用仿真加拟合的方式对可修单元组合各故障事件排除概率进行计算。

1 可修单元组合任务维修度评估模型

针对任务进行装备维修时，对于那些与执行任务无关的功能单元，即使在任务中发生故障也不影响任务的执行，通常等到任务结束后再进行维修。而对于那些可影响任务的功能单元，可根据其在任务过程中的可修性可分为可修单元和不可修单元。其中，不可修单元一旦发生故障无法实施任何修复措施(维修或更换)，其任务维修度可认为是0. 而对于可修单元，只有在任务中将所有发生故障的可修单元均修复才能保证任务继续执行。实际上，装备所有可修单元可组合成一个可修单元组合。该组合在任务过程中的任务维修度可反映装备在任务过程中的整体维修水平。

在任务过程中，若某几个单元同时发生故障时方可影响任务(任务成功或失败)，则认为这几个单元之间在功能上存在“并联关系”。将存在“并联关系”的多个单元视作一个整体，为保障任务的时效性，在任务过程中该整体发生故障(各单元均故障)后仅对维修时间消耗最小的单元进行维修。同理，在构建可修单元组合时，将存在“并联关系”的功能单元均视作一个整体，从而使得可修单元组合成为一个纯串联系统。由于篇幅有限，本文不对“并联关系”进行过多讨论。

假设：某装备执行某项任务时共有n个可修单元(串联关系)，a1,a2,…,an.E为n个可修单元组成的可修单元组合，T为任务中允许的最大维修时间。可知，E发生故障的概率等于a1,a2,…,an中至少有一个发生故障的概率。E发生故障后在时间T内可修复的概率为E的任务维修度。

令各单元在任务过程中发生故障的概率分别为p(a1),p(a2),…,p(an)；维修时间概率密度函数分别为ma1(t),ma2(t),…,man(t). 如果把n个单元的每一种故障组合(各组合事件之间互斥)称为E的一个故障事件，则E共有2n-1个可能的故障事件，其中第i个故障事件记作Ei. 可知，可修单元组合E发生故障的概率为

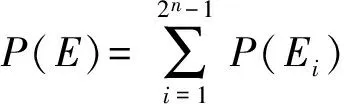
(1)

式中：P(Ei)为故障事件Ei发生的概率。例如，假设故障事件Ei为第j个与第k个单元发生故障，其余单元不发生故障，则Ei发生的概率为

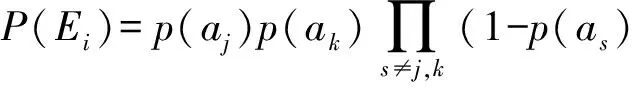
(2)

故障事件Ei发生后在T内被排除的概率为

M(Ei)=P(Tj+Tk≤T),

(3)

式中:Tj、Tk分别代表第j个与第k个单元发生故障后的维修时间消耗；P(Tj+Tk≤T)取值与maj(t)、mak(t)相关。

根据后验概率计算原理可得可修单元组合E的任务维修度为

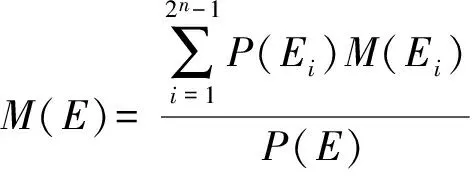
(4)

在进行可修单元组合任务维修度评估时需解决以下3个关键问题：

1)各可修单元发生故障的概率p(ai)(i=1,2,…,n)的评估问题。此问题目前研究较多，可依据已知故障规律仿真计算[12]，也可结合任务前后单元技术状态进行计算[13]。由于篇幅有限，此处不加赘述。

2)各可修单元维修时间概率密度函数mai(t)(i=1,2,…,n)的估计问题。具体论述可见本文第2节。

3)可修单元组合各故障事件排除概率P(Ei)(i=1,2,…,2n-1)的计算问题。此问题将于本文第3节讨论。

2 基于贝叶斯更新的可修单元维修时间概率密度函数估计

在日常维修工作中，因装备的损坏程度和故障性质不同，相同约束条件下维修时间一般服从某一概率分布。因此，有必要对功能单元维修时间概率密度函数进行估计。针对这一问题，传统做法一般利用已知的一系列维修时间数据直接估计概率密度函数中各参数。这一作法可较为便捷地估计出各参数，但是在计算时要求已知数据能够较大程度上反映分布特征，对于不完全统计数据或新装备统计数据较少时，评估精度较低。实际上，同类功能单元的维修水平通常是固定的，这就使得隶属于不同装备(类似装备)同类功能单元的维修时间也相近，即存在大量的先验知识。为减小数据不完全统计或数据过少带来的误差，本文结合先验知识采用贝叶斯更新理论对维修时间概率密度函数进行更新。较之传统估计方法，贝叶斯更新理论可有效融合先验知识与现有数据，评估精度较高[14-15]。

2.1 贝叶斯更新基本原理

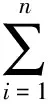
h(X,θ)=p(X|θ)π(θ).

(5)

利用贝叶斯后验概率计算原理，可得θ的后验概率密度函数为

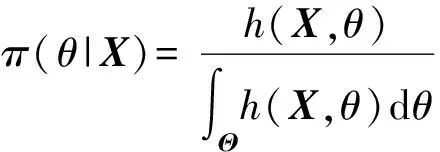
(6)

在实际工作中，人们更期望获得一个固定的θ值。因此，需要利用后验概率分布对θ进行估计。常用估计方法主要有最大后验估计、后验中位估计和后验期望估计3类[16]。其中，后验期望估计也称为贝叶斯估计，是最常用的一种参数估计方法。利用后验期望估计方法获取的θ估计值记作：

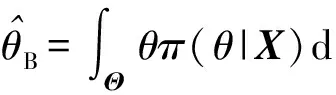
(7)

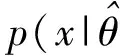
2.2 可修单元维修时间概率密度函数估计

就目前统计情况来看，功能单元维修时间一般服从正态分布、对数正态分布或指数分布中的一种。通常情况下，对于故障简单、单一的功能单元，维修时间服从正态分布；对于修理频率和修理持续时间互不相等的若干活动组成的维修任务，维修时间服从对数正态分布，如一些机电、电子、机械设备等；对于经短时间调整或迅速换件即可修复的功能单元，维修时间服从指数分布。

2.2.1 维修时间服从正态分布时的贝叶斯更新

可修单元维修时间服从正态分布时，可记作t～N(μ,σ2). 维修时间概率密度函数为

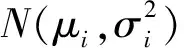
可设定二维随机变量(μ,σ)服从先验均匀分布，其先验概率密度函数为

(8)

根据现有维修时间序列t1,t2,…,tn，利用(5)式可得联合概率密度：

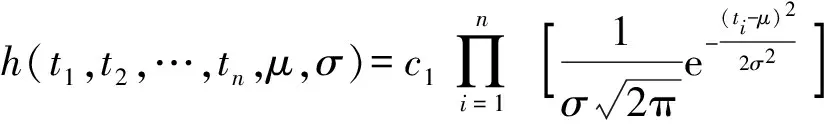
(9)

进而利用(6)式得(μ,σ)的后验概率密度函数：

π(μ,σ|t1,t2,…,tn)=

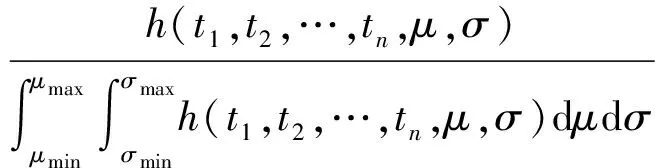
(10)

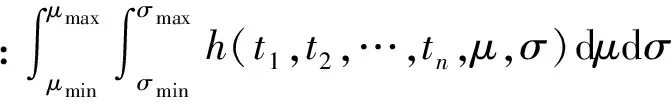
分别计算随机变量(μ,σ)关于μ和σ的后验边缘概率密度函数π(μ|t1,t2,…,tn)、π(σ|t1,t2,…,tn)：

π(μ|t1,t2,…,tn)=

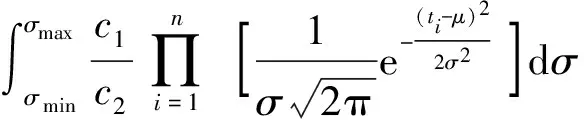
(11)

π(σ|t1,t2,…,tn)=

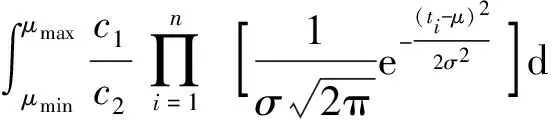
(12)

从而利用(7)式计算μ和σ的后验期望估计值为

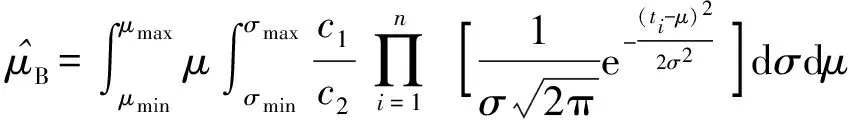
(13)

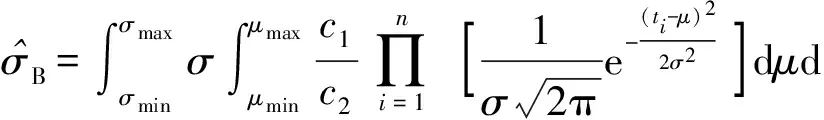
(14)

2.2.2 维修时间服从对数正态分布时的贝叶斯更新

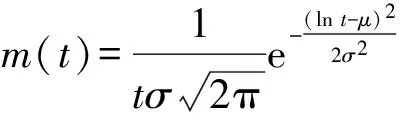
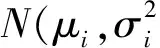
根据现有维修时间序列t1,t2,…,tn，利用(5)式可得联合概率密度：

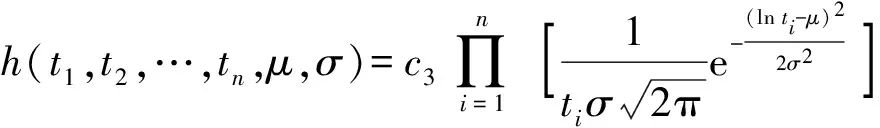
(15)

进而利用(6)式得(μ,σ)的后验概率密度函数：

π(μ,σ|t1,t2,…,tn)=

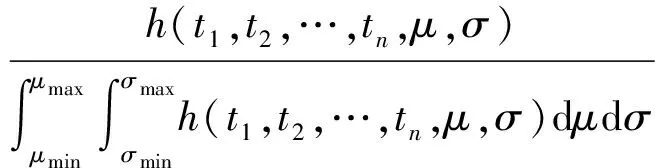
(16)

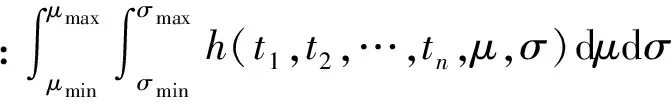
继而利用(1)式中步骤计算得

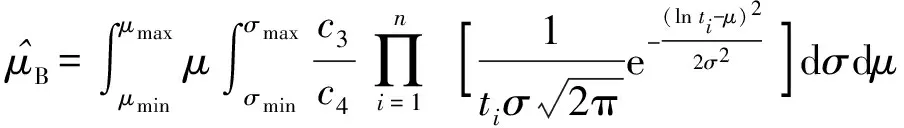
(17)

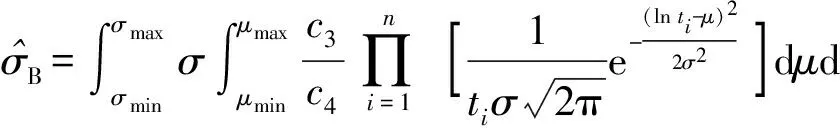
(18)

2.2.3 维修时间服从指数分布时的贝叶斯更新

可修单元维修时间服从指数分布时，可记作t～Exp(λ). 维修时间概率密度函数为m(t)=λe-λt.

首先，根据同类功能单元维修数据确定维修时间的最小值与最大值(tmin与tmax)。令λmin=1/tmax，λmax=1/tmin，可设参数λ的先验分布为区间[λmin,λmax]上的均匀分布，先验概率密度函数π(λ)=1/(λmax-λmin)。

根据现有维修时间序列t1,t2,…,tn，利用(5)式可得联合概率密度：

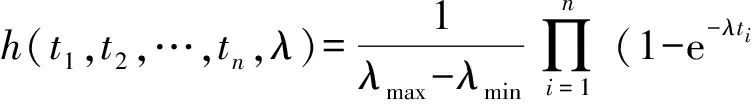
(19)

进而，可利用(6)式计算参数λ的后验概率密度函数：

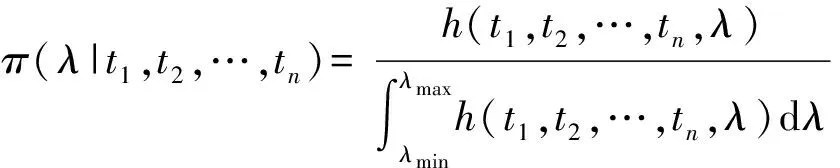
(20)

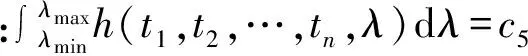
利用(7)式计算参数λ后验期望估计值：

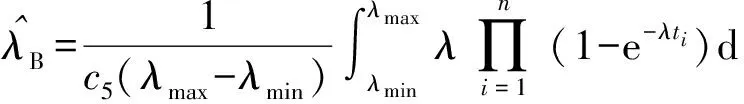
(21)

3 可修单元组合故障事件排除概率计算方法

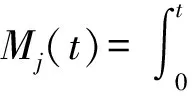
然而，多个函数卷积的解析式通常较难获取，以至于很难计算概率分布函数Mj(t). 实际上，在确定的时间t下Mj(t)是可估计的。因此，可通过曲线拟合的方式获取时间t与Mj(t)之间的近视函数关系。基于这一思路，本文给出Mj(t)计算步骤如下：

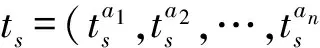
2)重复步骤1共r次，得r组数据ts，其中数值r根据所需计算精度选取，r越大精度越高；

3)分析障事件Ej中发生故障的可修单元，从每组数据中抽取相应数据，得r组针对Ej中可修单元的维修时间数据；

4)根据装备所有可能执行任务类型的允许维修时间集合，确定出装备执行某任务时允许维修时间的可能取值区间[Tmin,Tmax]，在该区间内等间隔选取m个时间参数T1,T2,…,Tm，以参数Tk为例，将步骤3中获取的r组数据分别求和，统计求和结果不大于Tk的组数，并计算该数目与整体数据数量的比值qk(可近似为Mj(Tk))，同理共构建m个二维向量：(T1,q1),(T2,q2),…,(Tm,qm)；

5)将步骤4中获取的m个二维向量进行拟合，获取以时间变量T为自变量，比值q为应变量的函数表达式。将函数表达式中T用t代替，q用Mj(t)代替，可得Mj(t)解析式。

利用上述步骤，可获取各故障事件的排除概率分布函数，进而计算给定维修时间T内的各故障事件排除概率M(E1),M(E2),…,M(E2n-1). 根据各可修单元故障概率p(a1),p(a2),…,p(an)，利用(2)式计算各故障事件发生概率P(E1),P(E2),…,P(E2n-1). 最终利用(4)式计算得可修单元组合E的任务维修度M(E).

需要指明的是，本文在计算可修单元组合任务维修度时假设各功能单元故障发生概率为确定值。此时，利用文中方法可获得较为精确的计算结果。至于各功能单元故障发生概率的精度问题，鉴于篇幅有限，此处暂不予考虑。

4 示例分析

设某装备在任务过程中可修单元共有3个，记作A、B、C，其中：A维修时间服从正态分布；B维修时间服从指数分布；C维修时间服从对数正态分布。已知3个单元在任务过程中发生故障的概率分别为p(A)=0.2，p(B)=0.15，p(C)=0.2. 现对3个单元组成的可修单元组合E={A，B，C}的任务维修度进行评估。

4.1 可修单元维修时间概率密度函数估计

以可修单元A为例，统计该单元维修时间(min)数据为{32.5，39.6，17.1，34.2，31.3，22.3，27.1，31.4，49.2，44.7，22.1，46.2，33.5，29.2，33.4，28.4，28.8，37.7，37.2，37.3}。

统计与可修单元A类似单元的维修数据。

经验数据1(min)：

{37.6，24.8，25.3，26.9，13.5，41.1，34.0，27.2，40.6，21.2，31.4，30.5，34.0，34.0，26.6，31.8，31.0，36.0，38.9，39.0}。

经验数据2(min)：

{22.9，31.2，35.1，39.1，42.4，31.6，20.0，25.5，23.1，48.4，26.4，36.5，29.6，37.6，25.3，20.6，20.5，34.6，29.7，29.5}。

经验数据3(min)：

{24.2，31.6，35.3，46.3，27.1，32.1，30.5，19.6，28.4，20.4，36.0，25.8，31.6，27.8，32.8，27.5，33.9，35.4，41.1，29.9}。

将上述4组数据代入(8)式～(14)式计算，可得可修单元A维修时间(min)服从均值为30.9，标准差5.5的正态分布。同理，利用贝叶斯更新方法可求得可修单元B维修时间(min)服从均值为45的指数分布；可修单元C维修时间(min)服从均值为4.8，标准差为0.1的对数正态分布。分别采用传统估计方法和贝叶斯更新方法得到的A、B、C的维修时间概率密度函数曲线如图1所示。

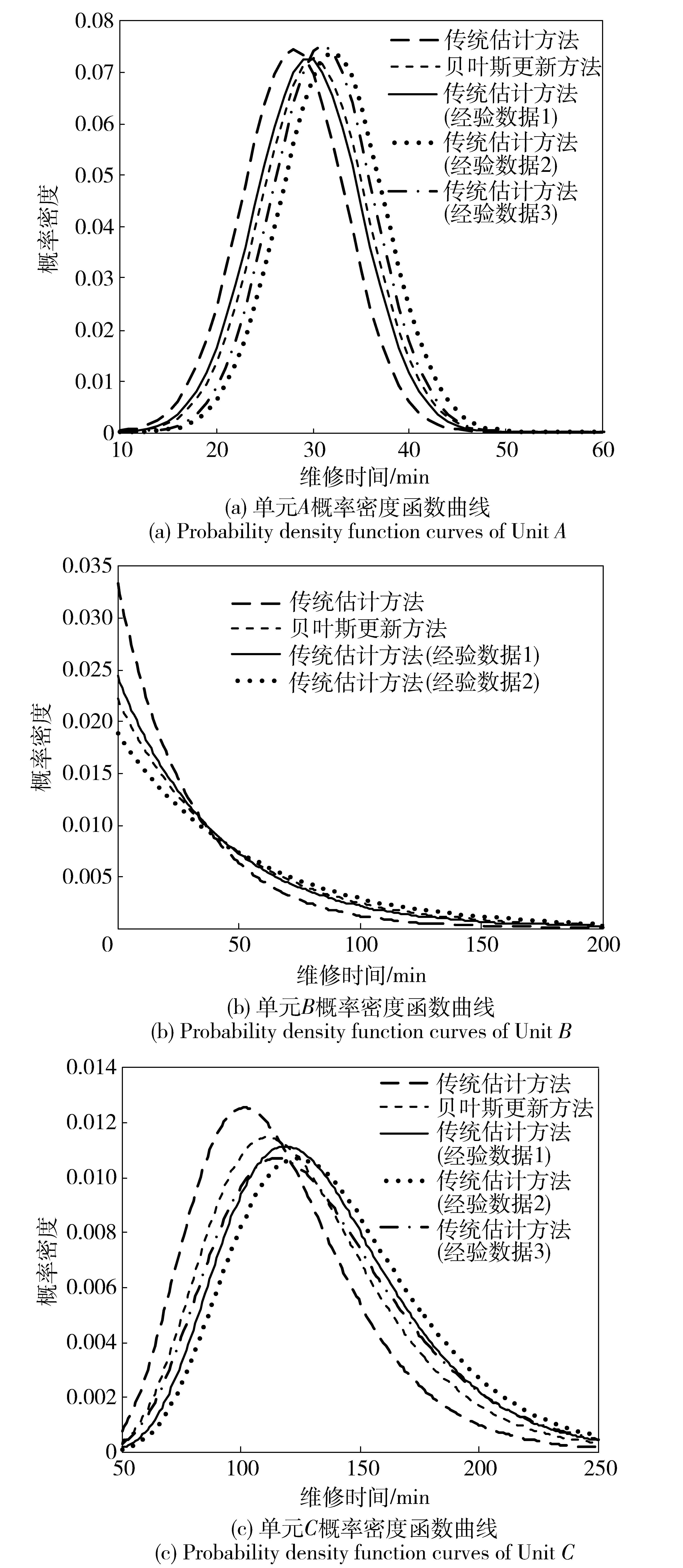
图1 维修时间概率密度函数曲线图Fig.1 Curves of maintenance time probability density function

分析图1中3个单元维修时间概率密度函数曲线特征可知，采用传统估计方法时，维修时间概率密度函数仅与现有数据相关；采用贝叶斯更新方法时，维修时间概率密度函数与现有数据与经验数据均相关。当现有数据可有效反映实际分布特征时(见图1(a))，采用传统估计方法与贝叶斯更新方法所得密度函数相近；当现有数据不能反映实际分布特征时(见图1(b)和图1(c))，采用贝叶斯更新方法所得密度函数可更好地反映真实分布。

4.2 可修单元组合故障事件排除概率分布函数估计

假定，根据经验判断该可修单元组合在任务过程中允许的最大维修时间T通常在120～240 min之间。

分析可修单元组合E所有可能故障事件，可知共有7类故障事件。

故障事件E1：可修单元A发生故障，可修单元B、C不发生故障。此时，故障事件发生概率P(E1)=0.136；故障事件被排除的概率分布函数M1(t)为满足均值为30.9、方差为5.5的正态分布概率分布函数。

故障事件E2：可修单元B发生故障，可修单元A、C不发生故障。此时，故障事件发生概率P(E2)=0.098；故障事件被排除的概率分布函数M2(t)为满足参数为0.022的指数分布概率分布函数。

故障事件E3：可修单元C发生故障，可修单元A、B不发生故障。此时，故障事件发生概率P(E3)=0.136；故障事件被排除的概率分布函数M3(t)为满足对数均值为4.8，对数方差为0.1的对数正态分布概率分布函数。

故障事件E4：可修单元C不发生故障，可修单元A、B发生故障。此时，故障事件发生概率P(E4)=0.024；故障事件被排除的概率分布函数记作M4(t)。

故障事件E5：可修单元B不发生故障，可修单元A、C发生故障。此时，故障事件发生概率P(E5)=0.038；故障事件被排除的概率分布函数记作M5(t)。

故障事件E6：可修单元A不发生故障，可修单元B、C发生故障。此时，故障事件发生概率P(E6)=0.024；故障事件被排除的概率分布函数记作M6(t)。

故障事件E7：可修单元A、B、C均发生故障。此时，故障事件发生概率P(E7)=0.006；故障事件被排除的概率分布函数记作M7(t)。

现对M4(t)、M5(t)、M6(t)、M7(t)进行估计。令n=106，m=41，利用第3节中提出的仿真步骤进行仿真，得4个函数曲线如图2所示。

图2 故障排除概率分布曲线图Fig.2 Probability distribution curves of troubleshooting

对函数曲线进行拟合，其中M4(t)、M5(t)采用高斯函数拟合精度最高；M6(t)、M7(t)采用傅里叶函数拟合精度最高。最终得

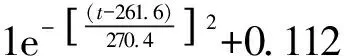
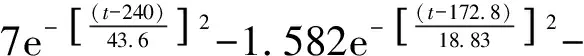
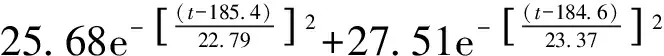
M6(t)=0.492 7+0.371cos(0.024 6t)-

0.321 6sin(0.024 6t)+0.036 21cos(0.049 2t)+

0.090 01sin(0.049 2t),

M7(t)=-43.99-32.72cos(0.011 19t)+

60.44sin(0.011 19t)+16.78cos(0.022 38t)+

25.14sin(0.022 38t)+5.965cos(0.033 57t)-

0.353 1sin(0.033 57t).

4.3 计算可修单元组合任务维修度

令任务中允许的最大维修时间为130 min，可知各故障事件被排除的概率为M(E1)=1，M(E2)=0.944 4，M(E3)=0.750 3，M(E4)=0.888 2，M(E5)=0.040 2；M(E6)=0.186 5，M(E7)=0.004 4.

将已获取的各故障事件发生概率及被排除的概率代入(4)式，可计算可修单元组合E的任务维修度M(E)=0.774 8.

5 结论

本文针对现有方法无法评估多个功能单元组合任务维修度这一问题，提出了一种可修单元组合任务维修度评估方法，对可修单元组合任务维修度进行了评估。

着重对评估过程中的两个关键内容展开讨论。针对传统方法不能准确估计少数据或不完全统计数据情形下的维修时间概率密度函数问题，提出了基于贝叶斯更新理论的功能单元维修时间概率密度函数估计方法；针对多个函数卷积难以计算的问题，提出了可修单元组合故障事件排除概率计算方法。

文中方法弥补了传统任务维修性评估方法中的不足，能够有效评估给定任务剖面内的装备可修单元组合任务维修度。

References)

[1] GJB451A—2005 可靠性维修性保障性术语[S]. 北京:中国人民解放军总装备部, 2005. GJB451A—2005 Reliability, maintainability and supportability terms[S].Beijing: General Armament Department of PLA, 2005. (in Chinese)

[2] Qiang M, Liu L, Yuan F, et al. Complex system maintainability verification with limited samples[J]. Microelectronics Reliability, 2011, 51(2):294-299.

[3] Gao X L, Barabady J, Markeset T. An approach for prediction of petroleum production facility performance considering Arctic influence factors[J]. Reliability Engineering and System Safety, 2010, 95(8):837-846.

[4] Barabadi A, Barabady J, Markeset T. Maintainability analysis considering time-dependent and time-independent covariates[J]. Reliability Engineering and System Safety, 2011, 96(1):210-217.

[5] 朱伟亭. 反水雷装备系统维修性建模分析探讨[J]. 舰船科学技术, 2012, 34(9):134-137. ZHU Wei-ting. The maintainability modeling of MCM weapons equipment system analysis to explore[J]. Ship Science and Technology, 2012, 34(9):134-137. (in Chinese)

[6] 封会娟, 刘祥凯, 唐彦峰, 等. 基于Matlab的导弹营基本任务维修性仿真[J]. 战术导弹技术, 2012(4):48-52. FENG Hui-juan, LIU Xiang-kai, TANG Yan-feng, et al. Simulation on basic mission maintainability of missile-battalion based on Matlab[J]. Tactical Missile Technology, 2012 (4): 48-52. (in Chinese)

[7] 毕军, 王少萍, 石健. 面向任务的单武器系统平均修复时间模型[J]. 北京航空航天大学学报, 2007, 33(3):354-356. BI Jun, WANG Shao-ping, SHI Jian. Mean time to repair modeling oriented unit-mission for weapon system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(3):354-356. (in Chinese)

[8] 封会娟, 于永利, 张柳, 等. 机动防空任务聚合级装备作战单元维修性仿真[J]. 计算机技术与发展, 2009, 19(11):230-233. FENG Hui-juan, YU Yong-li, ZHANG Liu, et al. Simulation model of aggregated equipment combat units' mission maintainability based on mobile aerial defense mission[J]. Computer Technology and Development, 2009, 19(11):230-233. (in Chinese)

[9] 周栋, 吕川, 王美慧, 等. 基于时间特性的系统维修性分配改进方法[J]. 北京航空航天大学学报, 2010, 36(6):713-718. ZHOU Dong, LYU Chuan, WANG Mei-hui, et al. System maintainability allocation improved method based on the time character[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(6):713-718. (in Chinese)

[10] 陆中, 孙有朝, 吴海桥. 基于着色随机时间Petri网的维修性建模方法[J]. 机械工程学报, 2011, 47(10):185-191. LU Zhong, SUN You-zhao, WU Hai-qiao. System maintainability modeling method based on colored stochastic time Petri net[J]. Journal of Mechanical Engineering, 2011, 47(10):185-191. (in Chinese)

[11] 路红山, 许建, 张京伟, 等. 潜艇动力系统任务维修性建模[J]. 中国舰船研究, 2008, 3(4):10-14. LU Hong-shan, XU Jian, ZHANG Jing-wei, et al. Modeling of maintainability based on mission of submarine power system[J]. Chinese Journal of Ship Research, 2008, 3(4):10-14. (in Chinese)

[12] Lira V, Tavares E, Maciel P. An automated approach to dependability evaluation of virtual networks[J]. Computer Networks, 2015, 88:89-102.

[13] 沈军, 张耀辉. 基于状态预测与评估的部件任务成功性评估研究[J]. 系统工程理论与实践, 2013, 33(10):2695-2700. SHEN Jun, ZHANG Yao-hui. Evaluation of dependability of unit based on state evaluation and prediction[J]. Systems Engineering-Theory & Practice, 2013, 33(10): 2695-2700. (in Chinese)

[14] Zhu B J, Frangopol D M. Reliability assessment of ship structures using Bayesian updating[J]. Engineering Structures, 2013, 56(6): 1836-1847.

[15] Behmanesh I, Moaveni B, Lombaert G, et al. Hierarchical Bayesian model updating for structural identification[J]. Mechanical Systems and Signal Processing, 2015, 64/65: 360-376.

[16] 茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程[M]. 北京:高等教育出版社, 2004. MAO Shi-song, CHENG Yi-ming, PU Xiao-long. The tutorial of probability theory and mathematical statistics[M]. Beijing:Higher Education Press, 2004. (in Chinese)

Research on the Evaluation of Mission Maintainability of Repairable Unit Constitution

HAN Xiao-hai1， ZHANG Yao-hui1， WANG Shao-hua1， CAO Xing-wei2

(1.Department of Technology Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 2.The Third Engineer Scientific Research Institute, General Staff Department, Luoyang 471023, Henan, China)

The traditional mission maintainability evaluation method cannot effectively estimate the overall maintenance time of equipment in specific task profile. An evaluation method which can be used to evaluate the mission maintainability of repairable unit constitution is proposed. During evaluation, the maintenance time probability density function of functional unit is estimated using a Bayesian updating approach, and the maintainability of failure event of repairable unit constitution is calculated in a simulation way. The example analysis shows that the proposed method may not only solve the estimated inaccuracy of maintenance time probability density function of functional unit due to incomplete statistical data, but also calculate the convolution of multiple functions conveniently. The assessed result of mission maintainability is more credible.

ordnance science and technology; repairable unit constitution; mission maintainability; Bayesian updating; failure event

2016-01-06

武器装备预先研究项目(2011JJ1105)

韩小孩(1987—)，男，博士研究生。E-mail:hanleiacd@163.com； 张耀辉(1960—)，男，教授，博士生导师。E-mail:zyh532@sohu.com

TJ81+0.7; O212.8

A

1000-1093(2016)11-2058-08

10.3969/j.issn.1000-1093.2016.11.014