数形巧结合，构建实效数学课堂

姚君礼

【摘要】小学阶段是学生学习数学知识的启蒙时期，在这一阶段渗透数形结合的思想，可使数学教学达到事半功倍的效果。要求教师要从数学发展的全局着眼，从具体的教学过程着手，有目的、有计划地进行渗透数形结合思想方法的教学，使学生逐步形成数形结合思想，并使之成为学习数学，解决数学问题的工具，这是我们数学教学着力追求的目标。

【关键词】小学数学 数形结合 有效引导 提高效益

【中图分类号】G4 【文献标识码】A 【文章编号】2095-3089（2016）22-0270-02

数形结合是数学解题中常用的思想方法，使用了数形结合的方法，很多问题便迎刃而解，且解法简捷。在新课程理念下，教学中我注重运用“数形结合”的思想方法，借助数与形的相互转化来促进学生对知识的理解和掌握，培养学生解决问题的能力，使学生的数学思维能力得到了提升，提高了课堂实效。

一、数形结合思想在概念学习中的促进作用

概念学习对三年级学生来说，不仅深奥，枯燥，更是抽象的。因为概念一般是直接给出的，是学生以前没有接触的，但这些知识都要学生记忆，理解并会运用。这对学生的抽象思维能力是一个巨大的挑战，也是能力培养的契机。

㈠分数概念教学

《分数的初步认识》是在小学数学范围内，教材安排的从整数到分数是数概念的一次扩展，借助图形，培养学生的几何直观能力，同时也让学生清楚的看到，分数是在平均分的基础上学习的，体现的是部分与整体的关系。

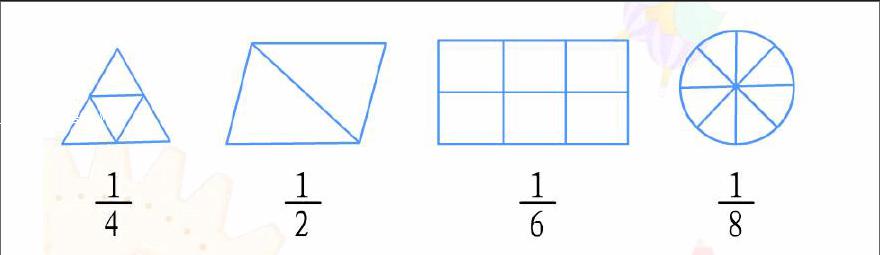
为了突破分数教学的难点，进一步利用数形结合思想，通过以数示形的教学——在图形中表示出分数。

比如：

这里，十分直观形象的考察了学生是否掌握分数的概念，以填图的方式让学生明确，分数的本质就是整体与部分的关系。

因此，在分数概念教学中渗透数形结合思想，图形的直观表现很好的这一知识点的难点，有利于培养学生的几何直观能力和抽象思维能力。更难得的是，学生掌握了以形助数，以数示形两种思维方式，并实现两者的融会贯通。

㈡余数概念教学

学生之前接触到的都是整除的情况，对于有余数的出现，学生显得懵懂茫然，不知所措，所以，这个知识点又是对学生的一次挑战。

由于学生抽象思维能力及其薄弱，因此填鸭式的教学无法帮助学生理解余数，更无法让学生明确余数与除数的关系。这时，利用数形结合思想的指引，引导学生在实际情境中摆，让学生真切的看到最后剩下的物体不能再分，再给出余数的概念，学生能容易接受。同时，学生也在直观的物体中，理解了余数是怎样产生的，进而让他们发现除了之前学的整除，还有余数的除法。通过继续引导，学生还会进一步发现，余数一定比除数小。相信，有了直观的经验，学生在计算中更会注重余数和除数的关系，从而提高学生的计算能力。

当然，如果只是停留再摆的阶段，那么学生的思维能力不会有更大的进步。当学生发现，有的情况摆不了时，他们会发现画图的方法，更简洁，清楚。比如：把红、黄、白三种颜色的花插入花瓶中，红花插5朵，黄花插3朵，白花插2朵，现在红花27朵，黄花19朵，白花10朵，一共可以插多少个花瓶？

学生在已有基础上，对于一种颜色的花朵分配有了数量关系的认知：花朵总数，每份数量，份数。但在这样的实际问题中，让学生直接解答很有难度，即使学生列式解决了，也不一定能真正理解。而这里，采用以形助数的思维方式，可以帮助学生理解，同时在这道题中渗透符号意识，以数形结合思想方法为载体，培养学生的符号意识，有利于学生数学能力的培养。

二、数形结合思想对学生数量分析能力提高的促进作用

数量关系的分析一般是学生解决实际问题的前提，而三年级学生数学成绩容易下滑的一个重要原因就是学生在解决实际问题部分失分过多。因此，提升学生的数量分析能力有利于提高学生的数学思维能力，培养学生爱数学的兴趣。

㈠分数比大小

比大小是最常见的数量关系，也是数量关系建立的基础。三年级上册将比大小由整数扩展到了分数。在整数范围内，学生已经熟练了以形助数的思维方式比大小，所以在分数比大小的内容里，学生又可以延续这种思维方式。

比如：

学生借助图形理解数量大小，将复杂的问题简单化，直观化，这是一种解决问题的策略，提高学生的数学学习能力。

㈡倍数关系

一、二年级的教材中，对于多多少和少多少的问题，学生会借助线段图来帮助自己理解题意。对于倍数关系，学生在二年级“倍的认识”中有所了解，但并没有涉及到应用。

但三年级上册安排了：路程问题，工作总量问题以及价格问题。三年级学生的生活经验不够丰富，如何帮助学生寻找到这些问题的内在联系，是提升学生数学学习能力的一个关键。

借助学生已有的知识经验，利用画线段图，达到简化数学语言的目的，同时也有利于学生排除多余信息，明确题中的数量关系。利用数形结合思想，学生将倍数问题化难为易，化抽象为直观，对于学生解决实际问题的能力提升有着显著的帮助。

三、数形结合思想学生思维能力培养的促进作用

㈠培养学生有序，有条理、全面的思考问题

无论是在学习还是生活中，培养学生有序、全面思考是促进学生思维发展的体现。《数学广角》作为新增单元，对学生的思维能力提出了更高要求。如何将生活中的原形问题数学化，这是对学生的挑战。通过分析，学生运用符号化的思想，将搭配问题在纸上一一呈现，在这个过程中，学生就要考虑搭配什么，怎么表示，搭配的先后顺序，如何表示搭配，怎样搭配有序，全面，而不遗漏。正是这个数形结合的过程，培养学生有序，有条理、全面的思考问题，体现了学生思维能力的提升。

⑵培养学生简洁直观地表达思考的过程与结果

对于简单的排列组合，学生可能通过枚举法能一一呈现出来，可当组合对象越来越多时，如何简洁而直观的反应出学生的思维过程和最后的结果？

数学提倡简洁、明了。因此利用数形结合思想，将搭配问题用画图连线的方式表达，借助符号简化实物，将复杂的问题简单化，抽象问题直观化，进而达到利用计算的方式思考。 这个过程不仅提高了学生的几何直观能力，同时也增强了学生的符号意识。让学生在后续的学习中有更好的发展。

教学的过程如同一个人的成长过程，总是在不断地探索和发现，当然也缺不了别人的帮助。教师作为教学的有心人，只有深入研究教材，将数形结合思想方法的教学发展成为一种有意识的教学活动，才能帮助学生走出思维的误区，引领学生爱学习、乐学习。