简议数学发现中的再发现

江苏省江阴市华士高级中学(214421)

费振东●



简议数学发现中的再发现

江苏省江阴市华士高级中学(214421)

费振东●

科学中的每个新发现.即使它的实际应用暂时还无法实现.但都会给发现者本人和他人带来衷心的喜悦.数学中的众多发现正是因此而作为一门重要学科其千姿百态的各种发现激励和鼓舞着无数的人们.“在伟大的发现或伟大的理论中，那种稳定的联系或更高的统一是通过相似模式的阶段而达成的.”同时也证实了：“许多科学发现就是从以前认为不相同或没有联系的事件之间找到一个共同的特征或联系.”这也使我们懂得了数学中的许多发现实际上都是一种再发现.

共同特征；统一；再发现

尽管数学里的发现方法多种多样，但我认为众多发现实际是一种再发现.也可以说，许多发现就是从以前认为不相同或没有联系的事情之间找到的共同特征或联系.我们看下面的实例：

勾股定理，托勒密定理，欧拉定理，这三大定理在几何学中都是我们熟知的：

①勾股定理：直角三角形两直角边的平方和等于斜边的平方.②托勒密定理：圆内接四边形两对角线的积等于两组对边乘积之和.③欧拉定理：在线段AB上任取两点C，D，则AC·BD=AD·BC+CD·BA.

这三个定理的发现似乎是一个谜，关于①的发现我们可能见到过一个古老的传说故事.勾股定理又叫毕氏定理，据考证，人类对这条定理的认识，少说也超过 4000年其中有文字记载的最早的证明是毕达哥拉斯给出的.据说当他证明了勾股定理以后，欣喜若狂，杀牛百头，以示庆贺.故西方亦称勾股定理为“百牛定理”.遗憾的是，毕达哥拉斯的证明方法早已失传，我们无从知道他的证法.又据记载，现时世上一共有超过300个对这定理的证明.可是，对于②和③是怎么发现的呢？几乎无法得知.我们看这三个定理分别发现的时间表：

定理名称勾股定理托勒密定理欧拉定理发现时间公元前700-600年公元前330年-275年公元前1707-1783年

如果关于勾股定理发现的传说故事是真实的话，那么定理②，定理③是如何发现的呢？由于过去人们注重的是发现的结论，因此各种资料书刊很少记载发现的过程.加之一般的发现者不愿透露自己的发现的秘密，所以对此无法考证.但我在研究考查“托勒密定理”的发现时，偶然发现了后两个定理②和③发现的秘密：①特殊; ②一般;③极端.

粗看三大定理毫无联系，但从统一的角度把三者联系起来，就发现三者之间有深刻的联系.还可以看出后者的发现实质上前者发现中的再发现.由此也可猜想出②和③的发现过程.

我们用数学语言表达就是：在直角三角形△ABC中，a2+b2=c2.

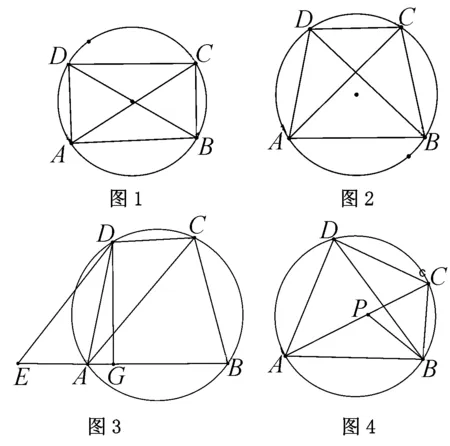
如果将a2+b2=c2写成aa+bb=cc，就可以看成是矩形的两组对边之积.由于矩形的四个顶点是共圆的，我们把矩形放入圆中考虑，就成为圆内接矩形的两组对边乘积之和等于两对角线的积(图1)

如果我们把矩形改变为梯形，边与对角线还是否有上面的关系呢？等于即AB·DC+AD·BC是否等于AC·BD.因为圆内接梯形定为等腰梯形，所以AD=BC,AC=BD，上面式子就成为 AB·DC+AD2是否等于AC2(图2)

如图3，平移CA到DE，过D作DG⊥AB于G，则可证得AB·DC+AD2=AC2.

利用勾股定理，四边形ABCD为等腰梯形，DE∥AC，

∴AE+2AG=AB,∴AG2=AB·DC+AD2AE2+2AG·AE=AB·AE,DG2+(AG+AE)2=AD2+AB·DC,DE2=AB·DC+AD2.∴AC2=AB·DC+AD2.

因此，四边形为梯形时，“两组对边乘积之和等于两对角线的积”是正确的.

若把梯形改成其他四边形进行探索，最后变为一般的圆内接四边形，看上面类似的结论还是否成立，即AB·DC+AD·BC是否等于AC·BD.

证明：作∠PBA=∠DBC(图4).

∵∠PBA=∠DBC,∴△PBA∽△DBC,

∴AB·CD=AP·BD(1).

∴△CPB∽△DAB,∴BC·AD=CP·BD(2).

(1)+(2)得AB·DC+AD·BC=AC·BD.

这一等式的成立就正是托勒密定理.

从文中所经历的时间表中，可以看出：仅就这样一点认识上的飞跃——新发现②.经历了大约四百年，这就说明了人们要打破常规来认识一个已经熟悉的问题并非易事.虽然托勒密在当时打破了毕达哥拉斯(或商高)的认识①，但他没能进一步深思下去.两千年后，欧拉又把托勒密的认识推向了极端.他假设圆的半径无限增大，而圆周上的四点 就落在同一直线上，从而发现了③.(证明略)

从上述过程看出，三大定理的统一恰好说明了：“在伟大的发现或伟大的理论中，那种稳定的联系或更高的统一是通过相似模式的阶段而达成的.”同时也证实了：“许多科学发现就是从以前认为不相同或没有联系的事件之间找到一个共同的特征或联系.”这也使我们懂得了数学中的许多发现实际上都是一种再发现.

[1]数学发现的艺术[M].青岛海洋大学出版社

[2]初等数学研究课程[M].湖南教育出版社

[3]初等代数研究[M].高等教育出版社

G

B