一元函数极限计算方法综述

长春建筑学院基础教学部(130607)

付美鑫●



一元函数极限计算方法综述

长春建筑学院基础教学部(130607)

付美鑫●

在实际生活中,对实际问题的研究,往往是通过函数来实现的,但对于很多求精确解的问题,仅仅通过有限次的算术运算是不能得到的,这就需要考察对于自变量的一个无限变化的过程,函数值具有怎样的一个变化趋势,也就产生了极限的思想,本文主要介绍极限的运算方法.

定义 设函数f(x)在点x0的某个去心邻域内有定义,如果当x趋于x0(或)时,对应的函数值f(x)无限的接近于某个确定的常数A,就说A是函数f(x)当x→x0(或x→)时的极限,记作或f(x)→A(x→x0()).

现对极限的运算方法做如下总结:

一、直接代点法

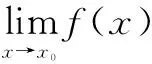
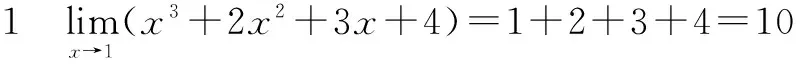
二、有理分式

p(x)=a0xn+a1xn-1+…+an-1x+an,

Q(x)=b0xm+b1xm-1+…+bm-1x+bm,

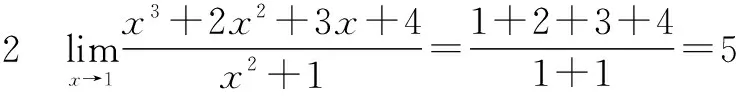
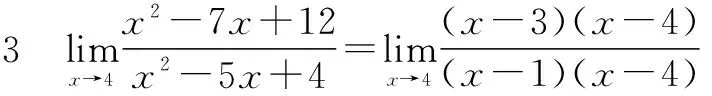
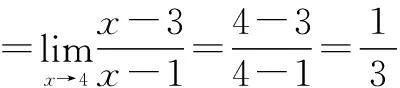
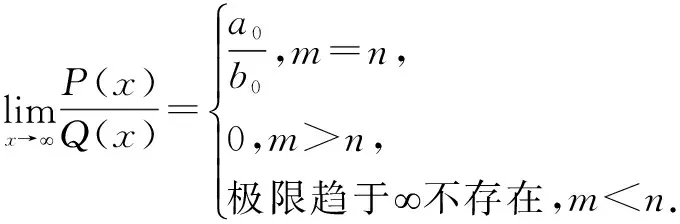
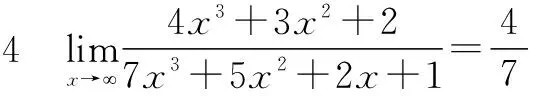
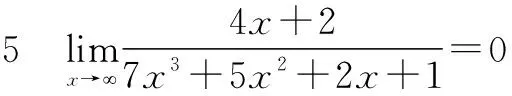
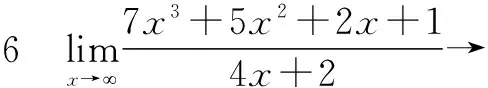
三、分子(分母)有理化法

当分子或分母有根式时,优先考虑分子(分母)有理化法.

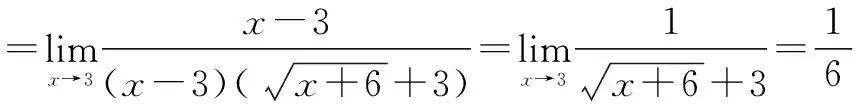
四、利用等价无穷小计算极限

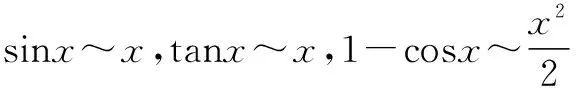
arcsinx～x,arctanx～x,ln(1+x)～x,ex-1～x.

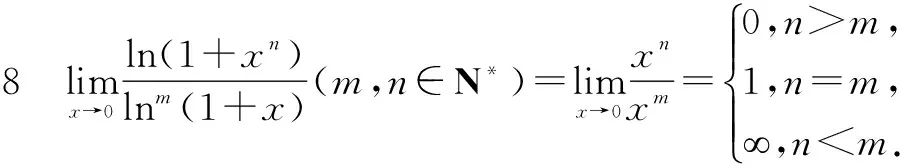
五、夹逼准则

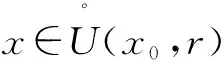
在应用夹逼准则计算极限时,要对函数f(x)做适当的放大和缩小.

六、利用重要极限计算极限

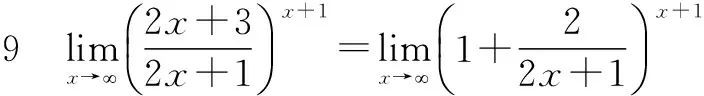
=e=e.

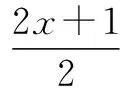
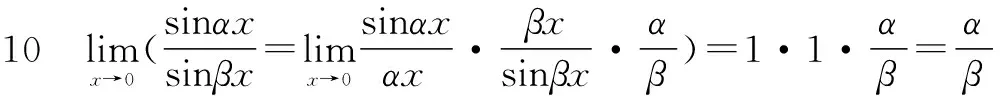
G632

B

1008-0333(2016)33-0002-01