阀控式铅酸电池老化实验及其失效性预测方案

张文圳，杨睿哲，张延华

(北京工业大学电子与控制工程学院，北京100022)

阀控式铅酸电池老化实验及其失效性预测方案

张文圳，杨睿哲，张延华

(北京工业大学电子与控制工程学院，北京100022)

为了实现对阀控式铅酸蓄电池失效性的有效检测，建立了以内阻变化率为依据的预测模型。根据电池老化实验，所测得的电池内阻，电压，充放电流，温度等数据进行回归分析。通过回归分析得到蓄电池内阻随放电时间的关系，推导出内阻的变化率函数。同时根据大量的实验数据分析、估计出当蓄电池内阻增加到其基准值的30%，放电容量达到80%时的斜率值范围，并根据内阻变化率来建立预测模型。实验结果表明：阀控式铅酸蓄电池内阻随着时间变化趋势接近三次函数和指数函数，以内阻变化率来建立模型预测蓄电池失效时期比内阻更加可靠和精确。

阀控式铅酸蓄电池；回归分析；内阻变化；失效预测

蓄电池作为电力系统的后备电源，确保其性能的稳定是非常重要的，蓄电池使用一段时间后，经常发生容量下降的现象，严重时导致蓄电池失效，使用寿命提前终结[1]。另外蓄电池组是由一定数量的单体电池串联组成的，某个单体蓄电池故障就会导致整个蓄电池组故障或损坏[2-4]，而当发生故障，仍需要持续供电时，该电池无法提供电量，会扩大事故。因此用可行的预测方案对蓄电池失效前期做预测有重大的意义[5-6]。

目前，对于阀控式铅酸蓄电池的时效性研究，已有实验和方案表明，蓄电池失效的主要标志体现在电容量的降低和内阻的增大。然而蓄电池本身的容量和内阻很难准确测量，而且不同型号测量仪器所测的内阻有很大的误差，所以通过内阻增大到其基准值的30%的点作为更换电池的时间也会有很大的误差[7]。

本文通过对老化电池进行大电流反复充放电，加速电池的老化速度，进而拟合出电池的内阻随时间的变化趋势，并对当电池内阻值增大到30%时，电阻的变化率做出统计分析，并把该统计平均值作为替换蓄电池的基准。根据电池老化实验数据拟合出的内阻随时间的变化趋势，推导出其斜率的变化趋势，再根据斜率的变化趋势建立预测模型。

根据电池内阻变化率来预测阀控式铅酸蓄电池的失效时期，可以有效地避免由于测量仪器所带来的误差。因此以内阻变化率函数建立预测模型能够更好地预测电池的性能。

1　VRLA工作原理

铅酸蓄电池的正常充放电的化学方程式为：

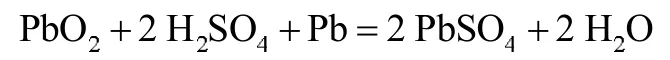
在放电时，正极由二氧化铅(PbO2)变成硫酸铅(2PbSO4)，发生还原反应，将化学能转换成电能向负载供电。铅酸蓄电池放电反应原理如图1所示，反应方程式为：

铅酸蓄电池放电的总反应式为：

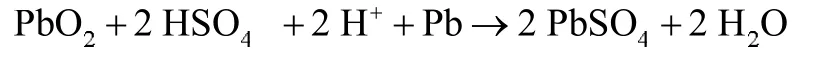
图1　蓄电池放电反应原理

由以上化学方程式可以得出，铅酸蓄电池在使用过程中，电池会失水，导致电解液比重增高、引起电池正极板的腐蚀，使电池的活性物质减少，从而使电池的容量降低而失效。铅酸蓄电池在充放电过程中，当电荷不足时，正负极板上PbSO4会长期存在，进而失去活性，不能够再参加到化学反应中，使电池的活性物质减少，降低了电池的有效容量。蓄电池在恒压充电时，充电电流和电池温度累计，使蓄电池的工作温度过高，造成蓄电池的损坏。

2　VRLA的老化实验及数据分析

通过对单体阀控式蓄电池反复进行大电流放电，加速电池的老化，记录放电过程中内阻、电压、时间等参数，对所测多组数据进行分析，并对内阻值与放电时长及放电容量做数据拟合，最终根据对多次所得数据的分析，并用线性函数、对数函数、指数函数、多项式函数四种函数做回归分析合。

测试电池：

A组：光宇公司2 V/200 Ah，型号为GFMD-200；

B组：华达公司2 V/500 Ah;

C组：光宇公司2 V/300 Ah，型号为GFMD-300;

D组：光宇公司2 V/1 000 Ah，型号为GFMD-1000。

电池状态：A，B，C，D四组阀控式铅酸蓄电池是均已使用多年的旧电池，平均寿命为5～7年;测量仪器为Hioki 3551单电池内阻测试仪。

2.1电池的老化实验

实验方法：初期对A组01号电池进行25 A/8 h恒流放电，并进行20 A/5 h恒流充电；后期进行100 A/1 h恒流放电，30 A/3 h恒流充电。在充放电过程中使用单电池内阻测试仪测量电池的充/放电电压、充/放电电流、内阻和电池体温度，放电过程结束后计算放电容量。

对A组其余电池，B组，C组电池也进行100 A/h的恒流放电，30 A/3 h恒流充电。在充放电过程中使用单电池内阻测试仪测量电池的充/放电电压、充/放电电流、内阻和电池体温度，放电过程结束后计算放电容量。

2.2数据分析与结果

分别对A组01号电池的多次大电流放电，A组其余电池，B组，C组电池大电流放电时所测内阻和记录时间所组成的离散的点分别进行线性函数、对数函数、指数函数、多项式函数拟合。

通过数据的回归分析得出结果是：阀控式铅酸蓄电池线性函数，对数函数拟合结果差，指数函数和多项式函数拟合得非常好。

因此可以总结出，对于阀控式铅酸蓄电池这类电池，其内阻随时间的变化趋势非常接近三次函数或指数函数。它们的拟合优度都在0.96以上。

(1)指数函数式回归分析

图2是单体蓄电池第30次放电所得的内阻与放电时间的数据。通过回归分析可知，拟合优度R2=0.961 42，说明蓄电池内阻和放电时长的关系非常接近指数函数曲线，显著性系数Sig值小于0.05，说明该回归关系具有统计学意义。

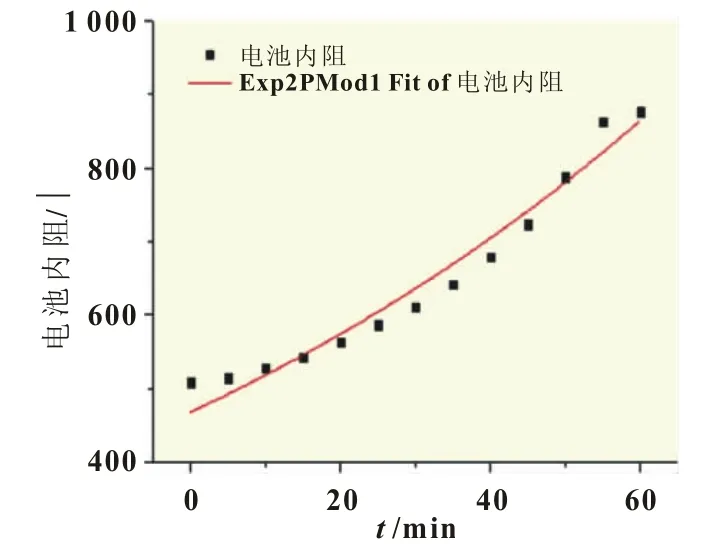
图2　单体蓄电池第30次放电的内阻与放电时间数据的指数函数回归分析

(2)三次函数式回归分析

图3是单体蓄电池第30次放电所得的内阻与放电时间的数据。通过回归分析可知，拟合优度R2=0.993，说明蓄电池内阻和放电时长的关系也非常接近三次函数曲线，显著性系数Sig值小于0.05，说明该回归关系具有统计学意义。

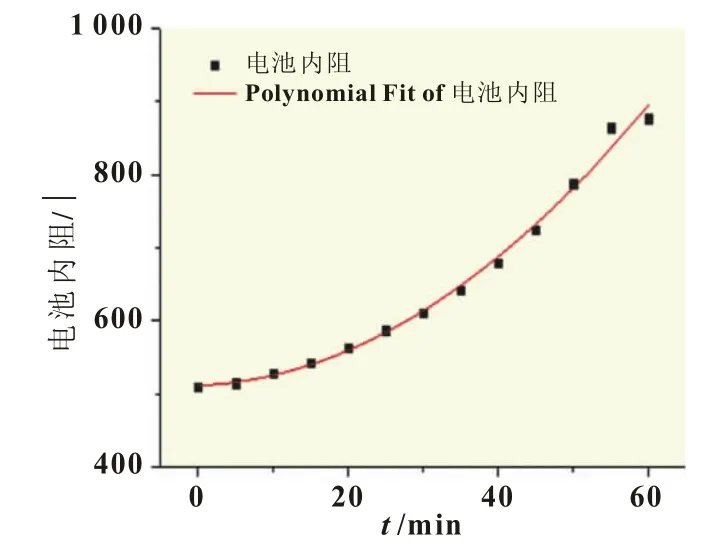
图3　单体蓄电池第30次放电所得内阻与放电时间数据的三次函数回归分析

通过对比上述两种曲线的拟合优度可知，三次函数曲线比指数函数曲线更接近测量值。

3　建立预测模型

3.1建模依据

美国BTECH公司2004年发布的电池测试指南(The Complete Guide To Battery Monitoring V2.0，BTECH Inc，www. btechinc.com)中指出：

(1)在达到80%容量点之后的电池能量是很难精确预测的，确定从80%点到电池的彻底劣化的时间，就像在图4中所显示的t时间段一样，那是不确定的。

(2)由于VRLA电池的特性已经通过BTECH所显示的那样是无法预测的，估计剩余容量或者剩余时间从根本上就是不精确的。BTECH认为提供一个精确剩余时间在技术上是不可能的。

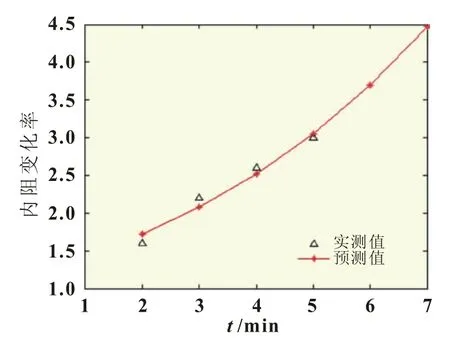
图4　GM(1,1)预测模型预测的结果

(3)当蓄电池内阻增长到基准内阻的30%与80%的电容量交点，是推荐立即更换电池的时间点，也是确定电池服务时间的时间点。

(4)唯一的方式来确保VRLA电池系统的完整性是通过在内阻增长30%时替代电池组中的劣化电池，达到30%内阻值的时间点由BTECH检测系统告知用户。

所以,根据以上几个结论，我们希望能够通过计算统计当内阻增长到基准值的30%时的斜率值，来预测更换电池的时间。

通过对A组所测蓄电池的内阻达到其基准内阻值的20%～30%之间的内阻斜率做了一个统计，所得的结果为1.24～1.27。

3.2建模

根据老化实验所得的拟合曲线可推知，阀控式铅酸蓄电池的内阻变化率趋势可采用指数型公式 (1)和多项式型公式(2)：

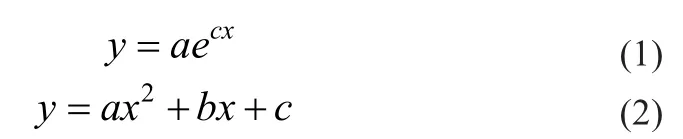
分别针对公式(1)和(2)建立数学模型：对于公式(1)建立GM(1,1)模型[8-9]，对于公式(2)建立二次函数：y=dx2+ex+f模型来预测阀控式铅酸蓄电池的内阻的变化率，进而推断出电池的更换时间。

GM(1,1)灰色预测模型是一种指数增长模型,当参数呈指数规律持续变化时,用此方法进行预测,可获得较高的预测精度。因此,用GM(1,1)灰色预测模型对蓄电池的性能状况进行预测评估实用性很好。另外,灰色模型还具有所需样本数据少、计算简便、可检验等优点。

用MATLAB建立GM(1,1)模型和二次函数y=dx2+ex+f模型。将一组等时距t检测到的斜率值代入到GM(1,1)模型即可检测到下次的斜率值，或代入到模型y=dx2+ex+f中，模型利用这些数据算得相应的系数a，b，c的值，然后可预测出下个t时刻的斜率值，或者想要得到的某一时刻t'时的斜率值。

仿真实例，用这两个模型分别对第25次所测得的斜率值进行预测；测得的前六次的斜率为[1.2 1.6 2.2 2.6 3.0 3.5]；输入前五次的值，用 GM(1，1)模型预测结果为：[1.200 0 1.721 0 2.083 4 2.522 0 3.053 0 3.695 8]，第六次的结果为：3.695 8，图4是用MATLAB软件建立的GM(1,1)模型的预测值和实测值的曲线。而用二次函数模型测得的结果为：[1.171 4 1.674 3 2.148 6 2.594 3 3.011 4 3.400 0],第六次的结果为3.400 0，实际测量的值是3.500 0。图5是用MATLAB软件建立的二次函数模型的预测值和实测值曲线，由此可得二次函数测得的结果更接近于真实值。

图5　二次函数预测模型预测结果

4　小结

电力系统对直流电源的可靠性要求极高，因此准确地预测电池失效性的时间是非常有意义的。根据斜率来检测蓄电池的性能并预测阀控式铅酸蓄电池的服务和更换时间，比内阻来预测蓄电池的失效时间更加准确。同时通过这种预测模型也能预知蓄电池的潜伏性故障及其发展趋势,从而提前对蓄电池运行状况做出诊断,及时对将要失效的电池进行技术检查,再根据预测结果决定是否更换电池,防止因失效电池而引起的事故。

[1]黄素斌,胡恒生.航空化学电源原理和使用维护[M].济南:黄河出版社,1998.

[2]SVOBODA V,DOERING H,GAREHE J.The influence of fast charging on the performance of VRLA batteries[J].Journal of Power Sources,2005,144:244-254.

[3]郭屹松，李铁香.基于CAN总线的蓄电池智能监测系统[J].计算机测量与控制，2006,14(5):1-5.

[4]王红旗，李辉，陶慧.基于CAN现场总线的智能温度采集模块的设计与实现[J].计算机测量与控制，2006，14(1)：125-127.

[5]章异辉.基于现有监控系统的蓄电池精确监控与故障预测方法[J].通信电源技术,2008,25(2):84.

[6]黄海宏,王海欣,庄翔,等.电动汽车分布式电池充放电管理的研究[J].电子测量与仪器学报,2009,23(6):68-69.

[7]BTECH.The Complete Guide To Battery Monitoring V2.0[EB/OL]. [2015-10-23].www.btechinc.com.

[8]王丰效.GM(1,1)组合预测模型及其应用[J].统计与决策,2006 (11):142-143.

[9]段锋,杨芬.灰色预测模型的研究及应用[J].湘南学院学报,2008, 29(2):17-20.

VRLA batteries experimental study of aging and failure prediction scheme

ZHANG Wen-zhen,YANG Rui-zhe,ZHANG Yan-hua
(College of Electronics and Control Engineering,Beijing University of Technology,Beijing 100022,China)

In order to realize the effective detection of failures of VRLA batteries,a prediction model based on impendence variance rate was established.In the battery aging test,the measured impendence,voltage,charge and discharge current and temperature of the battery were used for regression analysis.The relationship between internal impendence and discharge time was obtained by regression analysis,and the impendence variance rate function was derived.According to the large amount of experiment data,the range of slope values was valued when the simultaneous analysis of the estimated battery internal impendence increased to 30%of its reference value,and the discharge capacity reaches 80%.And then,according to the variance rate of impendence,the predictive model was built.The experimental results show that:VRLAB impendence variance trends over time,is very close to a cubic function and exponential functions.The prediction model based on impendence variance rate is more reliable and accurate than the internal impendence.

VRLA;regression analysis;impendence variance rate;failure prediction

TM 912.1

A

1002-087 X(2016)10-2014-03

2016-03-17

张文圳(1989—)，男，甘肃省人，硕士研究生，主要研究方向为蓄电池检测技术。