自适应小波算法在配电网电流保护中的应用研究

冯 斌 李开鑫 马 涛 赵 启 朱建华

（国网新疆电力公司电力科学研究院，乌鲁木齐 830011）

自适应小波算法在配电网电流保护中的应用研究

冯 斌 李开鑫 马 涛 赵 启 朱建华

（国网新疆电力公司电力科学研究院，乌鲁木齐 830011）

Morlet复小波算法在计算电力系统基波分量时比传统的傅里叶算法有更高的精确度，为了更好的发挥该算法的优越性，本文主要分析了Morlet复小波算法自身参数变化时对计算基波分量精度的影响，并在此基础上提出了一种具有自适应性的Morlet复小波算法，最后仿真结果表明所提出的具有自适应性的Morlet复小波算法在配电网电流保护中的应用是可行的。

自适应电流保护；Morlet复小波；自适应Morlet复小波算法；配电网

目前，配电网主要继电保护方式仍然为传统的电流保护，且需要人工整定。在配网大规模发展以后，保护整定工作量将大幅增加。自适应电流保护能根据运行方式的变化、故障类型的不同等因素实时生成或调整保护动作门槛，从而使保护动作性能始终保持在最佳状态，并且无需人工整定计算。

自适应电流保护的关键技术是，实时监测系统运行状态和快速判定故障类型。实时监测系统运行状态和快速判定故障类型都需要精确提取稳态相量的幅值，现有保护装置多依靠傅里叶算法进行计算，当配网出现直流分量、各次谐波分量或频率抖动时，傅里叶算法误差较大。文献[1]在计算工频向量幅值时只将 Morlet复小波算法与傅里叶算法进行了对比，并进行了仿真验证，但是未对Morlet复小波算法本身参数在变化时对计算精度的影响进行探讨。为此本文将对此方面的问题进行进一步讨论，并提出了具有自适应性的Morlet复小波算法，通过该算法对自适应电流保护中最核心的系统阻抗计算部分进行仿真验证，结果证明此算法具有更高的计算精度。

1 自适应电流保护及Morlet复小波算法

1.1 自适应电流保护原理

自适应电流速断保护能根据当前电力系统实际运行方式和故障状态实时、在线确定故障发生时的故障类型系数和系统电源侧实际阻抗，计算出电流整定值，其整定公式[2]为

式中，Krel为可靠系数，一般取1.2～1.3；Kf为故障类型系数；由故障类型识别结果决定。三相短路时，取Kf=1；两相短路时，取；E为系统的等效相电势；Zc为系统电源侧的综合阻抗（即电力系统实际运行方式）；Zl为被保护线路的阻抗。

该式与传统速断保护整定公式的区别除了多出一个故障类型系数 Kf之外，还在于电源侧阻抗 Zc与系统等效电源的相电势E都不再是常数，这些参数都需要根据实测的电流电压数据计算得到。

1.2 Morlet复小波算法

傅里叶算法采用的是矩形窗函数，若选择Gauss函数作为窗函数，则Morlet复小波算法，其形式[3]为

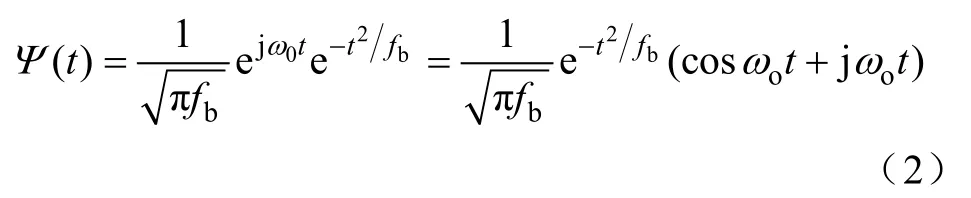
式中，ωo=2πfc；fc为中心频率；fb为带宽；ω≥5，以近似满足容许性条件。

Morlet复小波采用的是时频窗面积最小的高斯窗，时频域局部化性好，而且对称性好，并且为复值小波，其变换结果可同时反应信号的幅值和相位关系，其离散表达式为

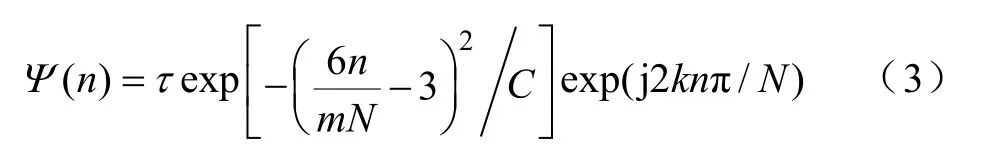
式中，τ 为满足归一化条件的比例系数，即

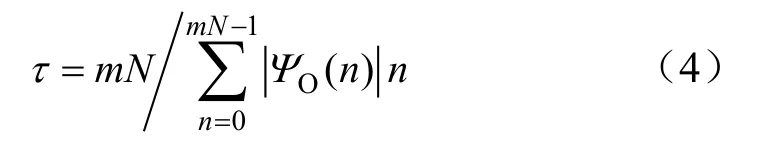
式中，m为时间窗大小；N为一周采样点数；c为频宽调节系数；k为谐波次数；n为小波函数的离散点数。

对于任意一信号f(n) 的离散小波变换为

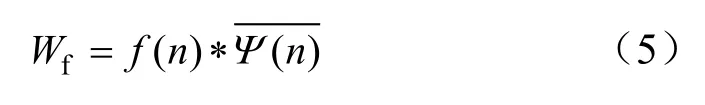
式中，“∗”表示卷积。

1.3 Morlet复小波算法自身参数对信号提取的影响

因为配电网具有结构复杂、谐波分量较大、频率波动大、线路负荷轻重差别较大等特点，故假设配电网发生短路故障或正常运行时的电信号如式（6）所示：

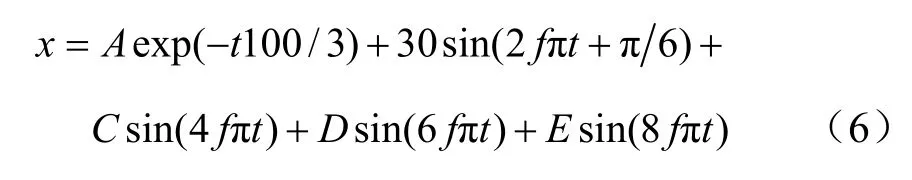
式中，A、C、D、E分别为直流和各次谐波幅值；f为频率。

为确保在复杂环境下保护装置正确动作，现从频率、谐波和信号不断变化的情况出发，分析采样时间窗、采样频率、频宽调节分别对基波幅值计算的影响。

1）时间窗m对信号提取的影响

当N=24、c=2时，通过计算可以得到表1中的测试数据，可以看出：当故障信息中仅含有直流分量时，在m=8时得到精度较高的基波分量；在故障状态仅存在频率抖动时，可以在m=3和4之间得到精度较高的基波分量；在故障状态分别含有二、三和四次谐波时，基本上在m=5时可以得到精度较高的基波分量；在故障状态同时含有直流分量和各次谐波、甚至频率抖动时，可以在m=3和4之间得到较高精度的基波分量。

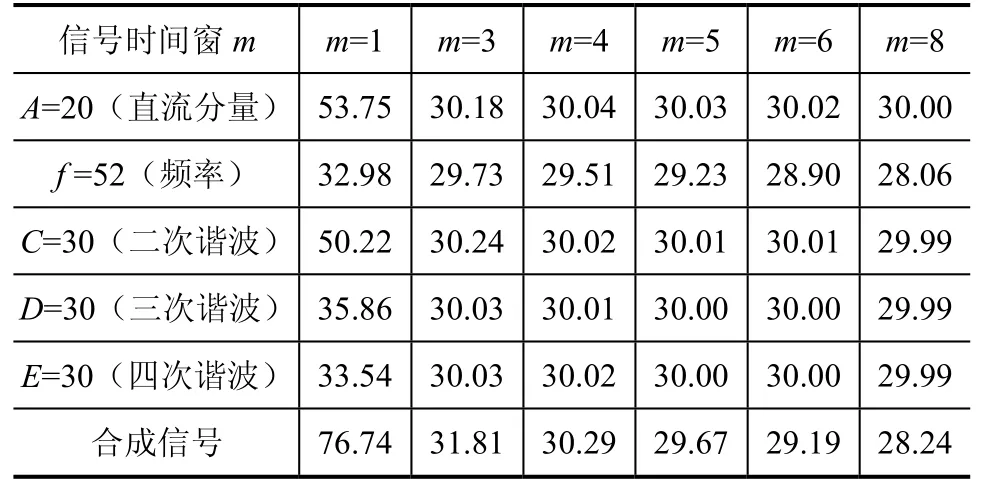
表1 时间窗m对信号提取精度影响的计算结果

2）信号采样频率对信号提取的影响

当m=4、c=2时，通过计算得到表2中的测试数据，可以看出：当故障信号中仅含有直流分量和谐波分量、N=24时，计算精度较高；当频率抖动比较严重、N=24时，计算精度较高。

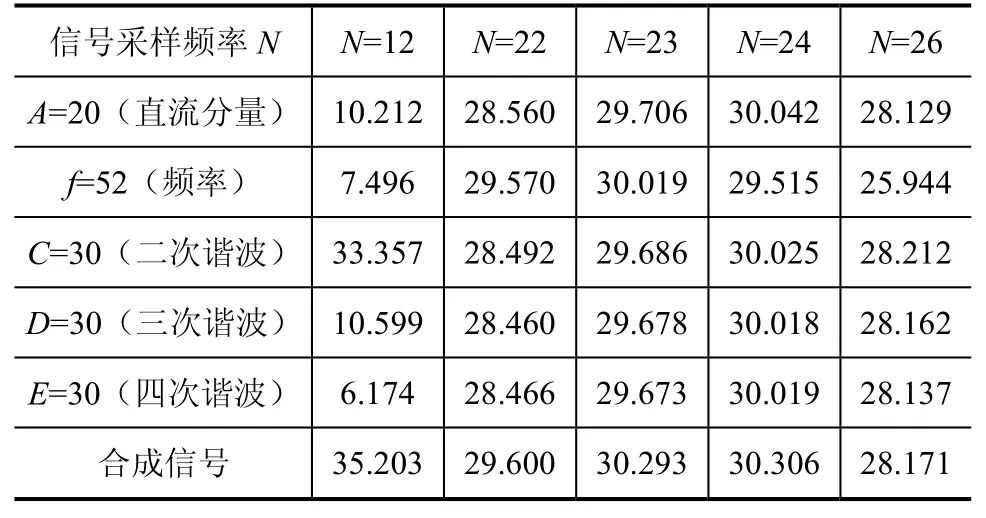
表2 信号采样频率对信号提取的影响计算结果

3）频宽调节系数对信号提取的影响

当N=24、m=4时，通过计算得到表2中的测试数据，可以看出：当故障信号中只含有直流分量和二次以上谐波分量、c=1.5时有较高精度；当频率发生较大抖动、c=0.3时计算精度较高。

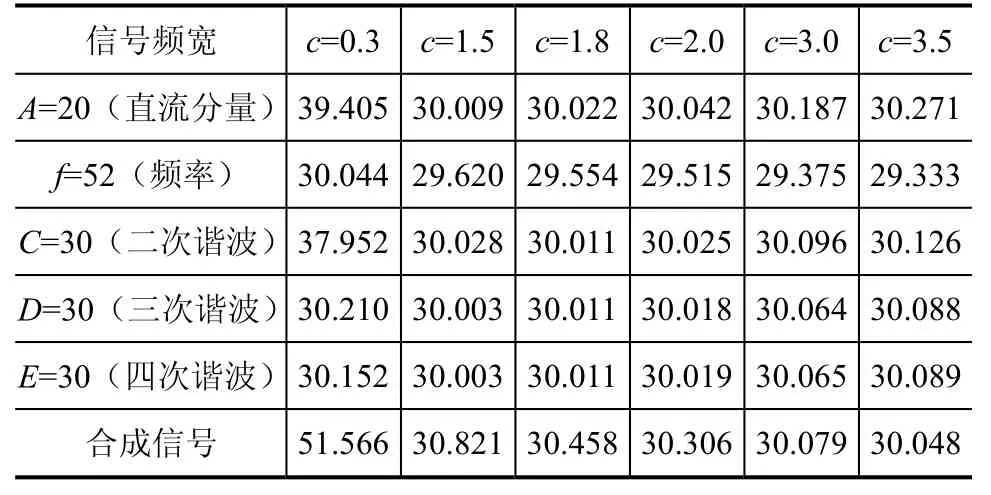
表3 频宽调节系数对信号提取的影响计算结果

1.4 自适应Morlet复小波算法

通过对Morlet复小波算法自身参数对基波分量计算算结果影响分析可知，该算法本身也具有一定的适应性，为此可以设计如图1所示的具有自适应性的Morlet复小波算法。根据各个参数的不同影响，可以设计以下3种自适应性小波算法。

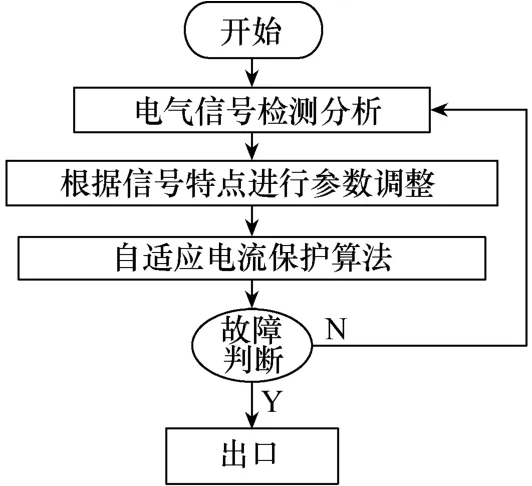
图1 基于自适应小波的电流保护逻辑图

1）时间窗可调的 Morlet复小波算法。该方案总体思路是，首先检测分析故障分量的各种组份，然后根据故障信息特点实时调整时间窗大小（具体判断标准见1.3中论述），设定时间窗大小（可以参考具体工程要求）。

2）采样频率可调的 Morlet复小波算法。该方案的总体思路与时间窗可调的思路基本一致。通过对采样频率的实时调整，可以让保护装置的采样模块在不影响计算精度的情况下更好的发挥作用，以缩短装置判断分析时间。

3）频宽可调的 Morlet复小波算法。该方案总体思路与前两种相同，它的特点就是，在频率抖动情况比较严重的情况下，具有更高的运算精度。

总体来说，以上 3种方案各有特点：方案 1）对频率抖动情况比较严重的故障计算精度较差；方案 2）的计算结果比较折中，具有更好的鲁棒性，但 N=24时对频率抖动严重的计算精度也是相对较差；方案3）与方案2）情况基本相同。通过以上分析可以看出，如果参数实时调整合理，那么该算法在对基波分量提取时有很高的精度。

2 模拟仿真

在自适应电流保护中，系统阻抗的实时计算是最核心部分，因此本文仅通过Matlab和PSCAD对该部分进行了仿真验证，具体过程如下：

假设短路故障电流信号不仅含有衰减的直流分量，而且电网的频率也发生了波动，为了放大频率波动的影响，f取为52Hz，假设输入信号为

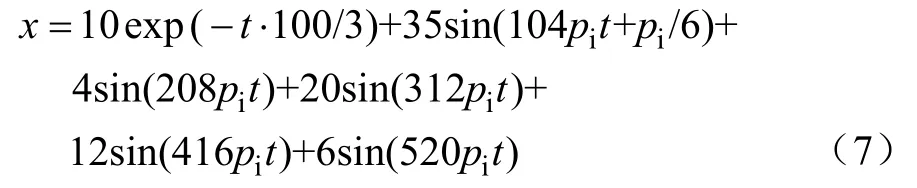
仿真结果如图2所示。由仿真波形图可知，此算法的误差只有 1.82%，能够完全满足电力系统继电保护的要求。

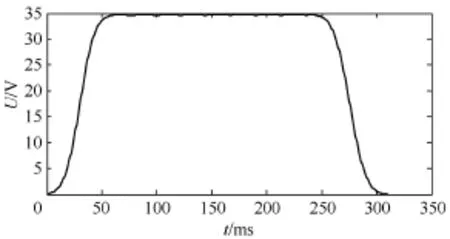
图2 仿真结果

考虑到配电网结构复杂且负荷情况变化快的特点，本文录取了某城市配电网的实时电流曲线（如图3所示），负荷变化大约为20%，并进行了计算，计算结果如图4所示。从图4显示情况可以看出，计算结果满足实际需求。

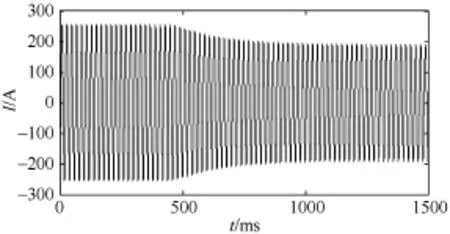
图3 负荷变化曲线

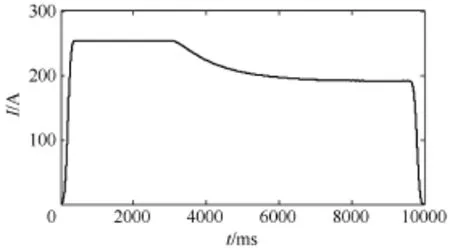
图4 电流幅值计算结果

应用PSCAD搭接如图5所示的配电网模型，进行短路故障模拟，测出短路时保护安装处的故障电压和电流，最后根据自适应电流保护算法算出系统阻抗。由电路图可知，系统阻抗值约为10.44Ω。

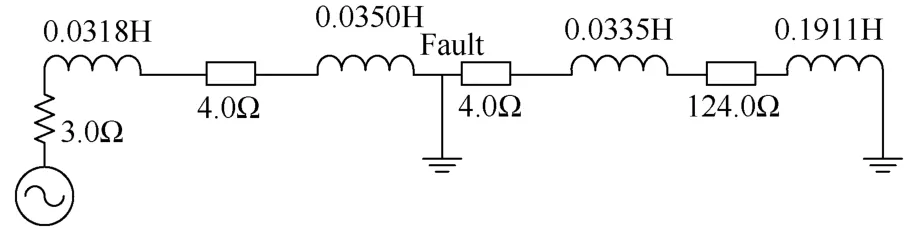
图5 仿真电路模型

通过程序记录保护安装处故障前后的相电压、相电流采样数据，然后根据式（1），利用Matlab计算程序进行仿真计算系统阻抗，计算结果如图6所示。从图中可以看出，此种算法的误差最大只有0.5%左右，要比文献[4]的精度高，从而可以完全保证自适应电流保护的计算精度。

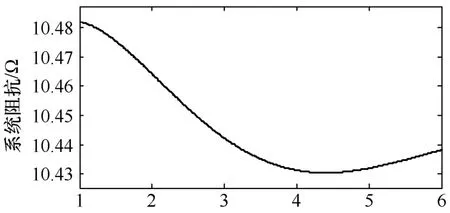
图6 系统阻抗计算结果

3 结论

目前配电网快速发展，分布式电源和电动汽车充电桩将被大量接入配电网中，配电网运行方式将更加复杂灵活，谐波源也将大量融入电网，传统电流保护方式将面临巨大挑战。自适应电流保护技术已被证明是一种有效的解决方案，而自适应电流保护最核心的问题就是系统阻抗的实时计算，系统阻抗精确计算的核心又是基波分量的精确计算，Morlet复小波算法对基波分量精确计算有其显著的优势。为了让Morlet复小波算法充分发挥其优势，本文详细分析了其自身参数对基波分量计算时的各种影响，并在此基础上提出了一种具有自适应性的Morlet复小波算法，最后通过仿真证明了该算法的有效性。基于有适应性的小波算法与自适应电流保护的结合使用，必定能进一步确保配电网的运行安全。目前，该项目仍处于软件分析阶段，关于算法的实际应用效果将在以后的具体工程应用中进行验证。

[1]冯斌.基于小波的自适应电流保护技术的研究[D].西安: 西安工程大学,2012.

[2]张海梁,孙婉胜.自适应电流速断保护在智能配电网中的应用[J].低压电器,2011(20): 5-7,10.

[3]程伟,徐国卿,牟龙华.基于 Morlet复小波的牵引网故障相量估算法研究[J].电工技术学报,2006(2): 108-113.

[4]Feng Bin,Liu Shuguang,Application of MOLET complex wavelet in adptive current protection,proceedings of International Conference on Electrical and Control Engineering (ICECE2011),72-75; EI: 20114614518077.

Application Research on Adaptive Wavelet Algorithm in the Distribution Network Current Protection

Feng Bin Li Kaixin Ma Tao Zhao Qi Zhu Jianhua
(Power Research Institute of State Grid Xinjiang Electric Power Company,Urumqi 830011)

This paper mainly analyzes the accuracy of calculating fundamental component when the Morlet complex wavelet algorithm’s parameter change,and on this basis,this paper proposes a Morlet complex wavelet algorithm with adaptive,finally the simulation results show that with adaptive Morlet complex wavelet algorithm application in power distribution network current protection is feasible.

self-adaptive current protection; morlet complex wavelet; adaptive morlet complex wavelet algorithm; power distribution network

冯 斌（1981-），男，陕西省咸阳市人，硕士，工程师，主要从事电力系统继电保护方面的研究工作。