凹凸率与平均值——琴生不等式的推广：凹凸率不等式

胡卿瑞

（同济大学土木工程2016级 200092）

凹凸率与平均值
——琴生不等式的推广：凹凸率不等式

胡卿瑞

（同济大学土木工程2016级 200092）

根据johan jensen的琴声不等式，从均值与函数及其导数之间的联系中，推导出了与均值有关的不等式及其判定定理，提出一个新的数学概念“凹凸率”，以及与它有关的重要结论“凹凸率定理” 。这个定理揭示了导数、函数与均值的内在联系，给具有均值关系的问题带来很大方便。从本文例题可以看出，这一发现推广了一般均值的定义，这个理论有很大活力，比如：如果一个轮换对称不等式的二元形式成立，则其n元形式必定成立。这是十分有趣而且很有价值的发现，它将给研究轮换对称不等式等问题带来许多便利之处。

均值 凹凸率 函数

一、均值的推广

二、凹凸率与凹凸率函数

1．定义：对定义域内任0x ，可导函数 )(xf 在任意一点处的凹凸率为而为该函数的凹凸率函数。

下面给出证明:

①不妨设x1＜x2，令ϕ 1(x)=g(x)−(k1x+b1)，ϕ2(x)=f (x)−(k2x+b2)，使得

由数学归纳法不难将①②推广至n元的情况，就把①称为凹凸率不等式吧。

3．应用

①用于证明凹凸率不等式

②用于证明均值不等式

当 x＞0时，它们均单调递增，且凹凸率函数满足

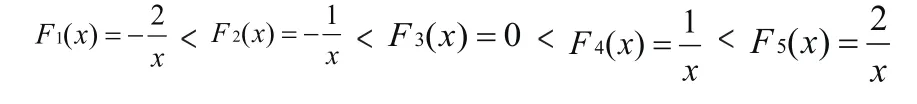
由此可判断

故不等式得证。从上可以看出凹凸率不等式在证明轮换对称不等式中的应用:首先将不等式两端化为均值形式，再找到两端均值对应的函数，再比较原函数凹凸率的大小，最后证明命题。理论上，任何形式的均值均有与其对应的凹凸率函数，但是寻找的方法还需作进一步探究。