脉冲干扰下一类捕食系统的性态分析
程 艳
(山西农业大学信息学院,山西 太谷 030800)
脉冲干扰下一类捕食系统的性态分析
程 艳
(山西农业大学信息学院,山西 太谷 030800)
对一类具脉冲效应的时滞捕食系统进行讨论.首先,对系统中食饵灭绝解的有界性进行分析,进一步利用微分比较定理讨论系统的永久持续生存和灭绝,得到系统的永久持续生存和灭绝的条件.
捕食系统;脉冲;最终有界;局部稳定;持久生存
种群动力学是生物数学的一个重要研究分支.种群动力学的研究主要是基于某一生态系统中各物种进化发展的特性及物种间的生态关系,建立能够反映这一生态系统动力学特性的数学模型,用数学表达式定量地表述种群的发展过程,并通过各种数学理论、数学方法和计算机对这一模型的动力学性态进行定性,定量分析和数值模拟,从而能够揭示和预测种群的发展规律,为保护种群资源和维护生态平衡提供理论指导.考虑到自然界中捕食者种群对食饵种群的捕食功能经常会依赖于二者的比例[1-5],并综合考虑其他各种因素,我们假设捕食者种群密度制约,其增长进程满足Logistic方程,同时对食饵依比率依赖进行捕食,并在固定时刻对其进行脉冲捕获,我们建立了一类更加复杂的带有时滞和脉冲的依比率依赖的捕食系统.系统如下:
(1)
其中x(t),y(t)分别代表食饵和捕食者的密度,r1>0,r2>0表示食饵和捕食者的内秉增长率,a1>0,a2>0分别是它们的种内竞争率,b1>0是捕食者的捕获率,b2>0是食饵食物量转化成新生捕食者的一个度量,m>0是半占领饱和度,是脉冲收获周期.0 令 则系统(1)将转化为: (2) 存在. 考察系统: (3) 我们有如下引理: 引理2设(x(t),y(t),z(t))是系统(2)的解,且其初值满足x(0+)≥0,y(0+)≥0,z(0+)≥0,那么对所有t≥0,均有x(t)≥0,y(t)≥0,z(t)≥0.若x(0+)>0,y(0+)>0,z(0+)>0,则当t>0时,有x(t)>0,y(t)>0,z(t)>0. 证明由系统(2)的前两个方程可得: 则 又由于 故当x(0+)≥0,y(0+)≥0,z(0+)≥0时,恒有 进一步,x(τ+)=x(τ)≥0,y(τ+)=(1-E)y(τ)≥0,z(τ+)=z(τ+)≥0:这样,在区间[τ,2τ]上,同法可证,也有x(t)≥0,y(t)≥0,z(t)≥0.重复上述讨论过程,可得结论成立. 显然,对于系统(2),我们有 定理1 系统的所有具有任意正初值的解是一致最终有上界的. 证明设(x(t),y(t),z(t))是系统具有任意正初值的解. 由于 进而有 (4) 考虑其比较系统: (5) 令y2(t)是系统(2)的任意解.故对任意的ε>0,存在T3>0,当t>T3时,恒有 故当t足够大时,据比较定理有, 取M=max{Mx,My,Mz},定理得证. 注意到 (6) (7) 再由引理1知,当E 故当E 进一步, 我们有 (8) 此处,Φ(t)满足 Φ(0)=1是单位矩阵.系统(2)脉冲条件线性化为 由脉冲方程的Floquet乘子理论,单值矩阵为 由系统(2)有: 考虑相应的比较系统: (9) 根据比较定理知, 对任意的ε>0,存在T4,当t>T4时,有 从而我们有limn→∞x(t)=0成立.进一步可得limn→∞z(t)=0.从而对任意的ε>0,存在T,当t>T时,恒有 考虑其比较系统: 当r1=4,a1=4,b1=2,a2=2.5,m=2.5,r2=3,b2=1.5,E=0.5,τ=1,a=3,x0=10,y0=10,z0=10,r1-b1/m>0且E<1-e-r2τ,满足定理2的条件,则系统(2)是持久生存的.见图1. 当r1=0.5,a1=4,b1=2,a2=2.5,m=2.5,r2=3.b2=1.5,E=0.5,τ=1,a=3,χ0=10,y0=10,z0=10,r1-b1/m<0且E<1-e-r2τ,满足定理3的条件,则系统(2)是灭绝的.见图2. 图1 x(t),y(t),z(t)持久生存的时间序列图 图2 x(t),y(t),z(t)灭绝的时间序列图 [1] Y.Kuang,E.Beretta.Global qualitative analysis of a ratio-dependent predator-prey system[J].Math.Biol,1998(36):389-406 [2] Sanyi Tang,Lansun Chen.Global qualitative analysis for a ratio-dependent predator-prey model with delay[J].Journal Mathematical Analysis Applications,2002(266):401-409 [3] 庞国萍.具有脉冲效应的两食饵-捕食者系统分析[J].数学的实践与认识,2007(16):129-133 [4] Shuwen Zhang,Lansun Chen.Chaos in three species food chain system with impulsive perturbations[J].Solitons and Fractals,2005(24):73-83 [5] Xinzhu Meng,Jianjun Jiao,Lanxun Chen.The dynamics of an age structured predator-preymodel with disturbing pulse and time delays[J].Nonlinear Analysis: Real World Applications,2008,9(2):547-561 [6] Hongjian Guo,Lansun Chen.The effects of impulsive harvest on a predator-prey system withdistributed time delay[J].Commun Nonlinear Sci Numer Simulat,2009(14):2301-2309 Qualitative Analysis for a Predator-Prey System with Impulsive CHENG Yan (College of Information, Shanxi Agricultural University, Taigu 030800,China) A predator-prey system with impulsive was researched. Firstly, to analyze the boundedness of solutions of the prey extinct. Further, by differential comparison theorem, we establish sufficient conditions, which guarantee permanence and extinction for system. predator-prey system; impulsive; boundedness; local stability; permanence 2016-06-08 程 艳(1987-),女,山西晋中人,硕士,山西农业大学信息学院助教,主要从事生物数学研究. 1672-2027(2016)03-0006-06 O175 A1 预备知识



2 持久生存与灭绝

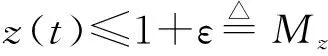


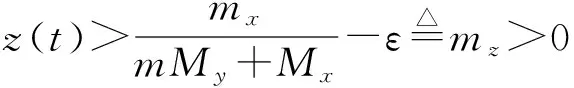


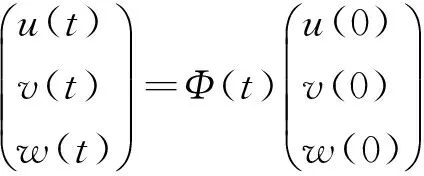



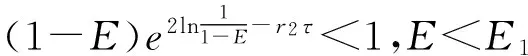

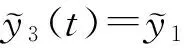



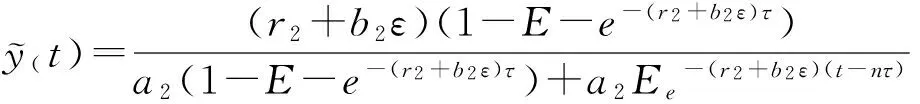

3 小结


4 数值模拟



