基于神经网络的短期电力负荷预测及其MATLAB实现
黄宏运,朱家明,吴礼斌
(安徽财经大学1.金融学院;2.统计与应用数学学院,安徽 蚌埠 233030)
基于神经网络的短期电力负荷预测及其MATLAB实现
黄宏运1,朱家明2,吴礼斌2
(安徽财经大学1.金融学院;2.统计与应用数学学院,安徽 蚌埠 233030)
针对短期电力负荷预测问题,利用MATLAB软件建立日最高温度、日最低温度、日平均温度和平均湿度等气象因素对电力负荷的回归预测模型,具体对比给出BP神经网络与NARX神经网络两种回归预测结果,并通过对隐含层网络参数的调试对BP神经网络进行了适当的改进.
电力负荷预测;气象因素;BP神经网络;NARX神经网络;MATLAB
1 概述
伴随着我国城市化进程与经济水平的不断发展,电力负荷也水涨船高呈现出不断增长的趋势,因而对于电力负荷预测方面的研究也就成了大家关注的热点话题之一.但是一直以来,对于电力负荷的预测也是学术界的难点之一,这主要是由于电力系统的复杂性以及关联电力负荷的影响因素过多造成的,一方面由于历史的电力负荷数据具有规模大、多噪声和非线性等特点,从而要求处理电力负荷预测的系统要具有很好的鲁棒性和非线性拟合能力,另一方面如果只考虑历史数据建立时间序列预测模型明显是不够的,因为电力负荷在很大程度上受到气象因素的影响,所以本文将研究的重点放于气象因素对于电力负荷的回归预测上.
2 数据来源与相关假设
本文的数据来源为第九届“中国电机工程学会杯”全国大学生电工数学建模竞赛A题(本文附件中提供的数据格式为1 106行5列).为了对问题泛化处理,选择2012年1月1日至2014年12月31日(共计1 106 d)A地区日最高温度、日最低温度、平均温度和相对湿度作为输入变量(自变量),对应时间的电力负荷作为输出变量(因变量).为了问题的处理方便我们有以下两点假设:1.由于部分数据缺失(3个数据点),我们对其进行了适当的插值,假设上述处理不会对预测结果产生影响.2.假设数据的来源真实、准确和可靠,即为实际每天的统计负荷数据.
2.1 研究思路
自20世纪以来,神经网络理论已得到不断地发展,作为人工智能核心方法之一的人工神经网络(ANN)已在生物、医药、金融和自动化等领域得到了广泛的运用.基于人工神经网络优良的非线性拟合能力,我们将利用历史原有数据,将气象因素作为输入变量,实际电力负荷作为输出变量,通过训练BP神经网络和NARX神经网络,对比给出两种神经网络的预测结果,以此建立基于神经网络的气象因素对电力负荷的回归预测模型.2.2 研究理论
2.2.1 BP神经网络
BP神经网络是一种多层前馈神经网络,该网络的主要特点是信号向前传递,预测输出与实际输出之间的误差反向传递.在前向传递中,输入变量从输入层经隐含层处理,直至输出层.每一层的神经元状态只影响下一层神经元状态.根据输出层的输出与实际输出之间的误差进行网络权值与阈值的不断调整,直至网络的最终输出无限逼近实际输出.BP神经网络的拓扑结构如图1.
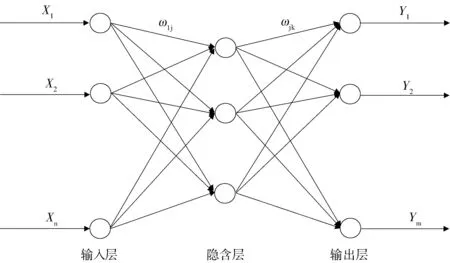
图1 BP神经网络拓扑图
图1中X1,X2,…,Xn为网络的输入值,Y1,Y2,…,Ym为网络的输出值,ωij,ωjk为网络的权值.可以看出,BP神经网络实际上就是完成了从n个自变量到m个因变量的函数映射.
BP神经网络预测前需要训练网络,其主要的步骤如下:
第一步:网络初始化,根据系统输入变量和输出变量的结构确定输入层节点数n,隐含层节点数l,输出层节点数m,初始输入层、隐含层和输出层之间的连接权值为ωij,ωjk,初始化隐含层阈值a,输出层阈值b,给定学习速率和神经元激励函数.
第二步:隐含层输出计算,根据输入变量X,输入层和隐含层间连接权值ωij以技隐含层阈值a,计算隐含层输出H.
上式中,l为隐含层神经元数;f为隐含层激励函数,该函数有多种表达方式,本文所选函数为:
第三步:输出层输出计算,根据隐含层输出H,连接权值ωjk和阈值b,计算BP神经预测输出O.
第四步:计算误差,根据网络预测输出O与实际输出Y,计算网络预测误差e.
第五步:权值与阀值更新,根据网络预测误差e更新网络连接权值ωij、ωjk和阀值a、b.
式中η为学习速率.
第六步:判断算法迭代是否结束,若没有结束,返回第二步,直至算法迭代结束为止.
2.2.2 NARX神经网络
神经网络按照是否存在反馈与记忆可以分为静态神经网络与动态神经网络,NARX神经网络即是一种具有反馈和记忆功能的动态神经网络,它可以将以前时刻的数据保留,使其加入到未来时刻数据的计算,从而使网络不仅具有动态性而且使丢失的系统信息更少.
事实上NARX神经网络是一种带有外部输入的非线性回归神经网络,而NAR神经网络则是一种没有外部输入的神经网络,两者具体的结构对比见图2、图3.

图2 具有外部输入的NARX神经网络
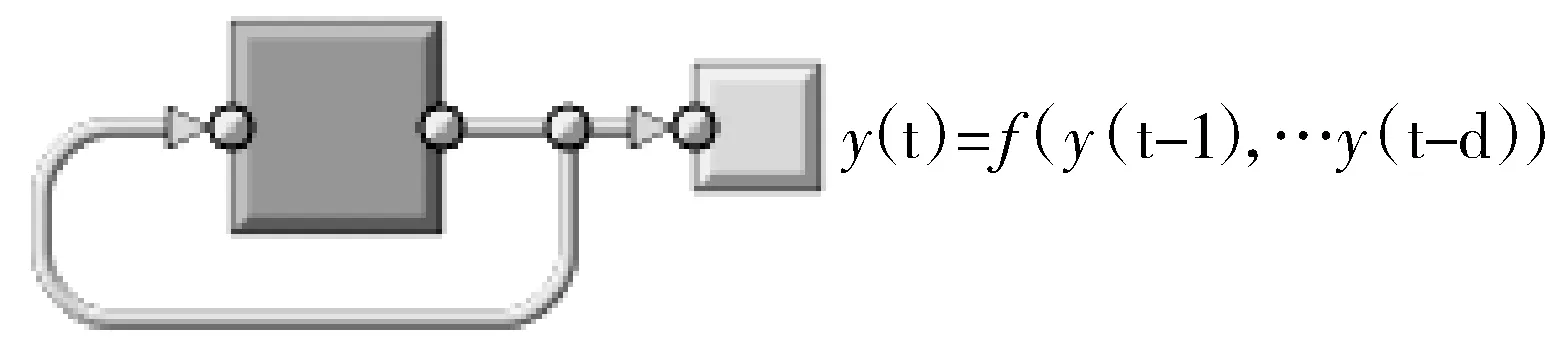
图3 不具有外部输入的NAR神经网络
图2中,x(t)表示神经网络的外部输入;y(t)是神经网络的输出;NARX神经网络的模型可以表示为:

可以看出,NARX神经网络y(t)值得大小取决于上一或多个y(t)和上一或多个x(t),由于NARX神经网络在时序数据预测上保留了较大关联性,所以它被广泛运用于时间序列方面的预测.本文后续正利用NARX神经网络的构造特点,以2011年1月1日至2014年12月31日每一天的气象因素作为输入变量,以对应时期的电力负荷为输出变量,建立电力负荷的时间序列回归预测模型.
2.3 研究过程
2.3.1 BP神经网络预测
首先我们从1106天中选取1000个样本数据作为BP神经网络的训练数据,剩下的106个样本数据作为测试集,为了保证训练集与测试集数据产生的随机性,我们通过产生1000个随机序列数据来进行训练集数据的选取.具体的MATLAB实现步骤如下:
第一步:利用函数mapminmax将选取的训练数据的输入(气象因素)与输出(电力负荷)归一化.
第二步:通过函数newff构建BP神经网络模型,初始的网络参数为:隐含层神经元数为3,最大的迭代次数为1000,学习率为0.1,学习的目标为0.000 04.
第三步:通过函数train对第二步中构建的BP神经网络进行训练.
第四步:利用第三步中训练对的BP网络,通过函数sim对归一化后的测试集输入数据进行仿真,并将预测结果与原始测试集输出数据进行对比.
按照上述步骤,我们得到测试集的平均误差误差大小为154.731 1,平均相对误差大小百分比为5.46%,可以看出,利用BP神经网络建立气象因素的电力负荷回归预测模型的精准度很高,为了使预测输出与实际输出更直观化,我们绘制出BP神经网络输出结果和相对误差大小见图4、图5.

图4 BP预测输出与实际输出 图5 BP网络输出相对误差
为了进一步改进BP神经网络的预测精度,我们对原始的神经网络给予了一定的改进.
改进一:增加隐含层神经元个数,通常来讲,BP神经网络的隐含层神经元个数对BP神经网络的预测精度有较大的影响,尤其是对于复杂的非线性拟合预测.神经元个数太少,网络的训练程度达不到拟合的优度,神经元个数过多,不仅会使时间成本增加,而且容易造成过拟合现象即训练的神经网络对于训练数据的拟合很好,但对于测试数据的拟合误差较大.通常来讲,BP神经网络的预测误差会随着神经元个数的增加呈现先减少后增加的趋势.所以以下我们逐步增加神经元个数以寻找最佳的拟合网络结构,得到的结果如表1和图6所示.

表1 不同隐含层神经元数BP神经网络预测误差
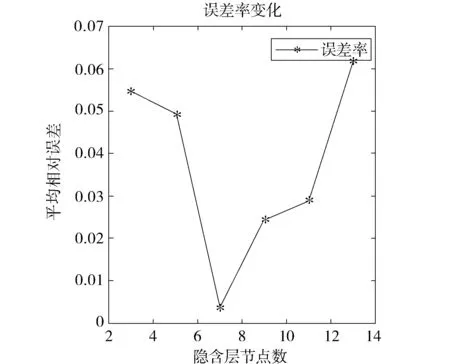
图6 BP神经网络误差率变化
通过表1和图6可以看出,当设置隐含层神经元个数为7个时,平均相对误差最小,预测输出与实际输出之间的拟合程度最高.但是由于受到随机数的影响可能每一次的预测结果都会有一定的误差,但总体不会产生太大的偏差.
改进二:增加隐含层的层数,对于复杂的非线性拟合系统,单隐层神经网络可能无法通过增加隐含层神经元的个数来提高拟合的精度,以下我们改进一的基础之上将原有的单隐层网络结构改为双隐层网络结构,每一层的神经元个数都为7个.
通过表2可知,双隐层神经网络的预测精度较单隐层神经网络的预测精度有所提高,但运行的时间也有所增加.

表2 不同隐含层层数BP神经网络预测误差
2.3.2 NARX神经网络预测
首先我们建立电力负荷的非线性自回归模型,设置输入延时为1∶2(默认值),输出延时也为(默认值),双隐含层(神经元个数均为50),这里的输入与输出延时表示网络的下一个输出与前两个输入、前两个输出存在某种函数映射关系,具体模型表示为:y(t)=f(y(t-1),y(t-2),x(t-1),x(t-2)).
最后我们建立NARX训练网络模型,模型的具体结果如图7.
我们利用建立的NARX神经网络预测模型对测试数据进行预测并给出模型的误差分析图8所示.

图7 NARX神经网络预测模型
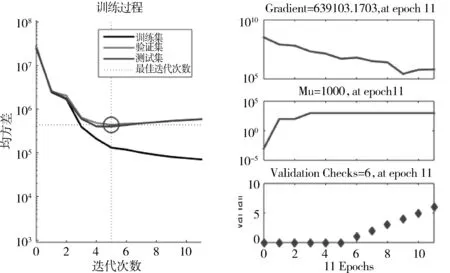
图8 网络训练过程梯度等参数变化
通过图8可以看出,NARX神经网络在训练5次后,验证集的误差上升,说明此时训练可以结束,整个数据此时的误差为218 170.
整个数据集的误差及拟合如图9、图10所示:

图9 预测输出与实际输出间的误差 图10 预测输出与实际输出拟合结果
通过图10可以看出,整体预测数据与实际输出数据的拟合程度在90%以上,说明整体的回归拟合效果较好,但从图九上可以看出还是有许多样本点的预测输出与实际输出存在较大的误差.为了进一步分析误差,我们绘制了误差自相关图和输入与误差相关图.
通过图11和图12我们可以看出,预测输出与实际输出的误差之间存在着严重的自相关,这主要是由时间序列数据的特点导致的,电力负荷数据在时间上存在着滞后效应,即气象因素对电力负荷的影响不仅限于当期,而是延续若干期,由此导致了误差变量严重的自相关.
3 结论
本文上述建立的基于BP神经网络与NARX神经网络电力负荷预测模型对于考虑气象因素的回归预测效果都比较好,但是也存在着严重的不足,具体表现在利用NARX神经网络预测输出与实际输出之间的误差存在严重的自相关.目前对于神经网络算法的优化与改良主要有基于遗传算法的神经网络算法和基于粒子群算法的神经网络算法,可以通过这两种算法对NARX神经网络预测模型给予进一步的改进.

图11 误差自相关图 图12 输入与误差相关图
总的来说,本文给出的两种基于气象因素的短期电力负荷神经网络回归预测模型可以为未来电力负荷的预测提供一定的借鉴,这对机组组合、经济调度、安全校核等都具有一定的现实意义,并且可以将上述的神经网络模型运用于气象预告、水文预告、农作物病虫害预告等各个方面.
[1] 王小川,史 峰,李 洋,等.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社,2013
[2] 陈 明.MATLAB神经网络原理与实例精解[M].北京:清华大学出版社,2013
[3] 任丽娜.基于Elman神经网络的中期电力负荷预测模型研究[D].兰州:兰州理工大学,2007
[4] 飞思科技产品研发中心.神经网络与MATLAB 7实现[M].北京:电子工业出版社,2005
[5] 吕 蝉.基于BP神经网络的短期负荷预测[D].武汉:华中科技大学,2007
[6] 刘 双.基于MATLAB神经网络工具箱的电力负荷组合预测模型[J].电力自动化设备,2003,23(3):59-61
[7] 刘晨晖.电力系统负荷理论与方法[M].哈尔滨:哈尔滨工业大学出版社,1987
[8] 鞠 平,马大强.电力系统负荷建模[M].北京:中国电力出版社,2008
[9] 杨桂元.数学建模[M].上海:上海财经大学出版社,2015
Short-term Power Load Forecasting Based on Neural Network and MATLAB
HUANG Hongyun1, ZHU Jiaming2, WU Libin2
(1.School of Finance, Anhui University of Finance & Economics;2.School of Statistics and Applied Mathematics,Anhui University of Finance & Economics,Bengbu 233030, China)
For short-term power load forecasting problem, using MATLAB software to establish daily highest temperature, daily minimum temperature, daily average temperature and humidity of meteorological factors on the regression of power load forecasting model, the specific comparison shows the BP neural network with two kinds of NARX neural network regression prediction results, through the hidden layer of network parameters and the debugging for the appropriate improved BP neural network.
power load forecasting; meteorological factors; the BP neural network; the NARX neural network; MATLAB
2016-06-08
国家自然科学基金(11301001);安徽高等学校省级自然科学基金(KJ2013Z001);安徽财经大学校级重点研究项目(ACKY1402ZD).
黄宏运(1995-),男,安徽合肥人,主要从事金融学和数学建模方面的研究.
1672-2027(2016)03-0042-06
O29;TP183
A

