GaInAsP/InP阶梯量子阱中电子-电子的散射率

王海龙， 李 正， 胡 敏， 李士玲， 龚 谦

(1. 山东省激光偏光与信息技术重点实验室， 曲阜师范大学 物理工程学院， 山东 曲阜 273165;2. 中国科学院上海微系统与信息技术研究所 信息功能材料国家重点实验室, 上海 200050)



GaInAsP/InP阶梯量子阱中电子-电子的散射率

王海龙1*， 李 正1， 胡 敏1， 李士玲1， 龚 谦2

(1. 山东省激光偏光与信息技术重点实验室， 曲阜师范大学 物理工程学院， 山东 曲阜 273165;2. 中国科学院上海微系统与信息技术研究所 信息功能材料国家重点实验室, 上海 200050)

在有效质量近似下，利用打靶法和费米黄金定则计算出GaxIn1-xAsyP1-y/InP阶梯量子阱中两个及多个电子从第一激发态子带到基态子带的散射率及平均散射率。计算结果表明，电子-电子的散射率和平均散射率随Ga组分和阱宽的增大而升高，随As组分的增大而降低。散射率随电子初态能和外加电场强度的增大而降低，平均散射率随载流子浓度的增大而升高。电子温度对平均散射率的影响不明显，平均散射率随着电子温度的升高而稍微降低。

GaxIn1-xAsyP1-y/InP； 阶梯量子阱； 电子； 费米黄金定则； 散射率

1 引 言

低维半导体材料因为其独特的物理结构和特性，被广泛应用于各种光电子器件[1-3]。量子阱作为一种重要的低维半导体结构，具有独特的电学和光学性质[4-6]。其中，阶梯量子阱(SQW)由于阱中阶梯的存在破坏了阱结构的对称性，这可以增强激光器的自发辐射复合率和光学增益，其较强的量子尺寸效应和应变效应能够减小价带中载流子的有效质量，降低态密度，在新型半导体光电子器件制作中有重要应用[7-11]。GaInAsP/InP异质结构由于不含Al组分，其性能相对稳定，并且可以在较大的范围内对组分进行调节，基于GaInAsP材料的激光器的激射波长在1.1～1.65 μm范围内可任意选择，包含了用于光通信的1.3 μm与1.55 μm两个低色散、低损耗窗口，在通信领域中占有重要地位[12-14]。

载流子的散射是一种重要的物理过程，它会限制载流子在半导体材料中的漂移速度和迁移率，从而影响半导体器件的工作性能。因此，对载流子散射的研究具有重要的意义，近年来一直是研究热点[15-19]。在以前的工作中，我们研究了Ga1-xInxNyAs1-y/GaAs量子阱中电子-纵向光学声子的散射率[19]，目前对GaxIn1-xAsyP1-y/InP阶梯量子阱中电子-电子散射率的研究还未见报道。本文在有效质量近似下，利用打靶法和费米黄金定则计算了GaxIn1-xAsyP1-y/InP 阶梯量子阱中两个及多个电子从第一激发态子带到基态子带的散射率和平均散射率。计算结果可以对基于阶梯量子阱结构以及GaxIn1-xAsyP1-y/InP材料的光电器件的设计提供一定的理论依据。

2 理论模型与方法

一个一般的不显含时间的薛定谔方程可以写为其中m*和ψ(z)分别为电子的有效质量和波函数，V(z)为一维限制势。

在一阶导数定义的基础上，式(1)可以写为

(2)

上式需满足以下标准边界条件：

(3)

式(2)被称为打靶方程。在本文中，电子的基态能、第一激发态能以及对应的波函数都由式(2)计算得到。

定义外加电场沿着阱的生长方向，则外加电场下阱中的限制势V(z)变为V(z)-eF(z-z0), 其中，F为外加电场强度，e为元电荷，位置z0代表外加电场的原点，这里选取阱的中心。将外加电场下阱中的限制势代入到公式(2)中，可计算出外加电场下电子的基态能、第一激发态能以及对应的波函数。

(4)

(5)

其中ε为材料的介电常数，r为两电子间的距离。

量子阱中，电子的波函数为

(6)

其中，k为波矢，rxy为x-y平面内的位置矢量。

把式(5)、(6)代入式(4)，其中的矩阵元的形式变为

(7)

其中，初态子带下标是“i”和“j”，末态子带下标为“f”和“g”。

利用库仑势的二维傅里叶变换，上式变为

(8)

(9)

将表征矩阵元素的式(8)代入式(4)，可得

(10)

将末态波矢的和转换为积分，并引入分布函数Pj,f,g(ki,kf,kg)，可得

(11)

上式为一个有特定波矢ki的电子和另一个电子的散射率表达式。

关于kj的积分可以通过有效的平面极坐标来求解，并且沿着长度kij和在ki与kj之间的角度α周围进行积分，最终可得两个电子之间电子-电子的散射率：

(12)

实际情况下初态子带中应有多个电子，因此需要通过费米-狄拉克分布来对散射率求平均，即

(13)

其中引入上标k是为了表明这是与波矢ki有关的平面内的动能。上式的分母可以表示为

(14)

由于平面内电子能量可以用一个波矢来表示，并且

(15)

(16)

因此平均散射率为

(17)

3 结果与讨论

本文计算的阶梯量子阱结构示意图如图1所示，势垒为200nm的InP，阶梯层为10nm的Ga0.07In0.93As0.15P0.85，阱为不同Ga、As组分的GaxIn1-xAsyP1-y。GaxIn1-xAsyP1-y的能带偏移率取67∶33，禁带宽度和电子的有效质量分别为[20]：

Eg=1.35-y+1.4x-0.33xy-

(0.758-0.28y)x(1-x)-

(0.101+0.109x)y(1-y) eV,

(18)

0.0948y+0.0391(1-x)y]m0,

(19)

其中，m0为真空中自由电子的质量。

Fig.1StructureofGaxIn1-xAsyP1-ysteppedQWforcalculation

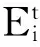
图2 阱中不同组分下电子-电子从第一激发态子带到基态子带的散射率随电子初态能的变化情况。 (a) 不同的As组分；(b)不同的Ga组分。

Fig.2Scatteringrateforelectron-electroninitiallyinthefirstexcitedsubbandandfinallyinthegroundsubbandasafunctionoftheinitialelectronenergywithdifferentalloycompositionsinquantumwell. (a)DifferentAscompositions. (b)DifferentGacompositions.

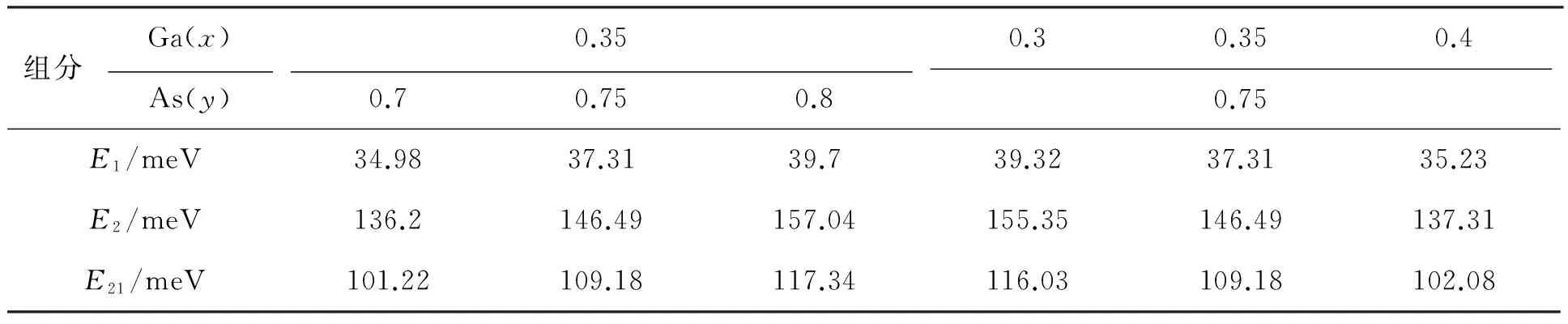
表1 阱宽为10 nm的阱中不同组分下电子的基态能E1、第一激发态能E2及子带能级差E21

Tab.1GroundstateenergyE1,firstexcitedstateenergyE2andsubbandseparationE21oftheelectronwithdifferentalloycompositionsinquantumwellfor10nmwellwidth

组分Ga(x)0.350.30.350.4As(y)0.70.750.80.75E1/meV34.9837.3139.739.3237.3135.23E2/meV136.2146.49157.04155.35146.49137.31E21/meV101.22109.18117.34116.03109.18102.08

图3给出了在阱中不同的Ga和As组分下，两个电子从第一激发态子带到基态子带的平均散射率随电子温度的变化情况，其中阱宽取10 nm，载流子浓度取1010cm-2。从图中可以看出，当Ga的组分不变时，电子-电子的平均散射率随着As组分的增加而降低；而当As的组分不变时，电子-电子的平均散射率随着Ga组分的增加而升高。这与图2中电子-电子从第一激发态子带到基态子带的散射率随阱中组分的变化趋势相同，可见子带能级差E21越大，散射的转移能量越大，这同样会导致平均散射率降低。

图3 在阱中不同的组分下电子-电子从第一激发态子带到基态子带的平均散射率随电子温度的变化情况。(a) 不同的As组分；(b) 不同的Ga组分。

Fig.3 Mean scattering rate for electron-electron initially in the first excited subband and finally in the ground subband as a function of the electron temperature with different alloy compositions in quantum well. (a) Different As compositions. (b) Different Ga compositions.

图4和图5分别给出了阱宽对电子-电子从第一激发态子带到基态子带的散射率及平均散射率的影响，其中电子温度取300 K，阱中Ga与As的组分分别取0.35与0.75。图中电子-电子的散射率和平均散射率都随阱宽的增大而升高。这是因为阱中电子的基态能和第一激发态能会随着阱宽的增加而减小，其子带能级差E21也相应减小，导致散射的转移能量减小，因此散射率和平均散射率升高。可见阱宽对散射率和平均散射率的影响都是相同的。

图6给出了在不同的外加电场强度下阱中电子-电子从第一激发态子带到基态子带散射率随电子初态能的变化情况，其中阱宽取10 nm，阱中Ga与As的组分分别取0.35与0.75，电子温度取300 K。从图中可以看出，阱中电子-电子的散射率随着外加电场强度的增大而降低。这是因为两个或多个电子从第一激发态子带到基态子带间的散射都是对称散射，外加电场会加大对阶梯量子阱中限制势对称性的破坏，从而增强了非对称散射却同时削弱了对称散射，因此电子-电子的散射率随场强的增大而降低。且由表2可知，当电场强度大于20 kV/cm时，子带能级差随场强的增加有较为明显的增大，使得散射的转移能量增大，这个因素也会导致散射率降低。

图4 在不同的阱宽下阱中电子-电子从第一激发态子带到基态子带的散射率随电子初态能的变化情况

Fig.4 Scattering rate for electron-electron initially in the first excited subband and finally in the ground subband as a function of the initial electron energy with different well widths

Fig.5 Mean scattering rate for multiple electrons initially in the first excited subband and finally in the ground subband as a function of the well width

表2 在不同电场强度下阱宽为10 nm的阱中电子的子带能级差E21

Tab.2 Subband separationE21of the electron in quantum well with width of 10 nm under different intensities of applied electric field

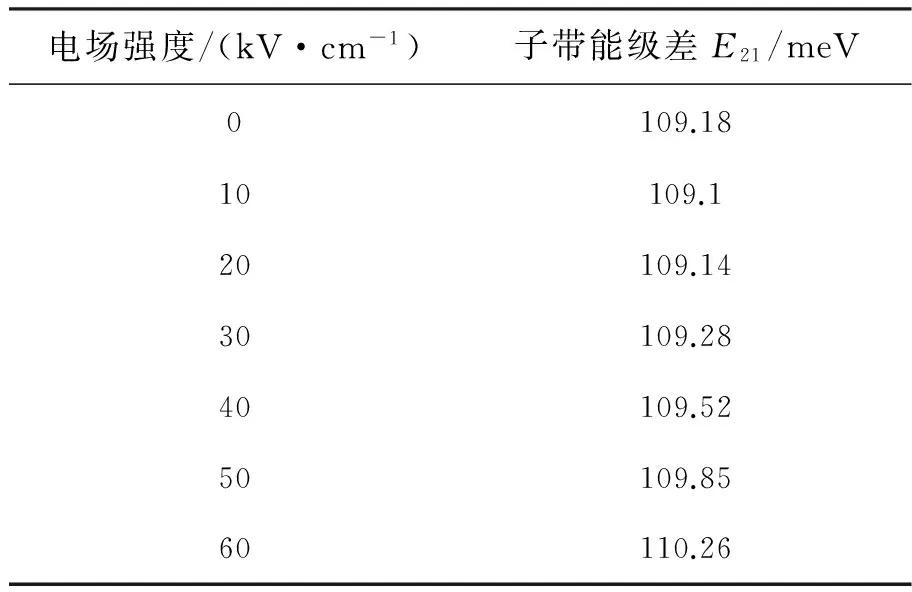
电场强度/(kV·cm-1)子带能级差E21/meV0109.1810109.120109.1430109.2840109.5250109.8560110.26

图7给出了阱中电子-电子从第一激发态子带到基态子带的平均散射率随载流子浓度N的变化情况，其中阱宽取10 nm，电子温度取300 K，阱中Ga、As的组分分别取0.35与0.75。从图中可以看出，电子-电子的平均散射率随着载流子浓度N的增加而升高。这是因为当Ga、As的组分、阱宽、垒宽、阶梯层宽度和电子温度都固定不变时，电子的基态能E1、第一激发态能E2以及子带能级差E21也都保持不变。在这种情况下，载流子浓度N越大，电子之间的联系越紧密，散射的能量转移也越容易发生，那么平均散射率也随之而升高。

图6 在不同的外加电场强度下阱中电子-电子从第一激发态子带到基态子带的散射率随电子初态能的变化情况

Fig.6 Scattering rate for electron-electron initially in the first excited subband and finally in the ground subband as a function of the initial electron energy under different intensities of applied electric field

Fig.7 Mean scattering rate for multiple electrons initially in the first excited subband and finally in the ground subband as a function of the carrier density

4 结 论

在有效质量近似下，利用打靶法计算出GaxIn1-xAsyP1-y/InP阶梯量子阱中电子的基态能、第一激发态能以及对应的波函数，并利用费米黄金定则求得两个及多个电子从第一激发态子带到基态子带的散射率及平均散射率随阱中不同的Ga、As组分、阱宽、电子初态能、电子温度、载流子浓度、外加电场强度的变化情况。计算结果表明：电子-电子的散射率和平均散射率随Ga组分和阱宽的增大而升高，随As组分和外加电场强度的增大而降低。散射率随电子初态能的增大而降低，平均散射率随载流子浓度的增大而升高。电子温度对平均散射率的影响不明显，平均散射率会随着电子温度的升高而略为降低。计算结果能够对基于阶梯量子阱结构和GaxIn1-xAsyP1-y/InP材料的光电子器件的设计提供一定的理论依据。

[1] LUDEWIG P, KNAUB N, HOSSAIN N,etal.. Electrical injection Ga(AsBi)/(AlGa)As single quantum well laser [J].Appl.Phys.Lett., 2013, 102(24):242115.

[2] GREADY D, EISENSTEIN G, IVANOV V,etal.. High speed 1.55 m InAs/InGaAlAs/InP quantum dot lasers [J].IEEEPhoton.Technol.Lett., 2014, 26(1):11-13.

[3] CHEN P, GONG Q, CAO C F,etal.. High performance external cavity InAs/InP quantum dot lasers [J].Appl.Phys.Lett., 2011, 98(12):121102.

[5] SOTHMANN B, SNCHEZ R, JORDAN A,etal.. Powerful energy harvester based on resonant-tunneling quantum wells [J].NewJ.Phys., 2013, 15:095021.

[6] JIANG L M, WANG H L, WU H T,etal.. Electronic states of a shallow hydrogenic donor impurity in different shaped semiconductor quantum wells [J].Commun.Theor.Phys., 2009, 51(6):1135-1138.

[7] YANG C C. High performance multiple stepped quantum well resonant microwave devices [J].Electron.Lett., 2006, 42(25):1485-1487.

[8] ZHAO H P, TANSU N. Optical gain characteristics of staggered InGaN quantum wells lasers [J].J.Appl.Phys., 2010, 107(11):113110.

[9] WEN Y, WANG Y P, WATANABE K,etal.. Effect of GaAs step layer on InGaAs/GaAsP quantum well solar cells [J].Appl.Phys.Express, 2011, 4(12):122301.

[10] WEN Y, WANG Y P, WATANABE K,etal.. Effect of GaAs step layer thickness in InGaAs/GaAsP stepped quantum-well solar cell [J].IEEEJ.Photovolt., 2013, 3(1):289-294.

[11] KHAN M A, PAVEL A A, ISLAM N． Intersubband transition in asymmetric quantum well Infrared photodetector [J].IEEET.Nanotechnol., 2013, 12(4):521-523.

[12] ARAI S, NISHIYAMA N, MARUYAMA T,etal.. GaInAsP/InP membrane lasers for optical interconnects [J].IEEEJ.Sel.Top.Quant.Electron., 2011, 17:1381-1387.

[13] OKUMURA T, KOGUCHI T, ITO H,etal.. Injection-type GaInAsP/InP membrane buried heterostructure distributed feedback laser [J].Appl.Phys.Lett., 2011, 4(4):042101.

[14] 王文娟，王海龙，龚谦，等．外电场对InGaAsP/InP量子阱内激子结合能的影响 [J]. 物理学报， 2013， 62(23):237104. WANG W J, WANG H L, GONG Q,etal.. External electric field effect on exciton binding energy in InGaAsP/InP quantum wells [J].ActaPhys.Sinica, 2013, 62(23):237104. (in Chinese)

[15] THÜRMER S, SEIDEL R, FAUBEL M,etal.. Photoelectron angular distributions from liquid water: effects of electron scattering [J].Phys.Rev.Lett., 2013, 111(17):173005.

[16] YAO J M, BENDER M, HEENEN P H. Beyond-mean-field study of elastic and inelastic electron scattering off nuclei [J].Phys.Rev. C, 2015, 91(2):024301.

[18] OVADYAHU Z. Suppression of inelastic electron-electron scattering in anderson insulators [J].Phys.Rev.Lett., 2012, 108(15):156602.

[19] 陈茜，王海龙，汪辉，等．Ga1-xInxNyAs1-y/GaAs量子阱中电子-LO声子的散射率 [J]. 物理学报, 2013, 62(20):226301. CHEN Q, WANG H L, WANG H,etal.. Electron-LO phonon scattering in Ga1-xInxNyAs1-y/GaAs quantum well [J].ActaPhys.Sinica, 2013, 62(20):226301. (in Chinese)

[20] HERBERT LI E. Material parameters of InGaAsP and InAlGaAs systems for use in quantum well structures at low and room temperatures [J].PhysicaE, 2000, 5:215-273.

王海龙(1971- ),男，山东莘县人，博士，教授，博士生导师，2000年于中国科学院半导体研究所获得博士学位,主要从事光通信、半导体光电子学等方面的研究。

E-mail: hlwang@mail.qfnu.edu.cn

Electron-electron Scattering Rate in GaInAsP/InP Stepped Quantum Well

WANG Hai-long1*， LI Zheng1， HU Min1, LI Shi-ling1, GONG Qian2

(1.ShandongProvincialKeyLaboratoryofLaserPolarizationandInformationTechnology,CollegeofPhysicsandEngineering,QufuNormalUniversity,Qufu273165,China;2.StateKeyLaboratoryofFunctionalMaterialsforInformatics,ShanghaiInstituteofMicrosystemandInformationTechnology,ChineseAcademyofSciences,Shanghai200050,China)

Within the framework of effective mass approximation, the scattering rate and the mean scattering rate for two electrons and multiple electrons initially in the first excited subband and finally in the ground subband in GaxIn1-xAsyP1-y/InP stepped quantum well were calculated adopting the shooting method and Fermi’s golden rule. The results show that the electron-electron scattering rate and the mean scattering rate increase with the increasing of Ga composition and well width, decrease with the increasing of As composition. The scattering rate decreases with the increasing of initial electron energy and intensity of applied electric field. The mean scattering rate increases with the increasing of carrier density. The electron temperature does not have great influence on the mean scattering rate, the mean scattering rate decreases slightly as the electron temperature rises. The calculated results can provide theory basis and guiding significance for the design of optoelectronic devices based on stepped quantum well and GaInAsP/InP material.

GaxIn1-xAsyP1-y/InP; stepped quantum well; electron; Fermi’s golden rule; scattering rate

1000-7032(2016)11-1408-07

2016-07-06；

2016-08-17

国家自然科学基金(61176065,61205055)； 山东省自然科学基金(ZR2014FM011)； 信息功能材料国家重点实验开放课题(SKL201307)资助项目

O471.1

A

10.3788/fgxb20163711.1408

*CorrespondingAuthor,E-mail:hlwang@mail.qfnu.edu.cn