Removingmixed noiseinlow ranktexturesbyconvex optimization

Xiao Liang()

©The Author(s)2016.This article is published with open access at Springerlink.com

Removingmixed noiseinlow ranktexturesbyconvex optimization

Xiao Liang1()

©The Author(s)2016.This article is published with open access at Springerlink.com

DOI 10.1007/s41095-016-0056-2 Vol.2,No.3,September 2016,267–276

This paper introduces a new low rank texture image denoising algorithm,which can restore low rank texture contaminated by both Gaussian and salt-and-pepper noise.The algorithm formulates texture image denoising in terms of solving a low rank matrix optimization problem.Simply assuming low rank is insufficient to describe the properties of natural images,causing high noise amplitudes which lead to unsatisfactory denoising results or serious loss of image details.Thus,in addition to the low rank assumption, the continuity of natural images is also assumed by the algorithm,by adding a total variation regularizer to the optimization objective function. We further give an effective algorithm to solve this optimization problem.By combining the low rank and continuity assumptions,the proposed algorithm overcomes the deficiencies of using either the low rank assumption or total variation regularization alone.Experiments show that our algorithm can effectively remove mixed noise in low rank texture images,and is better than existing algorithms in both its subjective visual effects and in terms of quantitative objective measures.

image denoising;low rank texture; total variation;convex optimization; augmented Lagrangian method

1 Introduction

Image denoising is an extensively studied problem in the image processing community and continues to attract researchers who aim to perform better restoration in the presence of noise. During the past few decades,many intelligent methods havebeen proposed to improve single-image denoising performance. From pixel level filtering methods, such as Gaussian filtering[1],bilateral filtering,and total variation regularization[2],to patch based filtering methods,such as non-local means[3], block-matching 3D filtering(BM3D)[4],and sparse representation [5],single-imagebased denoising performance has been greatly improved,with image details well recovered when the image is slightly noisy.As such filtering methods are widely used in computer vision,work has considered how to speed them up,e.g.,for the bilateral filter[6]and weighted median[7].Comprehensive overviews of image denoising methods can be found in Refs.[8,9].

Most of the approaches mentioned above consider the input image as an ordinary signal,taking the image as a vector or a set of patches. They do explicitly utilize internal structural information in the image. However,a typical 3D scene of an artificial environment is rich in regular structures. For instance,in an urban environment,the scene istypically filled with man-madeobjectsthat have parallel edges,right-angled corners,regular shapes,symmetric structures,and repeated patterns. Developing algorithms targeted to such images is necessary.In this paper,we mainly study images or textures with low rank structure(see Fig.1 for examples).A rigorous definition[10]of low rank texture is given in Section 2.

Fig.1 Representative examples of low rank textures.These provide initial images for Figs.3–5.

Recently,low rank matrix denoising algorithms have been widely studied[11–15].The traditional, image denoising algorithms based on low rank matrix recovery only have the low rank constraint. When Gaussian noise becomes too large,these algorithms produce unsatisfactory denoising results, with serious loss of image details. The reason is partially because that most algorithms use the nuclear norm of the matrix to approximate its rank, in order to get a soluble convex object function, which brings the following problem:as the amplitude of the Gaussian noise increases,the energy of the matrix is compressed more and more seriously.In order to solve the problem of texture image denoising in a mixed noise model,we propose a new algorithm call LRTD(low rank texture denoising)in this paper.

LRTD formulates texture image denoising in terms of solving a low rank matrix optimization problem.Because the low rank assumption is not sufficient by itself to describe the properties of natural images[16],high noise amplitudes will lead to unsatisfactory denoising results with serious loss of image details.Thus,in addition to the low rank assumption,we also assume image continuity in the algorithm,by adding a total variation regularizer to the optimization objective function.An effective algorithm to solve this optimization problem is also given in the paper. By combining the low rank assumption and the continuity assumption, the proposed LRTD algorithm can overcome the deficiencies of assuming low rank assumption or using total variation regularization alone. The algorithm can effectively remove mixed noise in low rank texture images,and is better than existing algorithms in terms of both subjective visual effects and objective quantitative measurements.

2 Definition of low rank textures

In this paper,we consider a 2D texture as a function I0(x,y),defined on ℝ2.We say that I0is a low rank texture if the family of one-dimensional functions {I0(x,y0)|y0∈ℝ}span a finite low-dimensional linear subspace:

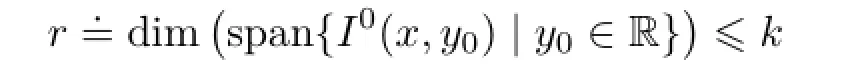
for some small positive integer k.If r is finite,then we refer to I0as a rank-r texture.Figure 1 shows some ideal low rank textures.To a large extent,the notion of low rank texture unifies many conventional local features.Using this definition,it is easy to see that images of regular symmetric patterns always lead to low rank textures.Thus,the notion of low rank texture encompasses a much broader range of“features”or regions than corners and edges.

3 Problem formulation

Before we statistically analyze image denoising,we first define our image formation model:

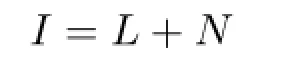
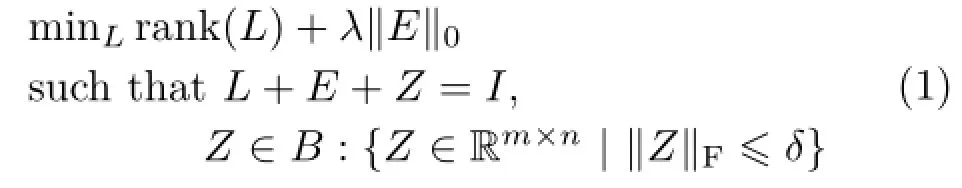
where‖E‖0denotes the number of non-zero entries in E,‖·‖Fdenotes the Frobenius norm,δ>0 is a Gaussian noise intensity parameter,and λ is a weighting parameter which trades off the rank and sparsity of the recovered image.In the above problem,both the rank function and the l0norm can be replaced by convex surrogates[17]:the matrix nuclear norm1The nuclear norm of a matrix is the sum of all its singular values.‖L‖∗for rank(L)and the l1norm2The l1norm is the sum of absolute values.‖E‖1for‖E‖0,respectively.Thus,we end up with the following optimization problem:

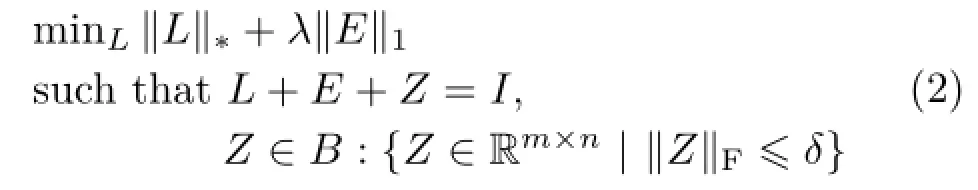
Formulation(2)utilizes the low rank nature of the image and the sparsity of the impulsive noise E.But as noted in Ref.[16],while being low rank is a necessary condition for most regular, structured images,it is certainly not sufficient.We need other priors to model additional structures in

the natural image.Moreover,because the nuclear norm is an approximation to the rank of a matrix, when the noise amplitude is large,formulation(2) leads to over-compression of the nuclear norm[18], causing the total energy of the denoised image to significantly decrease:the picture becomes darker; see for example the fourth column of Fig.5.Thus,to take into account the piecewise smooth continuity of a natural image,we add a total variation regularizer to the optimization problem:

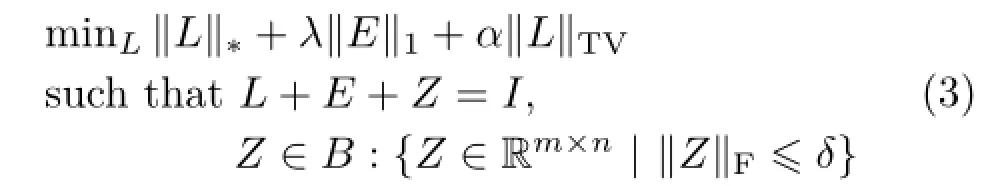
where‖L‖TV= ‖DxL‖1+‖DyL‖1is the total variation regularizer,in which Dxand Dyare first order forward finite-difference operators in horizontal and vertical directions respectively.Their definitions are

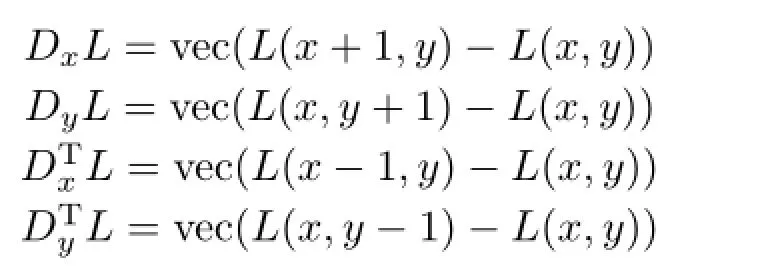
with periodic boundary conditions;vec(·)represents the vectorization operator.

4 Denoising by convex optimization

To solve the convex optimization problem in Eq.(3), we use the alternating direction method(ADM)[19], as it has been proven to be one of the fastest algorithms for solving various low rank matrix completion and recovery problems.To be able to adopt the ADM method to our problem,we need to make our objective function separable. Thus we introduce three auxiliary variables Cx,Cy,and

W,which turns the optimization problem into the following:

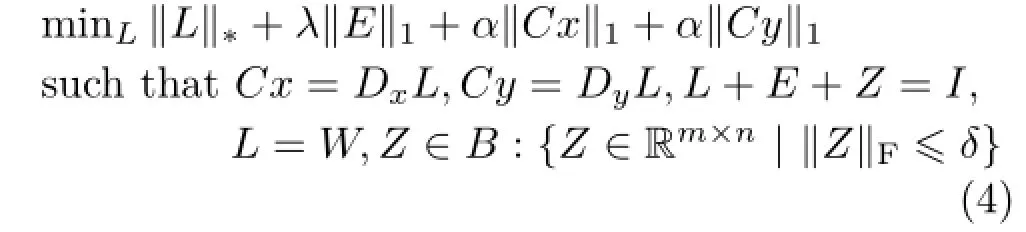
In formulation(4),the augmented Lagrangian function is defined as

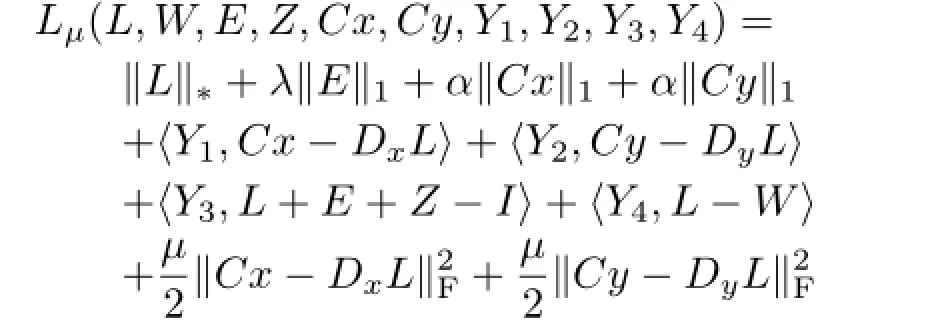
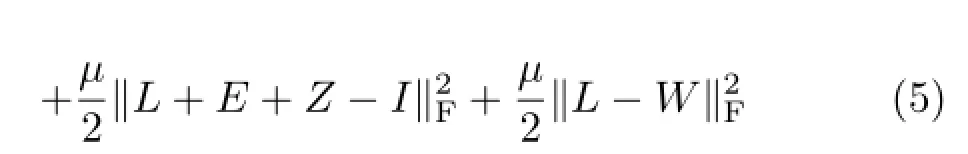
where L,W,E,Z,Cx,Cy are the unknown variables,Y1,Y2,Y3,Y4are Lagrange multipliers, andµ>0 is a penalty parameter;〈·,·〉indicates inner product.The resulting classic ADM iteration scheme for our problem is given by

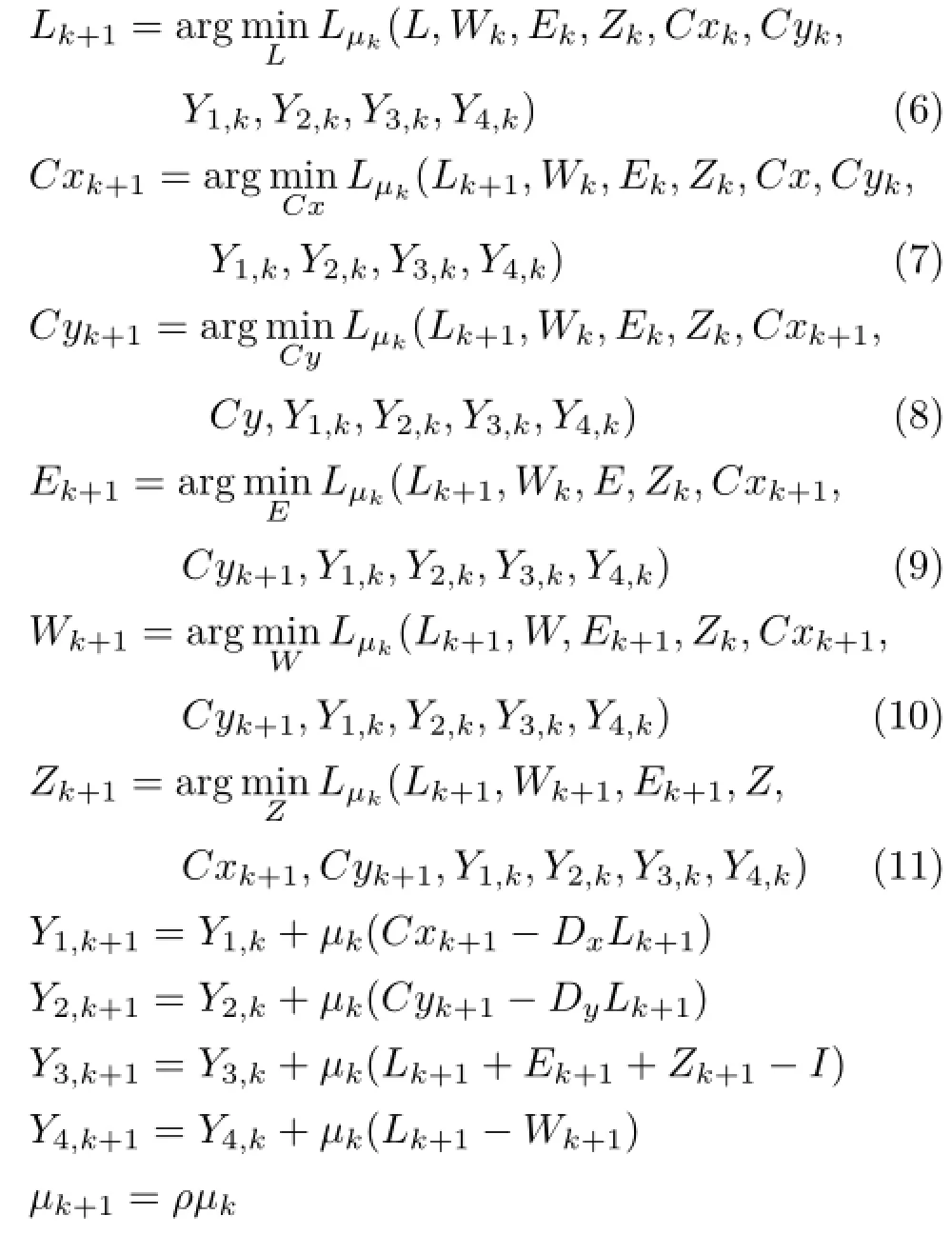
where ρ>1 is a constant. We now focus on efficiently solving the first six steps of the above iterative scheme.

1)Solving Eq.(6)

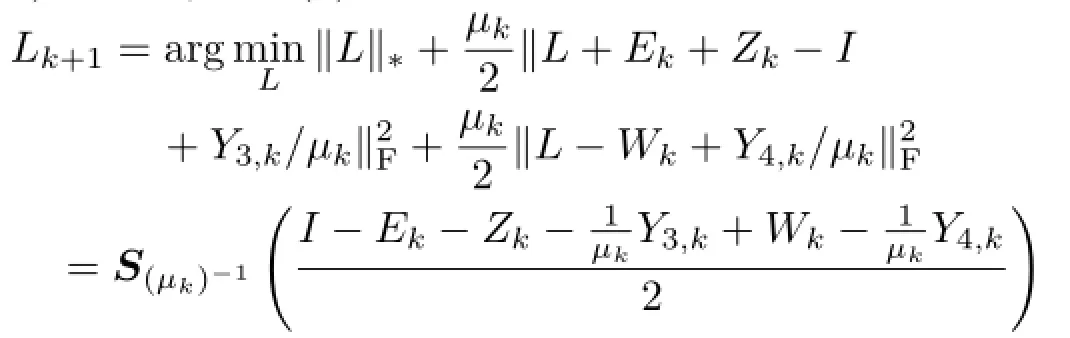
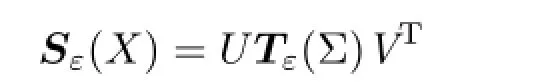
in which UΣVTistheSVD (singularvalue decomposition)of X,and T[·]represents the softthresholding operator defined for scalars as follows:

for ε≥0;it is extended to vectors and matrices by applying it elementwise.

2)Solving Eqs.(7)–(9)

Each of these three variables has closed form solutions,as follows:

3)Solving Eq.(10)

Here W also has a closed form solution:

where Id is the identity matrix.Then we use Fourier transform to solve W[2]:

where F denotes the 2D Fourier transform operator. The denominator on the right hand side of Eq.(12)is independent of the iteration number k,and so can be precalculated outside the main loop.Therefore,the complexity of solving Eq.(12)is the complexity of one 2D Fourier transform and one inverse 2D Fourier transform.

4)Solving Eq.(11)

Following Ref.[13],we write

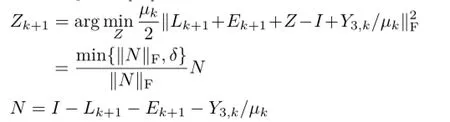
Algorithm 1 gives pseudocode of the overall LRTD algorithm.

5 Results

In this section we compare our LRTD algorithm with existing approaches.All experiments were performed using MATLAB on a laptop with a 2.30GHz processor and 8GB of RAM.

We select a set of parameters with the best overall performance for λ and α in our algorithm;LRTD is not sensitive to parameterµ0.ρ=max(1.4−

σ/600,1.2)is related to noise intensity σ. The greater the σ,the smaller the ρ.

Algorithm 1:ADM algorithm for solving problem(4) Input:Input image I∈ℝm×n,parameters λ>0,α>0. Initialize:k=0,L0=I,E0=0,Z0=0,W0=0,Cx=DxI,Cy=DyI,Y1,0=0,Y2,0=0,Y3,0=0,Y4,0=0, µ0>0,ρ>1. WHILE‖Lk+1−Lk‖2/‖Lk‖2≥tolerance DO Lk+1=S(µk)−1?I−Ek−Zk−1µkY3,k+Wk−1µkY4,k/2)?; Cxk+1=Tα/µk(DxWk−Y1,k/µk); Cyk+1=Tα/µk(DyWk−Y1,k/µk); Ek+1=Tλ/µk(I−Lk+1−Zk−Y3,k/µk); Wk+1=F−1?F[DTx(Cxk+1+Y1,k/µk)+DTy(Cyk+1+Y2,k/µk)+L−Y4,k/µk] F[Id+DTxDx+DTyDy] ?;‖N‖F N; Y1,k+1=Y1,k+µk·(Cxk+1−DxLk+1); Y2,k+1=Y2,k+µk·(Cyk+1−DyLk+1); Y3,k+1=Y3,k+µk·(Lk+1+Ek+1+Zk+1−I); Y4,k+1=Y4,k+µk·(Lk+1−Wk+1); µk+1=ρµk; END WHILE Output:Solution(L,E,W,Z,Cx,Cy)to problem(4). Zk+1=min{‖N‖F,δ}

5.1 Comparison with othermixed noise removal methods

In this paper we consider image denoising problems with mixed noise,in which the image is contaminated by both Gaussian white noise and salt-and-pepper noise. Somewellknown denoising methods such as BM3D work very well to restore images contaminated by pure Gaussian noise,but are completely unable to deal with salt-and-pepper noise[21].Thus,we only compare our LRTD method with three other noise removal methods[13,22,23] specifically designed for mixed noise.

Following their papers,the parameter settings used were:for Ref.[22],β2=0.00002,tol=10−4, η=1;for Ref.[23],outPer=sr,blocksize=[8,8], stepsize=[2,2];for Ref.[13],η=1.3,β=0.13β0. Besides visual comparison of the results,peak signal to noise ratio(PSNR)was measured to quantitatively evaluate the quality of the restoration results.Given an image L∗∈[0,255]m×n,the PSNR of its estimated L is defined as

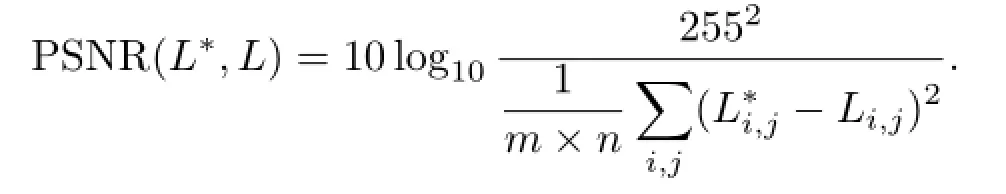
A quantitative comparison is shown in Fig.2. Here,we used the image in Fig.1(c)for testing. The percentage of salt-and-pepper noise pixels in the image is denoted by sr(salt-and-pepper noise ratio), while the standard deviation of the white Gaussian noise is denoted by σ.Figure 3(a)shows how PSNR varies for the denoised images as the salt-and-pepper noise ratio sr varies from 0 to 100%with fixed Gaussian noise σ=10;Fig.3(b)shows how PSNR of denoised images varies as the standard deviation of the Guassian noise σ varies from 0 to 60 with a fixed salt-and-pepper noise percentage sr=10%.

Further quantitative results for the four algorithms were obtained using input images generated by adding salt-and-pepper noise with different levels (sr=15%,30%,45%)mixed with Gaussian noise with different levels(σ=5,15,30,60)to the textures shown in Fig.1.The PSNR values of the restoration results of these methods are summarized in Table 1. Figures 3–5 give qualitative comparisons;the original images in these experiment are shown in Fig.1.We can see from these results that LRTD works better on low rank texture images than previous algorithms.

From Fig.2 and Table 1 we can see that LRTD's ability to process salt-and-pepper noise is very good. In low Gaussian noise environments(σ＜10),as the percentage of salt-and-pepper noise increases from 0%to 60%,the PSNRs of our image restoration results do not decrease significantly,and are always more than 30dB.However,the LRTD algorithm is more sensitive to Gaussian noise.As Gaussian noise increases to about σ=60,results shown in Fig.5 display the excessive compression issue caused by use of convex surrogates for the rank function.Although the structure of the restored image is still quite good, due to the compression of the overall energy of the input image during the optimization process,the resulting PSNR decreases significantly.

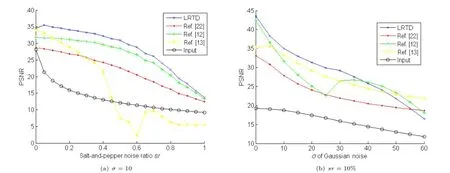
Fig.2 Variation of PSNR with varying amounts of salt-and-pepper noise and Gaussian noise.(a)σ=10,sr varying from 0 to 100%;(b) sr=10%,σ varying from 0 to 60.

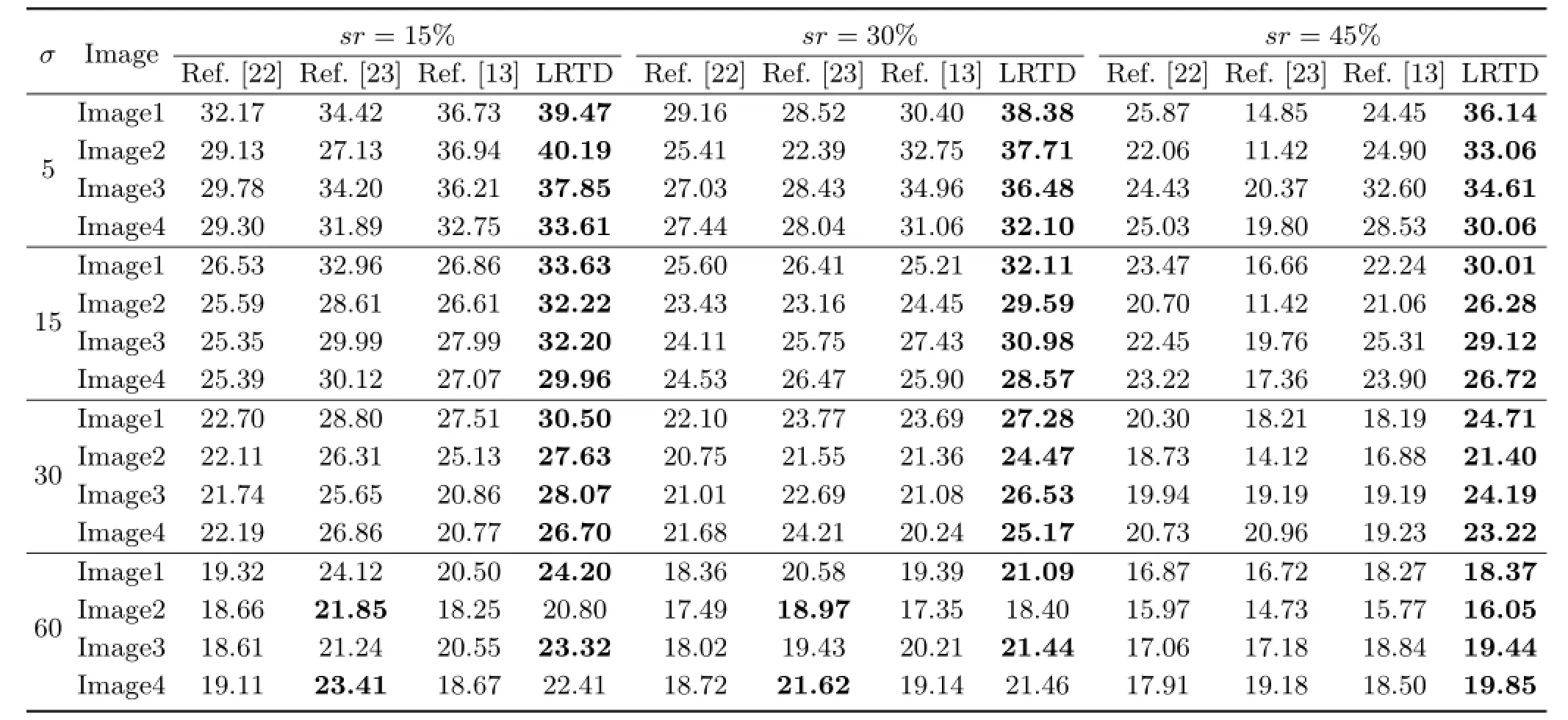
Table 1 Comparison with other mixed noise removal methods,showing PSNR values for varying amounts of salt-and-pepper and Gaussian noise

The results in this subsection demonstrate that our LRTD denoising method can effectively remove mixed noise in low rank texture images,and works better than other existing algorithms.Addition of the TV regularizer to the optimization objective function has a good effect on avoiding the problem of excessive compression.Our LRTD shows significant improvement compared to the simple low rank optimization algorithm[13].

5.2 Computation time

We performed a further experiment to test the convergence performance of LRTD.Let I=L∗+E∗+Z∗be the noisy data matrix,where L∗and E∗are the low rank and sparse components to be recovered. We generated a rank 2 checkerboard image as L∗∈ℝ320×320.The support Ω of the impulsive noise E∗(sparse but large)was chosen uniformly at random, and the non-zero entries of E∗were i.i.d.uniform in the interval[−500,500].

As our aim was to test running speed and convergence of LRTD,we set σ=0;this differs from the mixed noise used in the earlier tests as there is no Gaussian noise.In this case,the algorithm can converge to the ground truth noiseless matrix L∗.

Here we compare our method with another low rank matrix recovery algorithm ASALM[13].The objective function of ASALM is given in Eq.(2):the only difference between ASALM with our LRTD is that ASALM lacks the TV regularizer.Following their paper,we set the parameters for ASALM to η=1.3,β=0.13β0.Table 2 shows that LRTD is slower than ASALM.However,LRTD performs better in denoising.We believe the trade-off to be acceptable.

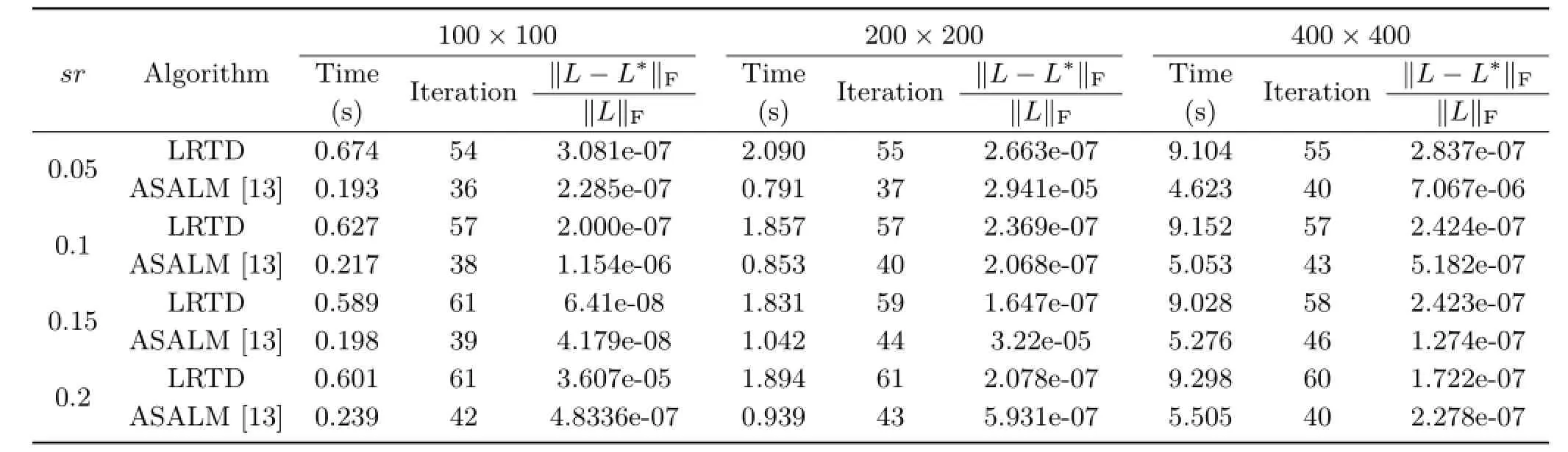
Table 2 Computation time and number of iterations

Fig.3 Qualitative comparison of results of various methods(1).Left to right:input noisy image with σ=10,sr=10%,denoising results of Ref.[22],KALS[23],ASALM[13],and our denoising result.

6 Conclusions and discussion

This paper introduced a new low rank texture image denoising algorithm,which can restore low rank texture contaminated by both Gaussian and salt-and-pepper noise. Our method directly uses raw pixel values of the image as the matrix and models texture image denoising as a low rank matrix optimization problem. Besides the low rank assumption,we also utilize the assumption of continuity of natural images,by adding a total variation regularizer to the optimization objective function. Our results demonstrate that the TV regularizer indeed helps low rank texture denoising.

Through extensive experiments,we have shown that our LRTD method works better than existing algorithms both in subjective visual terms and through objective quantitative measures.

Although our algorithm works robustly under a broad range of conditions and for a wide range of regular textures,it may fail if the conditions are too challenging or the assumptions are violated.Figure 6 shows some such cases.The denoising results in Fig.6(c)and Fig.6(e)are reasonable but not perfect. As mentioned earlier in Section 1,our algorithm is not designed to work on random textures.Although there has been work in the literature showing that it is possible to get a reasonable denoised result for

such examples as grass lawns,our algorithm is not designed to handle such cases.LRTD is effective for regular symmetric textures,but not for random textures which normally have high rank matrices.

Fig.4 Qualitative comparison of results of various methods(2).Left to right:input noisy image with σ=15,sr=45%,denoising results of Ref.[22],KALS[23],ASALM[13],and our denoising result.

Clearly,a natural image of low rank texture may be deformed by the camera projection and undergoes a certain domain transformation (say affine or projective). The transformed texture,viewed as a matrix,in general is no longer low rank in the image domain.Nevertheless,by utilizing advanced convex optimization tools[10]from matrix rank minimization,we can recover a low rank texture from the deformed image and the associated deformation. As TILT(transform invariant low rank texture)[10] uses image interpolation during its iterations,simply running LRTD on TILT results would hurt image performance.Finding how to combine TILT with LRTD to enable a wider range of applications would be valuable future work.

Acknowledgements

We sincerely appreciate Zhouchen Lin and Xin Tong's help with valuable suggestions and comments for this paper.

[1]Rank,K.;Unbehauen,R.An adaptive recursive 2-D filter for removal of Gaussian noise in images.IEEE

Transactions on Image Processing Vol.1,No.3,431–436,1992.

Fig.5 Qualitative comparison of results of various methods(3).Left to right:input noisy image with σ=60,sr=10%,denoising results of Ref.[22],KALS[23],ASALM[13],and our denoising result.

Fig.6 Examples with decreasing regularity and increasing randomness.(a),(c),and(e)input noisy images,with σ=10,sr=10%;(b), (d),and(f)denoising results and their PSNRs.

[2]Chan,S.H.;Khoshabeh,R.;Gibson,K.B.;Gill,P.E.; Nguyen,T.Q.An augmented Lagrangian method for total variation video restoration.IEEE Transactions on Image Processing Vol.20,No.11,3097–3111,2011.

[3]Buades,A.;Coll,B.;Morel,J.-M.A non-local algorithm for image denoising.In:Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Vol.2,60–65,2005.

[4]Dabov,K.;Foi,A.;Katkovnik,V.;Egiazarian, K.Image denoising by sparse 3-D transform-domain

collaborative filtering.IEEE Transactions on Image Processing Vol.16,No.8,2080–2095,2007.

[5]Afonso,M.V.;Sanches,J.M.R.Blind inpainting using l0and total variation regularization.IEEE Transactions on Image Processing Vol.24,No.7, 2239–2253,2015.

[6]Gastal, E.S.L.; Oliveira, M.M.Adaptive manifoldsforreal-timehigh-dimensionalfiltering. ACM Transactions on Graphics Vol.31,No.4,Article No.33,2012.

[7]Zhang,Q.;Xu,L.;Jia,J.100+ timesfaster weighted median filter(WMF).In:Proceedings of IEEE Conference on Computer Vision and Pattern Recognition,2830–2837,2014.

[8]Buades,A.;Coll,B.;Morel,J.-M.A review of image denoising algorithms,with a new one.SIAM Journal on Multiscale Modeling and Simulation: A SIAM Interdisciplinary Journal Vol.4,No.2,490–530,2005.

[9]Chatterjee,P.;Milanfar,P.Is denoising dead?IEEE Transactions on Image Processing Vol.19,No.4,895–911,2010.

[10]Zhang,Z.;Ganesh,A.;Liang,X.;Ma,Y.TILT: Transform-invariant low-rank textures.International Journal of Computer Vision Vol.99,No.1,1–24,2012.

[11]Dong,W.;Shi,G.;Li,X.Nonlocal image restoration with bilateralvariance estimation: A low-rank approach.IEEE Transactions on Image Processing Vol.22,No.2,700–711,2013.

[12]Shabalin,A.A.;Nobel,A.B.Reconstruction of a lowrank matrix in the presence of Gaussian noise.Journal of Multivariate Analysis Vol.118,No.5,67–76,2013.

[13]Tao,M.;Yuan,X.Recovering low-rank and sparse components of matrices from incomplete and noisy observations.SIAM Journal on Optimization Vol.21, No.1,57–81,2011.

[14]Zhang,Y.;Liu,Y.;Li,X.;Zhang,C.Salt and pepper noise removal in surveillance video based on low-rank matrix recovery.Computational Visual Media Vol.1, No.1,59–68,2015.

[15]Zhou,Z.;Li,X.;Wright,J.;Cand`es,E.J.;Ma,Y. Stable principal component pursuit.In:Proceedings of IEEE International Symposium on Information Theory,1518–1522,2010.

[16]Liang,X.;Ren,X.;Zhang,Z.;Ma,Y.Texture repairing by unified low rank optimization.Journal of Computer Science and Technology Vol.31,No.3,525–546,2016.

[17]Cand`es,E.J.;Li,X.;Ma,Y.;Wright,J.Robust principal component analysis?Journal of the ACM Vol.58,No.3,Article No.11,2011.

[18]Wang,Z.;Zhang,J.;Chen,G.Mixture noise image denoising using reweighted low-rank matrix recovery. Compuer Science Vol.43,No.1,298–301,2016.(in Chinese)

[19]Lin,Z.;Ganesh,A.;Wright,J.;Wu,L.;Chen,M.; Ma,Y.Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix.Technical Report.University of Illinois at Urbana-Champaign, 2009.

[20]Cand`es,E.J.;Plan,Y.Matrix completion with noise. Proceedings of the IEEE Vol.98,No.6,925–936,2010.

[21]Djurovi´c,I.BM3D filter in salt-and-pepper noise removal.EURASIP Journal on Image and Video Processing Vol.2016,13,2016.

[22]Cai,J.-F.;Chan,R.H.;Nikolova,M.Fast twophase image deblurring under impulse noise.Journal of Mathematical Imaging and Vision Vol.36,46–53, 2010.

[23]Wang,Y.;Szlam,A.;Lerman,G.Robust locally linear analysis with applications to image denoising and blind inpainting.SIAM Journal on Imaging Sciences Vol.6, No.1,526–562,2013.

Xiao Liang iscurrently a Ph.D. student in computer science and technology at the Institute for Advanced Study in Tsinghua University,Beijing, China. Her adviser is Prof. Harry Shum.She received her B.E.degree in electronic engineering from Tsinghua University. During herstudy,she interned at Microsoft Research Asia for over four years. Her research interests include texture processing,3D computervision and sparsity,and low rank matrix recovery.

Open Access The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License(http:// creativecommons.org/licenses/by/4.0/), which permits unrestricted use,distribution,and reproduction in any medium,provided you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons license,and indicate if changes were made.

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript,please go to https://www. editorialmanager.com/cvmj.

1 Institute for Advanced Study,Tsinghua University, Beijing100084,China. E-mail: liangx04@mails. tsinghua.edu.cn().

Manuscript received:2016-04-22;accepted:2016-05-25