Skeleton-based canonical forms for non-rigid 3D shape retrieval

David Pickup(),Xianfang Sun,Paul L.Rosin,and Ralph R.Martin

©The Author(s)2016.This article is published with open access at Springerlink.com

Skeleton-based canonical forms for non-rigid 3D shape retrieval

David Pickup1(),Xianfang Sun1,Paul L.Rosin1,and Ralph R.Martin1

©The Author(s)2016.This article is published with open access at Springerlink.com

DOI 10.1007/s41095-016-0045-5 Vol.2,No.3,September 2016,231–243

The retrieval of non-rigid 3D shapes is an important task.A common technique is to simplify this problem to a rigid shape retrieval task by producing a bending-invariant canonical form for each shape in the dataset to be searched.It is common for these techniques to attempt to“unbend”a shape by applying multidimensional scaling(MDS)to the distances between points on the mesh,but this leads to unwanted local shape distortions.We instead perform the unbending on the skeleton of the mesh,and use this to drive the deformation of the mesh itself.This leads to computational speed-up,and reduced distortion of local shape detail.We compare our method against other canonical forms:our experiments show that our method achieves state-of-the-art retrieval accuracy in a recent canonical forms benchmark,and only a small drop in retrieval accuracy over the state-of-the-art in a second recent benchmark,while being significantly faster.

canonical forms;shape retrieval;skeletons; pose invariance

1 Introduction

The task of example-based retrieval of non-rigid objects is both a key problem to solve and a challenging one.Upsurging numbers of 3D shape collections are being created,so the ability to search these collections is an increasingly important task. There have been many successes in the retrieval of rigid objects,with methods such as view-basedtechniques proving very successful[1].The problem is that many of these techniques cannot be applied to non-rigid shape retrieval.To address this issue Elad and Kimmel[2]proposed a bending-invariant 3D embedding of a mesh,called a canonical form.The canonical form of a mesh effectively standardises its pose,and therefore,if a canonical form is computed for each shape in a dataset,the non-rigid retrieval problem can be turned into a rigid retrieval problem. This means that any of the wide range of rigid shape retrieval methods available are then able to perform retrieval on this data.There are two issues with the canonical form method of Elad and Kimmel.The first is that it requires the geodesic distance to be computed between all pairs of vertices,which has a super-quadratic computational complexity. The second issue is that small scale local details of shapes are lost in the canonical form.

In this paper we address both issues by applying the method by Elad and Kimmel to the skeleton of the mesh,rather than to the mesh itself.The pose of the mesh is then deformed to agree with the pose of the resulting canonical skeleton.This is far more efficient,because the skeleton of a mesh contains far fewer vertices than the mesh itself,resulting in far fewer geodesic distance computations.Fewer shape details are distorted,because the method effectively produces a set of canonical angles at the articulated joints of the shape,and shape deformations are localised to these joint regions.This leads to an increased retrieval performance on a recent canonical forms benchmark[3].

The structure of our paper is as follows.Section 2 outlines related work in this area,Section 3 describes the technical details of our method,Section 4 presents the results of our experiments,and we draw conclusions in Section 5.

2 Related work

Many works aim to solve the retrieval problem for rigid shapes,using e.g.,lightfield descriptors[4]and spin images[5].We refer readers to Refs.[1]and[6] for detailed reviews of this field of research.

In recent years further research has concentrated on the problem of retrieving non-rigid models. Several methods are based on extracting local features from a mesh to compute a shape descriptor [7],including meshSIFT[8],conformal factors[9], area projection transforms[10],and heat kernal signatures[11].Computing histogramsoflocal features has proven to perform very well in recent retrieval benchmarks[12,13].

Graphs have also been used as shape descriptors. Hilaga et al.[14]used multiresolution Reeb graphs to match topology between 3D shapes,while Sfikas et al.[15]proposed formulating a graph based on conformal factors[9].

Matching global information about 3D shapes hasalso proved successful.Reuteretal.[16] demonstrated that the Laplace–Beltrami spectrum can be used as a shape descriptor,which they called ShapeDNA.Various global descriptors can also be extracted from the geodesic distance matrix of a mesh,as shown by Smeets et al.[17].

For a more detailed review of the latest non-rigid retrieval methods,we refer the reader to the recent SHREC benchmarks[12,13].

The use of canonical forms to normalise the pose of non-rigid shapes was first proposed by Elad and Kimmel[2].They used multidimensional scaling (MDS)to map the geodesic distances of a mesh into 3D Euclidean distances.Several variations to this method have been proposed.Shamai et al. [18]accelerated the classical MDS procedure using their proposed Nystr¨om multidimensional scaling framework.Lian et al.[19]attempted to preserve the features of a mesh by segmenting it and transforming each segment to its location in the canonical mesh computed using Elad and Kimmel's method,thus correcting some of the local shape distortions.Wang and Zha[20]speeded up the canonical form computation by only computing geodesic distances between all pairs of a set of detected feature points,and unbending the mesh by creating target axes used to align sets of geodesic contours.Pickup et al.[21]also used feature points, but restricted their number to the square root of the number of mesh vertices.They maximised the distance between pairs of these feature points whilst preserving the mesh's edge lengths.Boscaini et al.[22]proposed a method which assigns a repelling electrical charge at each vertex of the mesh to produce a canonical form.They were also able to correct certain small localised topological errors in the mesh,by cutting parts of the mesh which are likely to have been incorrectly joined.Their method is faster than Elad and Kimmel's,but still distorts local shape details.There is also work on parallelising or speeding up the computation of geodesic distances[23,24].Recent benchmarks[12, 25]have shown that using canonical forms along with the view-based shape retrieval method of Lian et al.[26]performs very competitively compared with other non-rigid retrieval approaches.

Our method differs from those above by normalising the pose of the shape's skeleton,rather than driving normalisation from mesh vertices.This causes less distortion of local shape details than other methods,whilst providing a practical level of efficiency.

3 Method

We first give an overview of the canonical form work by Elad and Kimmel[2]in Section 3.1,as our work builds upon this approach.We then detail our novel skeleton-based approach in Section 3.2.

3.1 Background

The canonical form work by Elad and Kimmel[2] transforms the mesh so that the geodesic distance between each pairofverticesaremapped to Euclidean distance.To accomplish this,they first compute the geodesic distances between all pairs of mesh vertices using the fast marching method[27]. Next,they use multidimensional scaling to calculate a new set of vertex positions,where the Euclidean distance between each pair of vertices is as close as possible to the computed geodesic distance.They show results with three different multidimensional scaling techniques,but the one which tends to provide the best results and which we use in ourwork, solvesthe multidimensionalscaling problem by minimising the following least-squares functional:

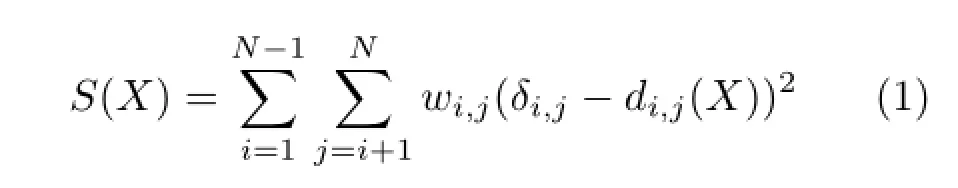
where N is the number of vertices,wi,jis the weighting coefficient,δi,jis the geodesic distance between vertices i and j of the original mesh,and di,jis the Euclidean distance between vertices i and j of the resulting canonical mesh X.This functional is minimised using the SMACOF(scaling by maximising a convex function)algorithm[28].

This method is computationally expensive,as the geodesic distances take O(N2logN)time to compute,andeachiterationoftheSMACOF algorithm takes O(N2)time.As this method works on the vertices of the mesh,it deforms details of its shape as well as normalising its pose.These details may be important in tasks such as shape retrieval.

3.2 Skeleton canonical forms

The purpose of computing a canonical form is to normalise the pose of a 3D object.The pose of an object can be defined as the articulation of the object's skeleton.This leads us to our method,which normalises the pose of an object by transforming it so that its skeleton is in a normalised pose.The stages of our method are depicted in Fig.1.We first extract the skeleton of the mesh (Section 3.2.1),then transform the skeleton into a canonical form(Section 3.2.2),and finally deform the mesh according to the skeleton transformation (Section 3.2.3).

3.2.1 Skeleton extraction

We first extract the mesh's skeleton using a method by Au et al.[29].It first contracts the mesh to a zerovolume skeletal shape using Laplacian smoothing. The mesh is then converted to a 1D curve skeleton by removing all mesh faces while preserving the skeletal topology.

The skeleton is then refined by merging junctions with neighbouring joints,if the merged junction has a better centeredness.A junction is defined as a joint attached to three or more bones.The centeredness of a junction is defined as the standard deviation of the distances between the junction's position and the position of each vertex assigned to that junction during the skeleton extraction process.A junction is merged with a neighbour if σ′＜0.9σ,where σ′and σ are the centeredness of the merged and original junctions respectively.Finally the skeleton joints are repositioned to better centre them in the mesh.

Please see the original paper for full details.An example of a resulting skeleton is shown in Fig.1(a).

3.2.2 Skeleton transformation

Next we apply the canonical form method of Elad and Kimmel[2]to the skeleton.We use Dijkstra's algorithm to compute the geodesic distances between all the joints of the skeleton,and then use Eq.(1)to perform multidimensional scaling.An example of the result is shown in Fig.1(b).While this still has high time complexity,it now depends on the number of joints in the skeleton instead of the number of mesh vertices.In practice this number is significantly smaller,and therefore computing the canonical form of a skeleton takes significantly less time.

3.2.3 Mesh deformation

Finally we deform the mesh to match the canonical transformation of its skeleton using a method of Yan et al.[30].We use this method as it is simple to implement,fully automatic,does not require any vertex weights to be assigned,and does not have any parameters which require training or manual-tuning. It works by first assigning each triangle to a bone of the original skeleton,and then calculating the transformation of each bone between the original and canonical skeletons.A sparse linear system is then solved,which transforms each triangle according

to the transformation of its assigned bone whilst preserving the mesh's connectivity.

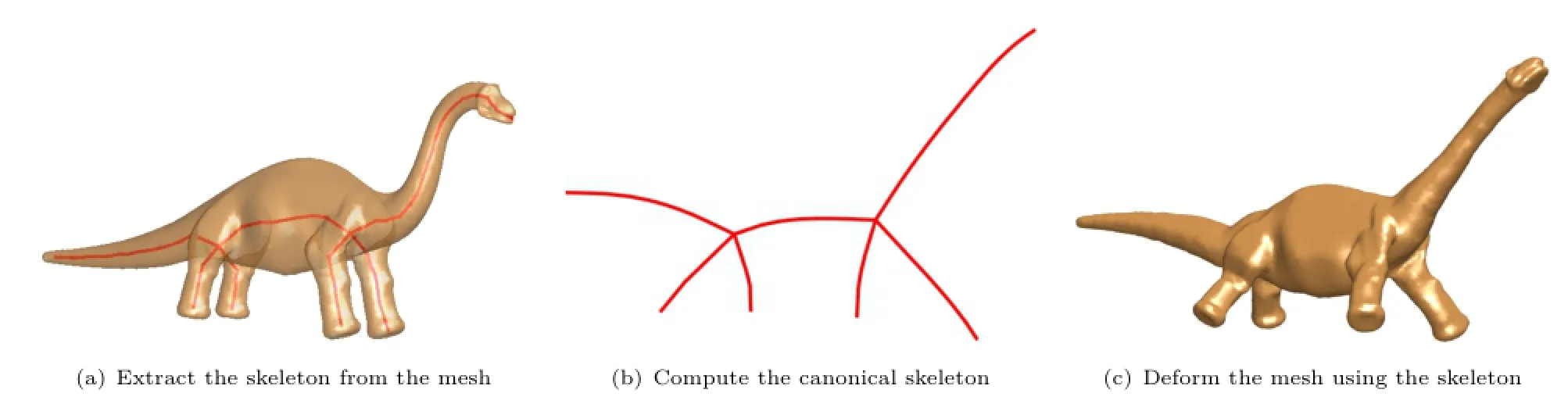
Fig.1 Outline of our method.

Yan et al.'s original method takes into account translation,rotation,and scaling of the skeleton when deforming the mesh,but we ignore scaling and translation as we only care about transforming the articulation of the mesh,and we do not want any stretching of the skeleton caused by the canonicalisation to be transferred to the mesh.We also use our own method for assigning triangles to bones,because the method by Yan et al.requires that the ends of the skeleton protrude outside the mesh,which is not the case for our skeletons;we can retain information from the skeleton extraction procedure to make this assignment.

The skeleton extraction method results in each vertex being assigned to a joint of the skeleton[29]. This assignment is based on which joint each vertex was collapsed to during skeleton extraction.These assignments provide the ones required by Yan et al.'s deformation method.For each joint,we find all the triangles which have at least one vertex assigned to that joint.Each triangle is then assigned to one of the bones connected to that joint.To determine to which of these bones a particular triangle is assigned, we first calculate a plane which bisects each pair of bones that meet at the joint.A triangle is assigned to a particular bone if two or more of its vertices lie on that bone's side of all the bisection planes between it and the other bones.This is illustrated in Fig.2.If a triangle does not meet the assignment criteria for any of the bones,then one of its neighbours is randomly selected and it is given the same bone assignment as that neighbour.See Algorithm 1.

An example of a resulting canonical mesh is shown in Fig.1(c).The mesh has been placed into the canonical pose of the skeleton,but with very little shape distortion,hence preserving the surface details.

4 Experiments

We compare our skeleton canonical forms to several other methods using the two most recently developed publicly available datasets for benchmarking.In Section 4.1,we present our retrieval performance on the SHREC'15 canonical forms benchmark[3]. Secondly,in Section 4.2,we present the results of our experiments on the SHREC'15 non-rigid retrieval benchmark[12].Finally,we consider some limitations of our method in Section 4.3.

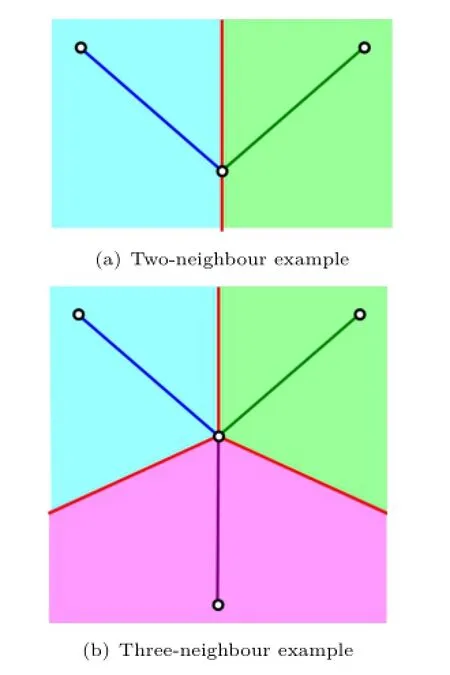
Fig.2 Two dimensional illustration of the assignment regions for bone assignment.The separation planes are shown in red,and the assignment regions are illustrated in the same colour as the corresponding bone.If at least two vertices of a triangle fall within an assignment region,the triangle is assigned to the corresponding bone.

Algorithm 1:Algorithm for assigning triangles to bones Input:mesh,skeleton,assignment of vertices to joints. Output:assignment of each triangle to a bone. for all joints j in skeleton do bisectionPlanes←Ø for all bones b1connected to j do for all bones b2connected to j,where b1/=b2do bisectionPlanes←plane bisecting b1and b2end for end for for all triangles t with a vertex assigned to j do for all bones b connected to j do if ≥ 2 vertices of t fall on b's side of all bisectionPlanes then assign t to b end if end for if t is unassigned then randomly select a neighbouring triangle n of t copy bone assignment of n to t end if end for end for

4.1 SHREC'15 canonical forms benchmark

Our method was recently entered into the SHREC'15 canonical forms benchmark[3].The purpose of this benchmark was to compare the effectiveness of different methods at producing canonical forms for 3D shape retrieval.The dataset used for this benchmark contains 100 meshes,split into 10 different shape classes.Each shape class contains a mesh in 10 different non-rigid poses.The average number of vertices per mesh is 21,141.The dataset contains models from both the SHREC'11 non-rigid benchmark[25],which provides a wide range of shape classes,and the SHREC'14 non-rigid humans benchmark[13],where shape details are important for distinguishing between them.Our method was one out of ten methods which took part. The canonical forms determined by each method were input to a view-based retrieval method[26]to test their effectiveness for non-rigid retrieval.Here we update our results obtained with this benchmark,as we have rewritten some of our code to improve the speed of our implementation and therefore no longer require the largest meshes(with～60,000 vertices) in the dataset to be simplified,as was done for the original benchmark paper.This speed-up is achieved purely through coding changes,with no alterations to the algorithms used.The MDS-based methods tested all use simplified meshes with 2000 vertices as input,as these methods are too computationally expensive to be able to compute canonical forms of the full resolution meshes in a reasonable amount of time.All other methods use full resolution meshes as input.The retrieval results are shown in Table 1. All the performance measures produce a value in the interval[0,1]and are defined as follows:

Nearestneighbour(NN).The fraction of closest matches which are members of the query model's class.

First tier(FT).The fraction of models which are members of the query model's class that appear within the top C closest matches,where C is the number of models in the query's class.

Second tier(ST).The fraction of models which are members of the query model's class that appear within the top 2C closest matches,where C is the number of models in the query's class.

Discounted cumulative gain(DCG).This weights correct matches more if they are higher inthe list of retrieved results.The DCG is computed by first assigning each model Giin the retrieved list G a value of 1 if it is a member of the query's class, and 0 otherwise.An initial DCG is then computed as

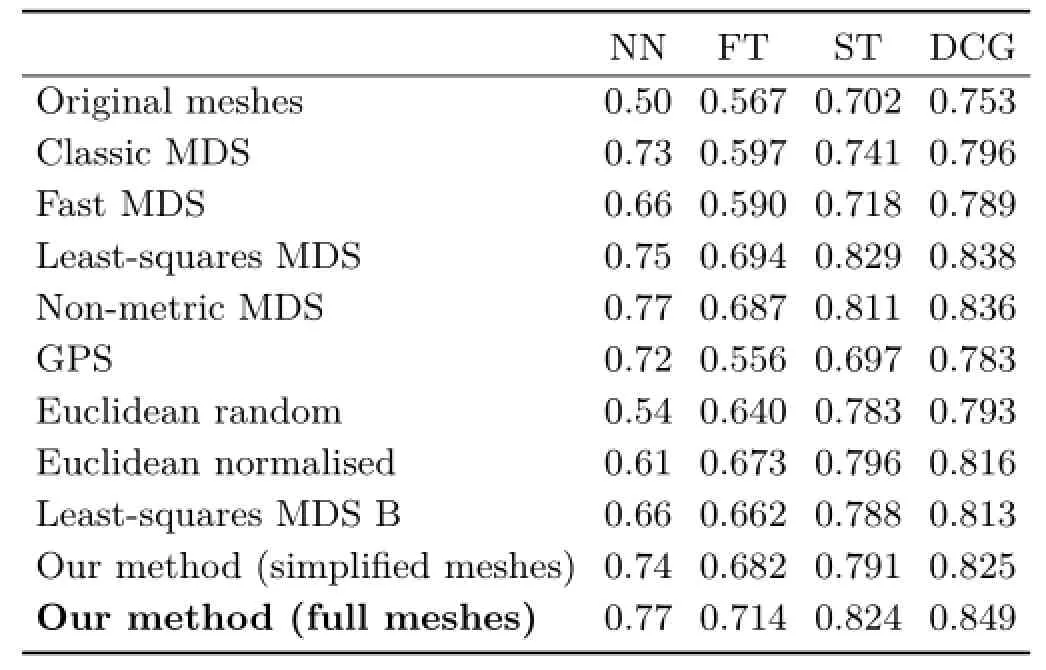
Table 1 Comparison of methods on the SHREC'15 canonical forms benchmark[3]using a view-based retrieval method[26].Original meshes refer to performing retrieval without using canonical forms. Our method achieves the highest retrieval score on three of the four measures

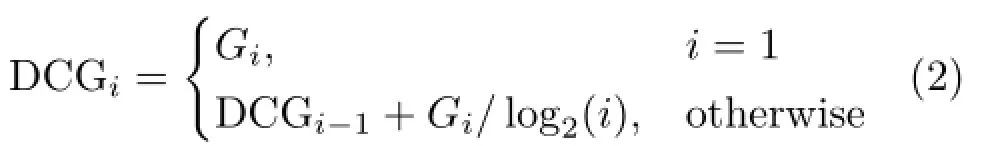
The final result where i=N,N is the number of models in the dataset,is divided by the optimal DCG:

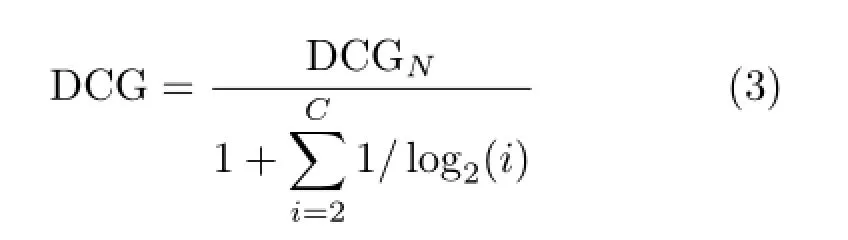
where C is the number of models in the query's class.

The original submission of our method gave a very competitiveperformance,achievingthe third highest retrieval scores behind the leastsquares and non-metric MDS methods based on the mesh's geodesic distances.Our updated result, which uses the full resolution meshes,raises our ranking to achieve state-of-the-art results,with the highest retrieval performance according to three of the four performance measures.This performance increase is likely due to the full resolution meshes containing important details which are lost by mesh simplification.This highlights the importance of being able to efficiently handle meshes with a large number of vertices,and using a canonical form method which preserves local details.We also show the precision–recall curve[31]of each method in Fig.3.Our method achieves the best precision for

low and high recall values,falling below least-squares MDS for mid-range recall values as reflected by the slightly lower second tier measure in Table 1.

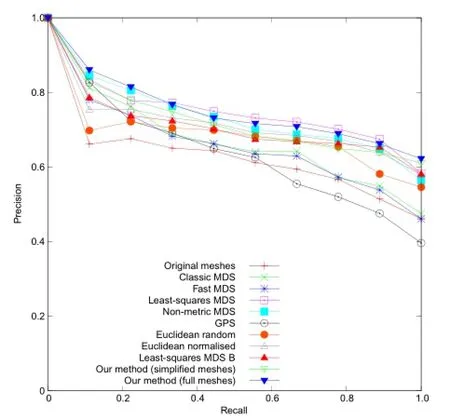
Fig.3 Precision–recall curves for each method tested on the SHREC'15 canonical forms benchmark[3]using a view-based retrieval method[26].Our method achieves the best precision for low and high recall values,falling below least-squares MDS for mid-range recall values.

4.2 SHREC'15 non-rigid shape retrieval benchmark

The SHREC'15 non-rigid benchmark[12]contains a far larger number of 3D models,and therefore we also performed experiments on this dataset.The purpose of this benchmark was to compare stateof-the-art non-rigid shape retrieval methods.This dataset contains 1200 meshes,split into 50 different shape classes. Each shape class contains a mesh within 24 different non-rigid poses.Four meshes in each shape class contain topological errors,such as disconnected components,or unwanted connections (Fig.4).The average number of vertices per mesh is 9607.We compare our canonical forms against those submitted to the SHREC'15 canonical forms benchmark[3],as we have their implementations. We omitted the least-squares MDS B method,as it is simply the same as the least-squares method,but with an early termination from the MDS algorithm which has shown to decrease the quality of the canonical forms[3].

Figure 5 shows two example meshes and their associated canonical forms produced using each method.It is noticeable that the GPS method and the MDS-based methods severely distort local shape details. The Euclidean canonical form methods cause slightly less shape distortion,but sometimes fail to completely stretch out the limbs of the shape.

Our skeleton method achieves a similar pose to the MDS-based methods,but with the least shape distortion of all the methods.

Fig.4 Canonical forms for a mesh with incorrect connections.

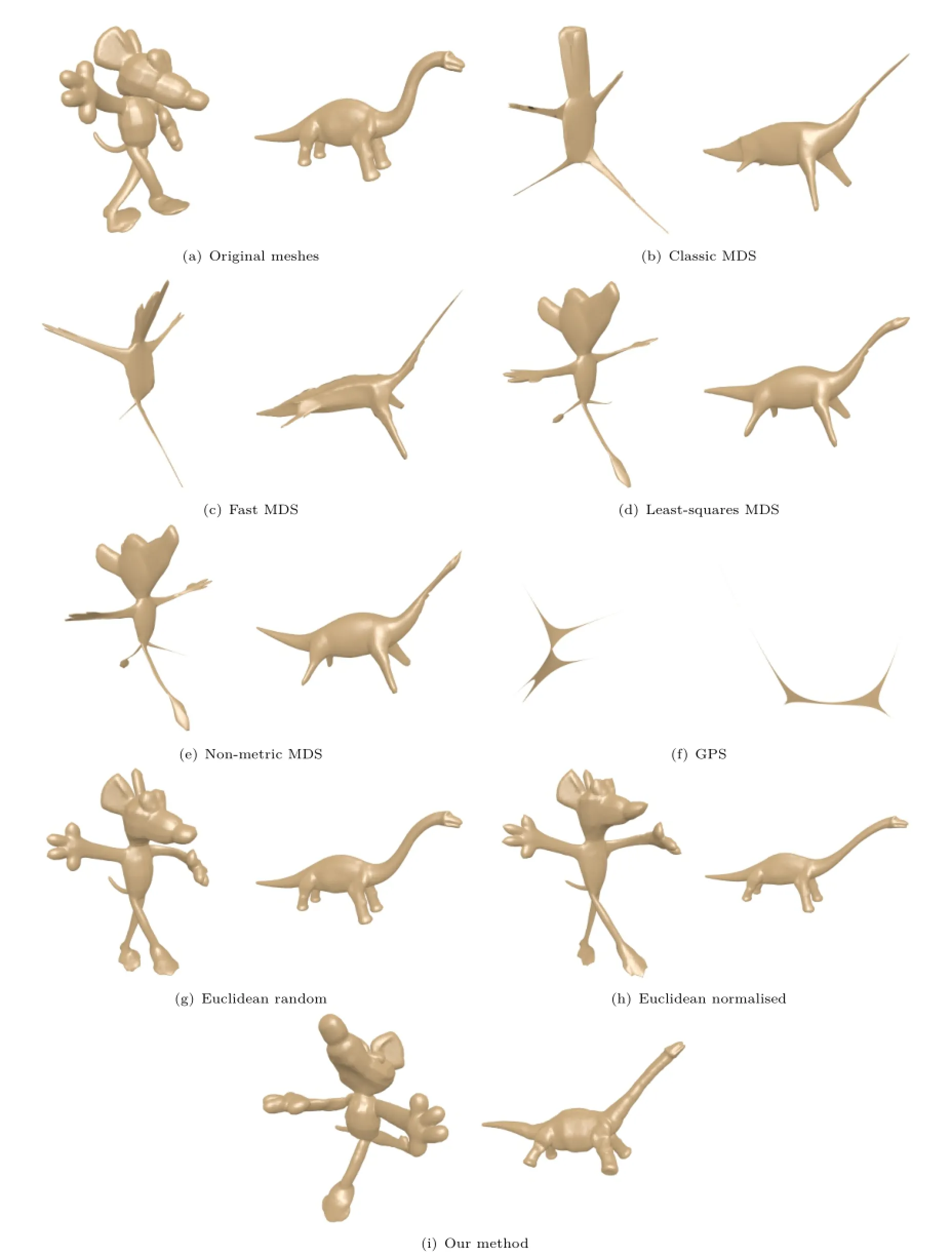
Fig.5 Example canonical forms for each method tested on the SHREC'15 non-rigid dataset[12].

Figure 6 shows the canonical forms for six meshes from the armadillo shape class of the SHREC'15 non-rigid dataset,for each of the methods. Our method produces a consistently similar pose to least-squares MDS,but with less shape distortion.

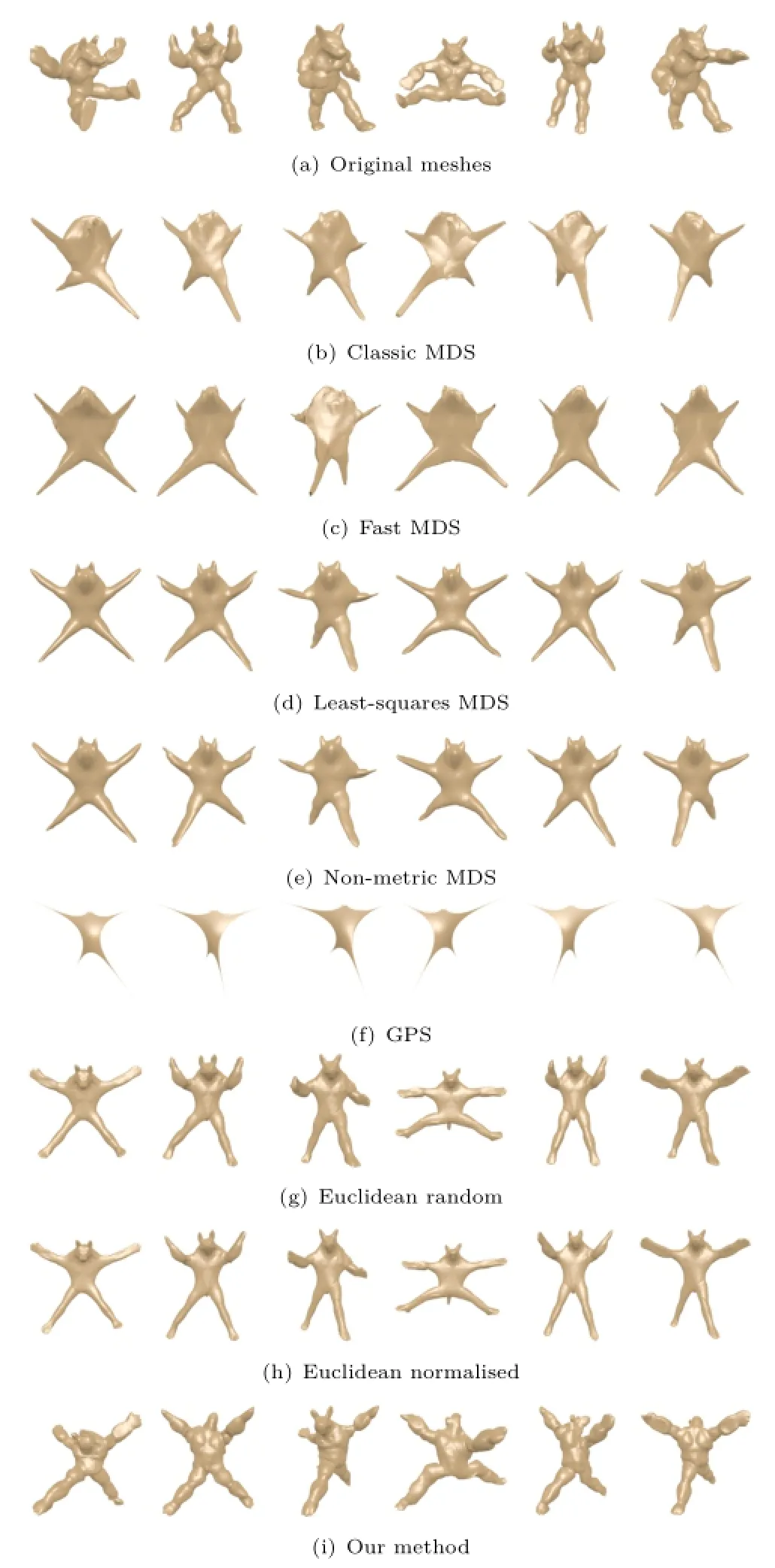
Fig.6 Example of six canonical forms of the same mesh for each method tested on the SHREC'15 non-rigid dataset[12].

Ourmethodhoweverdoesexhibitsomeextra inconsistency with respect to the pose of the head of the armadillo. The classic MDS,Fast MDS, and GPS methods distort the shape so much that it becomes almost unrecognisable.The Euclideanbased methods distort the shape details less than all methods except ours,but do not produce as consistent a canonical pose.

Some of the meshes contained within this dataset have topological errors,to increase the difficulty of the retrieval challenge.In some objects,the mesh is disconnected into two or three different components. The Euclidean distance based methods by Pickup et al.[21]do not require any modification for this, but all the other methods fail on these meshes.For the MDS and GPS methods,we therefore delete all but the largest component. For our skeleton method,we tested two different solutions.The first is to join the separate skeletons for each component by merging the closest joints between components, and the second method is identical to the solution for the MDS and GPS methods.Figure 7 shows an example of this problem,where the mouse's head is disconnected from its body.The methods which only keep the largest component therefore produce canonical forms without the presence of the mouse's head.The Euclidean distance based methods separate out the head and the body,as there are no edge connections keeping them together. Our method which connects the skeletons,places the head in an odd position.This is because,although the skeletons are connected,the method has no mesh connections to preserve between the head and the body.

Allthecanonicalformsfrom each method were input to a view-based retrieval method[26] to test their effectiveness for non-rigid retrieval. The retrieval results are shown in Table 2,and the precision–recall curves are shown in Fig.8. Our method achieves the third highest retrieval performance on this dataset,behind the least-squares and non-metric MDS methods.This may be because the details matter less with this dataset, as the difference between the shape classes is much larger,and therefore keeping the details may only serve to increase the level of noise in the result. Using no canonical forms at all achieved a higher retrieval performance than the classic MDS,fast MDS,and GPS methods,and achieved a higher nearest neighbour performance than the Euclidean distance based methods.Such a high performance from a rigid retrieval method shows that the different shape classes are easily distinguishable even when the non-rigid nature of the shapes is ignored.The precision–recall curves show that there is a noticeable gap in performance between our method,along with the least-squares and non-metric MDS methods,and the others.

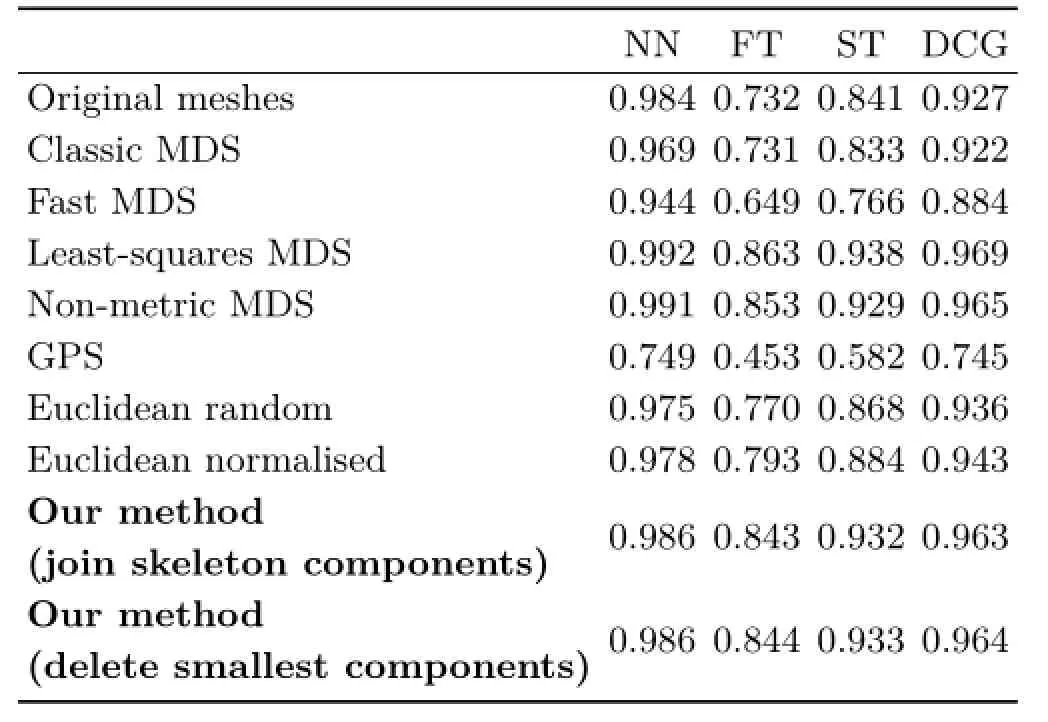
Table 2 Method comparison using SHREC'15 non-rigid benchmark[12]and a view-based retrieval method[26].Original meshes refer to retrieval performance without using canonical forms. Our method achieves the third best retrieval performance,behind two much more computationally expensive methods

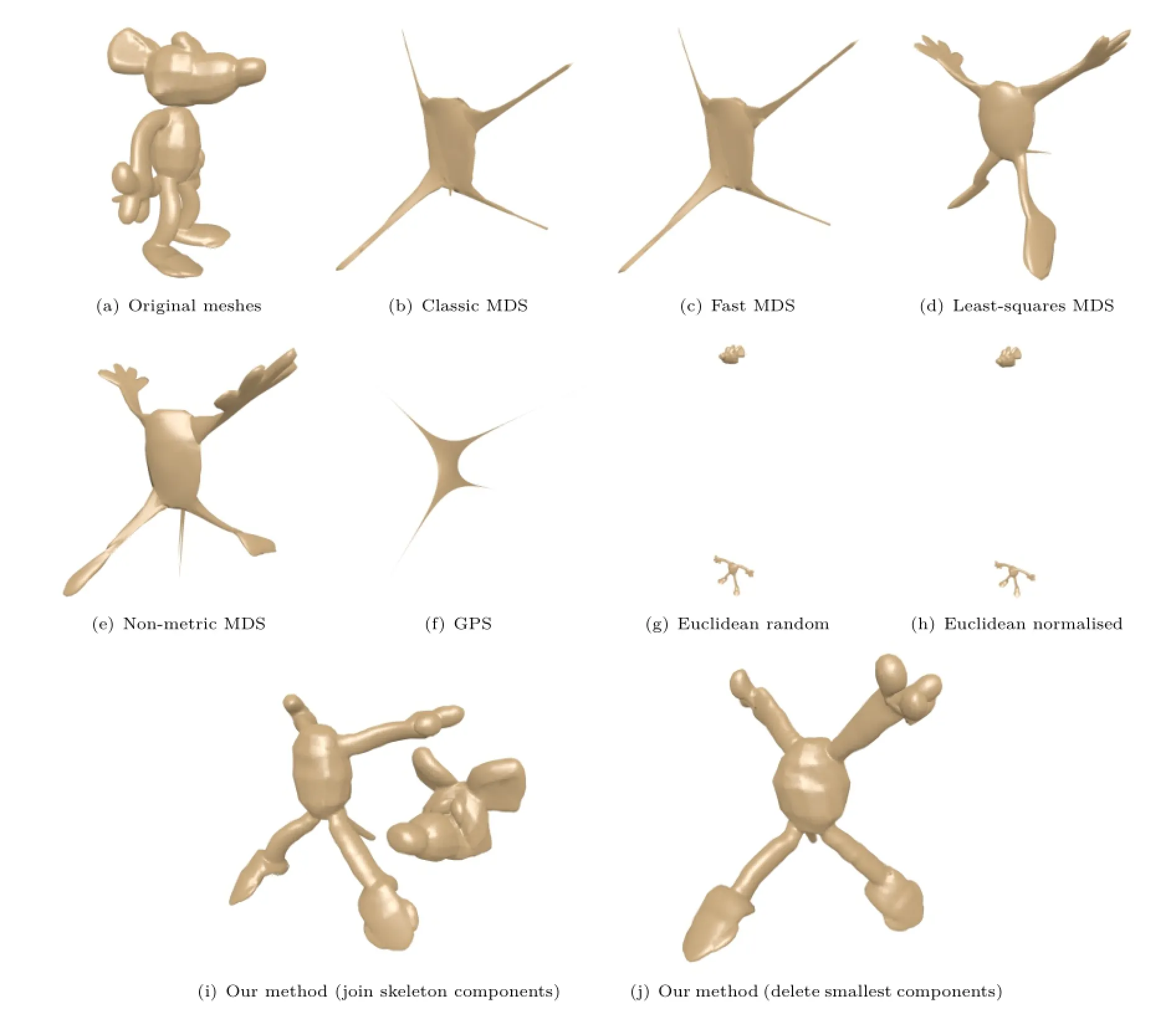
Fig.7 Canonical forms for a mesh with disconnected components.

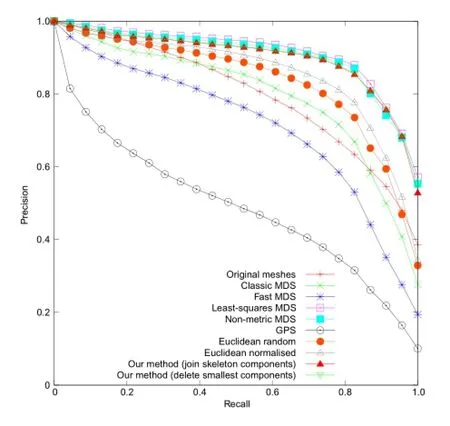
Fig.8 Precision–recall curves for each method tested using the SHREC'15 non-rigid benchmark[12]and a view-based retrieval method[26].Our method achieves the third best performance.

Table 2 shows the performance of both our methods for dealing with disconnected components.

We achieve a tiny performance increase of 0.001 when only keeping the largest mesh component.This probably means that this is a better solution,but as there is only a small proportion of meshes with this problem(15 out of 1200),they only make a minor impact on the overall performance.

Timings for each canonical form method on the non-rigid benchmark are shown in Table 3. The methods were run on a Linux PC with an Intel i7-3930K 3.2 GHz processor and 32 GB of memory.All methods were primarily implemented in Matlab,but with some parts in C++for speed.The times for the four MDS-based methods are for meshes which were simplified to approximately 2000 vertices:it may take in excess of 20 minutes to compute the canonical form for a single full resolution mesh using these methods.Even with much lower resolution meshes,the MDS-based methods are the slowest due to their use of geodesic distances.Our method is the second fastest of all methods,being beaten in run-time by the GPS method.The latter performed worst in all retrieval experiments,however.

In summary,our method is significantly faster than those methods which achieved a slightly better retrieval performance,and achieves a significantly higher retrieval performance than the only method which had a faster run-time.We therefore achieve a very good trade-off between retrieval accuracy and efficiency.

4.3 Limitations

The skeleton refinement step described in Section 3.2.1 does not always merge junctions which are undesirably separate. An example of this is shown in Fig.9,where each of the arms and legs of the alligator are connected to the spine ata different junction.This is likely caused by the curvature of the alligator's spine. This leads to the neck of the alligator not fully straightening out correctly,but even with this local inaccuracy,we still achieve a retrieval nearest neighbour score of 1 for this mesh.There is room for future improvement to the skeleton refinement process,but this is a challenging problem as looser conditions for junction merging can lead to incorrect merging of junctions which should be separate.

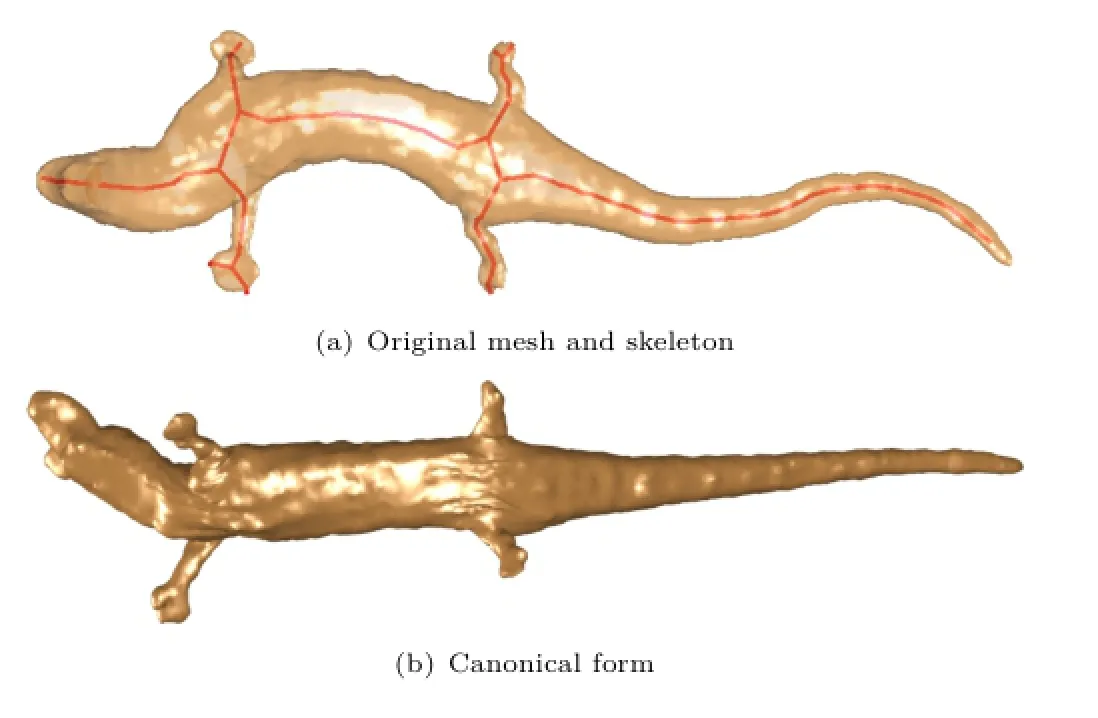
Fig.9 Example of junctions which have not been correctly joined, and the impact on the canonical form.

The SHREC'15 non-rigid benchmark[12]contains some meshes with topological errors. We have already discussed meshes which contain multiple components in Section 4.2,but this dataset also contains meshes where parts of the mesh are undesirably fused. Figure 4 shows an example mesh with this kind of topological error,and the resulting canonical form produced by each method we have tested.It can be seen that the arms of the manikin are incorrectly fused together along the forearms,which means that the arms are not correctly separated by any of the canonical form methods. There are currently no canonical form methods of which we are aware that can correct this kind of topological error.The method by Boscaini et al.[22]proposes a method to handle errors where the incorrect connections are much smaller.

Our method is designed to work on objects which have a natural skeletal structure.Figure 10 shows a mesh from the paper class of the SHREC'15 nonrigid dataset.This mesh does not have a natural skeletal structure,and therefore our method fails to produce a sensible result.Our method would work for other man-made objects,as long as they have an

obvious skeletal structure.

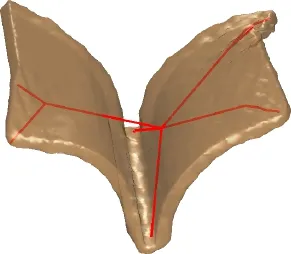
Fig.10 Example of a mesh which does not have a natural skeleton structure.

5 Conclusions

We have presented a novel method for computing the canonical form of a 3D mesh,which uses the mesh's skeleton to normalise its pose.We have shown that our method is able to achieve the same bendinginvariant pose as the previous state-of-the-art,whilst causing far less shape distortion than other methods. Our method is not able to correct for topological errors present in a mesh,and therefore there is room for future research in this direction.The retrieval performance produced using our canonical forms are competitive with other canonical form methods, achieving top performance on a recent canonical forms benchmark.Our method achieves high quality canonical forms,whilst achieving a significantly faster computation time over the previous state-ofthe-art.

Acknowledgements

This work was supported by EPSRC Research Grant No.EP/J02211X/1.

[1]Li,B.;Godil,A.;Aono,M.;Bai,X.;Furuya,T.;Li,L.; L´opez-Sastre,R.;Johan,H.;Ohbuchi,R.;Redondo-Cabrera,C.;Tatsuma,A.;Yanagimachi,T.;Zhang, S.SHREC'12 track:Generic 3D shape retrieval.In: Proceedings of the 5th Eurographics Conference on 3D Object Retrieval,119–126,2012.

[2]Elad,A.;Kimmel,R.On bending invariant signatures for surfaces.IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.25,No.10,1285–1295, 2003.

[3]Pickup,D.;Sun,X.;Rosin,P.L.;Martin,R.R.; Cheng,Z.;Nie,S.;Jin,L.Canonical forms for nonrigid 3D shape retrieval.In:Proceedings of the 2015 Eurographics Workshop on 3D Object Retrieval,99–106,2015.

[4]Chen,D.-Y.;Tian,X.-P.;Shen,Y.-T.;Ouhyoung, M.On visual similarity based 3D model retrieval. Computer Graphics Forum Vol.22,No.3,223–232, 2003.

[5]Johnson,A.E.;Hebert,M.Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.21,No.5,433–449,1999.

[6]Tangelder,J.W.H.;Veltkamp,R.C.A survey of content based 3D shape retrieval methods.Multimedia Tools and Applications Vol.39,No.3,441–471,2008.

[7]Boyer,E.;Bronstein,A.M.;Bronstein,M.M.; Bustos,B.;Darom,T.;Horaud,R.;Hotz,I.;Keller, Y.;Keustermans,J.;Kovnatsky,A.;Litmany,R.; Reininghaus,J.;Sipiran,I.;Smeets,D.;Suetens,P.; Vandermeulen,D.;Zaharescu,A.;Zobel,V.SHREC 2011: Robustfeature detection and description benchmark.In:Proceedings of the 4th Eurographics Conference on 3D Object Retrieval,71–78,2011.

[8]Smeets,D.;Keustermans,J.;Vandermeulen,D.; Suetens,P.meshSIFT:Local surface features for 3D face recognition under expression variations and partialdata.ComputerVision and Image Understanding Vol.117,No.2,158–169,2013.

[9]Ben-Chen,M.;Gotsman,C.Characterizing shape using conformal factors.In:Proceedings of the 1st Eurographics Conference on 3D Object Retrieval,1–8, 2008.

[10]Giachetti,A.;Lovato,C.Radial symmetry detection and shape characterization with the multiscale area projection transform.Computer Graphics Forum Vol. 31,No.5,1669–1678,2012.

[11]Sun,J.;Ovsjanikov,M.;Guibas,L.A concise and provably informative multi-scale signature based on heat diffusion.Computer Graphics Forum Vol.28,No. 5,1383–1392,2009.

[12]Lian,Z.;Zhang,J.;Choi,S.;ElNaghy,H.;El-Sana, J.;Furuya,T.;Giachetti,A.;Guler,R.A.;Lai,L.;Li, C.;Li,H.;Limberger,F.A.;Martin,R.;Nakanishi,R. U.;Neto,A.P.;Nonato,L.G.;Ohbuchi,R.;Pevzner, K.;Pickup,D.;Rosin,P.;Sharf,A.;Sun,L.;Sun,X.; Tari,S.;Unal,G.;Wilson,R.C.Non-rigid 3D shape retrieval.In:Proceedings of the 2015 Eurographics Workshop on 3D Object Retrieval,107–120,2015.

[13]Pickup,D.;Sun,X.;Rosin,P.L.;Martin,R.R.; Cheng,Z.;Lian,Z.;Aono,M.;Hamza,A.B.; Bronstein,A.;Bronstein,M.;Bu,S.;Castellani,U.; Cheng,S.;Garro,V.;Giachetti,A.;Godil,A.;Han, J.;Johan,H.;Lai,L.;Li,B.;Li,C.;Li,H.;Litman, R.;Liu,X.;Liu,Z.;Lu,Y.;Tatsuma,A.;Ye,J. Shape retrieval of non-rigid 3D human models.In:

Proceedings of the 7th Eurographics Workshop on 3D Object Retrieval,101–110,2014.

[14]Hilaga,M.;Shinagawa,Y.;Kohmura,T.;Kunii,T. L.Topology matching for fully automatic similarity estimation of 3D shapes.In: Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques,203–212,2001.

[15]Sfikas,K.;Theoharis,T.;Pratikakis,I.Non-rigid 3D object retrieval using topological information guided by conformal factors.The Visual Computer Vol.28, No.9,943–955,2012.

[16]Reuter,M.;Wolter,F.-E.;Peinecke,N.Laplace–Beltrami spectra as‘Shape-DNA'of surfaces and solids.Computer-Aided Design Vol.38,No.4,342–366,2006.

[17]Smeets, D.; Hermans, J.; Vandermeulen,D.; Suetens,P.Isometric deformation invariant 3D shape recognition.Pattern Recognition Vol.45,No.7,2817–2831,2012.

[18]Shamai,G.;Zibulevsky,M.;Kimmel,R.Accelerating the computation of canonical forms for 3D nonrigid objects using multidimensionalscaling. In:Proceedings of the 2015 Eurographics Workshop on 3D Object Retrieval,71–78,2015.

[19]Lian,Z.;Godil,A.;Xiao,J.Feature-preserved 3D canonical form.International Journal of Computer Vision Vol.102,No.1,221–238,2013.

[20]Wang,X.-L.;Zha,H.Contour canonical form:An efficient intrinsic embedding approach to matching non-rigid 3D objects.In:Proceedings of the 2nd ACM International Conference on Multimedia Retrieval, Article No.31,2012.

[21]Pickup,D.;Sun,X.;Rosin,P.L.;Martin,R.R. Euclidean-distance-based canonical forms for non-rigid 3D shape retrieval.Pattern Recognition Vol.48,No.8, 2500–2512,2015.

[22]Boscaini, D.; Girdziuˇsas, R.; Bronstein, M. M.Coulomb shapes: Using electrostatic forces for deformation-invariant shape representation.In: Proceedings of the 7th Eurographics Workshop on 3D Object Retrieval,9–15,2014.

[23]Crane,K.;Weischedel,C.;Wardetzky,M.Geodesics in heat:A new approach to computing distance based on heat flow.ACM Transactions on Graphics Vol.32, No.5,Article No.152,2013.

[24]Ying,X.;Xin,S.-Q.;He,Y.Parallel chen-han(PCH) algorithm for discrete geodesics.ACM Transactions on Graphics Vol.33,No.1,Article No.9,2014.

[25]Lian,Z.;Godil,A.;Bustos,B.;Daoudi,M.;Hermans, J.;Kawamura,S.;Kurita,Y.;Lavou´e,G.;Nguyen, H.V.;Ohbuchi,R.;Ohkita,Y.;Ohishi,Y.;Porikli, F.;Reuter,M.;Sipiran,I.;Smeets,D.;Suetens, P.;Tabia,H.;Vandermeulen,D.SHREC'11 track: Shape retrieval on non-rigid 3D watertight meshes.In: Proceedings of the 4th Eurographics Conference on 3D Object Retrieval,79–88,2011.

[26]Lian,Z.;Godil,A.;Sun,X.;Xiao,J.CM-BOF:Visual similarity-based 3D shape retrievalusing clock matching and bag-of-features.Machine Vision and Applications Vol.24,No.8,1685–1704,2013.

[27]Kimmel,R.;Sethian,J.A.Computing geodesic paths on manifolds.Proceedings of the National Academy of Sciences of the United States of the America Vol.95, No.15,8431–8435,1998.

[28]Borg,I.;Groenen,P.J.F.Modern Multidimensional Scaling: Theory and Applications.Springer-Verlag New York,2005.

[29]Au,O.K.-C.;Tai,C.-L.;Chu,H.-K.;Cohen-Or,D.; Lee,T.-Y.Skeleton extraction by mesh contraction.In: Proceedings of ACM SIGGRAPH 2008 Papers,Article No.44,2008.

[30]Yan,H.-B.;Hu,S.-M.;Martin,R.;Yang,Y.-L. Shape deformation using a skeleton to drive simplex transformations.IEEE Transactions on Visualization and Computer Graphics Vol.14,No.3,693–706,2008.

[31]Baeza-Yates,R.A.;Ribeiro-Neto,B.A.Modern Information Retrieval:The Concepts and Technology behind Search,2nd edn.Harlow,England:Pearson Education Ltd.,2011.

David Pickup obtained his M.Eng. degree from the University of Bristol and Ph.D.degree from the University ofBath.He is currently a postdoctoral research associate in the Visual Computing research group, Cardiff University.His current research centres on three-dimensional shape retrieval.

Xianfang Sun received his Ph.D.from the Institute of Automation,Chinese Academy of Sciences,in 1994.He is currently a senior lecturer in the School of Computer Science& Informatics, Cardiff University,Wales,UK.His main research interests include computer vision, computer graphics, pattern recognition,and artificial intelligence.

PaulL.Rosin isa professorin the School of Computer Science & Informatics, Cardiff University. Previous posts include lecturer in the DepartmentofInformation Systems and Computing at Brunel University London, UK,research scientist in the Institute for Remote Sensing ApplicationsatJointResearch Centre,Ispra,Italy, and lecturer at Curtin University of Technology,Perth, Australia.His research interests include the representation, segmentation,and grouping of curves,knowledge-based

vision systems,early image representations,low level image processing,machine vision approaches to remote sensing, methods for evaluation of approximation algorithms,etc., medical and biological image analysis,mesh processing, non-photorealistic rendering,and the analysis of shape in art and architecture.

Ralph R. Martin obtained his Ph.D.degree in 1983 from Cambridge University.Sincethen hehasbeen at Cardiff University,where he now holds a Chair and leads the Visual Computing research group.He is also a guestprofessoratTsinghua and two other universities in China,and is a director of Scientific Programmes of the One Wales Research Institute of Visual Computing.His publications include about 300 papers and 15 books covering such topics as solid modelling,surface modelling,reverse engineering, intelligent sketch input,mesh processing,video processing, computer graphics,vision based geometric inspection, and geometric reasoning.He is a Fellow of the Learned Society of Wales,the Institute of Mathematics and its Applications,and theBritish ComputerSociety.He is on the editorial boards of Computer-Aided Design, Computer Aided Geometric Design,Geometric Models,and Computational Visual Media.

Open Access The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License(http:// creativecommons.org/licenses/by/4.0/), which permits unrestricted use,distribution,and reproduction in any medium,provided you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons license,and indicate if changes were made.

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript,please go to https://www. editorialmanager.com/cvmj.

1School of Computer Science and Informatics, CardiffUniversity,Cardiff, CF24 3AA,UK.E-mail: D.Pickup,PickupD@Cardiff.ac.uk(); X. Sun,SunX2@Cardiff.ac.uk;P.L.Rosin,RosinPL@ Cardiff.ac.uk;R.R.Martin,MartinRR@Cardiff.ac.uk.

Manuscript received:2016-01-26;accepted:2016-02-20