电磁波在不均匀尘埃等离子体中的衰减特性

李海英 孔鹏飞 詹捷 吴振森 白璐

(1.西安电子科技大学物理与光电工程学院,西安 710071;2.西安电子科技大学信息感知技术协同创新中心,西安 710071)



电磁波在不均匀尘埃等离子体中的衰减特性

李海英1,2孔鹏飞1詹捷1吴振森1,2白璐1,2

(1.西安电子科技大学物理与光电工程学院,西安 710071;2.西安电子科技大学信息感知技术协同创新中心,西安 710071)

基于WKB近似方法,研究了高频电磁波入射不均匀尘埃等离子体中的衰减特性.对弱电离尘埃等离子体复相对介电常数的分布特征进行了分析,讨论了电子数密度、尘埃颗粒数密度对复相对介电常数虚部的影响.利用电子密度分布的抛物模型,数值计算了电磁波以不同角度入射不均匀尘埃等离子体的衰减特性,对入射角、电子数密度、尘埃颗粒半径和尘埃颗粒数密度对衰减系数的影响进行了分析.结果表明:随着电子数密度、尘埃颗粒数密度和半径增大,衰减系数也会变大.

尘埃等离子体;WKB近似方法;衰减

DOI 10.13443/j.cjors.2015111301

引 言

尘埃等离子体是参杂有尘埃颗粒的电离气体,也被称为复杂等离子体,广泛存在于星际云、行星环和行星磁层等空间环境以及半导体科学、材料科学领域中.尘埃颗粒影响地球近地空间的电磁环境,会对空间通信系统产生不可预估的影响;而实验室中尘埃颗粒则会造成等离子体刻蚀半导体芯片过程中污染.尘埃颗粒的存在使得尘埃等离子体具有许多不同于传统等离子体的特点[1-2].自二十世纪八十年代开始,尘埃等离子体物理科学便吸引了大量学者的关注,成为等离子体物理的一个新的重要分支.

目前,高频电磁波与尘埃等离子体的相互作用已经成为众多学者的研究兴趣之一.等离子体中的尘埃颗粒会通过与电子、离子发生碰撞,充电和电磁力等作用改变传统等离子体的物理性质,例如:使体系具有异常的电磁特性.国内外许多学者和专家从不同角度研究了尘埃等离子体的特性[3-6]以及尘埃等离子体与极区中层夏季雷达回波(Polar Mesosphere Summer Echoes,PMSE)的产生机制之间的联系.中科院电子所李芳研究员研究了等离子体中尘埃粒子的电磁波吸收效应[3],以及电磁波被尘埃等离子体散射的功率谱等问题[4].挪威特罗瑟姆大学的Havnes教授等人对有关带电尘埃粒子与PMSE现象之间的关系进行了充分的研究[7-8].Scales研究了地球中层大气中的带电尘埃云的电动结构[9].石雁祥等人讨论了充电对尘埃等离子体的介电常数和电导率的影响[6],估算了两种弱电离层尘埃等离子体的特征参量[10],给出了弱电离尘埃等离子体的介电张量表达式[11].王菊基于尘埃等离子体角度分析了微波在火箭喷焰中的衰减特性[12].

考虑到中层大气和固体火箭喷焰等环境中的尘埃等离子体实际都为不均匀分布,而在电磁波传播过程中介质不均匀性是重要的影响因素之一,本文基于WKB近似方法对电磁波在不均匀尘埃等离子体中的衰减特性进行了研究,重点分析了电子密度、尘埃颗粒密度和半径对复相对介电常数以及衰减系数的影响.

1 基本理论

1.1 尘埃等离子体的复相对介电常数

尘埃等离子体由尘埃颗粒、电子、离子和中性分子组成,其中电子和离子对尘埃颗粒的充放电会改变体系的总电流,从而影响体系的电导率和介电常数.石雁祥等人基于Boltzman方程和Shukla方程导出了考虑碰撞和充放电影响的尘埃等离子体相对复介电常数[11],具体表示为

(1)

(2)

(3)

式中： Te表示电子温度； a是中性分子半径； Ti表示离子温度.

电荷弛豫速率[2]为

(4)

式中： rd是尘埃粒子半径； KB是波尔兹曼常数； e是电子电荷数； me是电子质量.

1.2 WKB近似方法

WKB近似方法被广泛应用于研究电磁波在等离子体环境中的传播特性.尘埃等离子体具有与传统等离子体相似的性质,因此我们使用WKB近似方法研究电磁波在不均匀尘埃等离子体层中的衰减特性.

由非均匀介质中的麦克斯韦方程组出发,得到非均匀介质中波动方程的WKB解[14]为:

(5)

式中： E0是电场振幅值； k0是空气中的波数; sin θn是第n层介质的入射角正弦值.

进一步可以得到电磁波入射非均匀介质的单程衰减系数[14]为:

(6)

2 数值计算分析

2.1 尘埃等离子体中不同参数对复相对介电常数的影响

研究电磁波在尘埃等离子体中的衰减特性与复相对介电常数的虚部密切相关.本节我们分别讨论了电子数密度,尘埃颗粒数密度对复相对介电常数虚部的影响.图1给出了改变电子数密度,复相对介电常数虚部随入射波频率f的变化.其中中性分子数密度Nm=5×1014cm-3,尘埃颗粒数密度Nd=1×103cm-3,电子和离子温度均设为150 K,尘埃颗粒半径rd=50 nm．

由图1可知:随入射波频率增大,虚部逐渐减小;对同一入射波频率,电子数密度变大,复相对介电常数虚部也增大.

图2给出了尘埃颗粒数密度改变时,尘埃等离子体复相对介电常数的虚部随入射波频率f的变化.其中中性分子数密度Nm=5×1014cm-3,电子数密度Ne=5×105cm-3,电子和离子温度均设为150 K,尘埃颗粒半径rd=100 nm.

由图2可知：频率小于200 MHz时，尘埃颗粒对复相对介电常数虚部有明显影响，频率大于200 MHz时，随频率增大，复相对介电常数虚部逐渐趋于0，尘埃颗粒影响不明显；尘埃颗粒使复相对介电常数虚部增大，但增加量小。

图1 电子数密度改变时,复相对介电常数虚部随入射波频率分布

图2 尘埃颗粒数密度改变时,复相对介电常数虚部随入射波频率分布

2.2 电磁波在不均匀尘埃等离子体中的衰减系数分析

利用WKB近似方法和2.1节给出的尘埃等离子体复相对介电常数,本节对高频电磁波以不同入射方式进入不均匀尘埃等离子体层中的衰减系数进行数值分析,其中设置尘埃等离子体层厚度为15 km,中性分子数密度Nm=5×1014cm-3,电子和离子温度均设为150 K.图3中假定尘埃颗粒半径rd=50 nm,电子数密度满足抛物型分布Ne=N0×[1-(h-h0)2Δh2] cm3,数值计算尘埃等离子体中电子数密度改变时,电磁波垂直入射不均匀尘埃等离子体中的衰减系数随入射波频率f的变化.

由图3可知,衰减系数随入射波频率增大而逐渐减小;电子数密度对衰减系数影响十分显著,当电子数密度增加时,衰减系数也变大.

图4给出了改变电磁波入射角时,衰减系数随入射角的变化.其中抛物型电子数密度表达式中N0=5×105cm-3,尘埃颗粒半径rd=50 nm.对同一个入射频率,当垂直入射尘埃等离子体层时,衰减最小;随入射角增大,衰减系数也不断增大.

图3 电子数密度改变时,衰减系数随入射波频率的变化

图4 入射角改变时,衰减系数随入射波频率的变化

图5(a)和(b)分别计算了尘埃颗粒数密度,颗粒半径对衰减系数的影响.其中电子数密度Ne=5×105cm-3,入射角θi=30°.

由图5可知:尘埃颗粒的存在增大了衰减系数的值;尘埃颗粒数密度相同时,颗粒半径rd=100 nm的衰减系数比rd=50 nm的情况大;尘埃颗粒半径较小时,对衰减系数的影响非常小.

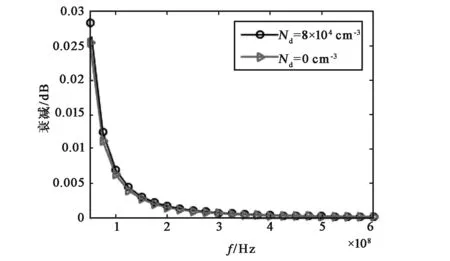
(a) rd=50 nm

(b) rd=100 nm图5 尘埃颗粒数密度、半径改变时,衰减系数随入射波频率的变化

3 结 论

本文基于WKB近似方法数值分析了高频电磁波入射不均匀尘埃等离子体层时,衰减系数随入射波频率的变化.结果表明:电子密度对衰减的影响占优,尘埃颗粒的半径和数密度在一定频段范围内会对衰减系数有明显影响.文中选取的尘埃等离子体中相关参数与大气中层环境比较一致,入射波频率范围包含了目前空间探测中常用的极高频(Very High Frequency,VHF)雷达频段,因此,本文结果对进一步分析研究大气中层对电磁波的传播影响具有一定的理论意义.

[1] 马锦秀. 尘埃等离子体[J]. 物理, 2006, 35(3): 244-250.

MA J X. Dusty plasmas[J]. Physics, 2006, 35(3): 244-250. (in Chinese)

[2] SHUKLA P K, MAMUN A A. Introduction to dusty plasma physics[M]. Florida: CRC Press, 2001.

[3] 李芳, 李廉林, 隋强. 等离子体中尘埃粒子对电磁波的吸收效应[J]. 中国科学E辑, 2004, 34(7): 832-840.

LI F, LI L L, SUI Q. Absorbing effect of dusty particle on electromagnetic wave in plasma[J]. Science in China series E, 2004, 34(7): 832-840. (in Chinese)

[4] 李芳, HAVNES O. 电磁波被尘埃等离子体散射的功率谱[J]. 电子科学学刊, 1999, 21(5): 679-685.

LI Fang, HAVNES O. Scatter spectrum of Radio wave by a Dusty plasma[J]. Journal of Electronics, 1999, 21(5): 679-685. (in Chinese)

[5] GUERRA R, MENDONCA J T. Mie and Debye scattering in dusty plasma[J]. Physical Review E, 2000, 62(1): 1190-1201.

[6] 石雁祥, 葛德彪, 吴健. 尘埃粒子充放电过程对尘埃等离子体电导率的影响[J]. 物理学报, 2006, 55(10): 5318-5324.

SHI Y X, GE D B, WU J. Influence of charge and discharge processed of dust particles on the dust plasma conductivity[J]. Acta physica sinica, 2006, 55(10): 5318-5324. (in Chinese)

[7] HAVNES O, MELANDSØF, HOZ C L, et al. Charged dust in the Earth’s mesopause: Effects on radar backscatter[J]. Physica scripta, 1992, 45: 535-544.

[8] HAVNES O, ASLAKSEN T and BRATTLI A. Charged dust in the earth’s middle atmosphere[J]. Physica scripta, 2001, T89: 133-137.

[9] SCALES W A, GANGULI G. Electrodynamic structure of charged dust clouds in the earth's middle atmosphere[J]. New journal of physics, 2004, 6(1): 12.

[10] 石雁祥, 王菊, 吴健, 等. 对两种弱电离尘埃等离子体特征参量的定量估计[J]. 电波科学学报, 2008, 23(1): 95-100.

SHI Y X, WANG J, WU J, et al. Characteristic parameters estimation of two weakly ionized dusty plasma[J]. Chinese journal of radio science, 2008, 23(1): 95-100. (in Chinese)

[11] 石雁祥, 吴健, 葛德彪. 弱电离尘埃等离子体的介电张量研究[J]. 物理学报, 2009, 58(8): 5507-5512.

SHI Y X, WU J, GE D B. The research on the dielectric tensor of weakly ionized dust plasma[J]. Acta physica sinica, 2009, 58(8): 5507-5512. (in Chinese)

[12] 王菊. 火箭喷焰对微波信号衰减的研究[D]. 西安: 西安电子科技大学, 2006.

WANG J. Study of microwave attenuation in the rocket exhaust[D]. Xi’an: Xidian University, 2006. (in Chinese)

[13] 金兹堡. 电磁波在等离子体中的传播[M]. 北京: 科学出版社, 1978: 66-69.

[14] 庄钊文, 袁乃昌, 刘少斌, 等. 等离子体隐身技术[M]. 北京: 科学出版社, 2006: 67-75.

李海英 (1982-),女,山东人,西安电子科技大学副教授,博士,主要从事随机介质中的电磁波传播及电离层加热实验和理论研究.

孔鹏飞 (1992-),男,江苏人,西安电子科技大学硕士研究生,主要研究方向为电离层加热实验和理论研究.

詹捷 (1990-),女,四川人,西安电子科技大学硕士研究生,主要研究方向为ELF/VLF波传播特性研究.

Attenuation characteristics of electromagnetic waves in nonuniform dust plasma

LI Haiying1,2KONG Pengfei1ZHAN Jie1WU Zhensen1,2BAI Lu1,2

(1.SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710071,China; 2.CollaborativeInnovationCenterofInformationSensingandUnderstandatXidianUniversity,Xi’an710071,China)

Based on Wenzel, Kramers, Brillouin(WKB) approximation method, the attenuation characteristics of high-frequency electromagnetic waves in nonuniform dust plasma are studied. Numerical results of complex relative dielectric constant of weakly ionized dust plasma are presented, and the effects of electron number density, dust number density on imaginary part are given. With parabolic model of electron number density distribution, attenuation characteristics of electromagnetic waves with different incident angles are analyzed, and the effects of incident angles, electron number density, and radius and number density of dust plasma are discussed. The result shows that attenuation factors are increasing with electron number density, radius and number density of dust plasma.

dust plasma; WKB approximation method; attenuation

10.13443/j.cjors.2015111301

2015-11-13

O451

A

1005-0388(2016)04-0654-05

李海英, 孔鹏飞, 詹捷, 等. 电磁波在不均匀尘埃等离子体中的衰减特性[J]. 电波科学学报,2016,31(4):654-658.

LI H Y, KONG P F, ZHAN J, et al. Attenuation characteristics of electromagnetic waves in nonuniform dust plasma[J]. Chinese journal of radio science,2016,31(4):654-658. (in Chinese). DOI: 10.13443/j.cjors.2015111301

联系人： 李海英 E-mail：lihy@xidian.edu.cn