基于并行双尺度射线追踪的海面电磁散射计算

孟肖 郭立新 黄青青 李娟

(西安电子科技大学物理与光电工程学院,西安 710071)



基于并行双尺度射线追踪的海面电磁散射计算

孟肖 郭立新 黄青青 李娟

(西安电子科技大学物理与光电工程学院,西安 710071)

利用一种基于双尺度模型(Two Scale Model,TSM)的射线追踪(Ray Tracing,RT)算法(TSM-RT)快速计算电大尺寸海面电磁散射,与传统的射线追踪算法相比,该算法能够有效减少射线与面元的求交次数,提高了计算效率. 同时,为了进一步减少计算时间,利用图形处理单元(Graphics Processing Unit,GPU)强大的并行处理能力对TSM-RT算法进行加速. 计算结果表明:基于GPU的并行TSM-RT算法与基于CPU的串行TSM-RT算法相比计算时间有了很大程度的减少,获得了很好的加速效果.

双尺度射线追踪(TSM-RT);GPU;并行加速

DOI 10.13443/j.cjors.2015072502

引 言

海面散射的研究在民用以及军事等领域均有广泛用途.我国是一个发展中的海洋大国,拥有18 000多千米的大陆海岸线、14 000多千米的岛屿线和300多万平方千米的海洋国土面积[1]. 海洋对我国经济、军事、科技和生活具有重要影响.

计算粗糙海面散射的方法有很多,其中主要分为数值精确方法和高频近似方法. 对于数值精确方法,常用的有矩量法[2]、有限元方法[3]等,但是由于计算复杂度很高以及对计算机内存的要求,这些数值精确方法往往难以处理电大尺寸散射问题. 因此,高频近似方法近年来在处理电大尺寸散射问题方面发挥到了重要作用. 常见的高频算法主要有几何光学(Geophysical Optics,GO)法和物理光学(Physical Optics,PO)法,其中,PO法由于没有考虑到多次散射问题,所以计算精度不高.另外,射线追踪(Ray Tracing,RT)算法也是一种很常见的高频近似算法,它将GO和PO[4-5]结合起来,其中射线的传播路径由GO来确定,而远区散射场由PO计算.

虽然,与传统的数值算法相比,RT算法的计算速度已经有了很大提高,但是当处理电大问题的时候,仍然需要花费很长时间进行射线追踪. 因此,在传统RT的基础上本文介绍了一种近似RT算法,即基于双尺度模型(Two Scale Model,TSM)的射线追踪(Ray Tracing,RT)算法(TSM-RT).对于TSM-RT计算电大尺寸海面电磁散射,首先将海面按照双尺度模型进行建模,即将海面划分为一系列大三角面元,并且每个大三角面元由许多小三角面元组成.射线路径由大三角面元近似确定,而远区散射场则是所有小三角面元的散射场之和.与传统的RT相比,该方法在保证精度的前提下能够有效减少射线与面元的求交次数,进而提高计算效率.

近年来,并行计算已经得到了广泛应用,尤其是随着图形处理单元(Graphics Processing Unit, GPU)性能的不断提升,许多研究已经转向了拥有高度并行性和可编程的GPU平台上,如数值计算[6-7]、流体模拟[7]、数据库操作[8]等通用计算领域.另外,NVlDlA公司率先提出了统一的计算设备体系结构(Compute Unified Device Architecture, CUDA)[9],CUDA是用于GPU计算的开发环境,它是一个全新的软硬件架构,可以将GPU视为一个并行数据计算的设备,对所进行的计算进行分配和管理.对于TSM-RT算法,每条射线的追踪过程都是相互独立进行的,非常适合利用GPU进行并行加速.因此,为了进一步减少计算时间,本文提出了基于GPU的并行TSM-RT算法,利用GPU强大的并行处理能力对TSM-RT算法进行加速,与基于CPU的串行的TSM-RT相比基于GPU的TSM-RT算法的计算时间有了很大程度的减少,获得了很好的加速效果.

1 基于GPU的TSM-RT算法

对于TSM-RT算法,首先利用蒙特卡洛方法对海面进行建模,如图1所示,然后将海面划分为双尺度模型,也就是将海面划分为一系列大三角面元,并且每个大三角面元由许多小三角面元组成,为了保证计算精度取小三角面元的采样间隔为0.1λ.

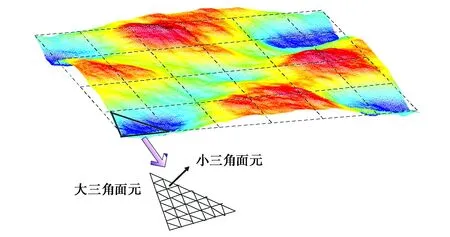
图1 海面双尺度模型

将海面划分为双尺度模型后,射线路径根据GO,由大三角面元近似确定,当射线路径确定后,反射场根据GO计算,由于大三角面元由许多小三角面元组成,具有一定的粗糙度,因此大三角面元上的反射场可以表示为[10]:

Er(r)=R·Ei(r),

(1)

(2)

式中: R0是平面反射系数; kn是入射场矢量在面元外法向量上的投影; δ是粗糙面的均方根高度.

最后,利用PO计算远区散射场,Stratton-Chu积分方程可以表示为

(3)

一个大三角面元上的远区散射场则是它上面所有小三角面元的散射场之和,即

(4)

近年来,随着GPU性能的不断提升,许多的研究已经转向了基于GPU平台上的实现. CUDA是NVIDIA推出的一种CPU+GPU异构运算平台. 在该架构中,GPU可视为一个计算设备,用于处理高度并行的计算. CUDA架构采用了一种全新的计算体系结构来使用GPU提供的硬件资源,图2是CUDA存储模型示意图.

图2 CUDA存储模型

由图2可以看出,每一个线程都拥有自己的私有存储器、寄存器和局部存储器;每一个线程块拥有一块Shared Memory,最后网格(Grid)中所有的线程都可以访问同一块Global Memory,虽然Shared Memory比Global Memory小,但是读写速度却比Global Memory快很多;除此之外,还有两种可以被所有的线程访问的只读存储器:Constant Memory和Texture Memory.

GPU执行CUDA程序时,执行内核的线程(Thread)被组织成线程块(Block),线程块又组成Grid. 这样同一个Kernel程序可以并行运行在一个网格所包括的所有线程块中的线程上. 目前,同一网格内的Block不可以相互通信,只能通过Global Memory共享数据,而同一个线程块中的线程可以通过Shared Memory通信,也可以同步.

对于TSM-RT算法,由于每根射线的追踪过程是相互独立的. 因此,非常适合利用GPU进行并行加速,将每根射线分配给一个GPU线程,一个GPU线程用于计算相应射线的传播路径,并计算相应的远区散射场,所有线程执行相同的操作. 最后,将所有射线对应的散射场累加得到散射总场,进而计算得到雷达散射截面积(Radar Cross-Section,RCS). 基于GPU的TSM-RT算法的基本流程如图3所示.

图3 基于GPU的TSM-RT算法基本流程

由图3可以看出,对于基于GPU的并行TSM-RT算法,首先分配CPU和GPU端的内存,并在CPU上进行海面建模. 然后将海面信息传输到GPU端用于并行计算. 并行计算部分主要分为四部分:划分射线、射线追踪、计算散射场以及散射场规约求和. 其中,每根射线由一个线程代替,所有线程并行计算,得到每个大三角面元上的散射场. 最后,利用规约算法计算得到总散射场,并将计算结果传回CPU计算最终的远区散射场进而得到远区RCS. 对于电大尺寸海面散射问题,往往需要较大内存来存储海面信息,因此Global Memory被用来存储海面信息.

2 仿真结果与讨论

本节首先将基于CPU的串行TSM-RT算法与传统RT算法的计算结果以及计算时间进行对比,证明TSM-RT算法的正确性以及高效性. 然后利用基于GPU的TSM-RT计算三维电大尺寸海面电磁散射,并将计算结果与基于CPU的TSM-RT的计算结果进行对比,验证并行TSM-RT算法的正确性. 同时将基于GPU和CPU的TSM-RT算法的计算时间进行对比.

三维海面采用蒙特卡洛方法进行建模,海谱采用Elfouhaily谱[11]. 实验主机采用Intel i3双核的2.93 GHz CPU,配置Nvidia Geforce GTX 570显卡,程序运行环境为Microsoft Visual Studio 2010 (release). 相应的GPU和CPU参数如表1所示.

表1 GPU和CPU参数

首先将基于CPU的串行TSM-RT算法与传统RT算法的计算结果进行对比,如图4所示,其中海面尺寸为30 m×30 m,每个大三角面元由16个小三角面元组成. 入射波频率为f=1 GHz. 海水的相对介电参数为εr=(73.608 7,54.581 6),入射角度从0°～80°,入射方位角φ=0°,海面上方风速为u10=5 m/s.

(a) HH极化

(b) VV极化图4 基于CPU的串行TSM-RT算法与传统RT算法的20个三维海面样本后向散射RCS计算结果对比

由图4可以看出,基于CPU的串行TSM-RT算法与传统RT算法计算结果吻合的较好,验证了TSM-RT算法的准确性. 另外,随着入射角度的增大,海面的后向散射RCS也不断减小.

表2给出了相应的传统RT与基于CPU的串行TSM-RT算法的计算时间对比,其中该计算时间为81个入射角度的总计算时间.

表2 传统RT与基于CPU的串行TSM-RT算法的计算时间对比

由表2可以看出,与传统的RT算法相比,基于CPU的TSM-RT算法的计算时间减少了很多,对于HH极化和VV极化两种情况,相应的加速比达到49.6和48.96,获得了很好的加速比.

图5分别采用基于GPU的并行TSM-RT以及基于CPU的串行TSM-RT计算20个三维海面样本后向散射RCS,其中海面尺寸为18 m×18 m,每个大三角面元由9个小三角面元组成. 其他参数与图4相同.

(a) HH极化

(b) VV极化图5 基于GPU和CPU的TSM-RT的20个三维海面样本后向散射RCS对比结果

由图5可以看出,基于GPU和CPU的TSM-RT的计算结果吻合非常好. 随着入射角度的增加,海面的后向散射RCS不断减小. 另外,随着海面风速的增大,海面粗糙度也随之增大,相应的漫散射增强. 因此,大风速时的后向散射RCS也比小风速的时候大.

表3为基于GPU和CPU的TSM-RT计算时间对比结果,其中海面尺寸为18 m×18 m,风速分别为u10=5 m/s和u10=10 m/s,该计算时间为单个海面样本后向散射RCS共81个入射角度的计算时间. 基于GPU的TSM-RT算法中,线程块大小为128,线程块个数为625.

表3 基于GPU和CPU的TSM-RT算法计算时间对比

由表3可以看出,与基于CPU的串行TSM-RT算法相比,基于GPU的并行TSM-RT加速算法的计算时间减少了很多. 对于风速分别为u10=5 m/s和u10=10 m/s时,相应的HH极化和VV极化的后向散射RCS加速比分别达到了101.96、96.85、101.85以及96.17,因此,获得了很好的加速效果. 这些均得益于GPU强大的并行处理能力.

3 结 论

本文首先介绍了一种近似RT算法——TSM-RT算法,该算法将粗糙海面划分为一系列大三角面元,每个大三角面元又由许多小三角面元组成. 大三角面元用来近似确定射线的路径,而小三角面元则用于求远区散射场. 与传统的RT算法相比,在保证计算精度的前提下,TSM-RT算法能够有效减少射线与面元的求交次数,因此相应的计算时间也大大减少,进而提高了计算效率.

另外,为了进一步提高计算效率,本文还利用GPU强大的并行处理能力对该算法进行加速,对于TSM-RT算法,每条射线的追踪过程都是相互独立的,非常适合利用GPU的并行处理能力进行加速,因此本文提出了基于GPU的TSM-RT算法,与基于CPU的TSM-RT算法相比,计算时间减少了很多,取得了良好的加速效果.

[1] 中华人民共和国国土资源部.2008年国土资源公报[EB/OL].[2015-07-25].http://www. Mlr.Gov.cn/wszb/2009/20090331bzzbhxdzzk/beijingziliao/200903/t20090331687345.htm.2009.

[2] HARRINGTON R F. Field computation by moment methods [M]. NewYork: Macmillan, 1968.

[3] BARKA A, CAUDRILLIER P. Domain decomposition method based on generalized scattering matrix for installed performance of antennas on aircraft[J]. IEEE transactions on antennas and propagation, 2007, 55(6): 1833-1842.

[4] GRIESSER T, BALANIS C A. Backscatter analysis of dihedral corner reflectors using physical optics and the physical theory of diffraction[J]. IEEE transactions on antennas and propagation, 1987, 35(10): 1137-1147.

[5] DEHMOLLAIAN M, SARABANDI K. Electromagnetic scattering from foliage camouflaged complex targets[J]. IEEE transactions on geoscience remote sensing, 2006, 44(10): 2698-2709.

[6] 周季夫, 钟诚文, 尹世群, 等. 基于GPGPU的Lattice-Boltzmann数值模拟算法[J]. 计算机辅助设计与图形学学报, 2008, 20(7): 912-918.

ZHOU J F, ZHONG C W, YIN S Q, et al. Numerical simulation algorithm of Lattice-Boltzmann on GPGPU[J]. Journal of computer-aided design and computer graphics, 2008, 20(7): 912-918. (in Chinese)

[7] 吴恩华, 柳有权. 基于图形处理器(GPU)的通用计算[J]. 计算机辅助设计与图形学学报, 2004, 16(5): 601-612.

WU E H, LIU Y Q. General purpose Computation on GPU[J]. Journal of computer-aided design and computer graphics, 2004, 16(5): 601-612. (in Chinese)

[8] 曹锋, 周傲英. 基于图形处理器的数据流快速聚类[J]. 软件学报, 2007, 18(2): 291-302.

CAO F, ZHOU A Y. Fast clustering of data streams using graphics processors[J]. Journal of software, 2007, 18(2): 291-302.(in Chinese)

[9] Internet Draft Nvidia Corporation. NVIDIA CUDA compute unified device architecture programming guide 1.1. [EB/OL] .2008[2015-07-25]. http://developer. Nvidia.com/object/cuda-get.html.

[10] XU F, JIN Q. Bidirectional analytic ray tracing for fast computation of composite scattering from electric-large target over a randomly rough surface[J]. IEEE transactions on antennas and propagation, 2009, 57(5): 1495-1505.

[11] ELFOUHAILY T, CHAPRON B, KATSAROS K, et al. A unified directional spectrum for long and short wind-driven waves[J]. Journal of geophysics research: oceans (1978—2012), 1997, 102(C7): 15781-15796.

孟肖 (1989-),女,陕西人,西安电子科技大学物理与光电工程学院博士研究生,研究方向为电大尺寸海面电磁散射计算及基于GPU的高性能并行加速技术研究.

郭立新 (1968-),男,陕西人,西安电子科技大学物理与光电工程学院博士生导师,研究方向为雷达通信环境中的波传播与散射、地物环境遥感与仿真、目标与环境光电特性分析及应用、空间等离子体探测与信息处理等.

黄青青 (1989-),女,贵州人,西安电子科技大学物理与光电工程学院硕士研究生,研究方向为随机粗糙面电磁散射特性研究.

李娟 (1984-),女,山西人,西安电子科技大学物理与光电工程学院副教授,研究方向为随机粗糙面与目标的复合电磁散射研究.

EM scattering from the sea surface based on the parallelized two scale model ray tracing

MENG Xiao GUO Lixin HUANG Qingqing LI Juan

(SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710071,China)

This paper aims at the fast computation of the electromagnetic scattering from the large-scale sea surface by an approximate ray tracing(RT) method which is based on the two scale model(TSM-RT). Compared with the traditional RT method, TSM-RT method can decrease the number of intersections between the rays and facets, and keep a good accuracy. Therefore the computational efficiency is greatly improved. In addition, the parallelized accelerated TSM-RT method based on the graphics processing unit(GPU) is utilized in order to further improve the efficiency. According to the computational results, it demonstrates that the computational time of the GPU-based TSM-RT method is greatly decreased compared with the CPU-based TSM-RT method, therefore a good speedup ratio is achieved.

TSM-RT method; GPU; parallelized accelerated TSM-RT

10.13443/j.cjors.2015072502

2015-07-25

自然科学基金杰出青年科学基金(6125002)； 中央高校业务费； 国家自然青年基金(61501360)

TN958

A

1005-0388(2016)04-0725-06

孟肖, 郭立新, 黄青青, 等. 基于并行双尺度射线追踪的海面电磁散射计算[J]. 电波科学学报,2016,31(4):725-730.

MENG X, GUO L X, HUANG Q Q, et al. EM scattering from the sea surface based on the parallelized two scale model ray tracing[J]. Chinese journal of radio science,2016,31(4):725-730. (in Chinese). DOI: 10.13443/j.cjors.2015072502

联系人： 孟肖 E-mail: mengxxidian@126.com