大型FPSO上层建筑吊装强度有限元分析
周 庆,向小斌,王初龙,龚伟兵
(上海中远船务工程有限公司,上海 200231)
大型FPSO上层建筑吊装强度有限元分析
周 庆,向小斌,王初龙,龚伟兵
(上海中远船务工程有限公司,上海 200231)
通过SESAM/GeniE软件对总重达1 800 t的FPSO上层建筑整体吊装进行有限元仿真分析,计算载荷按照DNV规范选取,通过计算得到整个上层建筑在吊装中的结构响应。计算中模拟了钢丝绳索具,从而能更准确地计算吊耳的应力和变形,同时还能够计算得到浮吊的每个钩头的实际载荷,保证单个钩头载荷不超载。有限元计算为上层建筑整体吊装方案的可行性提供了依据,计算结果可以用来优化吊装方案及指导局部加强措施,从而保证整体吊装的顺利进行。
FPSO;上层建筑吊装;强度分析;有限元
0 引言
上层建筑整体吊装在船舶与海洋工程建造中应用较广,国内外一些大型海洋工程船舶和平台的上层建筑通常采用模块化的建造方法,以大大提高预舾装率,上层建筑整体吊装能够显著提高劳动生产效率和建造进度。然而大型海洋工程船舶与平台的上层建筑因为设计定员较多,整体重量要远远大于常规船舶的上层建筑,整体吊装难度也相应增大。近年来随着船厂吊装设备能力的提高和吊装工艺的逐步改进,吊装的上层建筑的尺寸和重量也越来越大,如何检验吊装方案的合理性,保证吊装安全可靠成为一个关键问题。近年来,应用有限元法对吊装过程进行数值仿真分析,成为上层建筑整体吊装的重要研究课题,李永正[1]等利用有限元法计算了大型油船上层建筑吊装前和吊装时的结构响应,袁红莉等[2]及王峰等[3]对大型船舶上层建筑整体吊装的工艺进行了研究,并应用有限元计算进行验证。
本文依据DNV规范[4],以某大型FPSO的上层建筑为研究对象,利用有限元软件SESAM/GeniE,对重达1 800 t的FPSO上层建筑的整体吊装进行数
值仿真分析,计算了上层建筑吊装过程中的应力和变形,验证了吊装方案的可行性。
1 上层建筑基本情况和有限元模型
1.1 上层建筑基本情况
该大型FPSO上层建筑设计定员为110人,共分七层,从上至下分别为顶甲板、四甲板、三甲板、二甲板、一甲板、艉楼甲板和中间甲板,整个上层建筑长41.4 m、宽13.5 m、高23.5 m。所有结构均采用AH36高强度钢建造,材料许用应力为355 MPa,材料密度为ρ=7.85×103kg/m3,弹性模量为E=2.05×1011,泊松比 v=0.3,整个模块的重量重心如表1所示。
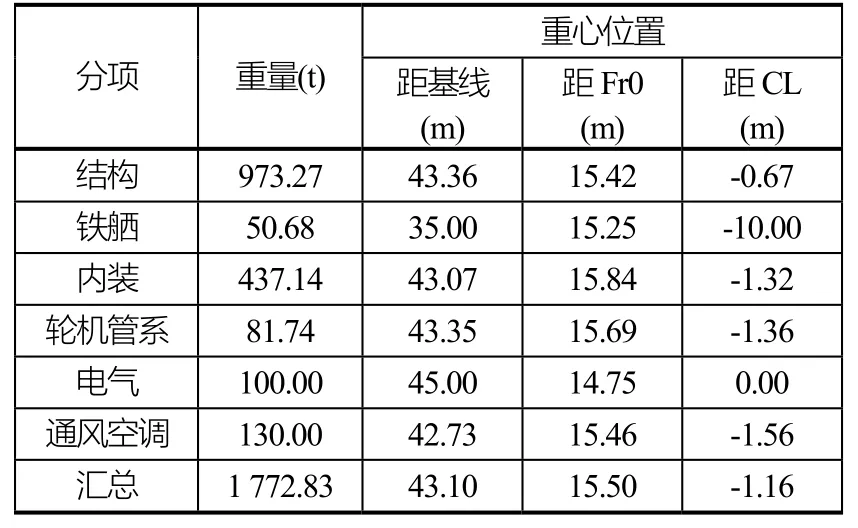
表1 模块的重量重心
1.2 吊装方案
该上层建筑采用某2 000 t浮吊吊装,该浮吊有四个500 t主钩,相对应的在上层建筑上布置了四组吊点,每组8个吊耳,一共32个吊耳。吊耳布置于上层建筑的艏艉两侧,以前后围壁的上端为吊耳眼板,吊耳通过钢丝绳、滑轮等与浮吊钩头连接,如图1所示。
图1 吊耳布置
1.3 有限元模型
利用SESAM/GeniE有限元计算软件建立整个上层建筑的结构有限元模型,如图2和图3所示。甲板、舱壁、纵桁及横梁的腹板采用板单元建模,纵桁和横梁的面板、甲板纵骨及舱壁扶强材等采用梁单元建模,钢丝绳用杆单元建模。上层建筑结构纵骨间距为900 mm,总体网格尺寸为450 mm×450 mm,即每个纵骨间距两个网格,吊耳附近区域细化网格尺寸为50 mm×50 mm。分析计算采用公制单位,长度单位为m,力的单位为N,应力单位为Pa(N/m2)。

图2 显示板厚的整体有限元模型

图3 显示板厚的局部有限元模型
1.4 坐标系、边界条件及载荷工况
坐标系定义:采用右手法则,定义Fr0与基线和中线的交点为坐标原点,x轴为沿船长方向,指向船首为正,y轴为沿船宽方向,指向左舷为正,z方向向上为正。
边界条件:所有吊点钢丝绳索具末端约束x、y、z三个方向位移,另外在有限元模型上通过理论重心的截面上选取两个节点,一个节点位于横向结构上,约束它的x方向位移,另外一个节点位于纵向结构上,约束它的y方向位移,如图4所示。本文中使用杆单元模拟钢丝绳索具是为了计算钢丝绳的支反力,从而计算四钩头浮吊每个钩头的实际分担
载荷,防止单个钩头超载。

图4 边界条件
载荷工况:表1中的结构分项重量由软件根据模型自动生成,其它分项重量通过设备单元分层施加在上层建筑各层甲板上。根据DNV规范[4],吊装有限元计算需要考虑吊装作业的动态放大效应、重量偏差、重心偏移、索具偏差等因素影响,对吊装载荷进行修正,载荷修正系数如表2所示。因为表1中重量重心数据已经包含10%的余量,所以表2中重量偏差和重心偏移修正值均取1.00。

表2 重量偏差和重心偏移修正值
除了上述吊装作业载荷修正系数以外,DNV规范[4]还针对吊装结构的结构分类,规定了额外的载荷系数如表3所示。

表3 载荷系数
综合表 2和表 3,可得最大的载荷系数为1.31×1.7=2.227,对应的AH36高强钢材料许用应力为355/2.227=159.4 MPa。
2 有限元计算
根据DNV规范[4],采用许用应力法进行吊装计算,计算得到的应力和变形分布见图5~图8所示。

图5 整体应力分布

图6 整体位移分布
3 结果分析
整理各部位的最大应力和变形结果如表4所示,由结果可见,整个结构应力均未超过DNV规范[4]许用应力要求,结构强度满足吊装要求。

表4 各部位的最大应力和变形结果
从图7中可见,吊装引起的高应力除了分布在吊耳区域外,一些门窗开孔的角隅部位应力值也相对很大,最大应力155.4 MPa发生在吊点下方强支撑结构上,如图9所示。该处结构根据初次计算结果,经过加强处理后,最终的应力结果满足了许用应力要求。

图9 最大应力位置
为了保证吊装作业中浮吊单个钩头不超载,使用杆单元模拟了钢丝绳,计算结果中可以方便地提取这些杆单元的支反力,如图10所示。

图10 吊点钢丝绳支反力
通过计算每组吊点的8根钢丝绳支反力之和,可以得到每个钩头的实际分担载荷,计算得到四组吊点对应的钩头载荷,如表5所示。
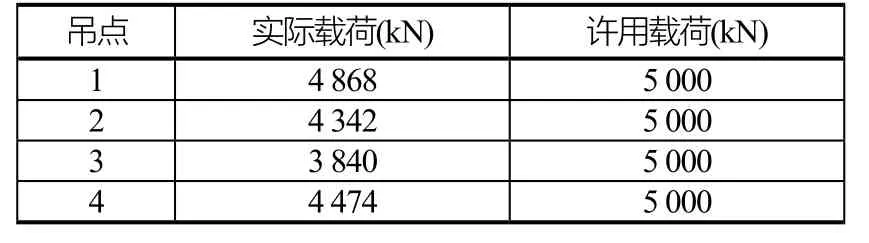
表5 四组吊点对应的钩头载荷
4 结论
本文根据DNV规范[4],通过有限元方法,对总重达1 800 t的FPSO上层建筑整体吊装进行了数值仿真分析。通过有限元计算,得到该上层建筑结构吊装时的结构响应,同时对钢丝绳索具进行了模拟,通过钢丝绳支反力来校核浮吊单个钩头的载荷。
通过对计算结果的分析可知,吊装时的最大应力容易出现在吊点的强支撑结构上以及吊点附近的开口角隅部位。通过有限元计算可以提前发现问题,并根据结构特点采取相应的加强措施,以保证加强后的局部强度满足吊装要求,保证整体吊装作业的顺利安全进行。
[1]李永正, 王珂, 郭玮.大型油船上层建筑整体吊装强度有限元分析[J].科学技术与工程, 2012, 12(36): 10011-10016.
[2]袁红莉, 蔡振雄, 陈章兰.53 000DWT散货船上层建筑整体吊装工艺设计[J].船舶工程, 2009,31(2): 1-3.
[3]王锋, 汪家政.大型船舶上层建筑整体吊装技术研究及应用[J].造船技术, 2011, 299(1): 20-22.
[4]DNV.Rules for Planning and execution of Marine Operations[S].2000.
[5]中国船级社.船体结构强度直接计算指南[S].北京:人民交通出版社, 2001.
FEM Analysis of Lifting Strength of Large FPSO Super-structure
Zhou Qing, Xiang Xiao-bin, Wang Chu-long, Gong Wei-bing
(COSCO Shanghai Shipyard Co., Ltd., Shanghai 200231, China)
By the software SESAM/GeniE, the FEM analysis is performed to simulate and analyze the strength for the lifting of large FPSO super-structure of 1 800 t.The loads are applied according to the rule of DNV and the structural response caused by lifting can be obtained.The lifting slings are also simulated to accurately calculate the response of lifting pad-eyes.Meanwhile, the load of each hook of lifting barge can be calculated to avoid overload.The FEM calculation offers basis for the feasibility of the lifting scheme of the super-structure.The calculating result can be used to optimize the lifting scheme and to guide part enhancement measure, which guarantees the lifting work goes smoothly.
FPSO; super-structure lifting; strength analysis; finite element
U663.6
A
10.14141/j.31-1981.2016.02.004
周庆(1974—),男,硕士,工程师,研究方向:船舶与海洋工程结构设计与分析。

