页岩气有机质纳米孔气体传输微尺度效应

吴克柳 李相方 陈掌星

页岩气有机质纳米孔气体传输微尺度效应

吴克柳1,2李相方2陈掌星1,2

1.Department of Chemical and Petroleum Engineering, University of Calgary 2.中国石油大学石油工程教育部重点实验室

页岩气有机质孔隙多为纳米尺度且气体赋存方式多样，因此页岩气有机质纳米孔中的气体存在多种传输机理，而如何建立能描述高压条件下所有传输机理的纳米孔体相气体传输模型、如何描述页岩有机质纳米孔表面扩散，以及确定表面扩散对气体传输贡献究竟有多大等则是目前亟待解决的难题。为此，综合考虑体相气体传输、表面扩散、真实气体、吸附层和应力敏感等微尺度效应的影响，建立了页岩气有机质纳米孔气体传输模型。研究结果表明：①通过滑脱流动和努森扩散加权叠加建立的体相气体传输模型能合理描述体相气体传输；②表面扩散是重要的传输机理，尤其在尺度小的纳米孔中，主宰了气体传输；③页岩气应力敏感效应不同于常规油气藏，其不仅与有机质力学属性、有效应力等有关，而且还与气体传输机理有关。结论认为，所建模型能够从室内低压条件直接推广到页岩储集层高压条件，能为页岩气生产动态分析、产能预测和生产制度制订提供指导。

页岩气 有机质孔隙 纳米级孔隙 微尺度 滑脱流动 努森扩散 表面扩散 应力敏感

据统计，世界页岩气资源量为636.283×1012m3，相当于煤层气和致密砂岩气的总和[1]。北美页岩气经济高效规模开发，成为北美天然气供应的重要来源，并引起全球天然气供应格局的重大变化[2]。中国初步预测页岩气资源量为30×1012～166×1012m3[3]，2014年中国石化涪陵页岩气产量突破10×108m3，取得了巨大成功，表明中国页岩气高效开发是可能的。为了实现中国能源安全目标，适合于中国页岩气高效开发的理论和技术急需突破。

与常规油气藏相比，页岩孔隙度和渗透率异常低，孔隙度普遍低于10%，渗透率在纳达西与微达西之间[4]。不同于常规油气的运移成藏，页岩气是自生自储型气藏，自由气、吸附气和溶解气共存[4]。吸附气占总气量的比例高，介于20%～80%[4]。页岩孔隙多尺度特征和气体赋存方式多样性，造成页岩气体传输机理异常复杂[5]，有机质纳米孔气体传输需分为纳米孔体相气体传输和吸附气表面扩散[6-7]。

由于微尺度效应，描述常规尺度流动的方程不再适用[8-11]。页岩体相气体在纳米孔壁面气体速度不再为零，发生滑脱流动和努森扩散，经典达西定律无法描述。典型页岩气藏条件下，努森数介于0.000 2～6.000 0（努森数是气体平均分子自由程与孔隙特征长度的比值）。因此，微尺度下体相气体传输机理包括连续流动、滑脱流动和过渡流[12]。统计数据表明，北美页岩气藏埋深普遍为500～3 000 m，地层压力为5～30 MPa[13]。而中国页岩气埋深介于300～6 000 m, 压力高达60 MPa[14]。高压条件加剧气体传输的微尺度效应：高压使气体更稠密，分子间范德华力增大，影响气体传输；且在纳米孔狭窄空间中，气体分子不能看作一个点，需考虑分子自身体积对气体传输的影响[15]。目前，大多数模型无法考虑高压气体稠密效应的影响，即使低压条件，也不能合理方便地描述体相气体所有传输机理。Klinkenberg模型仅适用于低压气体连续流动和滑脱流动[16]；尘气模型将扩散量和水动力流量任意叠加，未考虑两者的耦合[17]；Beskok和Karniadakis 模型仅适合努森数小于“1” 情况，且含有经验系数[18]；Javadpour 模型为滑脱流动和努森扩散线性相加，也未考虑两者的耦合[19]；Anderson 等提出的模型虽能描述低压条件下所有传输机理，但含经验系数，需实验数据确定[20]。吴克柳等人揭示了页岩复杂孔裂隙真实气体传输机理，并提出了数学模型，研究结果表明高压条件下气体传输不同于低压条件下气体传输[21]。因此，急需开发出简单的，且能描述高压条件下所有传输机理的页岩纳米孔体相气体传输模型。

由于微尺度效应，吸附气占据纳米孔隙的空间不可忽略，其对体相气体传输影响很大[7]。同时，吸附气自身发生表面扩散，浓度梯度是表面扩散的驱动力[22]，页岩有机质纳米孔壁面吸附气浓度梯度大[23]，且具有巨大比表面积[24]。因此，表面扩散作为重要的传输机理，也不可忽略[25-27]。很多学者研究表明，由于发生表面扩散，纳米孔表观渗透率预测值是常规水动力学方法预测值的10倍[28]，甚至更高出几个数量级[29-30]。由于微尺度效应，体相气体传输可能很弱，尤其在纳米孔网络未充分发育的页岩区域[7]，表面扩散甚至主宰气体传输[31]。页岩有机质纳米孔表面扩散如何描述，表面扩散对气体传输贡献多大，是人们关注的一项重要工作。

页岩降压开发过程中，有效应力增大，发生应力敏感。与砂岩相比，页岩有机质强度弱，更易变形，应力敏感更强[4,32]。众多学者的实验研究结果表明，孔隙度仅略微减小，而渗透率的下降幅度却超过两个数量级[32-34]。与常规油气藏相比，由于页岩气微尺度效应显著，且发生表面扩散，应力敏感效应具有特殊性[35]，不能将常规油气藏应力敏感理论研究出的结果直接应用于页岩气开发分析中[4]。对于我国，页岩气埋藏深，有机碳含量和热成熟度高[36-37]，应力敏感显著[38]。因此，考虑应力敏感效应影响，对我国页岩气开发显得尤为重要。

笔者首先建立页岩有机质纳米孔体相气体传输模型和吸附气表面模型，并综合考虑微尺度效应，包括体相气体滑脱流动和努森扩散、吸附气表面扩散、真实气体效应、吸附层和应力敏感效应。通过模型描述，厘清各种传输机理相互关系和不同微尺度效应对气体传输影响。然后用实验和分子模拟数据验证模型。最后详细探讨微尺度效应对页岩气体传输的影响。

1 模型建立

分别建立页岩有机质纳米孔体相气体传输模型和壁面吸附气表面扩散模型，同时推导出真实气体效应、吸附层和应力敏感效应影响的数学模型。

1.1 体相气体传输

页岩典型储集层条件下，努森数介于0.000 2～6.000 0[12]。因此，页岩气体传输机理包括连续流动、滑脱流动和过渡流动[39]。在特定压力和温度条件下，气体传输机理一个或者多个共存。为了应用方便，需要一个综合性的本构方程来合理描述所有这些传输机理。核心问题是这些传输机理占总传输份额的描述。为此，笔者基于滑脱流动和努森扩散两种传输机理，分别以分子之间碰撞频率和分子与壁面碰撞频率占总碰撞频率的比值作为滑脱流动和努森扩散的权重系数，进行权重相加，建立了页岩纳米孔体相气体传输模型。

在低压条件下，页岩气可看作理想气体，则纳米孔体相理想气体总传输量为[9]：

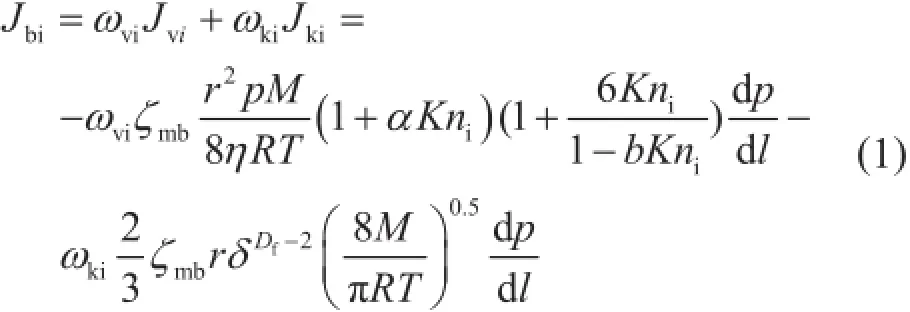
式中Jbi表示体相理想气体总质量流量，kg/ (m2·s)；Jvi表示理想气体滑脱流动质量流量，kg/ (m2·s)；Jki表示理想气体努森扩散质量流量，kg/ (m2·s)；ωvi表示理想气体滑脱流动权重系数，无因次；ωki表示理想气体努森扩散权重系数，无因次；ξmb表示页岩纳米孔体相气体传输修正系数，无因次；r表示有效应力下的孔隙半径，m；p表示气体压力，MPa；M表示气体摩尔质量，kg/mol；η表示气体黏度，Pa·s；R表示气体常数，J/(mol·K)；T表示地层温度，K；α表示气体稀有效应系数，无因次；Kni表示理想气体对应的努森数，无因次；b表示气体滑脱常数，无因次；l表示气体传输方向的距离，m；δ表示分子直径与局部孔隙直径的比值，无因次；Df表示孔隙壁面分形维数，无因次。

在高压条件下，气体分子间相互作用力和气体分子自身体积对气体传输的影响不可忽略。这种真实气体效应的影响可通过真实气体偏差因子、黏度和平均分子自由程对气体传输的影响来描述。则考虑真实气体效应的纳米孔体相气体总传输量为：

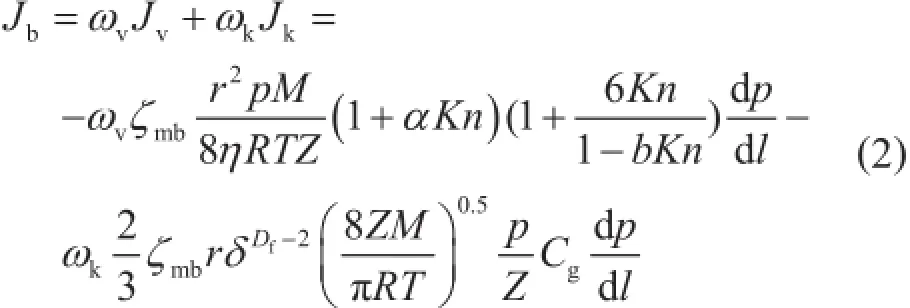
式中Jb表示体相真实气体总质量流量，kg/ (m2·s)；Jv表示真实气体滑脱流动质量流量，kg/ (m2·s)；Jk表示真实气体努森扩散质量流量，kg/ (m2·s)；ωv表示真实气体滑脱流动权重系数，无因次；ωk表示真实气体努森扩散权重系数，无因次；Z表示气体偏差因子，无因次；Kn表示真实气体对应的努森数，无因次；Cg表示气体压缩因子，1/MPa。

1.2 壁面吸附气吸附/解吸附

页岩气初始条件下，纳米孔表面吸附气和体相气体呈平衡态，吸附气量可用Langmuir等温吸附表达[40]。页岩气降压开发，尽管吸附气发生了表面扩散，但由于吸附/解吸附是很快的物理过程。因此，仍可用Langmuir等温吸附表达吸附气量[26]，即

式中qai表示单位质量页岩理想吸附气体的标准体积，m3/kg；qL表示Langmuir体积，m3/kg；pL表示Langmuir压力，MPa。

当考虑真实气体效应的影响，吸附气量可表达为[39]：

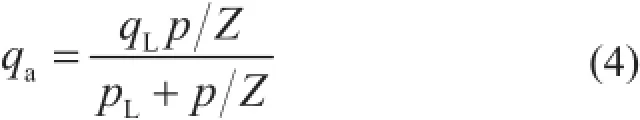
式中qa表示单位质量页岩真实吸附气体的标准体积，m3/kg。

由于Langmuir吸附为单层吸附，因此气体覆盖度可定义为吸附量与Langmuir体积的比值，则理想气体和真实气体覆盖度分别为：

式中θi表示理想气体在纳米孔壁面的覆盖度，无因次；θ表示真实气体在纳米孔壁面的覆盖度，无因次。

吸附气的存在，占据纳米孔部分空间，则体相理想和真实气体传输的纳米孔有效半径分别为：

式中radi表示理想气体纳米孔有效半径，m；rad表示真实气体纳米孔有效半径，m；dm表示气体分子直径，m。

1.3 壁面吸附气表面扩散

吸附气除了吸附/解吸附，还发生表面扩散。表面扩散驱动力是吸附气浓度梯度[23]，可通过体相气体的压力梯度表达，则纳米孔理想气体表面扩散量为：

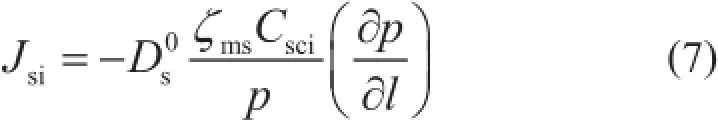
式中Jsi表示理想气体表面扩散质量通量，kg/(m2·s )；表示气体覆盖度为“0”的表面扩散系数，m2/s；ξms表示页岩纳米孔表面气体扩散修正系数，无因次；Csci表示理想吸附气浓度，kg/m3。

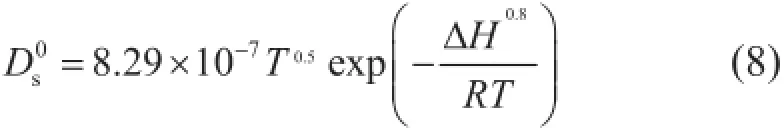
式中ΔH表示等量吸附热，J/mol。

式（8）的表面扩散系数是在低压条件下通过理论和实验获得的，与压力无关。因此，仅适用于低压条件下的气体表面扩散。为了描述高压条件下的气体表面扩散，需考虑气体覆盖度对表面扩散的影响，Chen和Yang利用动力学方法推导了考虑覆盖度影响的表面扩散系数为[43]：

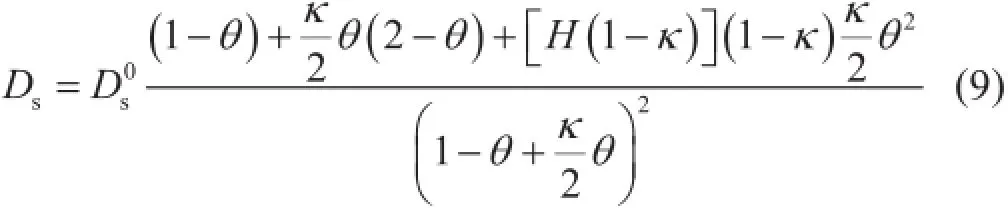
其中

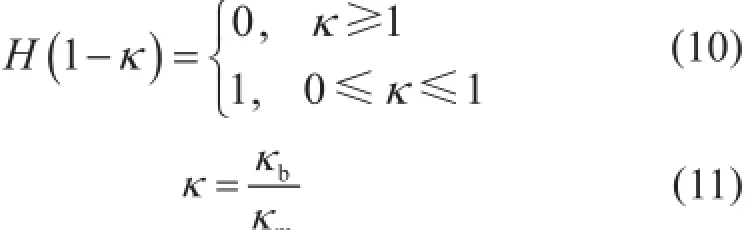
式中Ds表示真实气体表面扩散系数，m2/s；H(1-κ)表示Heaviside函数，无因次；κ表示表面气体分子阻塞系数，无因次；κm表示表面气体分子前进速度常数，m/s；κb表示表面气体分子阻塞速度常数，m/s。

式（10）和式（11）表明，当κm＞κb，不论运动前方的位置是否已被分子占据，都将发生表面扩散；当κm＜κb，气体分子被堵塞，表面扩散停止，但堵塞现象不会造成气体分子的逆扩散。

依据式（5），页岩纳米孔壁面Langmuir单层吸附的理想和真实气体浓度分别为：

式中Csc表示真实吸附气浓度，kg/m3。

根据式（7），结合式（9）和式（12），页岩纳米孔真实吸附气表面扩散模型为：

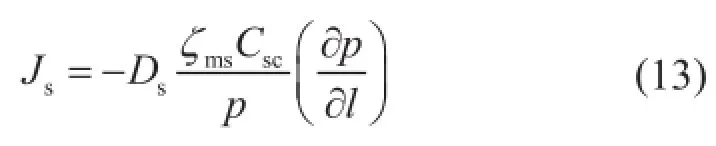
式中Js表示真实气体表面扩散质量通量，kg/(m2·s)。

1.4 应力敏感

页岩降压开发，有效应力增大，发生应力敏感，改变了储集层有效孔隙空间，具体表现为绝对渗透率、孔隙度和纳米孔半径减小，气体传输机理发生变化，传输能力下降。Dong等通过页岩岩心应力敏感测试实验研究表明，幂指数方程能够很好地描述页岩绝对渗透率与孔隙度的应力敏感效应[32]。即

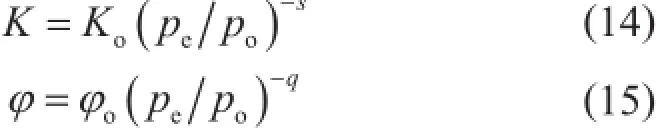
式中K表示页岩有效应力下的绝对渗透率，m2；Ko表示页岩在大气压下的绝对渗透率，m2；pe表示有效应力，MPa；po表示大气压，MPa；s表示页岩渗透率系数，无因次；φ表示页岩有效应力下的孔隙度；φo表示页岩在大气压下的孔隙度；q表示页岩孔隙度系数，无因次。

页岩纳米孔半径与绝对渗透率与孔隙度的关系为[39]：

式中τ表示迂曲度，无因次。

结合式（14）～（16），考虑应力敏感效应的页岩纳米孔半径可表达为：

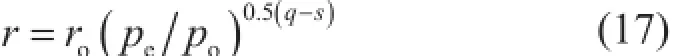
式中ro表示大气压下的孔隙半径，m。

2 模型描述

页岩有机质纳米孔气体传输机理主要包括体相自由气的滑脱流动、努森扩散和吸附气的表面扩散。气体总传输量是由这些传输机理对应的气体传输量组成的[41,44]。其中，吸附气表面扩散量与体相气体传输量可通过简单线性相加，而体相气体的滑脱流量和努森扩散量需加权相加。所以，考虑真实气体效应的有机质纳米孔气体总传输量表达为：

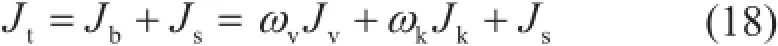
值得说明的是，吸附/解吸附只是体相自由气和吸附气两种赋存状态之间的转换，其对体相气体传输和吸附气表面扩散有影响，但本身对气体传输并无贡献。因此分析气体传输贡献时不需要考虑气体的吸附/解吸附。

模型除了考虑多种传输机理，还考虑了真实气体、吸附层和应力敏感等微尺度效应对气体传输的影响。当页岩降压开发，页岩纳米孔发生应力敏感，孔隙尺度减小，降低了体相气体传输和吸附气表面扩散；同时，吸附气部分解吸，吸附层厚度减小，增大了体相气体传输空间，提高了体相气体传输。

3 模型验证

同时考虑纳米孔体相气体传输和壁面吸附气表面扩散的实验异常复杂，且未找到相关公开发表的实验数据，无法直接验证综合模型可靠性。因此，只能分别验证纳米孔体相气体传输模型和壁面吸附气表面扩散模型，从而间接验证综合模型可靠性。

3.1 体相理想气体传输模型

分子模拟数据准确，常用来验证纳米孔体相气体传输模型[45]。因此，笔者将模型计算结果与公开发表的分子模拟结果进行对比，验证模型可靠性。验证模型计算参数如表1所示。

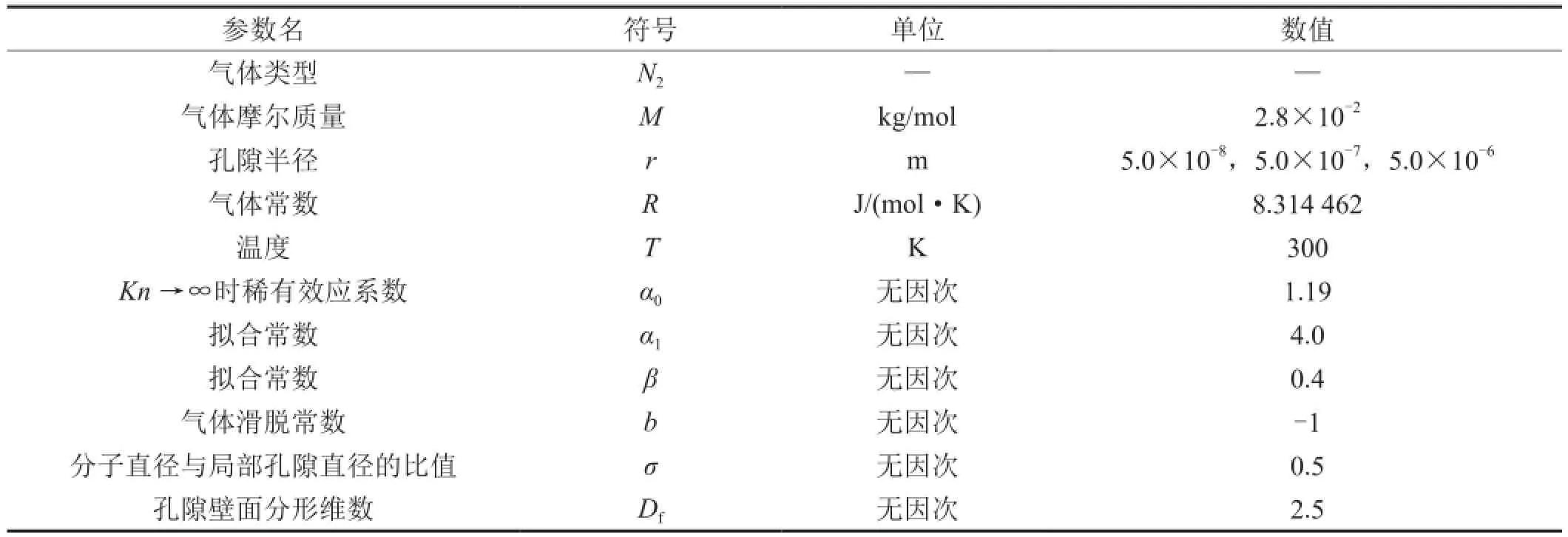
表1 验证体相气体传输模型所需的计算参数表

为了对比方便，分别以连续流流量和努森扩散量为基础，将纳米孔体相理想气体总传输量无因次化，分别表达为：

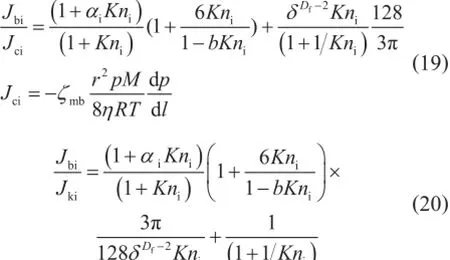
式中Jbi/Jci表示连续流流量为基础的无因次体相理想气体传输量，无因次；Jbi/Jki表示努森扩散量为基础的无因次体相理想气体传输量，无因次；Jci表示理想气体连续流动质量流量，kg/ (m2·s)。

由图1可知，模型解析解与分子模拟结果吻合很好，表明建立的体相理想气体传输模型在模拟低压条件下纳米孔体相稀薄气体的传输是可靠的。

3.2 体相真实气体传输模型

为了验证方便，用真实气体传输模型计算结果与理想气体传输模型计算结果的偏差程度与分子模拟的相应结果进行对比。偏差程度表达为：

由图2可知，模型解析解与分子模拟结果吻合很好，表明建立的体相真实气体传输模型在模拟高压条件下纳米孔体相稠密气体的传输是可靠的。

3.3 壁面吸附气表面扩散模型

由于气体覆盖度为“0”的表面扩散系数（D0s）是基于理论推导和实验数据拟合得出。因此，根据式（8）计算的D0s是可靠的。

为了验证高压条件下考虑吸附气覆盖度影响的表面扩散系数模型的可靠性，将式（9）变形为：

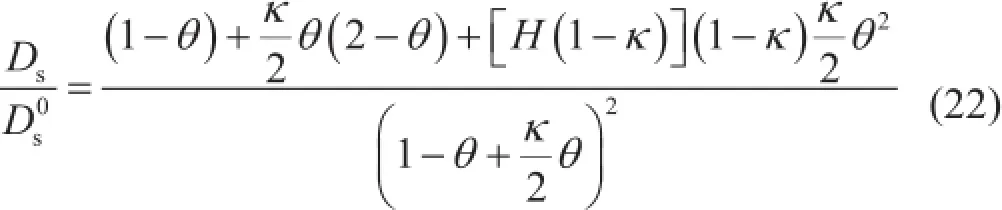
根据式（22）计算的结果与实验数据进行对比，模型解析解与实验数据吻合较好（图3），表明该模型是可靠的，可以应用于高压条件下页岩纳米孔吸附气的表面扩散。其中模型计算参数和实验条件如表2所示。

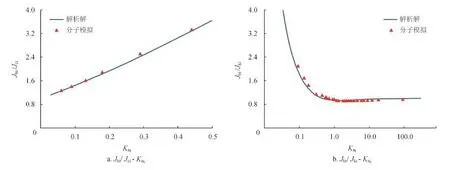
图1 模型解析解与分子模拟的无因次体相理想气体传输量对比图

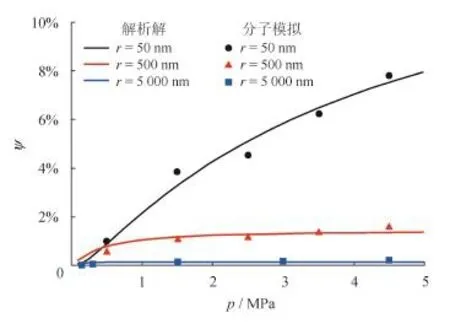
图2 模型解析解与分子模拟的偏差程度对比图

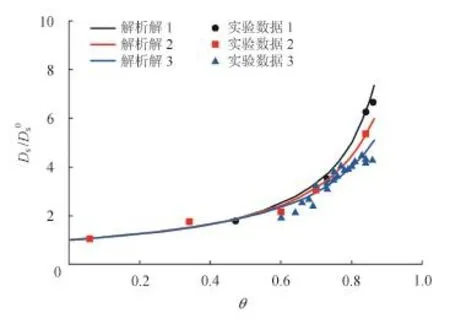
图3 Ds/Ds0与θ的关系曲线图

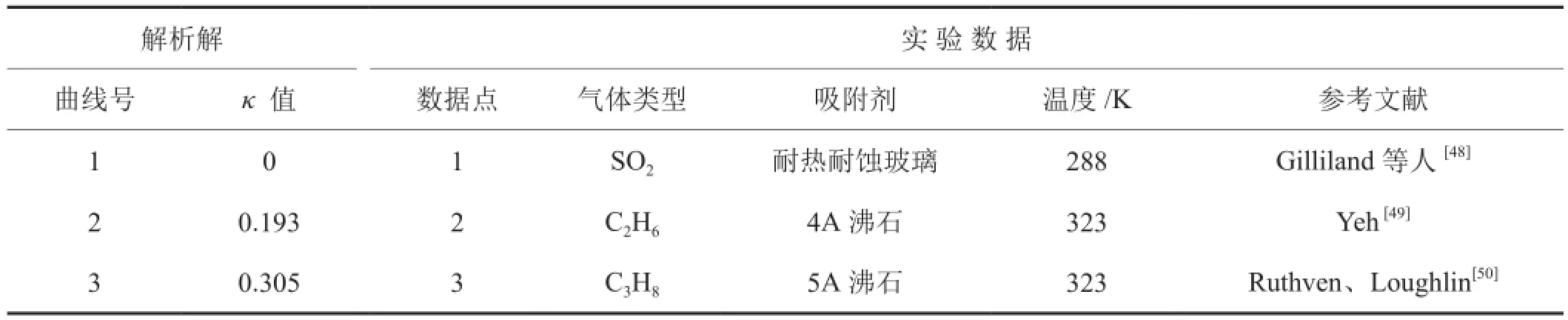
表2 验证吸附气表面扩散模型所需的计算和实验参数表

4 结果与讨论

为了便于讨论不同传输机理对页岩气开发影响，可分别通过相应气体传导率来描述和分析。根据式（2），并考虑权重系数，则考虑真实气体效应的体相气体滑脱流动和努森扩散传导率可分别表达为：

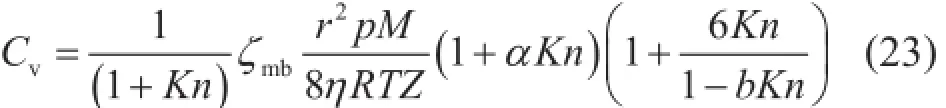
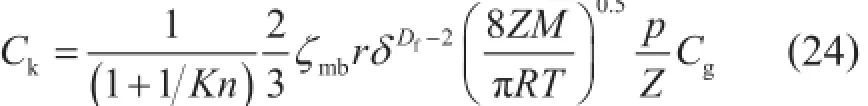
根据式（13），考虑高压条件下的吸附气表面扩散传导率为：

结合式（23）～（24），则页岩纳米孔真实气体传输总传导率为：

模型结果和讨论所需的计算参数如表3所示，计算结果为解析解。

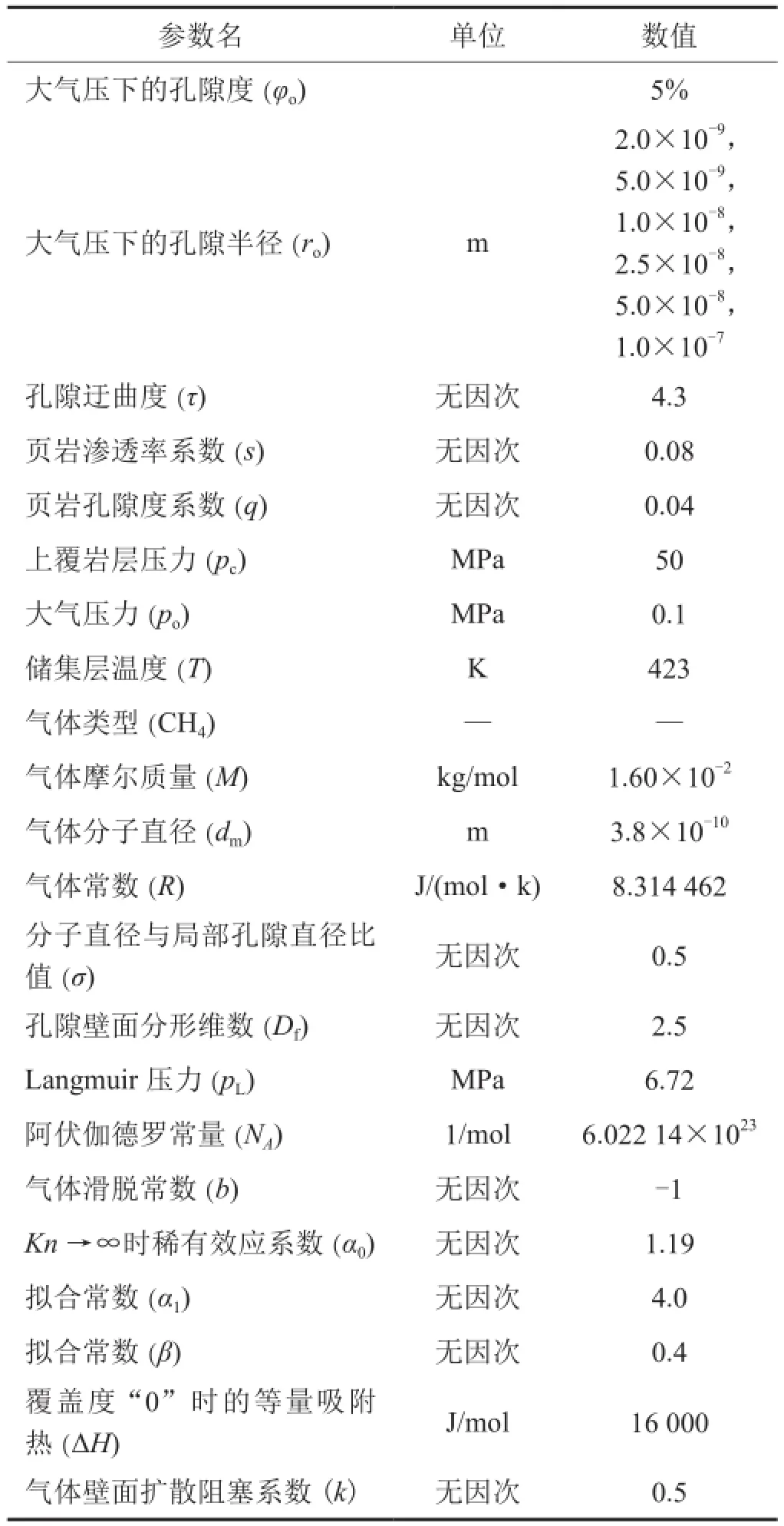
表3 模型结果和讨论所需的计算参数表

4.1 不同传输量对比

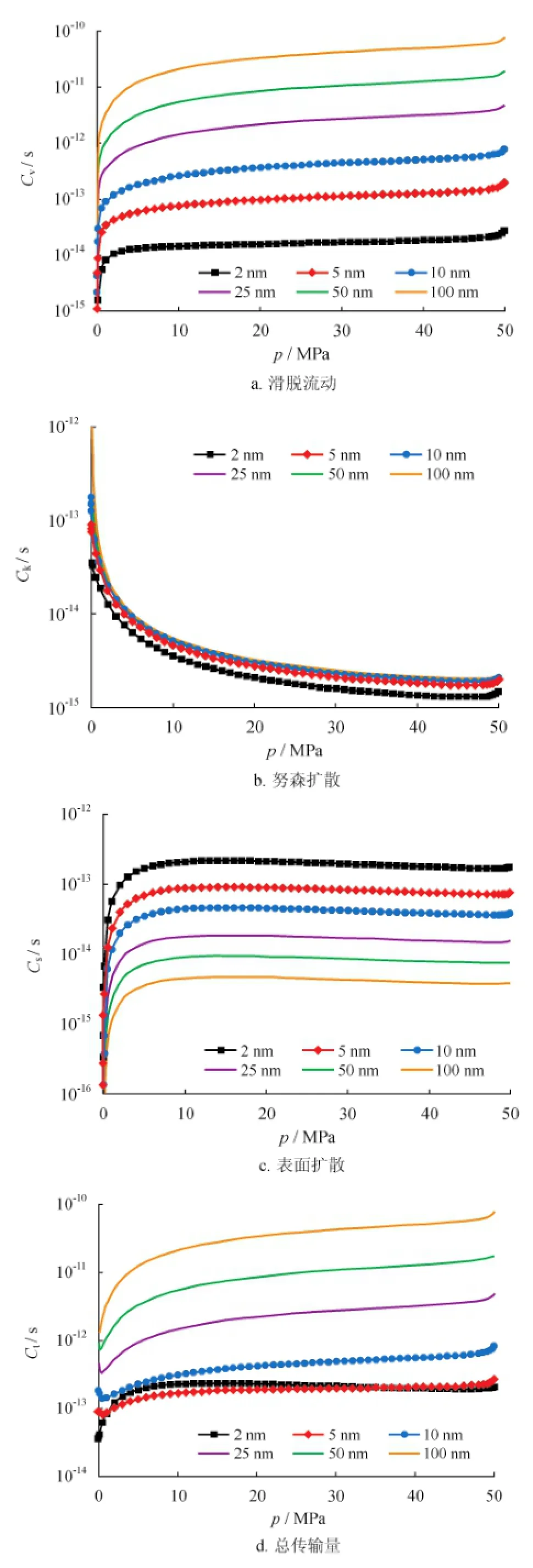
图4 不同传输机理的传导率随压力变化曲线图

页岩气降压开发过程中，滑脱流动权重系数减小，应力敏感效应造成有效孔隙半径减小，因而滑脱流动传导率随压力降低而降低；同时，滑脱效应逐渐增强，吸附气解吸附增大了有效孔隙半径，因而，在压力降低后期，滑脱流动传导率降低幅度逐渐变缓。滑脱流动传导率随孔隙半径增大而增大（图4-a）。随着压力降低，努森扩散权重系数增大，努森扩散传导率增大。努森扩散传导率随孔隙半径增大而增大（图4-b）。表面扩散传导率随压力降低而增大，在低压处却急剧降低。这是由于低压时，吸附气解吸速率大，吸附气浓度急剧降低造成的。表面扩散传导率随孔隙半径减小而增大，这是由于相同孔隙度条件下，孔隙半径越小，表面扩散截面积占气体传输总截面积的份额越大（图4-c）。当孔隙半径大于等于10 nm，气体传输主要受滑脱流动控制，总传导率随压力降低而减小；当孔隙半径小于10 nm，气体传输以表面扩散为主，总传导率随压力降低而增大，在低压处减小（图4-d）。

图5也表明，当孔隙半径大于等于10 nm，以滑脱流动为主，在低压处，滑脱流动和努森扩散对气体传输贡献此消彼长；当孔隙半径小于10 nm，以表面扩散为主，在高压处，表面扩散与滑脱流动相互制约，在低压处，表面扩散与努森扩散相互制约。图5还表明，当孔隙半径小于10 nm，压力50 MPa降低初期，应力敏感显著，造成滑脱流动传输份额减小，努森扩散和表面扩散的传输份额增大。表明由于应力敏感效应，滑脱流动传输量下降幅度最大，努森扩散和表面扩散传输量下降幅度较小；滑脱流动应力敏感强，努森扩散和表面扩散应力敏感弱。

4.2 真实气体效应

页岩纳米孔高压条件下，气体分子之间相互作用力和气体分子自身体积对气体行为的影响不可忽略，用理想气体代替，将造成偏差。与理想气体相比，真实气体分子自由程更大，且随压力增大而增大；与理想气体相比，真实气体吸附能力弱，且随压力增大而差异更大。

真实气体效应影响气体分子自由程与吸附能力，进而影响气体传输能力。当孔隙半径小于10 nm，真实气体效应主要通过分子自由程的增加，从而增加了气体滑脱流动的传输能力，增加幅度随压力增大先增大后减小，且增加幅度随孔隙半径的减小而增大。在低压条件下，压力增大，气体吸附显著，降低有效孔隙半径，加剧了真实气体效应的影响。在高压条件下，压力增大，气体吸附减弱，应力敏感效应显著，增加有效孔隙半径，减弱了真实气体效应的影响；当孔隙半径大于等于10 nm，真实气体效应逐渐减弱了气体滑脱流动的传输能力，这是由于分子自由程增加而增加的传输能力很弱，而气体分子间斥力降低了传输能力，且起主要作用，这种作用随压力增大而增强（图6-a）。真实气体效应增加努森扩散传输能力，并随压力增大而增强，还随孔隙半径增大而增大（图6-b）。真实气体效应通过降低气体吸附能力和覆盖度，从而降低了吸附气表面扩散的传输能力，并随压力增大，降低幅度变得更大（图6-c）。当孔隙半径大于等于10 nm，由于气体传输是以滑脱流动为主，因而真实气体效应对总传输能力影响与对滑脱流动影响类似，大部分压力区间是降低了总传输能力；当孔隙半径小于10 nm，以表面扩散为主，在高压条件下，滑脱流动贡献也较大，因而真实气体效应对总传输能力影响的趋势是表面扩散和滑脱流动综合作用的结果，总体表现为总传输能力降低（图6-d） 。因此，页岩气开发中，是否考虑真实气体效应，对生产动态分析、产能预测和生产制度制订具有显著影响。

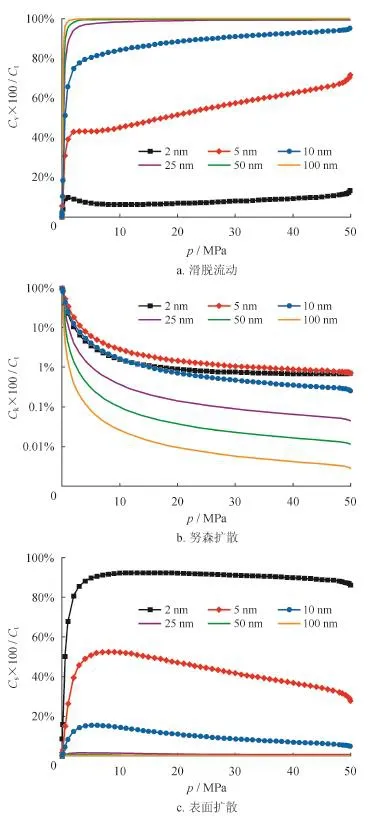
图5 不同传输机理传输份额随压力变化曲线图

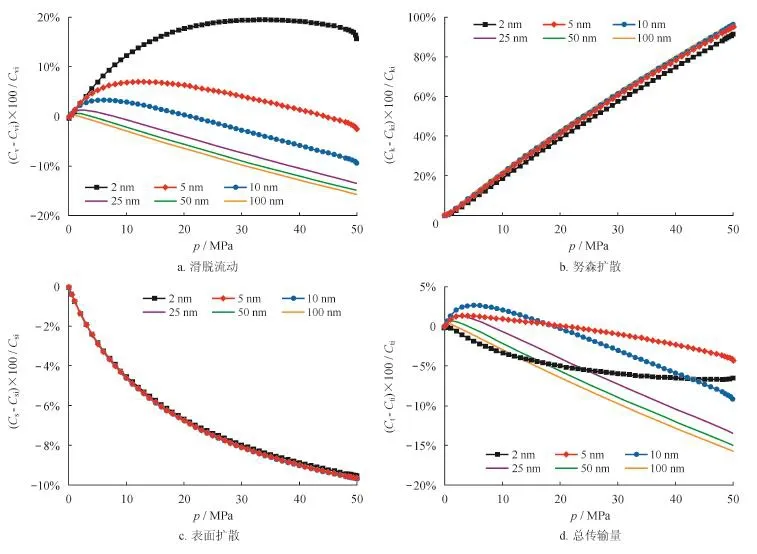
图6 真实气体效应对不同传输机理影响图

4.3 吸附层

随着压力增大，页岩吸附气量增多，吸附层厚度增大，纳米孔体相气体传输的有效孔隙度和有效半径减小，压力增大初期，由于气体吸附显著，减小幅度很大。

页岩吸附气的存在，降低了体相气体传输能力。压力越大，吸附层厚度越大，纳米尺度越小，吸附层截面积占纳米孔截面积的份额越大。所以，吸附层对滑脱流动和努森扩散传输能力的影响随压力增大而增大，随纳米孔尺度减小而增大（图7-a、b）。是否考虑吸附气的存在，对纳米孔气体总传输能力具有显著的影响。当孔隙半径小于10 nm，以表面扩散为主，与不考虑吸附气的表面扩散相比，考虑后的体相气体传输能力虽然下降，但表面扩散却显著增加气体总传输能力；当孔隙半径等于10 nm，在高压处，以滑脱流动为主，表面扩散可忽略，因而降低了气体总传输能力，在低压处，表面扩散贡献大，因而增加了气体总传输能力；当孔隙半径大于等于25 nm，滑脱流动占主导地位，表面扩散可忽略，因而降低了气体总传输能力，且降低幅度随孔隙半径的增大而增大（图7-c）。因此，页岩气藏开发中，是否考虑吸附层和表面扩散，对生产动态分析、产能预测和生产制度制订等具有显著影响，也表明常规油气藏开发理论和方法不能应用于页岩气藏。

4.4 应力敏感效应

页岩气降压开发，有机质纳米孔发生应力敏感，具体表现为有机质孔隙度、渗透率及纳米孔半径随压力降低而降低，在压力降低初期，尤为显著。

图7 吸附层对不同传输机理影响图

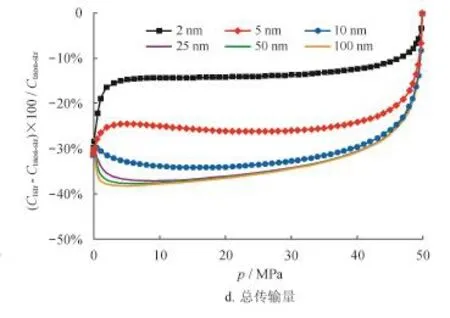
图8 应力敏感效应对不同传输机理影响图

由于应力敏感效应，滑脱流动传输能力随压力降低而降低。在高压条件下，纳米孔尺度越小，应力敏感越强；在低压条件下，由于吸附气解吸附显著，增加纳米孔有效半径，部分抵消了应力敏感效应，应力敏感效应与纳米孔尺度不再是单调关系（图8-a）。同样的，努森扩散和表面扩散也受应力敏感效应的影响，其传输能力随压力降低而降低，且降低幅度随纳米孔尺度的减小而增大（图8-b、c）。总体而言，不管是滑脱流动、努森扩散还是表面扩散，其应力敏感程度随压力降低而增强，随纳米孔尺度减小而增强。然而，纳米孔气体总传输能力应力敏感效应的变化规律却不同，当孔隙半径为2 nm时，以表面扩散为主，在低压处，努森扩散也不可忽略，因此，其应力敏感效应变化规律主要受表面扩散与努森扩散的控制；当孔隙半径为5 nm时，以表面扩散和滑脱流动为主，因而，其应力敏感效应变化规律主要受表面扩散与滑脱流动的控制；当孔隙半径大于等于10 nm时，以滑脱流动为主，因而，其应力敏感效应变化规律主要受滑脱流动的控制。由于滑脱流动应力敏感效应最强，其次为努森扩散，表面扩散最弱。所以纳米孔气体总传输能力的应力敏感效应随纳米尺度减小反而减弱（图8-d），这与常规油气藏应力敏感效应随孔隙尺度减小而增强的变化规律具有本质的区别。因此，应力敏感强的常规油气藏生产动态分析，产能预测和生产制度制订等开发理论和方法不能应用于页岩气藏。

4.5 影响因素主次分析

真实气体效应通过增加气体分子自由程而增大滑脱流动和努森扩散，通过减弱气体吸附能力而降低表面扩散，同时还通过增大气体分子之间斥力而降低滑脱流动。本算例中，不考虑真实气体效应将高估气体总传输能力，最高可达18.65%。应力敏感效应通过降低纳米孔尺度而降低气体总传输能力，不考虑应力敏感效应将高估气体总传输能力，最高可达61.94%；吸附层通过降低体相气体传输的有效半径来降低体相气体传输能力，通过吸附气表面扩散增加气体传输能力。当气体传输以表面扩散为主时，不考虑吸附气，将低估气体总传输能力，最高可达-87.87%；当气体传输以滑脱流动和努森扩散为主，不考虑吸附气，将高估气体总传输能力，最高可达8.51%。当孔隙半径为2 nm时，吸附层对气体传输影响最大，其次应力敏感效应，真实气体效应最弱；当孔隙半径为5 nm时，吸附层和应力敏感效应对气体传输的影响相当，真实气体效应最弱；当孔隙半径大于等于10 nm时，应力敏感效应对气体传输影响最大，真实气体效应和吸附层的影响较弱（图9）。

5 结论

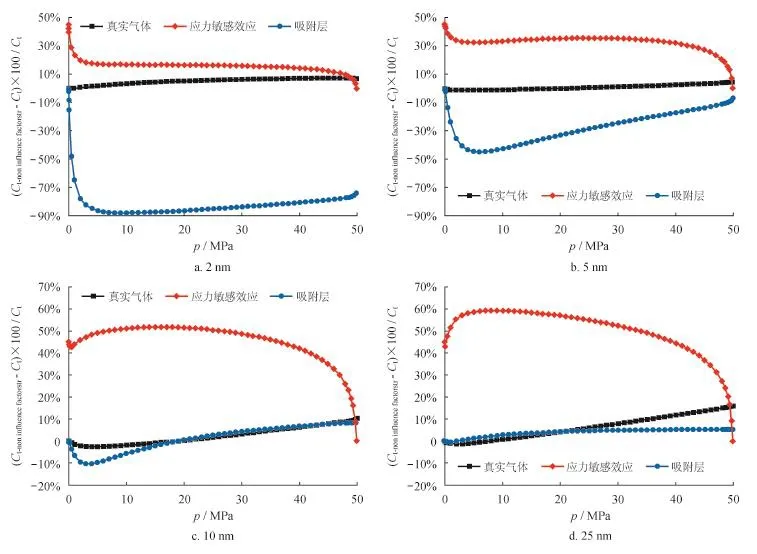
图9 不同纳米孔尺度下不同影响因素对总传输量的影响图

笔者提出了页岩有机质纳米孔气体传输模型，能够描述纳米孔体相气体传输和壁面吸附气表面扩散，同时考虑了真实气体效应、吸附层、应力敏感等微尺度效应的影响。用分子模拟数据验证了体相气体传输模型，用实验数据验证了壁面吸附气表面扩散模型，从而间接验证了综合模型。该模型不仅适用于室内实验条件页岩岩心气体传输，还能推广到强应力敏感页岩储集层高压条件下的气体传输。通过研究，可得出以下结论：

1）分别以气体分子之间碰撞频率和气体分子与壁面碰撞频率占总碰撞频率的比值作为滑脱流动和努森扩散的权重系数，加权建立的页岩有机质纳米孔体相气体传输模型能够合理描述体相气体已知所有传输机理，包括连续流动、滑脱流动和过渡流动。

2）真实气体效应通过增加气体分子自由程而增大滑脱流动和努森扩散，通过减弱气体吸附能力而降低表面扩散，同时还通过增大气体分子之间斥力而降低滑脱流动。

3）基于Hwang模型，通过考虑吸附气覆盖度影响建立了壁面吸附气表面扩散模型。该模型适用于全压力范围。研究结果表明，表面扩散是页岩有机质气体重要的传输机理，当纳米孔尺度很小时，表面扩散主宰了气体传输。

4）页岩气应力敏感效应对气体传输的影响规律不同于常规油气藏：①页岩气与常规油气藏相比，应力敏感效应更强；②常规油气藏应力敏感效应随孔隙尺度减小而增强，而页岩气应力敏感效应随孔隙尺度减小而减弱；③页岩气应力敏感效应对气体传输影响不仅与页岩力学性质和有效应力有关，还与气体传输机理有关。

5）综合考虑真实气体效应、吸附层和应力敏感等微尺度效应耦合作用对气体传输的影响。应力敏感效应和吸附层加剧了真实气体效应对气体传输的影响；是否综合考虑微尺度效应的影响，对页岩气生产动态分析、产能预测和生产制度制订具有显著影响。

本研究未考虑页岩有机质纳米孔迂曲度应力敏感效应和有机质收缩诱导应力变化对应力敏感效应的影响，需进一步研究。还需开展的研究有：考虑限域效应影响的页岩纳米孔气体状态方程[51]；分别考虑页岩有机质纳米孔气体传输模型、无机质纳米孔气体传输模型和微裂缝气体传输模型[8]；同时考虑有机质纳米孔、无机质纳米孔和微裂缝截面形状及尺度分布对气体传输的影响[21]。本研究对于我国埋藏深、有机碳含量和热成熟度高的页岩气开发来说，真实气体、吸附层和应力敏感等微尺度效应的影响更显著，更需要考虑。

[1] 安晓璇, 黄文辉, 刘思宇, 江怀友. 页岩气资源分布、开发现状及展望[J]. 资源与产业, 2010, 12(2): 103-109. An Xiaoxuan, Huang Wenhui, Liu Siyu, Jiang Huaiyou. The distribution, development and expectation of shale gas resources[J]. Resources & Industries, 2010, 12(2): 103-109.

[2] 吴馨, 任志勇, 王勇, 刘长海, 李洋冰, 赵都菁, 等. 世界页岩气勘探开发现状[J]. 资源与产业, 2013, 15(5): 61-67. Wu Xin, Ren Zhiyong, Wang Yong, Liu Zhanghai, Li Yangbing, Zhao Dujing, et al. Situation of world shale gas exploration and development [J]. Resources & Industries, 2013, 15(5): 61-67.

[3] 邹才能, 董大忠, 杨桦, 王玉满, 黄金亮, 王淑芳, 等. 中国页岩气形成条件及勘探实践[J]. 天然气工业, 2011, 31(12): 26-39. Zou Caineng, Dong Dazhong, Yang Hua, Wang Yuman, Huang Jinliang, Wang Shufang, et al. Conditions of shale gas accumulation and exploration practices in China[J]. Natural Gas Industry, 2011, 31(12): 26-39.

[4] 吴克柳, 陈掌星. 页岩气纳米孔气体传输综述[J]. 石油科学通报, 2016, 1(1): 91-127. Wu Keliu, Chen Zhangxing. Review of gas transport in nanopores in shale gas reservoirs[J]. Petroleum Science Bulletin, 2016, 1(1): 91-127.

[5] 吴克柳, 李相方, 陈掌星, 李俊键, 胡源, 姜亮亮. 页岩气和致密砂岩气藏微裂缝气体传输特性[J]. 力学学报, 2015, 47(6): 955-964. Wu Keliu, Li Xiangfang, Chen Zhangxing, Li Junjian, Hu Yuan, Jiang Liangliang. Gas transport behavior through micro fractures of shale and tight gas reservoirs[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(6): 955-964.

[6] 吴克柳, 李相方, 陈掌星. 页岩气纳米孔气体传输模型[J]. 石油学报, 2015, 36(7): 837-848. Wu Keliu, Li Xiangfang, Chen Zhangxing. A model for gas transport through nanopores of shale gas reservoirs[J]. Acta Petrolei Sinica, 2015, 36(7): 837-848.

[7] Wu Keliu, Li Xiangfang, Wang Chenchen, Yu Wei, Chen Zhangxing. Model for surface diffusion of adsorbed gas in nanopores of shale gas reservoirs[J]. Industrial & Engineering Chemistry Research, 2015, 54(12): 3225-3236.

[8] Wu Keliu, Li Xiangfang, Wang Chenchen, Chen Zhangxing, Yu Wei. A model for gas transport in microfractures of shale and tight gas reservoirs[J]. AIChE Journal, 2015, 61(6): 2079-2088.

[9] Wu Keliu, Li Xiangfang, Guo Chaohua, Wang Chenchen, Chen Zhangxing. A unified model for gas transfer in nanopores of shale gas-reservoirs: Coupling pore diffusion and surface diffusion[J]. SPE Journal, 2016, 21(5): 1583-1611. DOI: http://dx.doi. org/10.2118/2014-1921039-PA.

[10] Wu Keliu, Chen Zhangxing, Li Xiangfang. Real gas transport through nanopores of varying cross-section type and shape in shale gas reservoirs[J]. Chemical Engineering Journal, 2015, 281: 813-825.

[11] 赵金洲, 李志强, 胡永全, 任岚. 考虑页岩储层微观渗流的压裂产能数值模拟[J]. 天然气工业, 2015, 35(6): 53-58. Zhao Jinzhou, Li Zhiqiang, Hu Yongquan, Ren Lan. Numericalsimulation of productivity after fracturing with consideration to micro-seepage in shale reservoirs[J]. Natural Gas Industry, 2015, 35(6): 53-58.

[12] Wu Keliu, Li Xiangfang, Wang Chenchen, Yu Wei, Guo Chaohua, Ji Dongqi, et al. Apparent permeability for gas flow in shale reservoirs coupling effects of gas diffusion and desorption [C]//Unconventional Resources Technology Conference, 25-27 August 2014, Denver, Colorado, USA. DOI: http://dx.doi.org/10.15530/ urtec-2014-1921039.

[13] Curtis JB. Fractured shale-gas systems[J]. AAPG Bulletin, 2002, 86(11): 1921-1938.

[14] 王兰生, 廖仕孟, 陈更生, 郭贵安, 吕宗刚, 付永强. 中国页岩气勘探开发面临的问题与对策[J]. 天然气工业, 2011, 31(12): 119-122. Wang Lansheng, Liao Shimeng, Chen Gengsheng, Guo Gui'an, Lü Zonggang, Fu Yongqiang. Bottlenecks and countermeasures in shale gas exploration and development of China[J]. Natural Gas Industry, 2011, 31(12): 119-122.

[15] 吴克柳, 李相方, Chen Zhangxing. 页岩气纳米孔真实气体传输模型[J]. 中国科学: 技术科学, 2016, 46(1): 68-78. Wu Keliu, Li Xiangfang, Chen Zhangxing. Real gas transport through nanopores of shale gas reservoirgs[J]. Scientia Sinica Technologica, 2016, 46(1): 68-78.

[16] Klinkenberg LJ. The permeability of porous media to liquids and gases[C]//API-41-200, Drilling and Production Practice. New York: American Petroleum Institute, 1941: 200-213.

[17] Mason EA, Malinauskas AP, Evans III RB. Flow and diffusion of gases in porous media[J]. The Journal of Chemical Physics, 1967, 46(8): 3199-3216.

[18] Beskok A, Karniadakis GE. Report: A model for flows in channels, pipes, and ducts at micro and nano scales[J]. Microscale Thermophysical Engineering, 1999, 3(1): 43-77.

[19] Javadpour F. Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone)[J]. Journal of Canadian Petroleum Technology, 2009, 48(8): 16-21.

[20] Anderson JM, Moorman MW, Brown JR, Hochrein JM, Thornberg SM, Achyuthan KE, et al. Isothermal mass flow measurements in microfabricated rectangular channels over a very wide knudsen range[J]. Journal of Micromechanics and Microengineering, 2014, 24(5): 308-314.

[21] 吴克柳, 李相方, 陈掌星, 李靖, 梁羽丰, 吴修华. 页岩气复杂孔裂隙真实气体传输机理和数学模型[J]. 中国科学: 技术科学, 2016, 46(8): 851-863. Wu Keliu, Li Xiangfang, Chen Zhangxing, Li Jing, Liang Yufeng, Wu Xiuhua. Real gas transport mechanism and mathematical model through complex nanopores and microfractures in shale gas reservoirs[J]. Scientia Sinica Technologica, 2016, 46(8): 851-863.

[22] 吴克柳, 李相方, 陈掌星. 页岩纳米孔吸附气表面扩散机理和数学模型[J]. 中国科学: 技术科学, 2015, 45(5): 525-540. Wu Keliu, Li Xiangfang, Chen Zhangxing. The mechanism and mathematical model for the adsorbed gas surface diffusion in nanopores of shale gas reservoirs[J]. Scientia Sinica Technologica, 2015, 45(5): 525-540.

[23] Yi Jun, Akkutlu IY, Karacan CÖ, Clarkson CR. Gas sorption and transport in coals: A poroelastic medium approach[J]. International Journal of Coal Geology, 2009, 77(1-2): 137-144.

[24] Clarkson CR, Solano N, Bustin RM, Bustin AMM, Chalmers GRL, He L, et al. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion[J]. Fuel, 2013, 103(1): 606-616.

[25] 苏玉亮, 盛广龙, 王文东, 闫怡, 张璇. 页岩气藏多重介质耦合流动模型[J]. 天然气工业, 2016, 36(2): 52-59. Su Yuliang, Sheng Guanglong, Wang Wendong, Yan Yi, Zhang Xuan. A multi-media coupling flow model for shale gas reservoirs[J]. Natural Gas Industry, 2016, 36(2): 52-59.

[26] Xiong Xinya, Devegowda D, Villazon GGM, Sigal RF, Civan F. A fully-coupled free and adsorptive phase transport model for shale gas reservoirs including non-Darcy flow effects[C]// SPE Annual Technical Conference and Exhibition, 8-10 October 2012, San Antonio, Texas, USA. 2012. DOI: http://dx.doi. org/10.2118/159758-MS.

[27] Fathi E, Akkutlu IY. Multi-component gas transport and adsorption effects during CO2injection and enhanced shale gas recovery[J]. International Journal of Coal Geology, 2014, 123(2): 52-61.

[28] Darabi H, Ettehad A, Javadpour F, Sepehrnoori K. Gas flow in ultra-tight shale strata[J]. Journal of Fluid Mechanics, 2012, 710(12): 641-658.

[29] Majumder M, Chopra N, Andrews R, Hinds BJ. Nanoscale hydrodynamics: Enhanced flow in carbon nanotubes[J]. Nature, 2005, 438(7064): 44.

[30] Holt JK, Park HG, Wang Y, Stadermann M, Artyukhin AB, Grigoropoulos CP, et al. Fast mass transport through Sub-2-nanometer carbon nanotubes[J]. Science, 2006, 312(5776): 1034-1037.

[31] Do DD, Wang K. A new model for the description of adsorption kinetics in heterogeneous activated carbon[J]. Carbon, 1998, 36(10): 1539-1554.

[32] Dong JJ, Hsu JY, Wu WJ, Shimamoto T, Hung JH, Yeh EC, et al. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(7): 1141-1157.

[33] McKernan RE, Rutter EH, Mecklenburgh J, Taylor KG, Covey-Crump SJ. Influence of effective pressure on mudstone matrix permeability: implications for shale gas production[C]//SPE/ EAGE European Unconventional Resources Conference and Exhibition, 25-27 February 2014, Vienna, Austria. DOI: http:// dx.doi.org/10.2118/167762-MS.

[34] Mokhtari M, Alqahtani AA, Tutuncu AN, Yin Xiaolong. Stress-dependent permeability anisotropy and wettability of shale resources[C]//Unconventional Resources Technology Conference, 12-14 August 2013, Denver, Colorado, USA. DOI: http: //dx.doi. org/10.1190/URTEC2013-283.

[35] Wu Keliu, Chen Zhangxin, Li Xiangfang, Guo Chaohua, Wei Mingzhen. A model for multiple transport mechanisms through nanopores of shale gas reservoirs with real gas effect-adsorption-mechanic coupling[J]. International Journal of Heat and Mass Transfer, 2016, 93: 408-426.

[36] 薛华庆, 王红岩, 刘洪林, 闫刚, 郭伟, 李小龙. 页岩吸附性能及孔隙结构特征——以四川盆地龙马溪组页岩为例[J]. 石油学报, 2013, 34(5): 826-832. Xue Huaqing, Wang Hongyan, Liu Honglin, Yan Gang, Guo Wei, Li Xiaolong. Adsorption capability and aperture distribution characteristics of shales: Taking the Longmaxi Formation shale of Sichuan Basin as an example[J]. Acta Petrolei Sinica, 2013, 34(5): 826-832.

[37] 侯宇光, 何生, 易积正, 张柏桥, 陈学辉, 王亿, 等. 页岩孔隙结构对甲烷吸附能力的影响[J]. 石油勘探与开发, 2014, 41(2): 248-256. Hou Yuguang, He Sheng, Yi Jizheng, Zhang Baiqiao, Chen Xuehui, Wang Yi, et al. Effect of pore structure on methane sorption capacity of shales[J]. Petroleum Exploration and Development, 2014, 41(2): 248-256.

[38] Tan Jingqiang, Horsfield B, Fink R, Krooss B, Schulz HM, Rybacki E, et al. Shale gas potential of the major marine shale formations in the Upper Yangtze Platform, South China, Part III: Mineralogical, lithofacial, petrophysical, and rock mechanical properties[J]. Energy & Fuels, 2014, 28(4): 2322-2342.

[39] Civan F, Devegowda D, Sigal RF. Critical evaluation and improvement of methods for determination of matrix permeability of shale[C]//SPE Annual Technical Conference and Exhibition, 30 September-2 October 2013, New Orleans, Louisiana, USA. DOI: http://dx.doi.org/10.2118/166473-MS.

[40] Cui X, Bustin AMM, Bustin RM. Measurements of gas permeability and diffusivity of tight reservoir rocks: different approaches and their applications[J]. Geofluids, 2009, 9(3): 208-223.

[41] Hwang ST, Kammermeyer K. Surface diffusion in microporous media[J]. The Canadian Journal of Chemical Engineering, 1966, 44(2): 82-89.

[42] 郭亮, 彭晓峰, 吴占松. 甲烷在成型纳米活性炭中的吸附动力学特性[J]. 化工学报, 2008, 59(11): 2726-2732. Guo Liang, Peng Xiaofeng, Wu Zhansong. Dynamical characteristics of methane adsorption on monolith nanometer activated carbon[J]. Journal of Chemical Industry and Engineering (China), 2008, 59(11): 2726-2732.

[43] Chen YD, Yang RT. Concentration dependence of surface diffusion and Zeolitic diffusion[J]. AIChE Journal, 1991, 37(10): 1579-1582.

[44] Medved I, Černý R. Surface diffusion in porous media: a critical review[J]. Microporous and Mesoporous Materials, 2011, 142(2-3): 405-422.

[45] Gao Xuechao, da Costa JCD, Bhatia SK. The transport of gases in a supported mesoporous silica membrane[J]. Journal of Membrane Science, 2013, 438: 90-104.

[46] Loyalka SK, Hamoodi SA. Poiseuille flow of a rarefied gas in a cylindrical tube: solution of linearized Boltzmann equation[J]. Physics of Fluids A, 1990, 2(11): 2061-2065.

[47] Wang Moran, Li Zhixin. Micro-and nanoscale non-ideal gas Poiseuille flows in a consistent Boltzmann algorithm model[J]. Journal of Micromechanics and Microengineering, 2004, 14(7): 1057-1063.

[48] Gilliland ER, Baddour RF, Perkinson GP, Sladek KJ. Diffusion on surfaces. I. effect of concentration on the diffusivity of physically adsorbed gases[J]. Industrial & Engineering Chemistry Research, 1974, 13(2): 95-100.

[49] Yeh YT. Diffusion and adsorption of gases in molecular sieves[D]. Buffalo: State University of New York, 1989.

[50] Ruthven DM, Loughlin KF. Correlation and interpretation of Zeolitic diffusion coefficients[J]. Transactions of the Faraday Society, 1971, 67: 1661-1671.

[51] Wu Keliu, Chen Zhangxin, Li Xiangfang, Dong Xiaohu. Methane storage in nanoporous material at supercritical temperature over a wide range of pressures[J]. Scientific Reports, 2016, 6: 33461. DOI: http://dx.doi.org/10.1038/srep33461.

国内储气调峰价格市场化机制起效

2016年11月17日，中国石油华北天然气销售公司在上海石油天然气交易中心(以下简称交易中心)完成首次冬季天然气保供线上交易，这标志着中石油作为国内最大的天然气供应商迈出了利用市场化手段解决冬季调峰供应的第一步。此外，交易中心相关负责人还透露，交易中心正与中石油积极协商明年夏季交易价格下浮的相关事宜。

2016年11月17、18日两天，中国石油华北天然气销售公司共在交易中心完成两笔保供交易，总挂卖量为2 700×104m3，最终成交1 210×104m3。其中，天津滨达燃气实业有限公司17日成交210×104m3，津燃华润燃气有限公司18日成交1 000×104m3。两笔交易的交收时间分别为11月21日至27日、11月21日至25日，交收地点为天津，成交价均为2.3元/ m3，与国家规定的天津市非居民用气基准门站价格相比上浮15%。

今年冬季保供期间，中石油将定期在交易中心平台挂出一部分可调配气量，由市场用户根据需求摘牌。中石油承诺，凡是通过上海石油天然气交易中心平台摘牌得到的天然气，将坚持“先摘先得，保证送到”的原则，确保交易合同的严肃性。同时，对于冬季用气高峰实现价格上浮的用户，在夏季用气淡季，用气价格将给予下浮，以促进天然气销售。2016年夏季，中石油已经在部分地区进行了降价促销，降幅在介于0.1～0.4元/ m3。

业内专家表示，随着冬、夏用气价差的出现，对于储气设施而言，“夏季低价购气、冬季高价售气”的盈利模式变得可行，这将大大有利于实现其经济效益，由市场形成储气、调峰价格的机制正在发挥作用。

（天工 摘编中国石化新闻网）

Micro-scale effects of gas transport in organic nanopores of shale gas reservoirs

Wu Keliu1,2, Li Xiangfang1, Chen Zhangxing1,2
(1. Department of Chemical and Petroleum Engineering, University of Calgary, Calgary, Alberta T2N1N4, Canada; 2. MOE Key Laboratory of Petroleum Engineering//China University of Petroleum, Beijing 102249, China)

The organic pores in shale gas reservoirs are mostly of nanometer scale and the shale gas exists in multiple patterns, so multiple gas transport mechanisms coexist in organic nanopores of shale gas reservoirs. At present, it is in urgent need to figure out the way to establish a nanopore bulk phase gas transport model which can be used to describe all transport mechanisms under high pressure, to describe the surface diffusion in organic nanopores of shale gas reservoirs and to determine the contribution of the surface diffusion to gas transport. In this paper, a model for gas transport in organic nanopores of shale gas reservoirs was built by analyzing comprehensively the micro-scale effects of bulk phase gas transport, surface diffusion, real gas, and adsorption layer and stress sensitivity. Results show that the bulk phase gas transport model which was established based on the weighted superposition of slip flow and Knudsen diffusion can reasonably describe the bulk phase gas transport process; surface diffusion is an important transfer mechanism, and especially in nanopores, and it dominates the gas transport; and the stress sensitivity effect of shale gas reservoirs is different from that of conventional oil and gas reservoirs, and it is related to the organic mechanical properties and the effective stress, as well as the gas transport mechanisms. The model can be extended directly from indoor low-pressure conditions to high-pressure shale reservoirs. It provides a guidance for shale gas production performance analysis, productivity prediction and production system preparation.

Shale gas; Organic pore; Nanopore; Micro-scale; Slip flow; Knudsen diffusion; Surface diffusion; Stress sensitivity

10.3787/j.issn.1000-0976.2016.11.007

2016-08-01 编 辑 韩晓渝）

吴克柳等. 页岩气有机质纳米孔气体传输微尺度效应. 天然气工业，2016, 36(11): 51-64.

NATUR. GAS IND. VOLUME 36, ISSUE 11, pp.51-64, 11/25/2016. (ISSN 1000-0976; In Chinese)

国家自然科学基金项目“页岩油气多尺度渗流特征与开采理论”（编号：51490654） 、国家自然科学基金项目“各向异性裂缝页岩气藏渗流机理与理论研究”(编号：51374222) 、国家重大科技专项“西非深水油田注采参数优化及单井产能预测研究”（编号：2011ZX05030-005-04）。

吴克柳，1985年生，副研究员，博士；主要从事非常规油气开发研究工作。地址：（T2N1N4）2500 University Dr NW, Calgary, AB, Canada。电话：（403）9663673。ORCID: 0000-0002-0021-5007。E-mail: wukeliu19850109@163.com