基于有限元和实验的永磁同步电主轴模态分析

于慎波，王玮琦，钟双双，赵海宁，骆开军

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)



基于有限元和实验的永磁同步电主轴模态分析

于慎波，王玮琦，钟双双，赵海宁，骆开军

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

振动和噪声是评价永磁同步电主轴运行平稳性的一个重要指标，避免电磁力与定子共振是电主轴动态设计过程中必须要考虑的因素。因此较准确地确定定子的固有频率就显得尤为重要。本文对一台功率为9.5 kW的永磁同步电主轴的模态进行了有限元计算和实验测试。通过对各部件进行等效简化，建立了有限元仿真模型。其中对绕组进行两种方式的处理：一是建立简化模型；二是将其质量进行等效处理。之后对电主轴定子结构和整机装配体电主轴单元的模态分别进行了有限元计算。最后借助丹麦B&K振动声学测试系统对电主轴进行实验模态分析，验证计算结果的准确性。

永磁同步电主轴；模态分析；有限元法；B&K测试系统

0 前言

永磁同步电主轴广泛应用于数控机床工业领域中。振动是永磁同步电主轴在工作状态下的一个主要问题，其不但影响轴承和转子等旋转部件的使用寿命，也直接影响电主轴的加工精度。许多文献都将电主轴的电磁力作为振动源进行研究[1-3]。而永磁同步电主轴在工作状态下由电磁力激发产生共振频率时，振动幅值会不断增加，甚至导致电主轴损坏。因此，除了研究电磁力等振动源外，衡量永磁同步电主轴的设计品质也要从其机械性能去判断，模态分析就是对电主轴结构是否发生共振进行预估的重要手段。

从机械的角度来讲，当各部件或者整机工作时的激振频率达到其固有频率时电主轴最容易发生共振[4]。确定结构的固有频率常用的方法有有限元分析法和实验测定法。文献[5]提出了使用实验测定一台两相感应电机模态的方法。对转子进行建模，定义轴的材料属性为钢并且定义硅钢片的阻尼系数。从理论和实验的角度进行模态分析，确定了复杂的装配结构对固有频率的影响。

本文基于有限元分析法和实验测定法，对永磁同步电主轴进行模态分析，较准确地确定了整机的模态。

1 永磁同步电主轴有限元模型

对表面式永磁同步电主轴的机壳、前后端盖、前后轴承、定子铁心、定子绕组、转子铁心、永磁体和主轴等分别进行建模。并对定子机壳绕组和整机进行装配。通过对结构进行有限元模态分析，得到样机的固有频率。为简化分析，本文在建立永磁同步电主轴模态分析模型时做如下了处理：(1)电机各个部件之间紧密配合；(2)略去对固有频率影响甚微的导角和小孔。

绕组结构对整机固有频率的影响一直都是模态分析的一个难点。因为绕组端部的形状复杂，建模的难度大，加之绕组的泊松比、弹性模量等力学参数受槽满率和浸漆工艺影响很大，对其材料参数的设定很难确定。早期的研究都将绕组的质量附加在定子铁心上。之后发现绕组与定子铁心紧密配合对电机固有频率的影响不单单是附加质量作用。M.Benbouzid 等研究指出绕组与铁心紧密配合能明显提高定子结构的固有频率[6-7]。

本文对绕组采用两种处理方法：模型Ⅰ是对绕组进行建模。绕组端部形状复杂，无论是建模还是进行有限元网格划分都很困难，因此需要对其进行合理简化：(1)将绕组端部等效简化为与实际体积相同的圆环；(2)绕组的密度按绕组中环氧树脂、铜线和气隙所占比例等效简化。按照上述方式对永磁同步电机模型进行简化建模，如图1所示。绕组弹性模量参数参考文献[8]。

文献[9]表明在一般的电机结构中，绕组通过绝缘树脂与定子铁心连接，对定子铁心的刚度影响较小，其影响主要以附加质量体现。文献[10]研究了定子铁心，绕组以及绝缘材料三者存在间隙时，采用等效的方法将绕组质量等效到定子齿部计算。模型Ⅱ是将绕组质量附加在定子齿上，增大定子齿的密度，以考虑绕组对固有频率的影响。

图1 永磁同步电机的有限元分析模型Fig.1 FEA model of PMSM

根据样机数据设置材料参数。其中永磁同步电主轴的材料为45号钢，机壳及前后端盖材料为铝。永磁同步电机的有限元分析材料参数见表1。

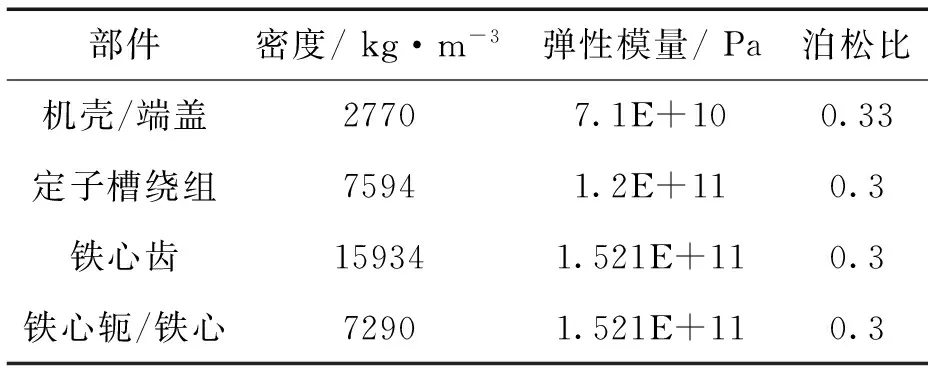
表1 永磁同步电主轴模态有限元分析的材料参数

2 永磁同步电主轴自由模态计算结果

将建立好的永磁同步电主轴有限元模型导入有限元分析软件中，并对各个部件附上相应的材料属性并进行网格划分，最后对其进行无机械约束的自由模态分析。模型Ⅰ为带简化绕组机壳结构、模型Ⅱ为绕组质量等效处理后整机结构，模型Ⅰ和模型Ⅱ的仿真结果分别见表2和表3。

比较定子绕组机壳结构的前四阶模态发现，模型Ⅰ的前两阶模态丢失，3、4阶的固有频率计算误差分别为7.49%和1.86%。模型Ⅱ的前4阶的固有频率计算误差均在5%以内。而比较整机结构的前4阶模态发现，模型Ⅰ的整机装配结构1阶模态丢失，2阶的固有频率计算误差为1.6%，3阶的固有频率计算误差为10.08%，4阶的固有频率计算误差为3.16%。模型Ⅱ的前4阶的固有频率计算误差均在5%以内。由于模型Ⅰ得出的计算结果会丢失部分低阶模态，故之后的分析都按照模型Ⅱ进行。

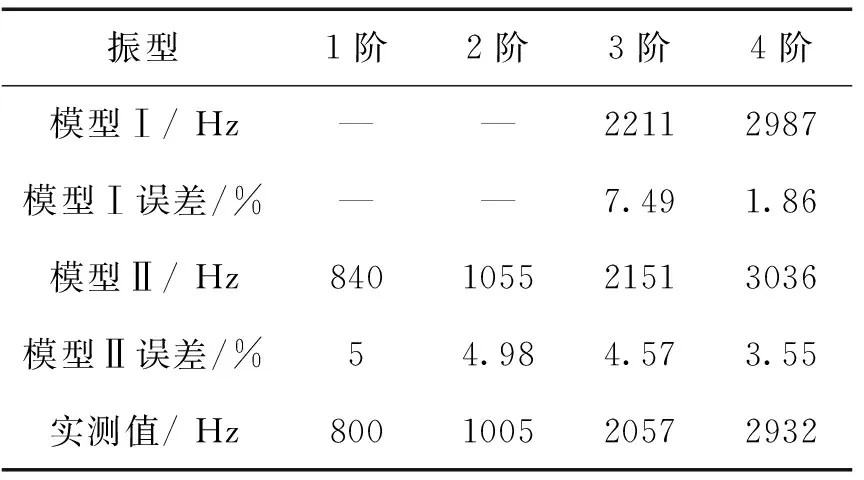
表2 定子机壳计算和测试结果

表3 整机计算和测试结果

各阶模态振型如图2所示，左为绕组定子机壳结构试图，右为整机结构视图。

3 永磁同步电主轴激振器法实验模态分析

为了验证永磁同步电机模态计算的准确性，本文采用丹麦B&K公司振动声学测试系统型号7753模态测试软件对测试样机进行击振器法模态测试。为得到与有限元仿真一致的约束条件，用安全绳将被测样机吊在半空进行测试。图3为模态测试系统示意图。图4为实验现场照片。

图2 各阶模态振型图Fig.2 Modal shapes of each order

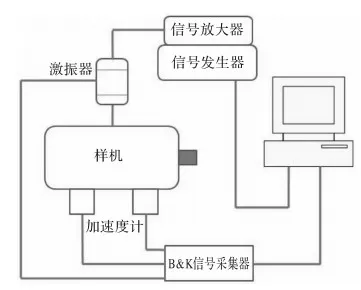
图3 B&K模态测试系统Fig.3 Modal testing system of B&K

图4 实验现场照片Fig.4 Photo of experiment site

首先在B&K PULSE软件中对电机进行建模，并设置激振点和测点。在电机机身设置81个测点，设置发生信号为随机信号，击振100次平均为一步，每步使用3个加速度传感器记录3个测点的信号。之后将加速度计记录的81个频响函数与在PULSE中建立的简化模型一同导入到B&K REFLEX后处理软件中，综合各个测点的频响函数，对电机各阶固有频率进行分析取值。图5为样机某一点频响函数曲线。测试值见表2。

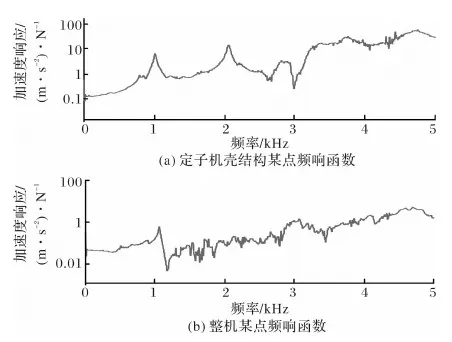
图5 自由状态下样机频响函数Fig.5 Frequency response function of the prototype under free state

4 结论

本文以一台9.5 kW的永磁同步电机为研究对象，建立了样机各个部件的三维模型，对定子机壳结构和整机结构进行了有限元分析计算并进行了试验测定。经分析得出以下结论：

(1)使用绕组等效简化模型进行有限元计算得出的结果，会丢失部分低阶固有频率。

(2)将绕组质量等效处理后进行仿真计算的结果与测试各阶固有频率误差均小于5%，计算结果达到较高的准确度。证实了本文的模态计算分析的准确性和建模方法的优越性。对研究永磁同步电主轴振动噪声提供了重要的参考依据。

[1] N.Feki, G.Clerc, Ph.Velex. An integrated electro-mechanical model of motor-gear units-Applications to tooth fault detection by electric measurements[J]. Mechanical Systems and Signal Processing, 2012,29：377-390.

[2] M.P.Sanchez, M.R.Guasp, J.A.A.Daviu, et al.Panadero. Diagnosis of Induction Motor Faults in the Fractional Fourier Domain[J]. IEEE Trans. on Instrumentation and Measurement, 2010,59(8)：2065-2075.

[3] M.A.Awadallah, M.M.Morcos, Application of AI Tools in Fault Diagnosis of Electrical Machines and Drives-An Overview[J].IEEE Trans. on Energy Conversion, 2003, 18(2)：245-251.

[4] D.J.Ewins, Modal testing: practice and theory[M]. New-York: John Wiley & Sons Inc., 1986.

[5] M.Filip, E. Helerea. Modal Test of an Electrical Machine Rotor[A].International Conference on Optimization of Electrical and Electronic Equipment[C]. Brasov, Romania: IEEE, 2010： 526-531.

[6] Tetsuya H., Katsuyuki N.， Takashi Y． Modeling method of vibration analysis model for permanent magnet motor using finite element analysis[A]. International Conference on Electrical Machines and Systems[C]. Tokyo, Japan：IEEE, 2009：1-6.

[7] Benbouzid M.E.H, Reyne G, Derou S, etal． Finite Element Modeling of a Synchronous Machine： Electromagnetic Forces and Mode Shapes[J]. IEEE Trans on Magnetics, 1993, 29(2)：2014-2018.

[8] Long S.A, Zhu Z.Q, David H. Vibration Behavior of Stators of Switched Reluctance Motors[J]. IEE Proceedings-Electric Power Applications, 2001, 148(3)：257-264.

[9] 孙剑波， 詹琼华， 黄进. 开关磁阻电机的定子振动模态分析[J]. 中国电机工程学报， 2005， 25(22)：148-152.

[10]于慎波， 王辉， 姜菲菲. 电机定子圆柱壳体轴向模态频率计算[J]. 电机与控制学报， 2014， 18(6)：102-107.

Modal analysis of permanent magnet synchronous motorized spindle based on experimental and finite element method

YU Shen-bo, WANG Wei-qi, ZHONG Shuang-shuang, ZHAO Hai-ning LUO Kai-jun

(School of Mechanical Engineering , Shenyang University of Technology, Shenyang 110870, China)

The vibration and noise are an important index appraising stability of running for a permanent magnet synchronous motorized spindle (PMSMS). While, it is a considerable factor that resonances between magnetic forces and stator are avoided in dynamic design of PMSMS. Therefore, it is a vital problem to determine nature frequencies of the stator accurately. This paper presents that the modes of a 9.5 kW PMSMS are investigated by finite element method(FEM) and experimental method. The finite element model is constructed by equivalently simplified each parts. There are two simplified methods about the winding, establishing the winding simplified model, processing winding mass equivalently. The modes of stator with frame and whole assembly spindle units are calculated by using FEM, respectively. Finally, the experimental modal analysis of PMSMS is completed by Denmark B&K test system of vibration and acoustics. The accuracy of theoretical modal frequency values was validated.

permanent magnet synchronous motorized spindle; modal analysis; finite element method; B&K test system

2015-10-20；

2015-11-23

国家自然科学基金资助项目(51175350)；沈阳市科技计划项目(F15-199-1-13)

于慎波(1958-)，男，辽宁沈阳人，沈阳工业大学机械工程学院教授，博士，研究方向为电机噪声与振动抑制技术、转子系统动力学、噪声与振动控制等领域的研究工作。

王玮琦(1990-)，男，辽宁沈阳人，沈阳工业大学机械工程学院在读硕士，研究领域为电机噪声与振动抑制技术。

TH122

A

1001-196X(2016)05-0068-04