基于改进CGA的配电网重构

王 玮，刘德龙，吴学智，张尚腾

(北京交通大学 国家能源主动配电网技术研发中心，北京 100044)



基于改进CGA的配电网重构

王 玮，刘德龙，吴学智，张尚腾

(北京交通大学 国家能源主动配电网技术研发中心，北京 100044)

针对遗传算法易早熟收敛和易产生大量不可行解的问题，提出了一种基于改进的克隆遗传算法(CGA)的配电网重构方法.该方法对克隆遗传算法进行了3点改进：通过简化网络结构，缩短了算法中染色体的长度；采用基于环路的编码方式，避免了产生大量不可行解；改进克隆遗传算法的选择算子、基因移位和突变操作，克服了早熟收敛的问题，提高了算法的收敛速度.本文以网损最小为优化目标对算例进行了重构，同时与基于遗传算法及粒子群算法的配电网重构进行了比较，算例结果表明：改进的CGA具有较高的寻优性能，应用于配电网中可以起到减小网损的作用.

配电网重构；改进的克隆遗传算法；网损

配电网中存在大量的分段开关和少量联络开关，一般具有闭环设计和开环运行的特点.配电网重构就是通过改变上述开关的运行状态来改变网络拓扑结构，使负荷在网络中发生流动，从而提高配电网的电能质量，如降低网损和调节电压等[1].国内外学者对配电网重构进行了大量研究，目前的算法主要分为：最优流模式法[2]和支路交换法[3]等启发式方法；遗传算法[4]、粒子群算法[5]和蚁群算法[6]等人工智能方法.传统遗传算法(GA)主要通过交叉算子来繁殖后代，应用于配电网重构时通常存在两个问题：易在交叉操作时产生大量的不可行解；当交叉算子不能产生新个体时，遗传迭代就无法进行下去，这就

会出现早熟收敛现象.克隆遗传算法[7]取消了传统遗传算法中的交叉算子，采用基因重组的方法，仅在一条染色体上进行全部遗传操作，这样不仅简化了遗传操作，而且减少了大量不可行解的产生，提高了寻优效率[8].同时该算法不要求初始群体中个体的多样性，因此也不会发生早熟收敛现象.

结合配电网的实际情况，本文作者采用了基于环路的编码方式，并在克隆遗传算法( CGA)的基础上对选择算子、基因移位和突变操作进行了改进，来提高算法的寻优效果.

1 重构的数学模型及约束条件

把网络损耗最小作为重构优化目标，函数式为

(1)

式中：ri为支路i电阻；Pi、Qi分别为支路i末端流过的有功功率、无功功率；Vi为支路i末端节点电压；b为支路数；ki为开关i状态变量，是0-1的离散量，0表示打开，1表示闭合；f为网络损耗.

本文使用前推回代法进行配电网潮流计算，重构时应满足的约束条件如下：

1)节点电压约束

Vi,min≤Vi≤Vi,max

(2)

式中： Vi,max和Vi,min为各节点电压的上限和下限.

2)支路容量约束

Si≤Si,max

(3)

式中：Si,max为第i条支路上的最大容许功率.

使用罚函数将不等式约束条件加入目标函数中

(4)

式中：m为i的取值上界，通常取2；g1(Vi)、g2(Si)分别为节点电压和支路容量的罚函数；P是惩罚因子，通常取7.同时，配电网运行时要求呈辐射状结构且无孤岛.

2 面向配电网重构的改进CGA

2.1 染色体编码方式的改进

配电网重构是通过改变网络中开关的开合状态来改变拓扑结构，找到一个满足寻优目标的最优开关组合.因此把开关状态作为控制量.用0或1表示开关状态一个开关代表染色体的一个基因位，每个开关状态组合起来，就形成了一条染色体，同时为了使所有负荷都能得到供电，要求与电源点相连的开关及不在任何环路内的开关都要闭合.原始配网如图1(a)所示，原始配网如图1(a)所示，图1(a)中节点9不在任何环路内，必须要求有线路连接才能供电，所以8和9之间的开关必须闭合.简化系统如图1(b)所示，图1(b)中将节点9与节点8简化成一个节点简化系统见图1(b).

根据配电网闭环设计的特点，采用染色体分段编码方式，让一个环路内的开关构成一条染色体，则该染色体中只有一个基因位为0，这样能避免不可行解的产生.对于图1(b)中的配电系统，它存在3个环路，其染色体编码结果如表1所示

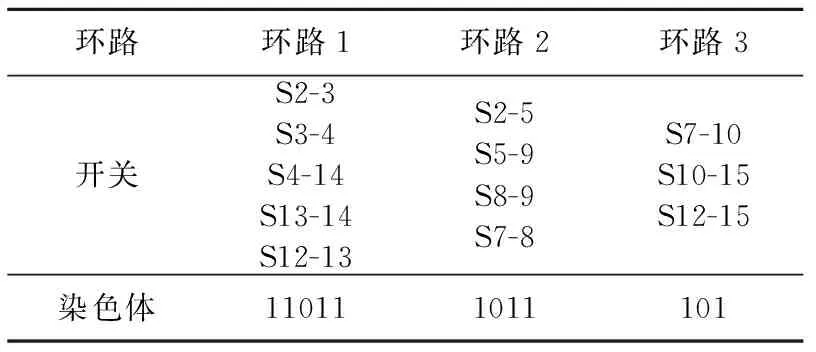
表1 染色体编码情况Tab.1 Chromosome coding situation

表1中以环路3为例，它包含开关S7-10，S10-15，S12-15，这些开关构成了一条染色体，该染色体中只有一个基因位为0，即S10-15是打开的.

2.2 适应度函数

本文改进CGA算法通过潮流计算得到群体中所有个体的适应度值，根据适应度值指导克隆遗传算法进行寻优.CGA算法搜索方向的依据是适应度值，所以适应度值应为正，同时要求目标函数的优化方向必须向着适应度值增加的方向变化.以网络损耗最小为优化目标进行网络重构，属于最小值优化问题.本文把目标函数转换成适应度函数的形式为

F1=1/fmin

(5)

式中：F1为适应度值；fmin为优化目标函数.

2.3 克隆遗传操作

遗传算子作用于当前群体后会产生新的个体，根据选择的进化方向，逐代进行遗传和选择操作，进而实现群体进化，最终得到全局最优解.CGA的遗传算子包括基因重组和突变算子，基因重组算子又包括基因移位、换位和倒位算子，它们有相同的遗传操作功能，基因移位的程序更容易实现，因此本文的基因重组采用移位算子.综上，本文使用基因移位和突变的克隆遗传算法进行重构.

1)选择算子的改进.克隆遗传算法同遗传算法一样使用选择算子对群体中的个体进行选择操作.选择操作建立在对个体适应度值进行评价的基础上，适应度值越高的个体被遗传到下一代的概率越大.为避免CGA 的轮盘赌选择在个体适应度值相差较大时易出现早熟收敛现象，本文采用最优个体保留策略，直接复制到下一代，更新替换本代群体中经基因重组和突变运算后生成的适应度值最低的个体.

2) 改进CGA的基因移位操作.CGA基因移位操作是按一定概率把一条染色体中的某个(或某些)子串的基因依次向后移，同时把最后一位基因移到最前面.在一条染色体中进行基因移位的子串是随机的，采用单点移位操作.

较小移位率有利于局部搜索，较大移位率有利于全局搜索，因此本文在算法初期采用较小移位率，随着算法的进行逐渐加大移位率，这样可以减少局部最优现象的出现；同时对于全局最优个体，由于采用了最优个体保留策略，其并不会受到影响.迭代过程中变化的移位率能避免早熟收敛现象，使算法快速收敛到全局最优解.

3) 改进CGA基因突变操作.CGA基因突变操作是按一定概率改变一条染色体中某个(或某些)位置上的基因值，突变位置是随机选取的.本文采用二进制编码方式，先选定一条染色体，然后随机将其一个基因位取反，这样会产生有2个0或全为1的解，即不可行解.使用如下设定：若突变将1的基因位变为0，就将其后一位突变前为0的基因位变为1；若突变将0的基因位变为1，就将其后一位突变前为1的基因位变为0.这样可以避免不可行解的产生，提高收敛速度.

在CGA中，若突变率取值太大，可能会破坏许多较好模式，若突变率取值太小，抑制早熟收敛和产生新个体的能力又会变差.本文使用最优个体已经保留的迭代数，让突变率随迭代数的变化动态调整.

3 算法步骤和流程图

改进的CGA步骤如下：1)将开关状态转化为染色体编码，并简化编码，让不在环路内及与电源点相连的开关不参与编码；2)确定种群规模，产生初始群体；3)通过潮流计算得到初始群体中各个体的适应度值；4) 采用最优个体保留策略进行选择操作，适应度值最高的个体直接复制到下一代；5)对上一代群体中的个体进行改进的基因移位和突变操作，产生新个体；6)判断收敛准则，满足时输出结果，否则使代数增加，继续从步骤3)迭代.改进的CGA流程如图2所示,图中G表示迭代次数.

4 算例分析

算例采用IEEE 33节点配电系统[9]如图3所示，其中节点1为电源点，额定电压为12.66 kV，总负荷为3 715 kW+j2300 kVar.图3中实线为分段，虚线为联络开关.

图3算例中开关1-2必须闭合，所以染色体的长度为36.

以网损最小为优化目标，使用本文的改进CGA，对配电网进行重构，设定种群规模为50，最大迭代次数为30，初始移位概率为0.9，初始突变概率为0.05.重构结果如表2所示.

遗传算法[10]和粒子群算法[11]用于配电网重构时的降损效果，将本文算法与这两种方法进行比较，比较结果也放在了表2中.由表2可知，利用本文的改进CGA进行重构，能使网损降低40.9%，明显低于经遗传算法重构的25.6%和经粒子群算法重构的30.2%，同时最低节点电压提高幅度为2.5%，高于遗传算法和粒子群算法的1.9%，这就证明了本文算法具有更好的寻优效果.

表2 各算法重构结果Tab.2 Reconstruction results of each algorithm

此外，重构前后网络中各节点电压对比情况如图4所示.由图4可见本文重构不仅可以降低网损，同时能提高网络节点电压，改善供电质量.

迭代过程中，目标函数值的变化情况如图5所示.由图5可知，在进化到7代以后，网损值不再变化，这就说明已经找到了最优解，由此可见本文算法收敛性较好.而遗传算法、粒子群算法收敛到最优解的进化代数分别为21和20，这就说明本文算法具有更好的寻优性能.

5 结语

1)本文作者提出基于改进CGA的配电网重构，保留GA操作简单的特点，同时克服GA易早熟收敛的问题，对初始群体中的个体没有多样性要求.

2)根据配电网闭环设计的特点，采用基于环路的编码方式，并改进了选择算子、基因移位和基因突变操作，避免了不可行解的产生，提高了收敛速度.

3)算例结果表明：使用本文改进CGA的配电网重构能很好地降低网络损耗，抬高网络电压和改善供电质量.与基于遗传算法和粒子群算法的配电网重构方法相比，本文的改进算法寻优效果性能更好.

[1] 王守相，王成山．现代配电系统分析[M]．2版. 北京：高等教育出版社，2014：193． WANG Shouxiang, WANG Chengshan. Modern distribution system analysis[M]. 2nd. ed. Beijing: Higher Education Press,2014：193．(in Chinese)

[2] 韩林林. 智能配电网网络重构方法的研究[D]. 郑州: 郑州大学, 2013. HAN Linlin. Study on network reconfiguration method of smart distribution grid [D]. Zhengzhou :Zhengzhou University,2013. (in Chinese)

[3] CIVANLAR S, GRAINGER J J, YIN H, et al. Distribution feeder reconfiguration of loss reduction[J]. IEEE Transaction on Power Delivery, 1988, 3(3): 1217-1223.

[4] WHITLEY D. A genetic algorithm tutorial[J]. Statistics & Computing, 1994, 4(2):65-85.[5] KENNEDY J, EBERHART R. Particle swarm optimization[C].Proceedings of IEEE International Conference on Neural Networks, 1995: 1942-1948.

[6] 黄烨．一种基于MOGA的含DG配电网络多目标重构方案[J]．自动化与信息工程，2012(2)：8-12． HUANG Ye．A multi-objective reconfiguration formula for DG distribution network based on MOGA[J]．Automation & Information Engineering，2012(2)：8-12．(in Chinese)

[7] 史峰，王辉，郁磊，等．MATLAB智能算法30个案例分析[M]．北京：北京航空航天大学出版社，2011：103-135． SHI Feng, WANG Hui, YU Lei, et al. 30 case studies based on intelligent algorithms MATLAB[M].Beijing: Beihang University Press, 2011 : 103- 135. (in Chinese)

[8] 刘健, 毕海翔, 董海鹏. 复杂配电网简化分析与优化[M]. 北京: 中国电力出版社, 2002: 184. LIU Jian, BI Haixiang, DONG Haipeng. Simplify the analysis and optimization of complex distribution network[M]. Beijing: China Electric Power Press, 2002:184. (in Chinese)

[9] GOSWAMI S K, BASU S K. A new algorithm for the reconfiguration of distribution feeders for loss minimization[J]. IEEE Trans on Power Delivery, 1992, 7(3): 1484-1491.

[10] 黄弦超，杨雨．基于电流分点编码的遗传算法在配电网重构中的应用[J]．电力系统自动化，2013，37(19)：74-79． HUANG Xianchao, YANG Yu．Network reconfiguration in distribution systems based on genetic algorithm with current point coding technique[J]．Automation of Electric Power Systems，2013，37(19)：74-79．(in Chinese)

[11] 田昊, 吕林, 高红均,等. 计及电网运行特性的配电网动态重构[J]. 电力系统保护与控制, 2015, 43(1): 9-14. TIAN Hao, LYU Lin, GAO Hongjun, et al. Dynamic reconfiguration of distribution network considering power grid operation characteristic[J]. Power System Protection and Control, 2015, 43(1): 9-14. (in Chinese)

Distribution network reconfiguration based on improved CGA

WANGWei,LIUDelong，WUXuezhi，ZHANGShangteng

(National Active Distribution Network Technology Research Center, Beijing Jiaotong University, Beijing 100044, China)

Aiming at the problem that the genetic algorithm(GA) is easy to premature convergence and generate a large number of infeasible solutions, this paper proposes a new method of distribution network reconfiguration based on improved clonal genetic algorithm (CGA). It has three improvements: by simplifying the network structure, shorten the length of the chromosomes in the algorithm; the coding method based on the loop, to avoid producing infeasible solutions; improved clonal selection operator of GA, gene translocation and mutation operation, to overcome the problem of premature convergence and improve the convergence speed of the algorithm. In this paper, the optimization of the target is reconstructed, and the distribution network reconfiguration based on GA and particle swarm optimization algorithm are compared. The results show that the improved clonal GA has better optimization performance and it could reduce the network loss in distribution network.

distribution network reconfiguration; improved clonal genetic algorithm; network loss

2015-12-31

国家能源应用技术研究及工程示范项目资助(CNY20150301)

王纬(1959—)，男，辽宁锦州人，教授.研究方向为新能源及新型发电技术.email：wwang2@bjtu.edu.cn.

TM73

A

1673-0291(2016)05-0100-04

10.11860/j.issn.1673-0291.2016.05.017