大规模MIMO系统中的双向搜索天线选择算法
刘 留,迟 盛,刘 凯,陶 成
(北京交通大学 电子信息工程学院,北京 100044)
大规模MIMO系统中的双向搜索天线选择算法
刘 留,迟 盛,刘 凯,陶 成
(北京交通大学 电子信息工程学院,北京 100044)
大规模MIMO(Massive MIMO)拥有众多天线,如果按照传统的方式配备等量的射频链路,势必会大幅度增加硬件成本及系统复杂度.天线选择技术能够在不损害多天线系统优势的前提下,使射频链路成本明显下降.天线选择的主要方法其思想是在全部天线中选出部分天线传输数据,从而使射频链路成本不再成为限制因素,在实际的无线信道中,信道状态变化多样,为了达到所需性能指标,通信系统需要选择不同数目的天线进行数据传输,而现有的天线选择算法往往只适用于固定天线数的场景.本文针对多变的信道状态,基于递增选择算法与递减选择算法提出了双向搜索天线选择算法,能够灵活应对不同的天线数需求,并且保持了较低的计算复杂度.
大规模MIMO系统;天线选择;双向搜索;递增选择;递减选择
多输入多输出(Multiple-Input Multiple-Output, MIMO)技术通过多天线配置带来的多个空间通道传输无线数据流,让空间成为一种可以用于提高性能的资源,能够在不拓展带宽的条件下显著提高系统的数据传输速率;利用多天线实现空分复用,空间分集和波束成型等功能,可以提高信道的容量,增大信道可靠性,改善无线通信系统的性能.通常在无线通信系统的收发两侧配置的天线数目越多,系统可以获得的信道自由度就越大,数据传输就可以拥有更高的有效性和可靠性.但是,由于实际部署的难度及系统复杂度的限制,当前MIMO通信系统中的天线数量还比较少,比如,在LTE标准中最多可以采用八副天线(基站侧).随着人们对无线通信需求的提高,传统MIMO技术已经不能支持日益激增的无线数据需求.因此,2010年底,贝尔实验室在传统MIMO技术的基础上提出了大规模MIMO(Massive MIMO)技术[1].
大规模MIMO将天线数目增加到几十个甚至上百个,能够提供更大的分集增益和复用增益,从而显著提高信道容量和频谱效率[2].在国内外的进一步研究中,大规模MIMO有望成为未来的第5代通信系统的核心技术[3-4],并且有潜力实现未来轨道交通特别是高速铁路的通信需求[5-6].大规模MIMO的接入方式可以分成两大类:点对点(Point to Point)接入和多用户(Multi-user)接入.在点对点接入方式中,大规模MIMO系统的发射与接收两侧都安装有大量天线,不必拓展带宽就能增加频带利用率,为无线通信系统提供高速数据传输.在多用户接入方式中,基站配置大量天线,用户使用配有单天线或者双天线的终端,终端与终端不存在协作关系,通过预编码获得相应的复用增益,本文主要考虑点对点的接入方式.
虽然大规模MIMO系统中天线数目的增加带来了许多优势,但是在实际部署等方面也带来了不少挑战.在实际应用中,通信系统需要为每根天线配置相应的射频链路,包括功率放大器、模数转换器和混频器等,随着天线数目的增多,系统前端射频链路的硬件复杂度、体积和成本会随之增加,加剧了系统配置和维护的难度,同时加重信号处理的负担,这一限制因素在大规模MIMO系统中更加突出.天线选择技术能够在保证系统容量和系统可靠性的条件下,降低系统复杂度与射频成本[7].天线选择技术的思想就是根据相应的准则,从收发两端的所有天线中选取一部分天线,通过这部分天线及相应的射频链路进行无线信号的传输.
追求信道容量最大化与追求系统误码率最小化是天线选择的两个主要准则.最优的天线子集可以通过穷举遍历的方式找到,即计算每个可能的天线子集的信道容量,选取其中信道容量最大的那一个子集,穷举算法是基于信道容量最大化准则的最优算法,但运算量相当大,计算复杂度随天线数的增加呈指数上升,实现难度大,并不具有实用性.研究人员针对MIMO系统的快速天线选择算法进行了广泛的研究.文献[8]中给出了基于范数的快速选择算法,该算法通过找到信道矩阵中欧氏范数最大的前若干行(信道矩阵的行对应MIMO系统中的接收天线),选择出对应的接收天线子集.文献[9]基于信道容量最大化准则,结合贪心算法的思想,提出了近似最优的递减天线选择算法,类似的,文献[10]提出了递增天线选择算法.
上述几种天线选择算法以损失少量性能为成本,使得计算复杂度明显下降,在不同的信道环境和不同的通信系统配置中,有着各自的优势和不足.对于选择天线数较少的情况,递增选择算法更为适用,因为它的计算复杂度较小;对于选择天线数较多的情况,递减选择算法更为适用,由于考虑了剩余天线的整体作用,性能更好,但计算复杂度较大;最大范数算法计算复杂度低,但性能与前两种算法仍有差距.
传统MIMO系统下的天线选择算法不一定适用于大规模MIMO系统,针对大规模MIMO系统,文献[11]设计了适用于60 GHz频段短距离通信的天线选择算法,文献[12]提出了逐个天线迭代的实时发射天线选择算法,性能接近最优算法且具有较低的计算复杂度,文献[13]基于信噪比最大化准则,给出了一种大规模MIMO系统中的天线选择算法,文献[14]结合实际测量的大规模MIMO信道数据,提出了基于功率和基于凸优化的天线选择算法,并对两者的性能进行了比较分析.上述几篇文献从不同角度对大规模MIMO系统中的天线选择算法进行了研究,分别提出了满足各自不同需求的天线选择算法.
在大规模MIMO系统的条件下,针对多变的信道对选择天线数的不同要求,本文作者在递增与递减选择算法的基础上提出了双向搜索算法,综合两者算法的优点,能够在保持较低计算复杂度的前提下,对不同的选择天线数需求有更强的适应能力,有效应对信道状态的变化.
1 大规模MIMO系统模型
在平坦衰落的条件下,一个配备有Ns根发射天线,Nr根接收天线的点对点大规模MIMO系统,信道的输入输出模型可以表示为:
(1)
其中
r(t)=[r1(t),r2(t),…,rNr(t)]T
(2)
s(t)=[s1(t),s2(t),…,sNs(t)]T
(3)
w(t)=[w1(t),w2(t),…,wNr(t)]T
(4)
(5)
式中:r(t)为Nr×1维接收信号向量;s(t)为Ns×1维发射信号向量;w(t)表示均值为0、方差为1的Nr×1维加性高斯噪声向量;[·]T表示矩阵转置;ρ为平均信噪比;H∈Nr×Ns为信道矩阵;N×M定义了所有N×M维复数矩阵构成的向量空间,其中的矩阵元素hij为第j根发射天线到第i根接收天线的衰落系数.
如果发射机不知道瞬时信道状态信息,则发射机需要把发射功率平均分配给所有发射天线.对于给定的信道矩阵H,系统的信道容量可以表示为
(6)
式中:In为n×n维单位矩阵;det(·)表示矩阵的行列式;(·)H表示矩阵共轭转置.
图1为天线选择的示意图,无线通信系统分别在Ns根发射天线中选出Ls根发射天线,在Nr根接收天线中选出Lr根接收天线进行信号发送与接收.
假设在Nr根接收天线中选取Lr根进行信号接收,即Lr (7) 2.1 递减与递增选择算法 由于双向搜索算法是在递减选择算法与递增选择算法的基础上演变而来,为了更好的理解双向搜索算法,下面对递减与递增选择算法进行简单的介绍.递减选择算法与递增选择算法是次优的快速选择算法,利用矩阵求逆引理[15]等相关矩阵知识简化运算,代替穷举遍历.递减选择算法的主要想法是,在接收端的全部Nr根天线中,每次去掉对信道容量损失最小的那一根天线,循环迭代,直到剩余Lr根天线.类似的,如果选择算法从空集开始,每次选择添加一根使系统容量的增量最大的天线,循环迭代,直到选择出Lr根天线,则是递增选择算法,表1列出了递减与递增两种选择算法的具体步骤及相应的计算复杂度,其中:hj(1≤j≤Nr)是信道矩阵H中的第j行;Ω为所有接收天线构成的集合;αj为第j根天线对信道容量的贡献j∈Ω,J为当前循环选择出的天线序号;矩阵a与B是为了计算方便而引入的中间变量;程序的返回值是选择后的天线序号集合;O(·)记号表示算法计算复杂度的上界. 对于不同的选择天线数,两种算法各有优势与不足:1)递增选择算法从空集开始选择,适用于选择天线数较少(Lr≤Nr/2)的情况;2)而递减选择算法从全集开始选择,更适合选择天线数较多(Lr≥Nr/2)的情况.假如在选择天线数较少时采用递减选择算法,则算法循环迭代次数较多,运行时间较长,影响通信系统性能,反之亦然. 文献[16]对上述两种算法分别给出了改进方案,改进的递增选择算法是在原始递增选择算法的基础上,每次循环改为同时处理接收端的两根天线,不仅选出信道容量增量最大的一根天线,而且淘汰信道容量增量最小的一根天线,改进的递减选择算法处理方式与之类似.和单次只处理一根天线相比,计算量最多减少1/3,并且对系统的容量几乎没有影响.由于这两种改进的算法只是单独对递增或者递减选择算法进行改进,虽然能够加快处理速度,但并没有改变单独的递减或递增选择算法主要适用于固定选择天线数的情况.在实际的传播环境中,信道状态千变万化,为了满足相应的系统指标,需要确定不同的选择天线数,并且保持较低的计算复杂度.因此,本文作者在递减与递增选择算法的基础上,采用同时处理两根天线的操作方法,提出了双向搜索天线选择算法. 表1 递减与递增选择算法的具体步骤及相应的复杂度Tab.1 Decremental and incremental selection algorithms and the corresponding complexity 2.2 双向搜索算法 双向搜索选择算法的思想是将递增与递减两种算法结合起来,分别从空集和全集向所需的天线子集搜索逼近,任意一侧达到指定天线数即停止.每次循环迭代中,根据递增选择算法选出容量增益最大的一根天线,并且利用递减算法去掉容量损失最小的一根天线,同时在全集中去掉这两根天线,下次循环从剩余的天线中选择,即循环的待选集合中元素个数每次减少两个.因为每次循环处理两根天线,与单纯的递增或者递减选择算法相比,每一步的计算量会稍微大一些,但是这一种处理方式可以很大程序上减小下一次循环迭代的计算量,能够快速收敛到所需的天线子集.由于算法是从两侧同时逼近,在每次循环中,实际上是选出了一大一小两个天线子集,任意一个达到指定的天线数即完成选择,这一方式能够灵活应对不同的选择天线数需求.下面总结了双向搜索算法的基本步骤. 1)初始化:Ω为所有接收天线构成的集合,Ω={1,2,…,Nr};S为递增选择算法选择出的天线子集,开始赋值为空集S=∅;T为递减选择算法选择出的天线子集,开始赋值为空集T=∅. 2)在集合Ω中,通过递增选择算法找到一根容量增益最大的天线J,加入集合S,同时在集合Ω中去掉J.如果集合S中天线个数满足要求,则退出循环,如果集合S中天线个数不满足要求,则转到步骤3). 3)在集合Ω中,通过递减选择算法找到一根容量损失最小的天线P,从集合Ω中去掉P,并将集合S加上集合Ω赋值给集合T,如果集合T中天线个数满足要求,则跳出循环,否则回到步骤2)继续循环. 4)将集合S或者T中满足所需天线数的一个集合作为程序的返回值Z,完成选择. 由于算法的计算复杂度主要集中在循环中,本文作者利用文献[17]中的改进方法,进一步降低原始递减选择算法循环中的计算复杂度.Hk表示在第k步中,根据递减选择算法获得的信道矩阵,则第k+1步的结果就是在第k步的结果上去除掉矩阵中的相应一行,用rk,j表示,j表示信道矩阵中的第j行,所以,经过第k+1步选择后获得的系统容量为 (8) 根据矩阵乘法性质 (9) 代入式(8)得到 (10) 令 (11) (12) 从式(10)中可以看出,在第k+1步选择中,C(Hk+1)最大化等效于在待选集合中选择使μk,j最小的天线元素,即 (13) 利用矩阵求逆引理更新Dk+1得到 (14) (15) 采用如下递推公式,将每次计算变成实时更新 (16) 表2 双向搜索算法的具体步骤及相应的复杂度Tab.2 Bidirectional search algorithm and the corresponding complexity 为了分析双向搜索算法的性能,本文作者将双向搜索算法与若干典型的天线选择算法——最大范数算法(选取欧氏范数最大的前Lr行)、递增选择算法、递减选择算法、最优选择算法(穷举算法)及随机选择算法进行对比分析.仿真环境为瑞利平坦衰落信道,发射天线与接收天线完全不相关,信道矩阵各元素为独立同分布的循环复高斯随机变量.假设MIMO系统有4根发射天线,16根接收天线进行接收端天线选择. 3.1 容量与选择天线数的关系 图2给出了分别采用不同天线选择算法获得的容量与选择天线数的关系曲线(信噪比为20 dB).从图2中可以看到,系统容量随着选择天线数的增加也在不断上升.最优选择算法与随机选择算法获得的容量分别是容量曲线的上下边界,递减选择算法、双向搜索算法及递增选择算法的性能都比较接近最优算法,而最大范数算法与最优算法仍存在比较大的差距.通过局部放大图,可以更清晰的看出递增、递减选择算法及双向搜索算法之间的关系,递减选择算法曲线最接近最优选择,这是因为递减选择算法在进行每一次天线选择的时候,都考虑到了剩余天线的联合贡献,而由于递增选择算法在每次循环中只考虑增加天线的贡献,所以性能稍差.双向搜索算法的性能优于递增选择算法,略差于递减选择算法,这是因为双向搜索算法综合了递增与递减选择算法的特点,在保证性能同时没有增加计算复杂度. 3.2 容量与信噪比的关系 图3显示了在选择天线数固定(Lr=4)的前提下,分别采用不同天线选择算法获得的容量与信噪比的关系曲线.由图3可知,信道容量伴随着信噪比上升也在不断上升,最优选择算法与随机选择算法依旧是容量曲线的上下边界,最大范数算法与最优选择算法的差距在信噪比较低时并不明显,当信噪比逐渐增大时,两者之间的差距越来越大.从局部放大图可以清晰的看到与图2相同的位置关系,双向搜索算法的结果位于递减选择算法与递增选择算法之间.以上说明双向搜索算法对于不同的信噪比都有较强的适应能力. 3.3 算法运行时间与选择天线数的关系 图4给出了不同算法的运行时间随着选择天线数变化的关系曲线.为了便于观察,在仿真中将每个算法在给定选择天线数的条件下执行10 000次,分别记录算法总的运行时间.由图4可知,随着选择的天线数增加,递增选择算法的运行时间也随之增加,递减选择算法的运行时间则随着选择天线数的减少呈上升趋势,而双向搜索算法的运行时间随着选择天线数的增加先增大后减小,在Lr=Nr/2处取得最大值,双向搜索算法的运行时间的波动范围明显小于前两者,其主要原因是前两种算法的迭代次数与选择天线数基本呈线性关系,最大迭代次数为Nr.递增选择算法从空集开始选择,适用于选择天线数较少(Lr≤Nr/2)的情况,递减选择算法从全集开始选择,更适合选择天线数较多(Lr≥Nr/2)的情况,如果将前两种算法用于相反的情况,则迭代次数将不可避免的增加.双向搜索算法在每次循环中同时处理两根天线,相当于减少了一半的迭代次数,将最大迭代次数从Nr降低到Nr/2;同时采用了从两侧逼近的方式,在算法中保存两个天线子集变量,任意一个达到指定的天线数即完成选择,这一策略保证了双向搜索算法在不同的选择天线数条件下都能快速得出结果,能够灵活应对不同的选择天线数需求. 1)本文作者针对大规模MIMO系统中多变的信道环境,基于递增与递减天线选择算法,提出了双向搜索天线选择算法,双向搜索选择算法分别利用递增与递减选择算法,从空集与全集开始搜索,向指定天线子集逼近,在每次循环中,根据递增选择算法选出容量增益最大的一根天线,同时利用递减算法去掉容量损失最小的一根天线,每个循环会选择出一大一小两个天线子集,任意一个达到指定的天线数即完成选择.与每次只处理一根天线相比,能够更快获得所需的天线子集. 2)双向搜索算法综合了递增与递减选择算法的优点,在不增加计算复杂度的前提下,达到略优于递增选择算法的性能.与单一的递增或者递减选择算法相比,在面对多变的信道状态时,双向搜索算法更有优势.双向搜索算法的缺点是程序运行过程中需要更多的存储空间以保存迭代数据,而现在存储介质的价格越来越便宜,这一缺点也比较容易克服. [1] MARZETTA T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE Transactions on Wireless Communications, 2010, 9(11):3590-3600. [2] RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO: opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2012, 30(1):40-60. [3] BOCCARDI F, HEATH R W, LOZANO A, et al. Five disruptive technology directions for 5G[J]. Communications Magazine IEEE, 2013, 52(2):74-80. [4] LARSSON E, EDFORS O, TUFVESSON F, et al. Massive MIMO for next generation wireless systems[J]. IEEE Communications Magazine, 2013, 52(2):186 - 195. [5] AI B, GUAN K, RUPP M, et al. Future railway services-oriented mobile communications network[J]. IEEE Communications Magazine, 2015, 53(10):78-85. [6] AI B, CHENG X, KURNER T, et al. Challenges toward wireless communications for high-speed railway[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5):2143-2158. [7] SANAYEI S, NOSRATINIA A. Antenna selection in MIMO systems[J]. IEEE Communications Magazine, 2004, 42(10):68-73. [8] CHEN Z, VUCETIC B, YUAN J, et al. Analysis of transmit antenna selection/maximal-ratio combining in Rayleigh fading channels[J]. IEEE Transactions on Vehicular Technology, 2005, 54(4):1312-1321. [9] GOROKHOV A. Antenna selection algorithms for MEA transmission systems[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing , 2002: 2857 - 2860. [10] GHARAVI-ALKHANSARI M, GERSHMAN A B. Fast antenna subset selection in MIMO systems[J]. IEEE Transactions on Signal Processing, 2004, 52(2):339-347. [11] DONG K, PRASAD N, WANG X, et al. Adaptive antenna selection and Tx/Rx beamforming for large-scale MIMO systems in 60 GHz channels[J]. Eurasip Journal on Wireless Communications & Networking, 2011,59(4):1451-1459. [12] FANG B, QIAN Z, SHAO W, et al. RAISE: A new fast transmit antenna selection algorithm for massive MIMO Systems[J]. Wireless Personal Communications, 2015, 80(3):1147-1157. [13] GKIZELI M, KARYSTINOS G N. Maximum-SNR antenna selection among a large number of transmit antennas[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5):891-901. [14] GAO X, EDFORS O, TUFVESSON F, et al. Massive MIMO in real propagation environments: Do all antennas contribute equally[J]. IEEE Transactions on Communications, 2015, 63(11):3917-3928. [15] KAILATH T. Linear systems[M]. Englewood Cliffs, NJ: Prentice-Hall, 1980. [16] LU J, ZHANG L, CHEN C. Improved incremental and decremental antenna selection algorithms for MIMO systems[C]. 8th International Conference on Signal Processing, 2006. [17] 盛延敏, 奚宏生, 王子磊,等. 一种用于MIMO系统的快速天线选择算法[J]. 电子与信息学报, 2006, 28(9):1703-1705. SHENG Yanmin, XI Hongsheng, WANG Zilei, et al. A fast antenna selection algorithm in MIMO system[J]. Journal of Electronics & Information Technology, 2006, 28(9):1703-1705. (in Chinese) Bidirectional search antenna selection algorithm in Massive MIMO system LIULiu,CHISheng,LIUKai,TAOCheng (School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044,China) Massive multiple-input multiple-output (Massive MIMO) has a large number of antennas, so the hardware cost and system complexity will increase significantly if equal RF chains are installed in the conventional way.Antenna selection technology can effectively reduce the cost of RF chains without impairing the advantages of multi-antenna systems which is to choose partial antennas to transmit or receive data from all the antennas, so the MIMO communication system is no longer completely limited by RF cost. For a practical wireless channel, channel states are variable. In order to achieve the required performance, communication systems need to select a different number of antennas for data transmission, however, the present antenna selection algorithms are typically suitable for a fixed number of antennas.In this paper, we propose a bidirectional search antenna selection algorithm based on incremental and decremental antenna selection algorithms for variable channel states, which can flexibly meet the demand for the different number of antennas and maintain a lower computational complexity. Massive MIMO system;antenna selection;bidirectional search; incremental selection;decremental selection 2016-06-15 北京市科技新星计划项目资助(xx2016023);中央高校基本科研业务费专项资金资助(2015JBM011);国家自然科学基金面上 项目资助(61471027);东南大学移动通信国家重点实验室开放研究基金资助项目(2014D05);北京市自然科学基金资助项目(4152043) 刘留(1981—),男,云南昆明人,副教授,博士.研究方向为无线信道测量与建模和宽带无线接入物理层信号处理关键技术.email:liuliu@bjtu.edu.cn. TN929.5 A 1673-0291(2016)05-0056-07 10.11860/j.issn.1673-0291.2016.05.0102 双向搜索天线选择算法


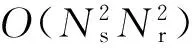

3 仿真结果与分析
4 结论

