直线感应电机的次级阻抗角计算及对涡流损耗的影响

吕 刚，刘素阔，周 桐

(北京交通大学 电气工程学院，北京 100044)



直线感应电机的次级阻抗角计算及对涡流损耗的影响

吕 刚，刘素阔，周 桐

(北京交通大学 电气工程学院，北京 100044)

为了解决电机涡流损耗过大对电机性能的影响，通过分析直线电机次级阻抗角，对电机涡流损耗进行研究.考虑了横向边缘效应，得到直线电机初级和次级耦合区气隙磁感应强度的解析表达式；建立电机的等效电路及次级涡流损耗分析模型，得到了次级阻抗角及涡流损耗的解析表达式.定量分析了次级阻抗角与次级涡流损耗的关系，定性分析了次级阻抗角对推力和侧向力的影响.以一台直线感应牵引电机为例，分别使用解析法和有限元方法对次级板的涡流损耗进行了计算，得到涡流损耗随频率变化的特性曲线.对比了两种方法的结果基本拟合，验证了本文解析表达式的正确性和易用性.

直线感应电机；涡流损耗；次级阻抗角；等效电路

地铁车辆采用直线感应电机技术具有很大的优势,不仅转弯半径小、牵引性能好和爬坡能力强,而且具有工程造价低、振动小和噪音低等特点.与其传统轮轨系统相比,直线电机技术的牵引系统在各方面都有着突出的优势[1].次级阻抗角的解析计算在旋转电机中比较常见，而在直线电机中比较少见，但是该角对直线电机的涡流损耗，三维力都很重要，因此本文对次级阻抗角进行分析计算.

次级涡流损耗问题是衡量直线感应牵引电机优劣的重要指标.文献[2]撰写了有关涡流分析的专著.文献[3]中采用有限元法对高速旋转电机的涡流损耗进行了分析.文献[4-5]对旋转电机的涡流损耗进行了分析.但是直线电机由于具有边缘效应，并不能直接把旋转电机的理论分析应用到直线电机中.

对于直线电机涡流损耗的研究大部分采用数值方法(如有限元法)，虽然数值方法能在考虑横向、纵向的情况下较准确地计算出直线电机次级板的涡流损耗[6-9]，但是所需时间较长，并且不能准确预测涡流损耗随各参数变化的趋势，不具一般性.还有一部分对直线电机次级板的涡流损耗采用解析法进行计算.

本文作者深入分析次级直线电机特性，通过修正系数，考虑横向边缘效应，给出直线感应电机等效电路和次级板涡流损耗分析模型.着重研究次级阻抗角，并分析该角对次级板涡流损耗的影响.

1 次级阻抗角的解析计算

直线电机等效电路如图1所示，次级阻抗角ψ2是次级板电流落后电动势的角度为

ψ2=arctan(xe)/re

(1)

(2)

即气隙磁场向前推进ψ2后次级板电流达到最大值.为求得次级阻抗角引入参数Da、Dj，所以ψ2为

(3)

式中:s是转差率 ；G是品质因数；Kp是有功功率因数；KQ是无功功率因数;re0和xe0是不考虑纵、横边缘效应时的电阻和电抗;re1和xe1是考虑横向边缘效应引入的电抗;re2和xe2是考虑纵向边缘效应引入的电抗;xm是激磁电抗.通过式(1～3)可得

(4)

为使式子简化,引入D1、D2、η2、λ2，所以Da和Dj可由以下式子得出[10]：

(5)

式中：f是频率；p是级对数；τ是极距；μ0是真空磁导率；折算后次级电导率γ′可由下式得出[10]：

(6)

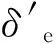
(7)

式中：t1是初级齿距；b0是初级槽口宽 ；lδ是初级宽度.

为确定系数Kp和KQ引入参数M、N，所以[10]：

(8)

M、N可由下式得出[10]：

(9)

其中：

(10)

式中,β是波数.由上述各式可得出次级阻抗角.

2 次级涡流损耗的分析模型

1)磁场与涡流如图2所示，在涡流中心位置建立坐标轴，得到行波磁场横向磁通密度平均值沿纵向的分布为

(11)

式中,横向磁通密度峰值的平均值为

(12)

分析有如下假设：1)无纵向端部效应;2)耦合区只有纵向电流dI(见图3);3)下层磁性次级无涡流损耗.

如图3所示，次极板涡流可以分为：横向电流和纵向电流，图3中，lδ是初级宽度;b是次级宽度，所以对于次级建立图4所示的分析模型.

在图4中，耦合区次级板的涡流，可以看成有许多矩形条状电流dI组成，之后耦合区内的电流汇聚到端部从端部流过，经过端部电阻形成涡流.

由于次级上层铝板较薄，并且电机运行时频率较低，所以不考虑集肤效应.有如下公式：

(13)

式中：c是次级板伸出次级板的宽度；Rdb是次级端部电阻；dR是每个矩形条状的电阻；E(x)是矩形条状上的电动势.所以，可得

(14)

(15)

式中，I2是次级板纵向的电流.所以一个涡流产生的损耗为

(16)

根据有限元仿真结果可以知道，非耦合区，也会有纵向的电流，因此耦合区的宽度，需要修正为alδ.次级伸出初级的宽度c需要修正为(b-alδ)/2.其中，a是修正系数，在1～b/lδ之间.

2)解析法计算如图5所示，当转差率是0.2时的涡流损耗.随着频率的增大，涡流损耗逐渐增大，由于次级板产生涡流增大，对气隙磁场的削弱作用增强，使得涡流损耗的增加逐渐趋于平衡.另外，通过对比可以发现由于次级阻抗角的存在明显增加了次级板的涡流损耗.

3 次级阻抗角对电机性能的影响

1)对推力的影响如图2所示.可知处于负方向磁场下的涡流有ψ2宽度的次级板电流密度与该磁场下其他次级板上的电流密度相反，所以它产生了与推力相反的力，会引起总推力的减小.

2)对侧向力的影响，当初级与次级发生侧向偏移的时候才会产生侧向力.假设没有侧向力情况如图6所示.图6中N表示磁场垂直纸面向里，S表示磁场垂直于纸面向外.此时，侧向力两边相互抵消，故不会产生侧向力，或者说由于涡流和磁场的不对称而产生很小的侧向力.

3) 由图5可以发现，次级阻抗角使次级板上的涡流损耗增加.考虑次级阻抗角时，如图7所示.

此时，侧向力并不会完全抵消.因为次级阻抗角和两板相对偏移同时存在，使得两板之间有侧向力的产生.

4 有限元仿真

Ansoft仿真参数见表1. 为验证解析法的正确性，根据表1的电机参数，建立直线电机有限元模型，如图8所示.

4.1 磁感应强度

如图9所示，在耦合区内，频率越高，解析法与有限元法得到的结果越一致.并且涡流产生的磁场对初级产生的磁场的抵消作用越强.解析法的缺点，

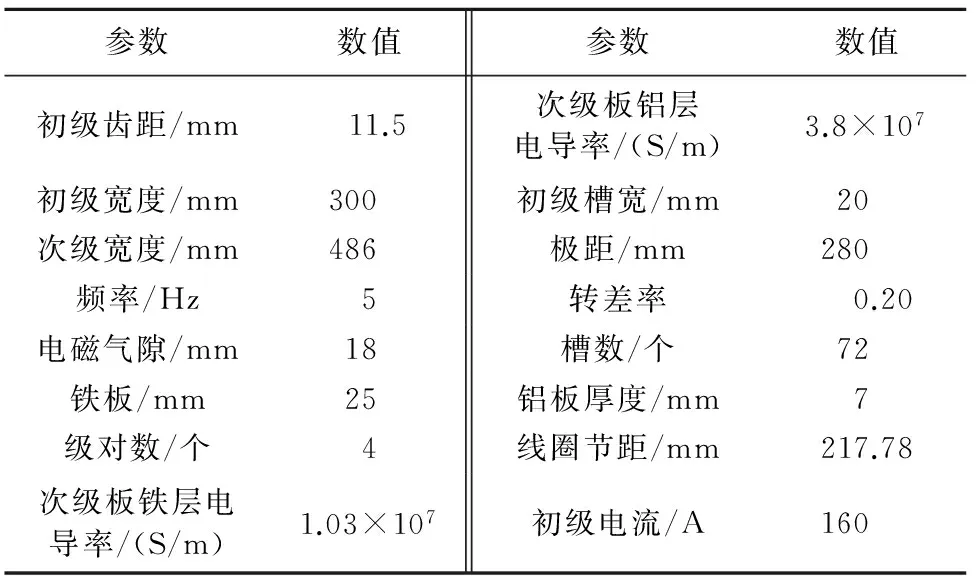
表1 电机参数Tab.1 Motor parameters

在于得不到非耦合区内的磁场分布.导致进行涡流损耗解析分析时，若不对耦合区的宽度进行修正，将会导致结果偏小.

4.2 次级阻抗角

次级阻抗角仿真结果的获得可通过有限元软件，记录磁场最小值xA与涡流中心点位置xB，用下式求得

(17)

图10为转差率是0.2时，有限元计算与涡流损耗计算所得次级阻抗角的比较.随着频率的增加，次级阻抗角逐渐减小，并且最后稳定在10°左右.说明随着频率的增大，次级阻抗角对涡流损耗的影响在减小，图10中，50 Hz以后两条曲线有靠近的趋势.

4.3 涡流损耗

图11为修正前、修正后有限元软件获得的涡流损耗与解析法获得的涡流损耗的比较，由于未考虑非耦合区的磁场，所以解析法所得的结果偏小.修正后，可以看出当频率较小时，解析法与有限元法较大误差；当频率较高时，误差较小.这与图10中的次级阻抗角有相同的变化规律，均是频率较高时解析法越准确.

5 结语

1)本文作者研究了直线电机的次级阻抗角，给出了次级阻抗角的解析表达式，用有限元软件验证了解析表达式的正确性.

2)定量研究了次级阻抗角与涡流损耗的关系，得出直线电机次级板涡流损耗随着次级阻抗角的增大而增大.

3)定性分析了次级阻抗角与推力和侧向力的关系,得出由于次级阻抗角的存在使直线电机的推力减小，使发生相对的偏移的初级和次级产生侧向力.

[1] 王燕芩.直线电机及其在城市轨道交通中的应用[J].中国西部科技, 2010, 9(29):1-2. WANG Yancen. Linear motor and its application in urban rail transit[J].Science and Technology of West China, 2010, 9(29):1-2. (in Chinese)

[2] STOLL R .The analysis of eddy currents[M]. Oxford: Oxford University Press, 1974.

[3] YAMAZAKI K, MIYAZAKI D, OHTO M, et al. Studies on electromagnetic field analysis of induction motors at high rotational speed[C]. The Papers of Meeting on Rotating Machinery,2007: 453-535.

[4] STOLL R L, HAMMOND P.Calculation of the magnetic field of rotating machines Part 4: Approximate determination of the field and the losses associated with eddy currents in conducting surfaces[J]. Proceedings of the Institution of Electrical Engineers, 1965, 112(11):2083-2094.

[5] YAMAZAKI K, TANIDA M, SATOMI H.Calculation of iron loss in rotating machines by direct consideration of eddy currents in electrical steel sheets[J].Electrical Engineering in Japan, 2011, 176(3):69-80.

[6] 吕刚, 范瑜, 马云双, 等. 直线感应电机推力和法向力的解析计算与分析[J]. 电机与控制学报, 2010, 14(3): 77-82. LYU Gang, FAN Yu, MA Yunshuang, et al. Characteristic analysis of linear induction traction motor for urban rail transit[J]. Electric Machines and Control, 2010, 14(3): 77-82. (in Chinese)

[7] KAIDO C, WAKISAKA T. Effect of material parameters on iron losses in non-oriented electrical steel sheets[J]. Transactions-Institute of Electrical Engineers of Japan A, 1997, 117(7): 685-690.

[8] PRESTON T W, REECE A B J.Transverse edge effects in linear induction motors[C].Proceedings of the Institution of Electrical Engineers, 1969, 116(6): 973-979.

[9] LU Q, LI Y, YE Y, et al.Investigation of forces in linear induction motor under different slip frequency for low-speed maglev application[J]. IEEE Transactions on Energy Conversion, 2013, 28(1):145-153.

[10] 上海工业大学,上海电机厂.直线异步电动机[M]. 北京：机械工业出版社,1979:65-140. Shanghai Industrial University, Shanghai Electric Machine Factory. Linear induction motor [M]. Beijing: Press of Mechanical Industry, 1979:65-140. (in Chinese)

Calculation of the secondary impedance angle of linear induction motor and its influence on eddy current losses

LYUGang，LIUSukuo，ZHOUTong

(School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044,China)

In order to solve the impact of the excessive eddy current loss on motor performance, this paper carries on studying motor eddy current loss by means of analyzing linear motor secondary impedance angle. Considering the transverse edge effects and the air-gap flux density in the coupled zone of the primary and secondary, the equivalent circuit of the single-sided linear induction motor (SLIM) and the analytical model of the eddy current loss in the secondary plate are presented for obtaining the analytical expression of the secondary impedance angle and the eddy current loss. This paper makes a quantitative analysis for the relationship between the secondary impedance angles and secondary eddy current losses, and a qualitative analysis of the effect of the secondary impedance angle on the thrust and lateral force. Taking a linear induction motor as an example, the eddy current loss of the secondary plate are calculated, and the eddy current loss with frequency characteristic curves are obtained by the analytical method and finite element method. By comparing the results of the two methods, the correctness and ease of the analytical expressions are verified.

linear induction motor; eddy current loss; secondary impedance angle; equivalent circuit

2016-05-11

国家自然科学基金资助项目(51377009)

吕刚(1976—)，男，河南焦作人，副教授.博士.研究方向为电力电子与电传动和电机与电器.email：ganglv@bjtu.edu.cn.

TM359.4

A

1673-0291(2016)05-0076-05

10.11860/j.issn.1673-0291.2016.05.013