提高初中数学课堂教学有效性的策略

詹凯

一、数学课堂教学低效的原因

初中数学课堂教学中经常出现这样的状况：教师为把更多的知识传授给学生，大多采用满堂灌的方法，题目逐道讲，内容逐点传授，知识逐步拓展延伸，生怕遗漏半点而使知识结构不完整，时时感到时间紧迫，而学生却听的索然无味、昏昏欲睡。“教师苦教、学生苦学”状况必然导致课堂教学低效甚至 无效。究其原因，主要有：

1.对教材理解的低效。没有充分领会教材编 写意图，生硬照搬教材内容。

2.对学生知识掌握程度理解的低效。忽视了学生的主体性和能动性。

3.课堂提问的低效。教学始于提问，而有的教 师在课堂中预设的问题是低效甚至无效的。

二、提高数学课堂教学有效性的策略

1.让学生思维“活”起来。函数贯穿于整个初中阶段，从七年级的变量初探到八年级一次函数、反比例函数再到九年级的二次函数，教材的设计由表及里、逐渐渗透，但对于学生来说，仍然是一个难点。

反比例函数部分综合性较强，需要学生有较好的数感和形感。华罗庚曾经说过，数缺形时少直观， 形缺数时难入微。而笔者所执教中学以农村学生为主，抽象思维能力相对较弱，必须使他们掌握数形结 合的思想方法，以不变应万变。

例1 已知反比例函数与一次函数的图象交于 A，B两点。

（1）求 A，B的坐标。

（2）x取何值时，一次函数的值大于反比例函数的值？

问题（1）相对简单，用方程组即可求得交点坐标。

对于问题（2），一些学生由2个函数值的不等关系想到不等式，问题由此而生：不等式如何解？不等式两边同时乘以x，得。新的问题又来了：x的取值直接影响不等号的方向，方向需要改变吗？学生在自我反问中发现了问题，但 、苦于探寻不出解决方案。此时，启发他们：如果把2个函数图象在同一直角坐标系中画出来会怎样？通过观察函数图象（见图1），学生豁然开朗，要使一次 函数的值大于反比例函数的值，只要对应的一次函 数图象位于反比例函数图象的上方即可。这时，自变量的取值范围如何确定呢？过A，B两点作x轴的垂线便知。看似单纯的代数问题，借助于几何图像有时更易解决。

2.让课堂教学“动”起来。与其他知识相比，函数知识枯燥、抽象，逻辑性强。在教学中，要重视学生的自主探究，做到师生互动、生生互动，激发学生思维的闪光点。

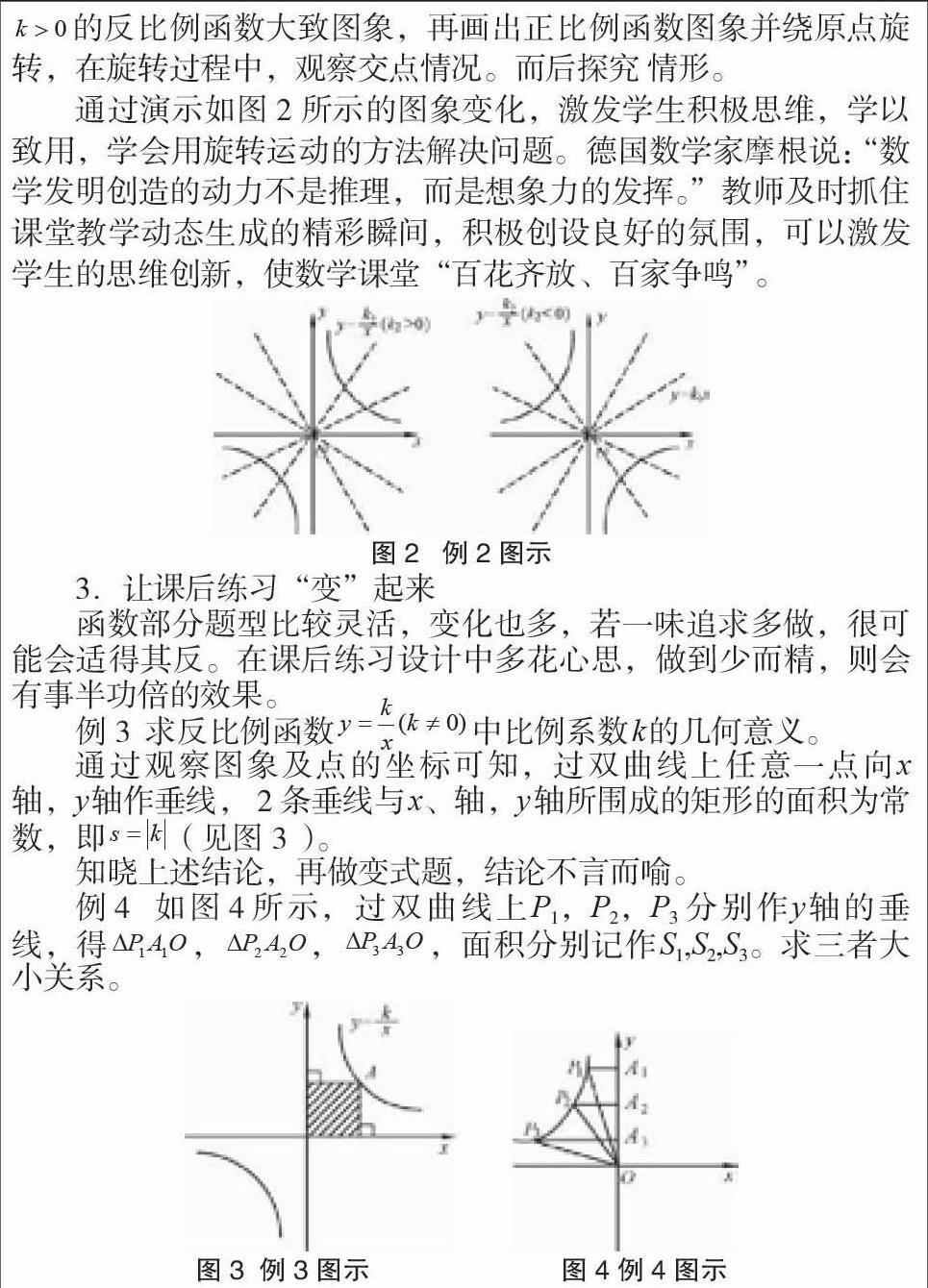
例2 若函数与的图象无交点，则k1，k2应满足什么条件？

学生首先想到方程组，得知k1，k2异号。

从方程的角度可以解决，能否用图象解决呢？k1，k2未知，如何画出准确的函数图象呢？学生通过讨论发现，反比例函数和正比例函数图象具有相同的象限特点，即过第一、第三象限或过第二、第四象 限，而且若一个经过第一、第三象限，而另一个经过 第二、第四象限，则必无交点。有的学生则更进一步，先画出的反比例函数大致图象，再画出正比例函数图象并绕原点旋转，在旋转过程中，观察交点情况。而后探究 情形。

通过演示如图2所示的图象变化，激发学生积极思维，学以致用，学会用旋转运动的方法解决问题。德国数学家摩根说：“数学发明创造的动力不是推理，而是想象力的发挥。”教师及时抓住课堂教学动态生成的精彩瞬间，积极创设良好的氛围，可以激发学生的思维创新，使数学课堂“百花齐放、百家争鸣”。

3.让课后练习“变”起来

函数部分题型比较灵活，变化也多，若一味追求多做，很可能会适得其反。在课后练习设计中多花心思，做到少而精，则会有事半功倍的效果。

例3 求反比例函数中比例系数k的几何意义。

通过观察图象及点的坐标可知，过双曲线上任意一点向x轴，y轴作垂线，2条垂线与x、轴，y轴所围成的矩形的面积为常数，即（见图3）。

知晓上述结论，再做变式题，结论不言而喻。

例4 如图4所示，过双曲线上P1，P2，P3分别作y轴的垂线，得，，，面积分别记作S1，S2，S3。求三者大小关系。

用典型练习引导学生掌握解决问题的方法，可以在潜移默化中让学生端正学习态度，养成良好的 解题习惯。所以，笔者在课后练习中给出以下2道思考题：

（1）在一次函数的图象上任取一点A，过A分别作 x轴，y轴的垂线，围成一个矩形，这个矩形的面积是定值吗？如果不是，你猜想这个矩形的哪一个量是定值？

（2）能否找到一个矩形，面积为4，而周长为12？面积为1，周长为3的矩形如何找？

学生明白反比例函数、一次函数图象的意义，并能从本质上区分2类函数变量之间的关系，结合方程知识和函数图像即可解决。

三、结语

数学学习是连续的，教师的作用不容忽视。教师要做到：课前精心选择示范例题，有备而来；课中悉心讲授内容，引导学生主动参与、自主发现；课后细心挑选练习内容，给予学生无限发展的空间。坚持师生之间的交流与沟通，让每一位学生都走上属于自己的成功之路。

参考文献：

[1]余文森.简论学生学习方式的转变[J].

[2]王新民.关于数学教学效率及其效率意识的分析[J].数学教育学报.

[3]中华人民共和国教育部.全日制义务教育数学课程标准 （修改稿）[M].北京：北京师范大学出版社.