带有交货期窗口和加工时间可控的排序问题

赵传立, 张 蕾

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)



带有交货期窗口和加工时间可控的排序问题

赵传立, 张 蕾

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

讨论了带有交货期窗口和加工时间可控的单机排序问题。工件的加工时间是关于分配资源量的凸函数模型。工件若在交货期窗口前完工,则产生提前费用;若在交货期窗口后完工,则产生延误费用。分别研究了多窗口问题和单窗口问题。目标是在关于提前、延误、交货期窗口开始时间、交货期窗口大小和最大完工时间的函数约束条件下,确定工件的最优加工顺序、最优加工时间、极小化资源费用函数。通过将2个问题分别转化为指派问题,证明了2个问题是多项式时间可解的,问题的计算复杂性是O(n3)。

排序; 单机; 交货期窗口; 加工时间可控; 多项式时间算法

0 引 言

在经典的排序模型中,每个工件有固定的加工时间,但在实际的生产过程中,工件的加工时间并不是不变的,可能会受到退化效应、学习效应、分配的资源量、工件的加工位置等因素的影响。近年来,关于加工时间可控的排序问题的研究越来越多。Liu等[1]研究了带有交货期窗口和加工时间是关于资源量的凸函数模型的单机排序问题,目标是在约束条件下极小化资源消耗费用之和,给出了多项式时间算法,计算复杂性为O(nlogn)。Yang等[2]讨论了带有多个交货期窗口和加工时间可控的排序问题,针对多个目标函数分别给出了多项式时间算法。Yang等[3]对带有维修活动和可控加工时间的平行机问题进行了研究,目标是极小化总完工时间,证明了该问题是多项式时间可解的。Rudek等[4]研究了带有资源的流水作业的排序问题,目标是极小化最大完工时间,给出了多项式时间算法。Shabtay等[5]对于加工时间可控的若干排序问题做出了详细综述。

在带有交货期窗口的排序问题中,提前、延误完工都会产生相应的惩罚。赵传立等[6]考虑了带有交货期窗口和维修活动的单机排序问题。工件的加工时间为所在位置的非减函数模型,通过将问题分别转换为指派问题,证明了该问题是多项式时间可解的。Mor等[7]提出了带有维修活动和多窗口的单机排序问题,通过对不同类型的维修活动进行分析,给出了计算复杂性O(n4)的多项式时间算法。Wang等[8]提出了具有学习效应、资源和交货期窗口的单机排序问题,并且证明了该问题是多项式时间可解的,给出了计算复杂性为O(n3)的多项式时间算法。Yin等[9]研究了每个工件都有自己的交货期窗口和加工时间可控的单机排序问题,证明了该问题是多项式时间可解的。Wang等[10-11]讨论了同时带有学习效应、退化效应和交货期窗口的排序问题,分别给出了多项式时间算法。Zhao等[12]研究了所有工件有一个共同的交货期窗口,并且带有退化效应和维修活动的单机排序问题,目标是极小化提前、延误、交货期窗口开始时间、交货期窗口大小总费用函数,并且给出了多项式时间算法,证明了该问题是多项式时间可解的。

在文献[1]的基础上,对带有交货期窗口和加工时间是关于资源的凸函数模型的排序问题进行了研究,证明了该问题是多项式时间可解的。

1 问题描述

设有n个工件{J1,J2,…,Jn}在1台机器上加工,所有工件零时刻到达,机器在同一时间只可加工1个工件,加工过程不可中断。考虑的加工时间模型如下:

其中:wj≥0是工件Jj的基本加工时间;r是工件Jj在排序中所处的位置;aj≤0(aj≥0)是工件Jj的学习率(退化率);uj>0是分配给工件Jj的资源量;k是正参数。

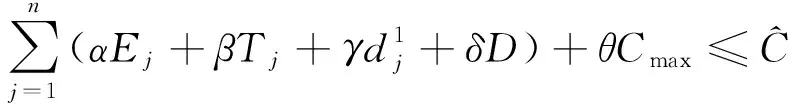
引用三参数表示法将本文所要研究的问题表示成

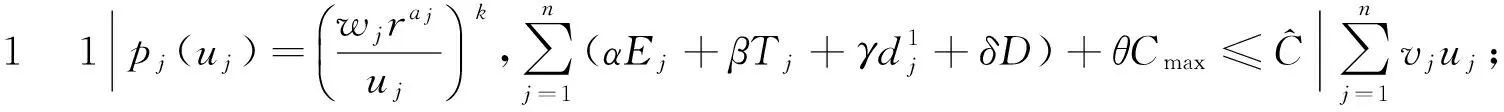
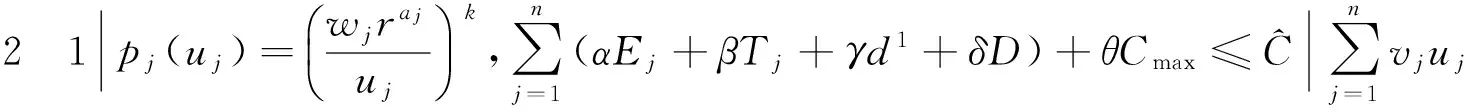
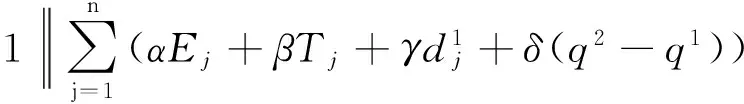
1) 每个工件的加工不可中断,机器无空闲状态,第1个工件在零时刻开始加工;

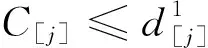
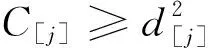
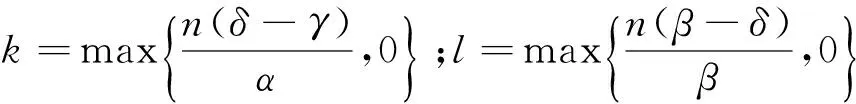
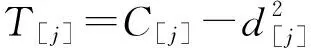
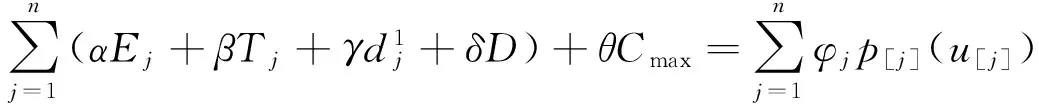
(1)

(2)

证明 给定的一个排序π=(J[1],J[2],…,J[n]),由拉格朗日乘子法,设

(3)

对于式子(3),分别对u[j],λ求偏导,可以得到

(4)

(5)

由式(4)得到

(6)

则

(7)

由式(5)和式(7)得到

(8)

则

(9)

将式(9)代入式(7),得到式(2)。

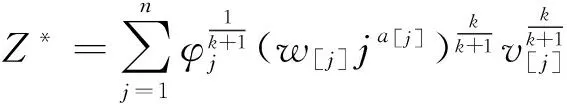
考虑到问题1是针对全部排序,求Z*的最小值可以通过指派问题进行求解,设

(10)

定义变量χij,如果工件i排在第j个位置上,则χij=1;否则,χij=0。

则问题1转化为下列指派问题

算法1

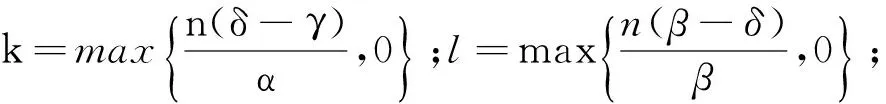
步骤2 通过式(10)计算τij,i=1,…,n,j=1,…,n;

步骤4 通过解决指派问题Z*,确定工件的最优排序,记最优排序为π*=(J[1],J[2],…,J[n]);

证明 算法1中,步骤4的计算复杂性为O(n3),步骤1、2、3均可以在线性时间内解决。因此,算法1整体的计算复杂性为O(n3)。

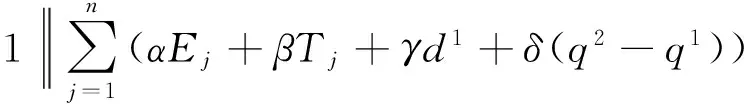
1) 每个工件的加工不可中断,机器无空闲状态,第1个工件在零时刻开始加工;

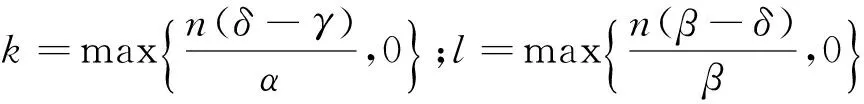
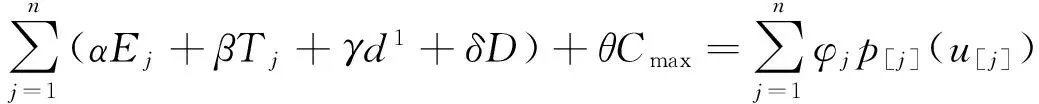
(11)

(12)

证明同上一问题。

φj可通过式(11)计算得到,

同理,Z*可以通过指派问题进行求解,设

(13)

定义变量χij,如果工件i排在第j个位置上,则χij=1;否则,χij=0。

则问题2转化为下列指派问题

算法2

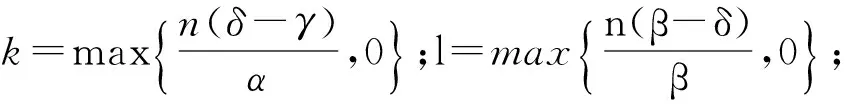
步骤2 通过式(13)计算τij,i=1,…,n,j=1,…,n;

步骤3 通过式(12)计算出最优资源分配量u*[j],j=1,…,n;

步骤4 通过解决指派问题Z*,确定工件的最优排序,记最优排序为π*=(J[1],J[2],…,J[n]);

证明 算法2中,步骤4的计算复杂性为O(n3),步骤1、2、3均可以在线性时间内解决。因此,算法2整体的计算复杂性为O(n3)。

4 结 论

讨论了带有交货期窗口和加工时间可控的单机排序问题。工件的加工时间受工件的基本加工时间、工件的加工位置、学习率(退化率)、分配的资源量影响。在关于提前、延误、窗口开始时间、窗口大小、最大完工时间的总费用函数的约束条件下,极小化资源费用函数。通过对多窗口和单窗口问题的分别讨论,将问题转换成了相应的指派问题,构造了多项式时间算法,证明了所研究的问题是多项式时间可解的。进一步的研究可以考虑其他单机或平行机问题。

[1]LIU Lu,WANG Jianjun, WANG Xiaoyuan. Single machine due-window assignment scheduling with resource-dependent processing times to minimize total resource consumption cost[J]. Int J Prod Res, 2016,54(4):1186-1195.

[2]YANG D L, LAI C J, YANG S J. Scheduling problems with multiple due windows assignment and controllable processing times on a single machine[J]. Int J Prod Econ, 2014,150:96-103.

[3]YANG D L, CHENG T C E, YANG S J. Parallel-machine scheduling with controllable processing times and rate-modifying activities to minimize total cost involving total completion time and job compressions[J]. Int J Prod Res, 2014,52(4):1133-1141.

[4]RUDEK A, RUDEK R. On flowshop scheduling problems with the aging effect and resource allocation[J].Int J Adv Manuf Technol, 2012,62(1):135-145.

[5]SHABTAY D, STEINER G.A survey of scheduling with controllable processing times[J]. Disc Appl Math, 2007,155(13):1643-1666.

[6]LI Weixuan, ZHAO Chuanli.Single machine due window assignment and scheduling with an optional maintenance activity[J]. Adv Mater Res, 2014,1006/1007:437-440.

[7]MOR B, MOSHEIOV G. Scheduling a deteriorating maintenance activity and due-window assignment[J]. Comput Oper Res, 2015,57:33-40.

[8]WANG Jibo, WANG Mingzheng. Single-machine due-window assignment and scheduling with learning effect and resource-dependent processing times[J]. Asia Pac J Oper Res, 2014,31(5):1450036.

[9]YIN Y Q, CHENG T C E, WU C C, et al. Single-machine due window assignment and scheduling with a common flow allowance and controllable job processing time[J]. J Oper Res Soc, 2014,65(1):1-13.

[10]WANG Jibo, WANG Cheng. Single-machine due-window assignment problem with learning effect and deteriorating jobs[J]. Appl Math Model, 2011,35(8):4017-4022.

[11]WANG Jibo, LIU Lu, WANG Cheng. Singlemachine SLK/DIF duewindowassignment problem with learning effect and deteriorating jobs[J]. Appl Math Model, 2013,37:8394-8400.

[12]ZHAO Chuanli, TANG Hengyong. A note to due-window assignment and single machine scheduling with deteriorating jobs and a rate-modifying activity[J]. Comput Oper Res, 2012,39(6):1300-1303.

[13]MOSHEIOV G,ORON D. Job-dependent due-window assignment based on a common flow allowance[J]. Found Comput Dec Sci, 2010,35(3):185-195.

[14]WU Yubin, WAN Long, WANG Xiaoyuan. Study on due-window assignment scheduling based on common flow allowance[J]. Int J Prod Econ, 2015,165:155-157.

[15]LIMAN S D, PANWALKAR S S, THONGMEE S. Common due window size and location determination in a single machine scheduling problem[J]. J Oper Res Soc, 1998,49(9):1007-1010.

Single machine due-window assignment and scheduling with controllable processing times

ZHAOChuanli,ZHANGLei

(College of Mathematics and Systems Science,Shenyang Normal University, Shenyang 110034, China)

In this paper, we consider a kind of single-machine scheduling problem with due-window assignment and scheduling with controllable job processing times. The processing time of each job is the convex resource function. If the job is completed outside the due-window, it would be penalized according to its earliness or tardiness value. We consider two models. In the first model, each job has its own due-window.In the second model, all the jobs have the common due-window. The objective is to determine the optimal sequence, the optimal processing times and to minimize the total resource consumption cost under the constraint that the scheduling cost is related to earliness, tardiness, the starting time of due-window, the size of due-window and the makespan. By converting the two scheduling problems into assignment problems, we prove that the scheduling problems can both be solved in polynomial time and the complexities of the two problems are bothO(n3).

scheduling; single machine; controllable processing time; polynomial time

2016-07-08。

辽宁省教育厅科学研究一般项目(L2014433)。

赵传立(1958-),男,黑龙江泰来人,沈阳师范大学教授,博士。

1673-5862(2016)04-0402-07

运筹学与控制论

O223

A

10.3969/ j.issn.1673-5862.2016.04.005