污染负荷优化分配的非线性规划模型

林高松(深圳市环境科学研究院 广东 深圳 518001)

黄晓英(深圳市汉宇环境科技有限公司 广东 深圳 518001)

污染负荷优化分配的非线性规划模型

林高松(深圳市环境科学研究院 广东 深圳 518001)

黄晓英(深圳市汉宇环境科技有限公司 广东 深圳 518001)

基于线性规划的污染负荷优化分配结果通常存在“极端化”现象，分配方案的合理性、可行性和公平性均受到影响。针对该问题，提出了一种污染负荷优化分配的非线性规模模型，以最小化污染物削减率方差为目标，允许决策者根据偏好调整最低允许负荷量，并采用遗传算法求解模型。研究结果表明，非线性规划模型能够较好地解决线性规划存在的“极端化”现象，计算结果在公平合理性方面获得较大改进，并且具有较大的弹性，有利于提供更科学、合理的污染负荷分配方案。

污染负荷分配；优化；非线性规划

环境容量是环境科学的基本理论问题之一。污染负荷分配方法是求解环境容量的关键技术。为充分利用水体的自净能力，通常在满足环境目标的前提下，根据优化原则确定各排污口允许负荷量，使总负荷量最大或总削减量最小，以实现经济效益与环境效益的最佳结合。污染负荷优化分配方法包括模型试算法和系统最优化法。模型试算法简单实用，但计算效率低，适用范围十分有限。大多数情况下，系统优化是最有效的分配手段。

污染负荷的系统优化主要通过数学规划模型实现，即从系统观点出发，根据污染源的空间格局和排放强度以及污染治理的技术经济水平，求出最优的污染负荷分配方案。线性规划是最早并且发展最完善的数学规划方法，20世纪60年代国外已有学者将其应用于河流水质管理，也是目前在国内外污染负荷优化分配领域中应用最广的方法。但是，线性规划的计算结果往往有缺陷。其一是最优解存在“极端化”现象，即计算值要么是约束条件的下限，要么是上限，使得污染负荷过多地集中在少数排污口，而部分排污口的允许负荷量为0，尽管数学上达到最优解，但实际应用时不一定符合要求；其二是优化结果完全忽略公平问题，实际可行性受到较大影响；其三是缺乏弹性和可比性，例如次优解的总负荷量比最优解略小，但污染负荷在各排污口中的分布更为合理，而计算结果只提供最优解，不利于决策者通过比较选择更理想的方案。

针对上述问题，本文在现有的线性规划模型的基础上，提出一个污染负荷优化分配的非线性规划模型，以获得更合理和更有弹性的方案，为总量控制提供决策支持。

1 线性规划模型

1.1 总允许负荷量最大化的线性规划模型

为了充分利用河流的纳污能力，可采用总允许负荷量最大化为目标建立污染负荷优化分配模型，即在选定的一组水质控制点的污染物浓度不超过其各自对应的环境标准的前提下，各排污口的允许负荷量之和最大。其数学表述如下：

式中，TL为总允许负荷量；x为排污口的允许负荷量，i为排污口编号，m为排污口个数；aij为排污口i对水质控制点j的污染贡献率，j为水质控制点编号，L为水质控制点个数；cb为水质控制点的背景浓度值，cs为水质控制点的环境标准值。

式(1)为模型的目标函数，使总允许负荷量最大化；式(2)为总负荷量的定义；式(3)为水质达标约束条件，即要求分配结果不得使水质控制点的浓度超标；式(4)非负约束条件，排污口的允许负荷量是非负数。

式(1)～(4)是基于总允许负荷量最大化的线性规划模型，其特点是完全根据水体自净能力分配各污染源的允许负荷量，优化结果反映了水域的最大纳污能力。如果污染源对环境影响较小，获得的负荷量必定较多，反之则少，从而使水域所能容纳的总污染负荷量最大，充分地利用环境容量资源。这对区域发展规划布局具有重要指导意义。

1.2 总削减量最小化的线性规划模型

一般情况下，区域的社会经济已发展到一定程度，已形成某种排污格局，而上述模型对现状排污量没有加以考虑，最优解可能与现实脱节。譬如，在水质超标的河流中，某些排污口获得的允许负荷量大于其现状排放量，实际上占用了其它排污口的环境容量资源，其它排污口被迫作出更多的削减，反而导致总削减量和削减费用增加。因此，如果从总削减量最小化角度考虑，需要增加排污口负荷量的上限约束条件：

式中，ximax为排污口i的最大允许负荷量，一般可取现状排污量。

式(1)～(5)是基于总削减量最小化的线性规划模型。由于增加了式(5)，允许负荷量不会过多地分配到不需要继续削减排放量的排污口，而是转移到其他削减率较高的排污口，从而使总削减量最小化。

2 非线性规模模型

如前所述，线性规划模型可能存在弊端，包括计算结果“极端化”问题、完全忽略公平合理性、分配方案单一和缺乏弹性等。因此，本文设计一种污染负荷分配的非线性规划模型，其数学表述如下：

式中，ηi为排污口i的削减率，η为平均削减率，f是削减率的方差。wi为排污口i的现状排放量，TL*为设定的最低允许负荷量，其余变量含义同上。

式(6)为目标函数，目的是使各排污口的削减率尽可能平均，一方面对排污者较为公平，另一方面允许负荷量分布也较为合理。式(7)～(8)为削减率和平均削减率的定义；式(11)为最低允许负荷量约束条件，即分配方案的总负荷量不得低于某设定值TL*，以保持一定的优化布局特征。一般而言，可以事先采用式(1)～(5)求出最大负荷量TL，决策者以此为参照给出TL*(TL*≤TL)。

式(6)-(11)是允许负荷优化分配的非线性规划模型。模型目标函数是最小化削减率的方差，可避免部分排污口削减率过高或过低的问题；同时，决策者可通过调整TL*获得不同的分配方案，并选择最满意的分配结果，决策过程更具弹性。

3 模型的求解方法

线性规划模型可采用较为成熟的单纯形法求解。非线性规划模型则相对复杂，不能用单纯形法计算，本文采用遗传算法求解。

遗传算法(genetic algorithm，简称GA)是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。自从20世纪60年代Michigan大学的Holland教授首次提出GA的思想以来，经过众多学者的努力，已获得极大的发展和完善。目前，GA在各个领域的优化问题中均获得广泛应用。

GA借鉴了生物遗传学的观点，对当前种群施加选择、交叉、变异等操作，并实行“物竞天择，适者生存”的自然进化过程，通过不断进化而产生最优个体。计算过程包括生成初始种群、评价个体适应度、选择与交叉、选择与变异等运算，生成新一代种群。经过多次迭代进化，以最优个体作为问题的最优解。GA的流程如图1所示，算法步骤的具体内容可参考文献。GA的优化效果在文献中已进行了验证，在此不作赘述。其优点是对目标函数和约束条件没有特殊要求，适用性极强，可用于求解各类优化问题。

图1 遗传算法流程

4 研究案例

以佛山水道为例，比较不同规划模型计算结果的差异。佛山水道包括汾江和佛山涌，是广东省佛山市区的主要纳污水体，以COD为指标污染物，计算各排污口的允许负荷量。

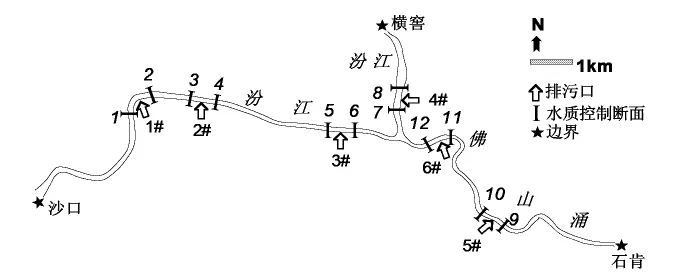
图2 佛山水道示意图

计算步骤如下：

(1)对研究河段进行概化处理。根据实际情况，将沿河的排污口概化成6个，每个排污口上下游200m各设立一个水质控制断面，共设立12个控制断面，如图2所示。

(2)利用水环境数学模型计算出各排污口对控制断面的污染贡献率以及控制断面的背景浓度值，即式(3)和式(9)中的变量aij和cbi。佛山水道为感潮河流中，需要采用一维潮汐河网动态水环境数学模型计算。由于aij和cbi是随时间变化中，因此取一个潮周期的平均值。水环境数学模型的验证以及aij和cbi的具体计算过程可参考文献。

(3)采用不同的分配模型求解各排污口的允许负荷量。方案Ⅰ和方案Ⅱ均为线性规划模型的计算结果，其中方案Ⅰ以总允许负荷量最大化为目标，即求解式(1)-(4)；方案Ⅱ为以总削减量最小化为目标，即求解式(1)-(5)，排污口的污染负荷上限ximax取现状排污量wi。方案Ⅲ为本文提出的非线性规划模型计算结果，即求解式(6)-(11)，由于TL*是由决策者指定的，现假设TL*=14t·d-1。计算结果如表1所示。

由计算结果可知，方案Ⅰ的总允许负荷量最大，达到16.63 t·d-1，但污染负荷仅分配至1#、4#、6#排污口，其余排污口的负荷量为0，“极端化”现象十分明显。同时，由于部分排污口未分配得允许负荷量，削减率为100％，导致总的削减量也最大，平均削减率到达87％，这与允许负荷分配过于集中有关。

表1 佛山水道的COD优化分配结果

方案Ⅱ的总削减量最小，平均削减率为73％。但“极端化”现象仍然较为明显，其中2#排污口的削减率达到100％。

方案Ⅲ为本文提出的非线性规划模型计算结果，虽然总允许负荷量比前两种方案小，但各排污口的削减率相对平衡，削减率在21％～90％之间，而且平均削减率均低于方案Ⅰ，与方案Ⅱ接近。

需要指出，在求取方案Ⅲ的过程中，TL*是由决策者指定的。一般而言，可先求取方案Ⅱ的最优解，TL*取值范围在0和方案Ⅱ的最优解之间。显然，TL*取值越大，优化特征越明显，但削减率的不均衡性(即“极端性”)也越大；当TL*取值越小，则污染物削减率越平均，分配方案的优化特性越低。决策者可以调整TL*，根据不同TL*可求出不同的优化结果，在均衡性与优化之间取得平衡，并选择最满意的方案。因此，非线性规划模型可根据决策者的偏好调整方案，具有较大的弹性。

5 结论

本研究在传统线性规划模型的基础上，设计了一种污染负荷优化分配的非线性规划模型，并且与总负荷量最大化和总削减量最小化的线性规划模型进行比较。研究结果表明：

(1)总负荷量最大化与总削减量最小化的线性规划模型可获得数值上最优解，但分配结果存在“极端化”现象，即污染负荷集中到少数排污口，而其他排污口的允许负荷量过低，影响了分配结果的合理性和公平性。

(2)非线性规划模型则可避免“极端化”现象，削减率相对平均，污染负荷不会过分集中。计算结果在公平合理方面获得较大改进，同时仍然保持一定的优化特征。

(3)线性规划模型的最优解是唯一的；本文提出的非线性规划可通过调整最低允许负荷量TL*求取不同的次优解，进而选择最合适的分配方案，具有较大弹性，便于决策者综合考虑效益与公平合理性进行决策。

〔1〕张永良.水环境容量基本概念的发展〔J〕.环境科学研究，1992，5(3)：59-61.

〔2〕董飞，刘晓波，彭文启等.地表水水环境容量计算方法回顾与展望〔J〕.水科学进展，2014，25(3)：451-463.

〔3〕徐祖信，卢士强.潮汐河网水环境容量的计算分析〔J〕.上海环境科学，2003，22(4)：254-257.

〔4〕裴相斌.基于GIS的海湾陆源污染排海总量控制的空间优化分配方法研究--以大连湾为例〔J〕.环境科学学报，2000，20(3)：294-298.

〔5〕金海生，郑英铭.潮汐河流一维动态COD水环境容量计算模型〔J〕.水利学报，1992(9)：15-22.

〔6〕李适宇，李耀初，陈炳禄等.分区达标控制法求解海域环境容量〔J〕.环境科学，1999，(4)：96-99.

〔7〕王经盛，陶涛.水环境容量计算在污水系统规划中的应用〔J〕.中国给水排水，2012，28(3)：82-85.

〔8〕田旭东，姜斌彤，俞洁等.生态环境功能区规划中水环境容量分配方法探讨〔J〕.环境污染与防治，2009，31(1)：83-89.

〔9〕荀方飞，葛亚军，马靖一.线性规划法在水环境容量计算中的应用〔J〕.水资源与水工程学报，2009，20(5)：180-182.

〔10〕王勤耕，李宗恺.城市大气污染源排污负荷优化分配模型〔J〕.环境科学学报，1996，16(4)：444-449.

〔11〕周明，孙树栋.遗传算法原理及应用〔M〕.北京：国防工业出版社，1999.

〔12〕刘宝碇，赵瑞清，王纲.不确定规划及应用〔M〕.北京：清华大学出版社，2003.

〔13〕中山大学环境科学研究所.广州、佛山跨市水污染综合整治方案〔R〕.广州，2002.

Non-linear Programming Model for Optimal Waste Load Allocation

LinGaosong(ShenZhen Academy of Environmental Science ShenZhen GuangDong 518001)

The linear programming model for waste load allocation usually results in extreme values，which leads to an optimal but infeasible allocation scheme.Therefore，a non-linear programming model for waste load allocation is proposed in this paper，whose goal is to minimize the variance of pollution reduction，and decision-maker is allowed to change the minimal permitted waste load.The genetic algorithm is used to establish the non-linear programming model.Study results show that the non-linear programming model can resolve the problem of extreme output created by linear programming model，and the calculation results obtain great improvement in fairness and reasonableness.Non-linear program model can provide more flexible and more scientific scheme for waste load allocation than that of traditional linear program model.

Waste load allocation Optimization Non-linear programming

X821

A

1674-263X(2016)04-0034-04

2016-12-26

林高松(1979-)，男，博士，高级工程师，从事环境科研工作。