基于Kriging模型及NSGA-Ⅱ算法的前围声学包优化

吴 宪， 王 成， 邵建旺， 邓国明

(同济大学 汽车学院，上海 201804)



基于Kriging模型及NSGA-Ⅱ算法的前围声学包优化

吴 宪， 王 成， 邵建旺， 邓国明

(同济大学 汽车学院，上海 201804)

利用统计能量分析方法，首先建立了计算汽车前围板传递损失的统计能量分析模型，采用最优拉丁超立方方法生成了36个声学包方案的试验点，其中以覆盖率、堵件厚度、PU泡沫厚度及EVA面密度为设计变量和以前围子系统隔声量和声学包重量为优化目标，并计算了不同声学包方案下前围子系统的传递损失。然后依此建立Kriging近似模型并验证模型的可信度，采用NSGA-Ⅱ算法进行以声学包隔声量及重量为目标的多目标优化，获得了Pareto最优解集。赋予声学包隔声性能及总重量一样的权重，得到了覆盖率、堵件厚度、PU泡沫厚度及EVA面密度的最优值，并任取三组试验点计算其传递损失和整车中的基于能量的隔声量和驾驶员头部的声压级，从而验证该结果的正确性。结果表明，该最优值能够使得声学包在隔声性能与重量之间取得最佳平衡。

声学包优化；最优拉丁超立方；Kriging模型；NSGA-Ⅱ算法

声学包是在从整车噪声源(动力总成、空气噪声、传动系、进排气、轮胎噪声等)到轿车车内传播路径中合理使用的手段，有效阻隔噪声在传播过程中传递的一种实用方法[1]。在整车的NVH开发进程中，声学包的设计和确定是其中一个关键步骤，它设计的好与坏直接影响着车内噪声水平。声学包通常指汽车NVH有关的各类吸音隔音部件的总和，如前围隔音隔热垫、顶棚、地毯等。它主要由无纺布、泡沫、毛毡等多孔、大阻尼材料组成，通过材料纤维之间的相互摩擦消耗中高频噪声能量，达到吸声隔声目的[2]。传统的声学包优化设计主要包括声学材料的替换，结构的优化或者是通过正交实验来确定最佳的泡沫厚度与EVA面密度组合等方法。这些方法一般很难得到声学包装材料参数的最优值，而文中采用的Kriging近似模型可以得到输入与输出之间的连续响应，通过非支配排序遗传算法(NSGA-Ⅱ)从而可以获得声学包装材料的全局最优值，避免了采用正交试验获得的局部最优，对声学包装材料的优化具有重要的意义。因此本文利用统计能量方法(SEA)建立某汽车前围子系统SEA模型，分析不同声学包方案下的传递损失，然后建立以板件声学包覆盖率、过孔堵件厚度、声学包装材料厚度及面密度四个重要影响因素为自变量，以隔声量和声学包重量为因变量的近似模型，并对该多目标优化问题进行求解，意在获得声学包装材料的最优参数。

1 前围SEA模型建立

本文选择某汽车前围的声学包作为研究对象，以该前围板有限元模型为基础，在VA One中根据子系统划分原则，建立21个平板子系统，其中包括7个孔板件，如图1所示，各个板件子系统如表1所示。同时验证每个子系统频带内的模态数均大于3，满足统计能量分析的要求。根据实际情况，定义前围板为1.2 mm的钢板，导水槽为1 mm的钢板。然后在前围板两侧生成声腔子系统，分别定义为声源腔和接受腔，两个声腔通过车身板件的面连接进行能量的传递，并在声源腔施加1 Pa的声压约束载荷。同时对生成的声腔进行检查和修改，以免出现能量泄漏。最终得到如图2所示的前围子系统SEA模型。

图1 前围板统计能量分析模型Fig.1 Statistical energy analysis (SEA) model of dash panel表1 前围各个板件子系统Tab.1 Different panel subsystems of dash

编号名称面积/mm2编号名称面积/mm21板5316012孔225902板14130013孔43553孔1778014板785404板15630015导水槽板655105板5228016导水槽板575806孔437817导水槽板550307孔300918板904808孔296319导水槽板631009板9179020导水槽板5806010孔145721导水槽板5472011板85000

1.声源腔；2.接收腔 图2 前围板声源腔和接收腔示意图Fig.2 Source and receive cavities diagram of dash

2 Kriging模型建立

2.1 试验设计

最优拉丁超立方试验设计使所有的试验点尽量均匀的分布在设计空间，具有非常好的空间填充性和均衡性。图3(a)显示了拉丁超立方随机生成的试验点分布，图3(b)显示了最优拉丁超立方生成的更加均匀的分布。

图3 随机拉丁超立方设计和最优拉丁超立方设计Fig.3 Latin hypercube and optimal latin hypercube

从图3可知，最优拉丁超立方设计不仅具有随机拉丁超立方空间填充能力强，拟合非线性响应精度高等优点，同时还使得试验点在空间分布均匀。此外，该试验设计方法适用于Kriging响应面建立[3]，因此选取最优拉丁超立方试验设计方法来生成样本点。

本文以某汽车前围的声学包作为研究对象，其声学包组成为吸声材料PU泡沫和隔声材料EVA的组合，其中EVA为等厚结构，主要是改变其面密度来获取不同的隔声量，PU泡沫主要是改变其厚度来改变其吸声效果。因此选取EVA面密度及PU泡沫厚度为其中两个设计变量。此外，由于汽车前围声学包的覆盖率和各种过孔的堵件厚度不同，都会影响前围子系统的隔声效果，因此同时选取覆盖率和堵件厚度作为设计变量。

由于吸隔声材料的厚度对车内噪声影响较大，一般厚度越大，结构的吸隔声性能越好。但是受到实际车辆的空间布置限制，设置PU泡沫厚度的上限为25 mm，下限为10 mm。针对市场上EVA材料的面密度调查，设置它的变化范围为2～7 kg/m2。同样考虑到PU发泡和EVA组合声学包的实际安装问题，将覆盖率上限设置95%，下限设置为80%。针对前围过孔堵件，选取不同厚度的硬橡胶，并设置橡胶堵件厚度的变化范围为1.5～3.5 mm。此外，选取PU泡沫的密度为110 kg/m3，EVA的厚度为3.5 mm。

采用最优拉丁超立方方法生成36组试验点，针对每组试验点可用前围SEA模型计算出传递损失随频率的变化曲线及声学包的总重量，其中第一组的结果如图4所示。

图4 第一组试验点隔声量Fig.4 TL of the first test point

在共振频率之后吻合频率之前声传递损失处于质量控制区，在该频率范围内声传递损失与频率成明显的线性关系。因此在声学包装前期开发的时候，可以用平均隔声量定量地分析声学包的隔声性能而忽略不同频率下人耳听觉主观感受及评价的差异。据此可以得到所有试验点的平均隔声量及声学包总重量如表2所示。此外，利用最优拉丁超立方随机生成另外10组试验点，用于验证近似模型。

表2 最优拉丁超立方生成的36组样本点Tab.2 36 test points generated by latin hypercube

2.2 kriging建模方法与验证

为了得到覆盖率、EVA面密度、PU泡沫厚度、堵件厚度四个输入变量与平均隔声量和总重量两个输出变量之间的量化关系，提高优化效率，须分别建立以声学包平均隔声量和总重量为响应的近似模型。因Kriging模型是一种估计方差最小的无偏估计模型[4]，此外它可以覆盖所有的样本点，近似面质量较高[5]，故可采用该方法来建立近似模型。

ISIGHT软件提供了拟合Kriging模型的两个流程[6]，分别为相关参数拟合流程和Kriging模型拟合流程。其中根据相关参数拟合流程得到的各响应中与各设计变量对应的参数θ将被用在Kriging模型拟合流程中，从而得到各响应的Kriging代理模型表达式[7]。其中声学包隔声量TL的Kriging替代模型与EVA面密度、覆盖率、泄露之间的响应关系如图5所示，颜色越深的区域响应越大。

表3 用于验证近似模型可信度的试验点Tab.3 The test points used to verify the approximation model

由图5可知，声学包的隔声量受覆盖率、堵件厚度、PU泡沫厚度及EVA面密度的影响较大，而且覆盖率越大，PU泡沫厚度越大，堵件厚度越大、EVA面密度越大皆会使得TL越大。反之，声学包隔声量越小。该响应关系与实际相吻合，初步验证了近似模型的正确性。同理也可得到声学包重量与四个自变量之间的响应关系。

通常为了检测近似模型的拟合精度，常采用R2来度量。R2的定义如下式：

(1)

图5 声学包的Kriging近似模型Fig.5 Kriging model of sound package

3 声学包的多目标优化

声学包在优化的过程中不仅要考虑到隔声量也要顾及其成本、重量等因素，往往这些因素之间是相互冲突的，即通过增加声学包材料厚度或者面密度可以增加隔声量，但这又会引起重量的增加，不利于声学包的轻量化设计；反之，则会引起声学包的隔声量下降。要获得声学包隔声性能和重量的最优解，其必须同时满足以下两个条件：

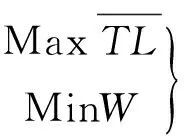
(2)

多目标优化问题的优化解不是唯一解而是一个解集，即Pareto最优解集。Pareto最优解之间不存在支配关系，提高其在任何一个目标上的性能，必然会引起在其它目标上的性能降低[9]。通常求解多目标优化问题有非归一化和归一化求解方法，因归一化求解方法需要优化者主观的赋予每个目标函数一定的权重，这可能导致求解结果的可信度降低。此外，归一化方法对于Pareto最优前沿的形状很敏感，不能处理Pareto前沿的凹部[10]。因此优先考虑非归一化求解方法。非归一化方法能够使所求解集的前沿与Pareto 前沿尽量接近，并尽量均匀覆盖Pareto 前沿。目前，非归一化方法中的代表方法是：多目标遗传算法(Multi-Objective Genetic Algorithm,MOGA)，eArtius公司的ParetoExplorer方法等。

第二代非劣排序遗传算法NSGA-Ⅱ属于多目标遗传算法。它是在NSGA的基础上引入了精英策略，提高了算法的运算速度和鲁棒性，并保证了非劣最优解的均匀分布。因隔声量和重量之间的数量级不一样，若采用二进制编码，染色体长度聚增；若采用实数编码，计算精度收到限制[11]。因此在进行遗传算子之前须对其进行同级化处理，同级化方法为：

(3)

式中:TLmax，TLmin分别为隔声量的最大值和最小值；Wmax，Wmin分别为声学包重量的最大值和最小值。

采用ISIGHT中的Optimization模块并选择NSGA-Ⅱ算法求解，迭代800步之后，在以声学包隔声量最大及重量最小为目标的要求下，得到了声学包隔声量与总重量之间的Pareto图，如图6所示。

图6 平均隔声量和总重量之间的Pareto解集Fig.6 Pareto set of average insulation and weight

在图6中，正方形的点表示Pareto最优解，所有正方形的点构成了Pareto最优解集，三角形的点表示在声学包隔声量和总重量权重均为1时所得到的最优解。同时获得了该情况下覆盖率、橡胶堵件厚度、PU泡沫厚度及EVA面密度的最优值，其最优值分别为91.07%，3.34 mm，17.10 mm，2.49 kg/m2，此时得到声学包平均隔声量值为39.878 dB，总重量值为4.320 kg。

利用上述覆盖率、橡胶堵件厚度、PU泡沫厚度及EVA面密度参数重新设置SEA模型，得到了该参数下的计算结果并与优化预测的结果作比较，如表4所示。

从表4可以看出，声学包平均隔声量及总重量两项指标的偏差均较小，并且在5%以内，再次说明了Kriging近似模型拟合效果好，结果可信度高。该优化方法对声学包的设计具有一定的应用价值。

表4 SEA计算结果与优化后结果对比Tab.4 Comparison between SEA and optimal result

为了直观清楚的说明声学包隔声性能提高及总重量减小的效果，在满足声学包隔声量和重量权重相等的要求内任取三组试验点，如表5所示。通过重新设置前围板的SEA模型参数再次计算，将计算结果与本次实验求得的最优参数值作对比。

表5 试验点及最优值参数表Tab.5 Parameters of test points and optimal value

由图7可知，与试验点1相比较，其隔声量在400～10 000 Hz频率范围内明显低于最优参数对应的隔声量，且其总重量仅减0.46%。试验点2隔声量比最优参数对应的隔声量在400～10 000 Hz频率范围内相差无几，平均隔声量前者比后者高出1.28%，其总重量为5.808 kg，增幅为32.33%。可见重量增加较多才换取隔声量的微量增加。试验点3的隔声量在600～10 000 Hz频率范围内较最优参数对应的隔声量小，此外，其重量反而增加32.92%，这是参数匹配不恰当所导致的。

图7 三组试验与最优参数隔声量Fig.7 TL of three test points and the optimal value’s parameter

4 整车验证分析

为了检验上述方法的实际效果，验证该方法的可行性和有效性，可将上述图7中四组试验点的TL曲线分别代入已经通过对标试验验证了的整车模型中[12]。采用基于能量的隔声量试验技术(Power Based Noise Reduction, PBNR)，PBNR定义为点声源的声功率与某点测量的声压平方的比值，是1/3倍频程频率的函数，用对数的形式可以表示为:

(4)

p·p*为声压的均方值，或者所测量得到的声压自普；p*为声压p的共轭；Ⅱ为点声源在自由场测得的声功率。

在驾驶员头部声腔加载0.1 mw的声功率，获得发动机舱声腔的响应，从而得到如图8所示的PBNR。

图8 驾驶员头部声腔到发动机声腔PBNRFig.8 PBNR from driver’s headcavity to engine cavity

从PBNR的验证结果可以看出，该结果与四组试验点在前围中得到的隔声量-频率曲线相吻合，optimal仍然为最优值，从而验证了该方法的正确性。为了在整车里对比不同试验点所对应的驾驶员声腔声压级，设定了三档发动机转速分别为2 500 r/min和4 000 r/min两种工况，在半消声室里分别测得外部声腔的声压级作为约束声压加载到整车SEA模型上，分别得到如图9所示结果。

图9 不同工况下驾驶员头部声腔声压级Fig.9 Driver’s head cavity SPL of different loads

由图9可知，optimal试验点对应的驾驶员声腔声压级在400～8 000 Hz范围内都比试验点1要低。与试验点2相比驾驶员声腔声压级相差无几，试验点2对应的声学包重量反而增加许多。从上述分析可知，优化所得的参数是在覆盖率、EVA面密度、橡胶堵件厚度、PU泡沫厚度设计范围内兼顾隔声量和重量取得的最理想的结果。因此，采用NSGA-Ⅱ算法计算出的声学包最优参数可信度较高，其在隔声性能和总重量之间取得了最佳的平衡。

5 结 论

本文针对汽车前围隔声性能及声学包重量影响较大的四个因素为设计变量，根据实际安装及市场情况合理设定四个因素的变化范围，采用最优拉丁超立方试验设计方法生成空间分布均匀的36个样本点，对这36个样本点分别计算出其平均隔声量及声学包的总重量。利用样本点建立起Kriging模型并用另外的10个样本点验证近似模型的准确性。最后建立了以声学包平均隔声量及总重量为目标的多目标优化问题，通过优化计算得到覆盖率、橡胶条厚度、PU泡沫及EVA面密度的最优值。此后通过选取三组试验点验证该结果的正确性。该优化方法及过程对声学包的设计与研究有一定的指导意义与应用价值。

[1] 卢兆刚. 基于混合FE-SEA方法的汽车薄壁件中频声学特性预测及优化研究[D]. 杭州：浙江大学，2011.

[2] 于学华，张家栋. 汽车车内噪声产生机理及控制技术[J].噪声与振动控制，2008, 28(5)：122-125.

YU Xuehua, ZHANG Jiadong. Mechanism of inner noise generation of automobiles and the methods of control[J]. Noise and Vibration Control, 2008, 5(10)：14-20.

[3] 张冬冬，郭勤涛. Kriging响应面代理模型在有限元模型确认中的应用[J].振动与冲击，2013,32(9):187-204. ZHANG Dongdong, GUO Qintao. Application of Kriging response surface in finite element model validation [J]. Journal of Vibration and Shock, 2013, 32(9):187-204.

[4] 容江磊，谷正气，杨易，等. 基于Kriging模型的跑车尾翼断面形状的气动优化[J]. 中国机械工程，2010,22(2):243-246. RONG Jianglei，GU Zhengqi, YANG Yi, et al. Aerodynamic optimization of the cross section shape for a sports car rear wing based on Kriging surrogate model [J]. China Mechanical Engineering, 2010, 22(2):243-246.

[5] 杨晓涛，谷正气，杨振东,等. 汽车乘员舱多层吸声材料的多目标优化[J].振动与冲击，2013,32(4):21-25. YANG Xiaotao, GU Zhengqi, YANG Zhendong, et al. Multi-target optimization of multilayer sound absorption material combinations in passenger compartment of a car [J]. Journal of Vibration and Shock, 2013, 32(4):21-25.

[6] Engineous software ISIGHT 9.0 reference guide [M]. Engineous Software Inc., 2004.

[7] 高云凯，孙芳，余海燕. 基于Kriging模型的车身耐撞性优化设计[J].汽车工程，2010,31(1)：19-20. GAO Yunkai, SUN Fang, YU Haiyan. Crashworthiness optimization of car body based on Kriging surrogate model [J]. Automotive Engineering, 2010,31(1)：19-20.

[8] 陈则尧，吴宪，丁巨岳. 基于响应面法的汽车前防撞梁轻量化分析[J].计算机辅助工程，2014,23(3):16-20. CHEN Zeyao, WU Xian, DING Juyue. Lightweight analysis of front bumper beam based on response surface method [J]. Computer Aided Engineering, 2014, 23(3):16-20.

[9] 陈国栋. 基于代理模型的多目标优化方法及其在车身设计中的应用[D].湖南：湖南大学，2012.

[10] 徐磊. 基于遗传算法的多目标优化问题的研究与应用[D].湖南:中南大学，2007.

[11] 段绪伟，李以农，郑玲,等. 基于NSGA-Ⅱ遗传算法的磁流变悬置多目标优化[J].振动与冲击，2014,33(3):191-196. DUAN Xuwei, LI Yinong, ZHENG Ling, et al. Multi-objective optimization for a MR engine mount based on NSGA-Ⅱ algorithm [J]. Journal of Vibration and Shock, 2014, 33(3):191-196.

[12] SHAO Jianwang, WU Xian, WEI Na, et al. Optimal design of vehicle dash and floor sound package based on statistical energy analysis[C]// Sae World Congress, 2014.

Dash sound package optimization based on Kriging model and NSGA-Ⅱ algorithm

WU Xian, WANG Cheng, SHAO Jianwang, DENG Guoming

(School of Automotive Studies, Tongji University, Shanghai 201804, China)

Taking advantage of the statistical energy analysis (SEA) method, a SEA model for vehicle dash to calculate the sound transmission loss (TL) was established. By using the optimal Latin hypercube method, 36 test points of the dash sound package were generated, based on four design variables in terms of coverage, blocking thickness of holes, PU foam thickness and EVA surface density as well as two optimization targets in terms of insulation performance and sound package weight. The TLs of different sound package schemes were calculated. Then the Kriging approximation model was built and also verified. The multi-objective optimizations of the insulation performance and the sound package weight were performed by appling NSGA-Ⅱ algorithm, and the Pareto optimal solution set was obtained. The optimal values of coverage，blocking thickness, PU foam thickness and EVA surface density were obtained, giving the same weight to the insulation performance and the sound package weight, and the results were verified by calculating at three randomly selected test points the TL, the power based noise reduction (PBNR) in the whole vehicle and the sound pressure level (SPL) on the driver’s head. The results show that the best balance between the insulation performance and the weight of dash sound package can be acquired in accordance with the optimal values.

sound package optimization; optimal Latin hypercube; Kriging model; NSGA-Ⅱ algorithm

留学回国人员科研启动基金项目，教外司留[2015]1098号

2015-08-07 修改稿收到日期：2015-10-24

吴宪 男，博士，副研究员，1971年10月生

邵建旺 男，博士，助理研究员，1984年7月生 E-mail:shaojianwang@tongji.edu.cn

U27；U46

A

10.13465/j.cnki.jvs.2016.22.034