含螺栓连接转子系统非线性振动特性研究

刘卓乾, 曹树谦, 郭虎伦， 李利青

(1.天津大学 力学系,天津 300072; 2.天津市非线性动力学与混沌控制重点实验室,天津 300072;3. 天津大学 内燃机燃烧学国家重点实验室，天津 300072)



含螺栓连接转子系统非线性振动特性研究

刘卓乾1,2,3, 曹树谦1,2,3, 郭虎伦1,2,3， 李利青1,2,3

(1.天津大学 力学系,天津 300072; 2.天津市非线性动力学与混沌控制重点实验室,天津 300072;3. 天津大学 内燃机燃烧学国家重点实验室，天津 300072)

针对航空发动机转子大量采用的螺栓法兰连接，建立了连接结构的力学模型，定性给出了两段转子在相对弯曲时连接部位弯矩的分段线性参数化模型。应用状态空间理论和数值计算方法对一个含螺栓连接的转子系统进行了数值模拟，研究其模态特性和稳态动力学响应。研究表明，分段线性变化连接刚度对中转速段尤其是二阶临界转速附近的模态和稳态动力学响应产生较大影响，而转子系统在低速段和高速段保持相对稳定的、可线性化的运动。分析了预紧力对转子运动特性的影响，发现预紧力对转子系统运动稳定性影响显著，在一定范围内增大预紧力会使系统不稳定加剧，但会缩短不稳定运动的区间范围。

转子系统；螺栓连接；稳定性；非线性动力学

航空发动机转子的连接结构可分为拉杆连接、螺栓连接和无螺栓连接三种形式。现代航空发动机连接结构的选用考证多种因素，除了保证转子段间较好的一致性和振动稳定性，为了满足推重比要求，对于质量的要求逐渐苛刻。螺栓连接结构简单，连接稳定性较好，较为轻便，因此广泛应用于航空发动机中[1-2]。

由于螺栓法兰连接本身的结构特性，航空发动机转子系统存在“准刚性”特性。即除去刚性转子应有的俯仰、平移振动外，实验中在某些特殊的转速下会发生错动和弯曲，甚至两段转子相位上的不一致。而螺栓连接的刚度小于转子的刚度，这使得螺栓连接成为故障发生的源头之一。

压气机转子典型的螺栓连接结构如图1所示，其各方向力学特性均可用分段线性刚度描述。BÖSWALD等[3-4]采用实验与数值方法研究了螺栓连接轴向和横向分段线性刚度的定性规律，提出了采用非线性传递函数方法识别横向刚度的途径。GAO等[5-6]用有限元法给出了拉杆转子连接的数学模型，并将其数学模型应用于Jeffcott转子，研究其动力学响应特性和模态特性。QIN等[7]用有限元法计算了螺栓毂筒连接的弯矩模型，给出了含弯矩模型的动力学响应特性。LIU等[8]结合有限元仿真和实验，对螺栓法兰连接的横向刚度模型进行了对比研究，发现了刚度模型随连接结构特性变化的一系列规律。

图1 压气机转子螺栓连接结构Fig.1 Bolt joint structure of aero-engines

国内外学者对于航空发动机螺栓连接结构的研究，着重于静态实验研究或者有限元仿真计算，动力学数值仿真分析的研究相对较少。对于螺栓预紧力的研究给出了一些规律，但对动力学响应的影响研究较少。本文通过建立一个简单的转子连接模型，突出螺栓法兰连接对于转子系统的动力学特性影响，研究螺栓连接对转子系统模态和非线性响应特性的影响。

1 转子螺栓法兰连接等效力学模型

为使相连的两段转子具有较好的转动同步性以及保持足够大的径向以及轴向刚度，连接结构在三维平动方向上对两段转子提供相对约束，还具有抵抗连接的两段转子弯曲的作用。

1.1 螺栓法兰连接的轴向力学特性

考虑一个螺栓法兰连接的简化模型，其剖面图如图2(a)所示。连接结构轴向力简化为两类，即弹性力和阻尼力，并认为其作用在一直条线上。

图2 螺栓法兰连接轴向力简化模型 Fig.2 Qualitative relationship between axial force and the relative displacement z

由于连接结构螺栓受拉而法兰盘受压，因此其轴向的弹性作用力存在着拉压不同的特性，定性函数如图2(b)中虚线所示。工程中需要在螺栓连接部位施加一个轴向预紧力，以使连接部分的力学特性相对合理。预紧力过大会减小结构寿命，过小会使得结构相对运动超过标准，因此通常以图中实线所代表的定性函数关系作为轴向弹性力，其中拉力的第二段刚度kT2=kc。简化成力学模型得到分段线性刚度，在图2(a)中用非线性弹簧表示。

1.2 螺栓法兰连接的弯矩特性

图2(a)所示的单个螺栓轴向力简化模型代表螺栓法兰连接的单个螺栓剖面。一个有n个性质相同螺栓的连接结构具有n个如图剖面。假设转子弯曲量较小，则在截面上一周的n个螺栓连接结构受拉和受压的连接区域数目相等，如图3(a)所示。图3(b)给出了由瞬时对称位置固定坐标系中两个螺栓组成的转子连接结构剖面图。

图3 连接部位弯矩模型示意图Fig.3 Model of the joint moment

左盘上下两点受力方向相反，使连接部位产生弯矩作用。若连接结构系统受力处于瞬时平衡，则有上下两点受力关系[9]:

(1)

式中：FTi为受拉端产生的拉力，FCi为受压端产生的压力，d为螺栓法兰连接的有效直径。共有n/2个图3(b)所示截面，产生n/2个弯矩。对于整个连接截面有:

(2)

航空发动机转子为准刚性转子，其涡动与横向振动均不明显。为了研究方便，把转子连接部分受到的合弯矩分解到绕x轴和y轴两个方向：

M=Mx+My

(3)

考虑绕x轴方向的弯矩示意图如图3(b)，则轴向力学特性使得连接结构拉压变形并不相等，分别为:

(4)

(5)

式中：kT、kC分别为螺栓连接的等效轴向拉压刚度。在小变形条件下，连接结构绕x轴转角与轴向变形的关系可以表示为:

(6)

将式(4)、式(5)代入式(6)，整理得到螺栓连接弯曲角刚度表达式：

(7)

由于预紧力存在，等效拉伸刚度kT呈现分段线性规律，对应的kθ也呈现分段线性规律，如图3(c)所示，与文献[10]分析定性一致。由于每个螺栓性质相同，则绕y轴弯矩模型可由同样过程获得，分段的临界点对应的相对临界转角:

(8)

式中：Fpre为等效预紧力。

由上述分析可知，转子系统发生弯曲的瞬时，连接部位的弯矩模型可由绕x、y轴作用的分段线性角刚度描述，沿连接截面一周的螺栓与固定坐标的四个交点为等效预紧力作用点。

1.3 含螺栓法兰连接的转子系统动力学建模

为了研究螺栓法兰连接结构对转子系统动力学的影响，基于下面假设建立转子系统的动力学模型：

(1) 为体现连接部分的刚度对转子系统的影响，将转子轴考虑为刚性轴，支撑采用刚性支撑结构；

(2) 将高低压叶盘简化为两个不同质量的刚性盘。转子系统的轴承支撑简化为简支约束。忽略弹性法兰盘的质量，连接结构的作用力看作两叶盘的直接相互作用力；

(3) 两段转子之间的约束弯矩简化为角刚度作用下，两盘相互的耦合弯矩作用；

(4) 假设转子横向振动较小，螺栓约束转子横向振动的刚度简化为线性刚度与线性阻尼；

(5) 忽略转子轴向运动。

根据上述假设得到含螺栓连接假设(4)自由度转子动力学模型如图4所示，其广义坐标为:

q=[θx1θy1θx2θy2]T

(9)

式中：θxi、θyi为别为两段转子刚体绕固定坐标系中x、y坐标轴的转角，i=1,2。

图4 含螺栓连接的转子系统模型示意图Fig.4 Model of the rotor system with bolt joints

这里需要说明，根据转子动力学建模理论，每个刚性转子运动需要用4个自由度表征，即xi、yi、θxi和θyi。单独讨论盘1的y方向，当盘1在y方向上的位移足够小时，此时刚体绕固定坐标轴x的转角也足够小,满足sinθ≈θ,此时y1=l1θx1。同理，x1、x2、y2也可由θy1、θy2、θx2表示。由于假设(1)，每盘运动使用两个自由度即可表征。

采用拉格朗日能量法建立4个自由度的动力学微分方程：

(10)

式中:K为线性刚度矩阵。根据假设(5)，线刚度kl取定值。本文建模认为转子系统为对称系统，即两段转子x、y平动方向的刚度作用相等，取klx=kly=kl。同理，由clx=cly=cl组成阻尼矩阵C。G为陀螺矩阵，表示陀螺效应力对系统的影响。

角刚度取分段线性模型，绕x轴旋转与绕y轴旋转产生的角刚度相等，kθx=kθy=kθ(Δθ),其规律满足如图6的定性关系。微分方程(10)中的非线性刚度矩阵:

Knl(Δθ)=

(11)

式中：Δθx=θx1-θx2，Δθy=θy1-θy2，即非线性刚度矩阵Knl(Δθ)随着系统的运动而变化。

2 含螺栓法兰连接转子系统的模态分析

2.1 螺栓法兰连接对转子涡动频率的影响

由于陀螺效应的存在，随着转速增高涡动频率逐渐分离，转子系统发生涡动。求解动力学微分方程(10)的特征值问题，通过将物理坐标转化为状态坐标，可以得到状态坐标式:

(12)

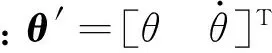
设式(12)的特解为q′=ψeλt，ψ为幅值列阵，将q′代入式(12)得到广义特征值问题:

λPq′+Qq′=0

(13)

变形为:

Hq′=λq′

(14)

式中：

计算矩阵H的特征值与特征向量可得到转子系统的n阶涡动频率[11]。系统的参数取值如表1所示。

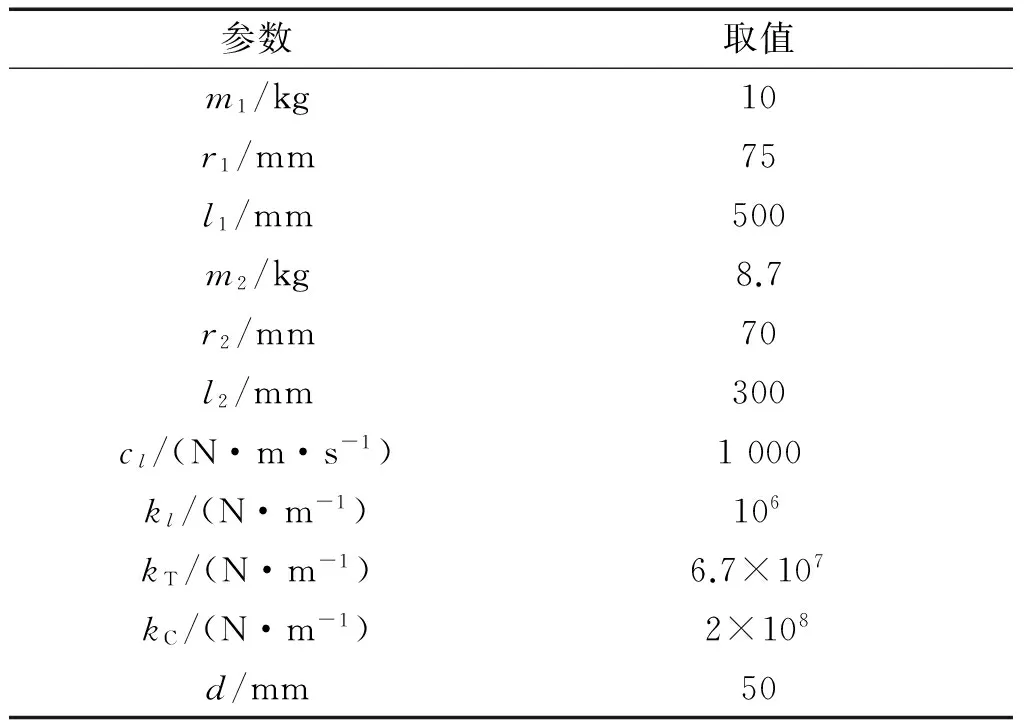
表1 转子系统简化模型的参数Tab.1 Parameters of the rotor system

需要指出，由于阻尼力只在转子系统不平衡响应中起到作用，在计算涡动频率随转速变化的过程中不考虑。由于状态空间理论只适用线性系统，角刚度矩阵Knl中的组成元素先后取角刚度分段的kθ1、kθ2形成两个线性系统，来分别计算弯矩呈分段线性变化前后系统涡动频率的值，对应等效预紧力Fpre取足够大和取0的两个极端值时系统的涡动频率。以此线性化过程，得出一个范围来定性预测涡动频率的变化区间，并认为非线性刚度对应系统的实际情况在这个区间内。使转子转速由0增长到1 800 rad/s，计算每个转速下对应H矩阵的特征值问题，将各阶特征值取虚部得到对应该转速下的涡动频率，绘制坎贝尔图如图5所示。

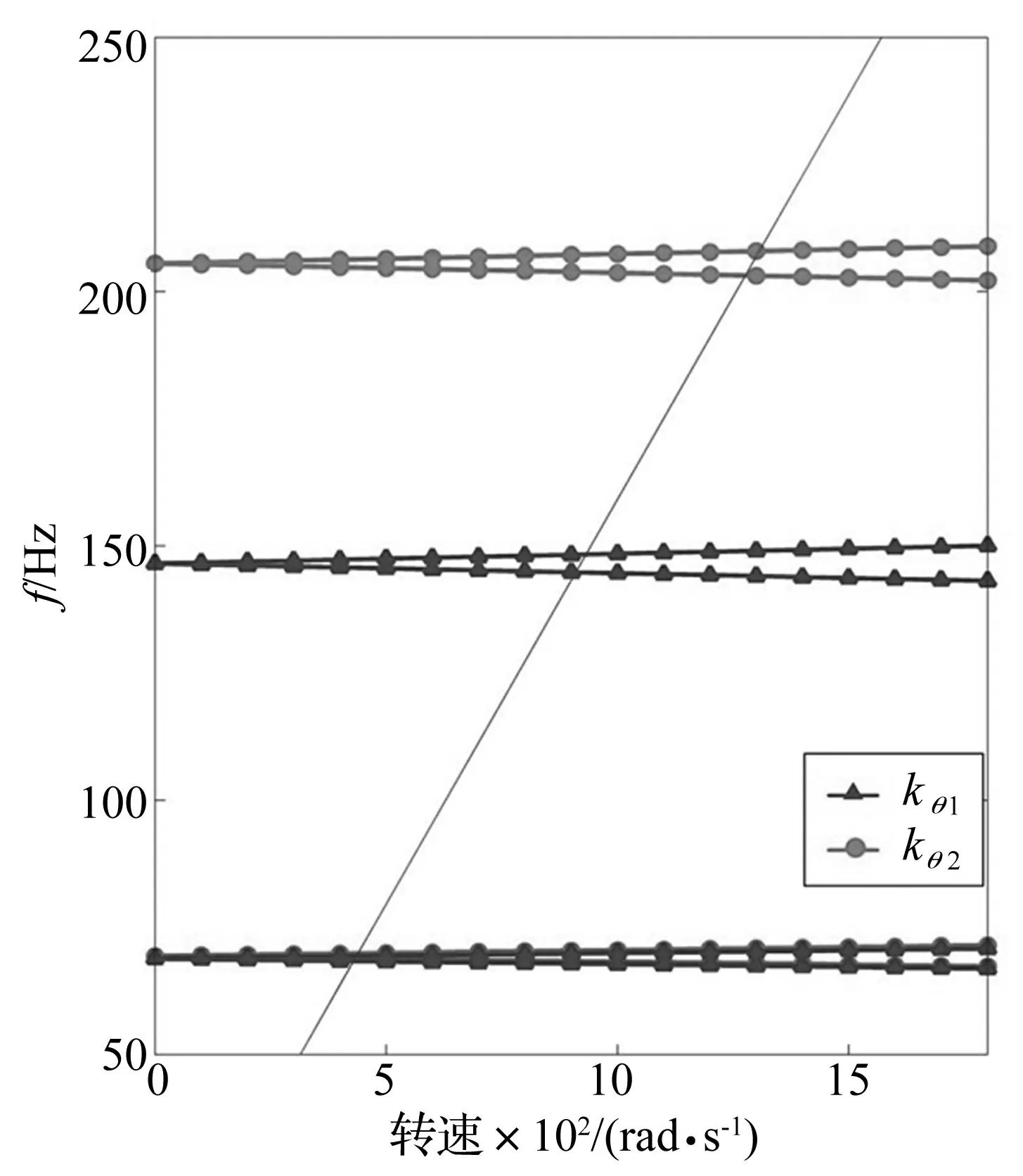
图5 含螺栓连接转子系统的坎贝尔图Fig.5 Campbell diagram of the rotor system with bolt joints

图5中斜线与频率曲线的交点其横坐标为临界转速。可以看出，角刚度取不同值时，第一阶涡动频率差异并不明显，而第二阶产生了较大差异。角刚度取kθ1时，系统的第二阶涡动频率较小；而角刚度取kθ2时系统第二阶涡动频率较大。第一阶临界转速没有明显差异，为445 rad/s；由于两线性系统第二阶涡动频率的差异，临界转速也产生了较大的差异，分别为910 rad/s与1 320 rad/s。可以发现角刚度取分段线性时，第一阶临界转速不会受到角刚度变化的太大影响，而第二阶临界转速出现较大差异，其取值在两个线性系统计算的两个临界转速之间。可以发现系统的涡动并不明显，涡动频率的分离较小。这是由于两盘间的约束刚度足够大，转轴也简化为刚性所导致；同时刚性盘的质量取值较小，因此陀螺效应对于系统固有频率的扰动较小，反映在图5中就表现出无论角刚度取值如何，系统的涡动频率随转速升高分离不明显。这与实际发动机转子系统的短粗结构和准刚性特性一致。

2.2 含螺栓法兰连接转子的振型

计算角刚度取kθ1时对应各个转速下H矩阵特征值问题，可以得到各阶特征向量，对应各个转速下的转子系统两盘形心的振型，如图6所示。

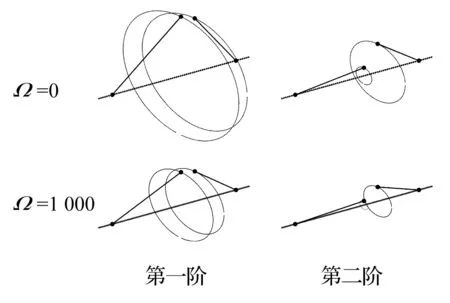
图6 静态与转速为1 000 rad/s的振型Fig.6 Modes of the rotor at static and 1 000 rad/s

对于图6结果需要指出，系统在静态时未发生频率分离，因此只有两阶振型；而在1 000 rad/s时转子系统涡动频率发生了分离，存在四阶振型，但由图5可知涡动频率分离程度并不明显，因此一二两阶、三四两阶振型十分接近，图6中仅给出两阶。通过图6中各盘的形心形成近似的圆形轨迹可以定性看出，转子系统x,y方向的振型基本一致。这是因为两盘间的约束在x和y以及绕x和y的方向上一致。从幅值来看，第一阶振型两盘幅值接近，第1盘略大于第2盘；第二阶时第2盘幅值明显大于第1盘，两盘发生错动。

3 含螺栓法兰连接的转子系统稳态不平衡响应

由上节分析可以看出，当角刚度值发生变化时，转子系统在第二阶临界转速附近涡动频率值不能确定，且两盘发生错动。本节引入转子偏心不平衡量，采用四阶Runge-Kutta方法求解方程组，对转子系统进行数值计算，研究其最大幅值、临界转速的变化规律以及稳态不平衡响应。

假设偏心在两叶盘上，偏心距ε1=ε2=0.000 2 m，且偏心相位一致。加入转子系统的不平衡激励后，动力学微分方程(10)变为:

(16)

式中：f(t)为离心力激励矩阵。

3.1 含螺栓法兰连接转子系统不平衡响应

取不同等效预紧力，以转速为分岔参数，从0逐渐升高到1 800 rad/s，取dθx1/dt=0截面作分岔图如图7(a)～(e)所示，并作出等效预紧力分别取5 kN、10 kN、20 kN和40 kN时局部转速范围内最大李雅普诺夫指数，如图7(b)～(e)中小图所示。

通过比较一系列分岔图可以看出，转子系统在第一阶临界转速附近运动没有明显变化，但过第二阶临界转速时发生分岔；随着Fpre增大，第二阶临界转速峰值逐渐不明显甚至发生突跳；临界转速值也从910 rad/s(Fpre=2 kN)逐渐升高到1 300 rad/s(Fpre=40 kN)左右，变化范围与图5给出的范围基本一致。

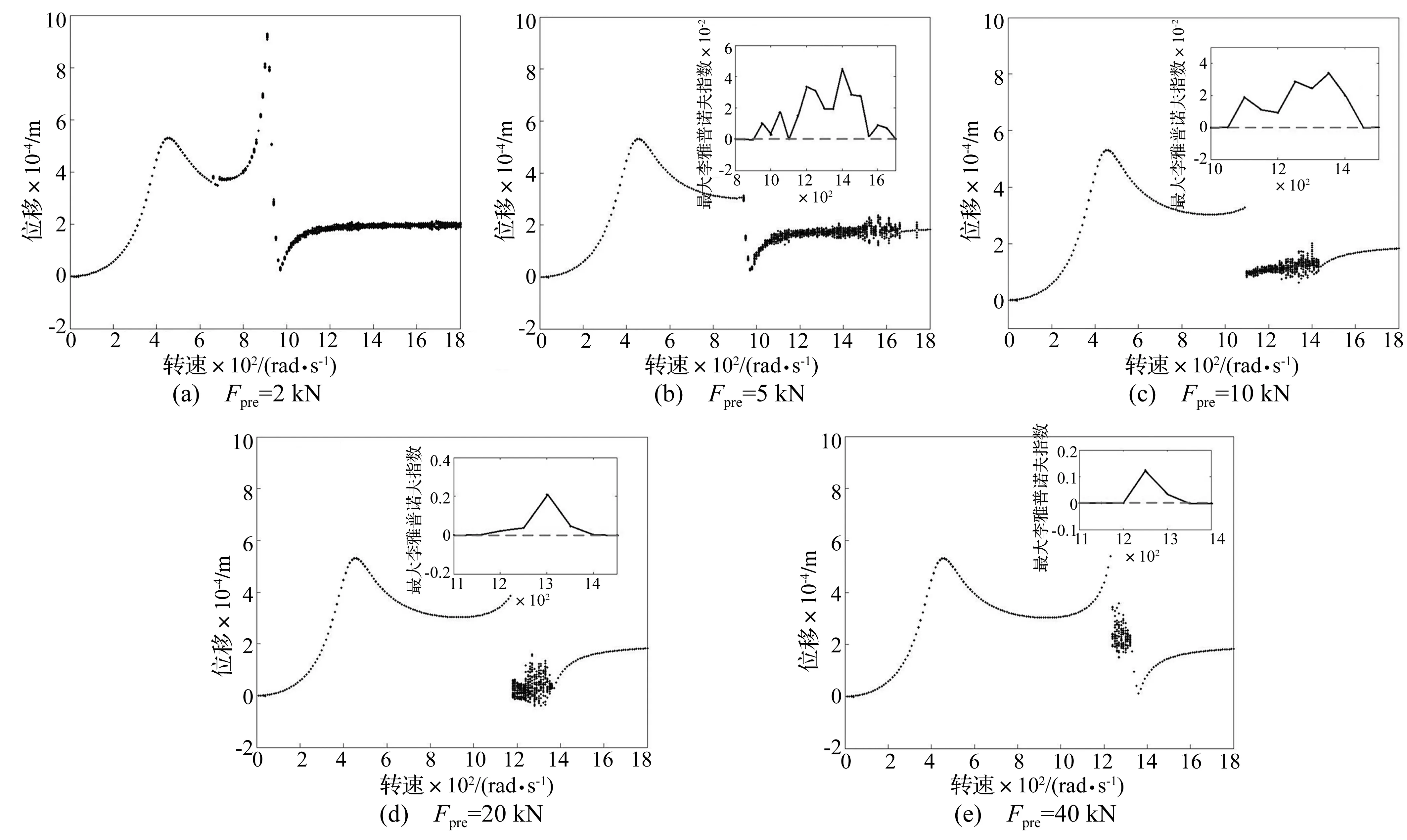
图7 不同等效预紧力Fpre下第1盘y方向位移分岔图Fig.7Bifurcationdiagramsofdisplacementsinthedirectionofyunderdifferentequivalentpre-tighteningforceFpre

Fpre取不同值时，系统位移响应总会在某一转速下发生突跳，与文献[6]的响应研究中在峰值附近发生的突跳类似；由图7(b)～(e)中的最大李雅普诺夫指数可以看出，转子系统在突跳点之后发生混沌运动，并且随着转速继续升高发生倒分岔变为周期运动。不同的Fpre取值其对应的岔点以及倒分岔点均不同。当Fpre取值增大时，其突跳点向高转速方向移动，而倒分岔点向低转速方向移动，分岔转速区间逐渐变小，如表2所示。

图8为当Fpre=10 kN、转速为1 200 rad/时盘1在y方向的稳态响应。从图7(c)以及图8(b)中可以看出，盘1在该转速下发生混沌运动；除两阶模态峰值外出现了3倍频，但幅值较小；转子的两个横向振动不再对称，转子此时运动轨迹变复杂。图9为Fpre=20 kN、转速为1 200 rad/s时盘1在y方向的稳态响应。对比图8可以看出，转子系统运动更加复杂，频谱图中3倍频幅值更高，且出现了5倍频；轴心轨迹也更加不规则。这表明等效预紧力不仅使得混沌运动的转速区间变小，而且使转子系统运动更加复杂。通过图7(c)和图7(d)的比较，可以看出Fpre=20 kN对应的最大李雅普诺夫指数高于Fpre=10 kN一个量级，其混沌运动更加无序。

表2 不同预紧力下运动特性比较Tab.2 Comparison of motion characteristics under different pre-tightening force Fpre

图8 Fpre=10 kN、1 200 rad/s时的稳态响应Fig.8 Steady response at 1 200 rad/s, Fpre=10 kN

图9 Fpre=20 kN、1 200 rad/s时的稳态响应Fig.9 Steady response at 1 200 rad/s, Fpre=20 kN

3.2 两盘的相对运动描述

转子受到不平衡激励后发生两盘的相对错动，螺栓法兰连接参数化模型中两盘相对转角存在一个临界值Δθ0，临界值两边系统的角刚度发生变化。由第2节内容可知，该临界转角的大小随等效预紧力变化。

图10 等效预紧力分别取2 kN、10 kN和20 kN时 不同转速下的相对转角Fig.10 Relatively rotation angle at diferent rotate speed when Fpre=2 kN、10 kN、20 kN

等效预紧力分别取2 kN、10 kN、20 kN，系统运动稳定后两盘相对转角如图10所示，图中双直线表示该等效预紧力下的相对临界转角。由于转子横向平动和弯曲存在关联，图中只给出了角度相对值。对比图7(a)、图7(c)和图7(d)可以发现，相对转角未超过临界值的转速下，盘1维持单周期运动；而当相对转角超过临界时，盘1发生混沌运动。可以认为分段线性角刚度发生变化是转子系统发生混沌运动的原因。比较图10(b)和图10(c)，Fpre=10 kN时转子系统稳定运动时每一个周期相对临界转角都超过临界值，而Fpre=20 kN存在某些周期未超过临界值的情况，这使得转子系统运动更加复杂。

3.3 含螺栓法兰连接转子系统的响应幅值

Fpre分别取0 kN、2 kN和预紧力足够大的极限状态作比较，在1 800 rad/s的范围内得到了盘1和盘2中心点的y方向幅频曲线，如图11所示。

图11 转子系统在不同Fpre时的幅频特性曲线Fig.11 Amplitude-frequency curve of rotor system under different Fprein direction y

比较Fpre=0、Fpre足够大两种极端情况，此时转子系统为线性系统，角刚度取值不变。两种状态下第一阶临界转速值(450 rad/s)重合，Fpre=0对应的响应曲线幅值稍大；第二阶临界转速发生了较大差异，Fpre=0时系统的二阶临界转速为910 rad/s，而Fpre取足够大时为1 320 rad/s，幅值Fpre=0对应的曲线较小，与图5一致。二阶临界转速变小与文献[7]得到的定性规律一致，但由于本文转子系统模型突出连接结构影响，角刚度变化时二阶临界转速发生的变化差异较大。

对比图11(a)、(b)可以发现，第一阶临界转速时，盘1较盘2的响应幅值大，而第二阶临界转速下盘2比盘1幅值大，与图6振型分析得到的定性规律一致。

对应图10(a)，由图11小图可知，Fpre=2 kN对应的响应幅值曲线在低转速阶段以及第一阶临界转速附近与Fpre足够大的曲线重合，此时两转子的相对转角未突破临界值；当相对转角开始超过临界值范围时，在特定的转速(700 rad/s)下幅值发生波动跳跃，最终与Fpre=0的响应幅值曲线重合。

令盘2偏心距ε2为0，逐步增大盘1的相对偏心距ε1，系统对应最大响应振幅如图12所示。可以看出系统振动能量集中在第二阶临界转速附近。联系非线性动力学理论，能量集中使得第二阶临界转速附近发生复杂运动；此时由于两盘较大的相对转角，非线性现象也趋于明显。

图12 不同偏心量两阶临界转速幅值比较Fig.12 Comparison of amplitude at critical rotation speed with different eccentricity quantity

4 结 论

本文在研究含螺栓法兰连接转子系统的振动机理过程中得出了以下结论:

(1)建立了刚性转子螺栓法兰连接作用弯矩的一个简单模型，通过推导得到了转子耦合弯矩模型，与之前学者得到的弯矩特性定性一致。

(2)应用状态空间理论计算了动力学系统的特征值问题，给出了系统在动静条件下的振型。发现转子涡动频率分离不明显，且耦合角刚度函数的不光滑使转子系统涡动频率变小，二阶临界转速值发生变化。定性给出了转子两阶振型两盘振动幅值之间的关系。

(3)研究了不同等效预紧力下含螺栓法兰连接模型的转子系统不平衡响应。转子相对弯曲较大时，系统振动响应发生突跳，之后表现为混沌运动；预紧力增大，则分岔点后移，倒分岔点前移，混沌运动对应的转速区间有变小趋势，第二阶临界转速由900 rad/s附近逐渐增加到1 300 rad/s；同时转子系统的运动不稳定加剧，混沌运动更加明显。

(4)在系统能量集中在第二阶临界转速附近，两盘响应幅值大小有明显差异。幅频特性曲线规律随着分段角刚度变化而发生变化，表现为低速段和高速段规律曲线不同的特性。

[1] 刘长福, 邓明. 航空发动机结构分析 [M].西安：西北工业大学出版社，2006.[2] 杨帆, 赵普扬, 葛长闯. 无螺栓高压压气机转子结构分析[J]. 航空发动机，2012,38(3): 42-45. YANG Fang, ZHAO Puyang, GE Changchuang. Structure analysis of no bolted high pressure compressor rotor[J]. Aeroengine, 2012,38(3): 42-45.

[3] BOESWALD M, LINK M. Experimental and analytical investigations of non-linear cylindrical casing joints using base excitation testing[C]// Proceedings of International Modal Analysis Conference.Kissimmee, FL:(IMAC-XXI), 2003.

[4] BOESWALD M, LINK M. Identification of non-linear joint parameters by using frequency response residuals[C]// Proceedings of the 2004 International Conference on Noise and Vibration Engineering. Leuven: ISMA, 2004.

[5] GAO J, YUAN Q, LI P, et al. Effects of bending moments and pretightening forces on the flexural stiffness of contact interfaces in rod-fastened rotors[J]. Journal of Engineering for Gas Turbines and Power,2012, 134(10): 102503-102510.

[6] YUAN Q, GAO J, LI P. Nonlinear dynamics of the rod-fastened jeffcott rotor[J]. Journal of Vibration and Acoustics, Transactions of the ASME,2014, 136: 021011.

[7] QIN Z Y, HAN Q K, CHU F L. Analytical model of bolted disk-drum joints and its application to dynamic analysis of jointed rotor[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(4): 646-663.

[8] LIU S G, MA Y H, ZHANG D Y, et al. Studies on dynamic characteristics of the joint in the aero-engine rotor system[J]. Mechanical Systems and Signal Processing, 2012, 29(5): 120-136.

[9] 栾宇.航天器结构中螺栓法兰连接的动力学建模方法研究[D]. 大连：大连理工大学，2012.

[10] 王建民，郑常良. 螺栓对接结构的非线性解析建模与分析[J].振动与冲击,2013,32(20): 5-8. WANG Jianmin, ZHENG Changliang. Nonlinear analytical modeling and analysis for bolted joint structures[J]. Journal of Vibration and Shock, 2013,32(20): 5-8.

[11] 曹树谦，张文德，萧龙翔.振动结构模态分析-理论实验与应用[M]. 天津：天津大学出版社，2014.

Vibration characteristics of rotor systems with bolt joints

LIU Zhuoqian1,2,3, CAO Shuqian1,2,3, GUO Hulun1,2,3, LI Liqing1,2,3

(1. Department of Mechanics, Tianjin University, Tianjin 300072, China;2. Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control, Tianjin 300072, China;3. State Key Laboratory of Engines, Tianjin University, Tianjin 300072, China)

Bolt joint structures are widely used in the aero-engine rotor systems. The mechanical model of a joint structure was set up and a parametric model for the bilinear moment distribution was given qualitatively. The modal characters and steady responses of the rotor system with bolt joint were investigated, by using the state space theory and numerical simulation. It is shown that the bilinear moment character has influence on modal characters and steady responses at medium rotational speed, especially at the vicinity of second order critical rotational speed, while it keeps steady and can be linearized at lower and higher rotational speeds. It is also found that pre-tightening force has a large influence on the stability of the rotor system. The increasing of pre-tightening force can intensify the instability of the system, but shorten the range of unstable motion.

rotor system; bolt joint; stability; nonlinear dynamics

国家973计划资助项目(2015CB057400)；天津市自然科学基金项目(11JCZDJC25400)

2015-07-02 修改稿收到日期：2015-09-13

刘卓乾 男，硕士生，1990年生

曹树谦 男，博士,教授,博士生导师，1964年生 E-mail: sqcao@tju.edu.cn

V231

A

10.13465/j.cnki.jvs.2016.22.002