基于EEMD分形与二次型SPWV分布的爆破振动信号分析

杨仁树，付晓强，张世平，苏 洪

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083； 2. 太原理工大学 矿业工程学院，太原 030024)



基于EEMD分形与二次型SPWV分布的爆破振动信号分析

杨仁树1，付晓强1，张世平2，苏 洪1

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083； 2. 太原理工大学 矿业工程学院，太原 030024)

通过EEMD(Ensemble Empirical Mode Decomposition)分解和分形盒维数组合算法，结合爆破振动信号统计自相似特性，提出了利用广义自相似性因子来识别爆破振动信号主分量的EEMD分形盒维数广义自相似性方法，并用机车运行振动信号对该方法的精确度进行了验证。将爆破振动原始信号和优势分量重组信号分别采用多重分形算法，定量描述了爆破振动信号在无标度区内的多重分形特征,并对比分析了原始信号和优势分量重组信号的Cohen类二次型SPWV(Smooth Pseudo Wigner-Ville)分布时频特性。结果表明：EEMD分形盒维数广义自相似性方法能够精确识别振动信号的主分量。EEMD优势分量重组多重分形与重组二次型SPWV分布相结合分析方法，可以深刻揭示爆破振动信号中包含的局部时频特性，更能有效改善模态混叠并消除交叉项干扰，提高信号时频聚集性。

爆破振动；EEMD分解；分形盒维度；SPWV分布

爆破振动信号分析，作为评价爆破效果的重要手段，其主要目的在于揭示爆破振动波形所包含的时频信息，以此来优化爆破参数、控制爆破产生的次生灾害，降低负面效应的危害程度。近几年来，国内外科研院所和理论学者，对爆破振动信号分析领域展开了更加深入的探讨和研究，取得了丰硕的成果。ALDAS等[1]提出了一种新的爆破减振分析方法，该方法不考虑任何爆破参数，而仅仅依靠选择合理的微差延期时间，可将爆破引起的地表振动降至原来的1/8。蔡宗义，王占江等[2]，对黄土中100 kgTNT当量地下封闭爆炸进行试验，采用Wigner-Ville分布对收集到的振动信号进行分析，揭示了其所包含的时频特征和能量分布情况，直观展示了爆破振动能量随时-频的变化规律。谢全民等[3]建立了爆破振动信号三维曲面分形盒维数模型，并修正了三维和二维分形盒维数之间的数值关系；赵明生等[4]利用小波、HHT分析中的EMD与EEMD对实测爆破振动信号进行低通去噪，通过对比验证了EEMD信号去噪的准确性；凌同华等[5]通过构造、添加自适应小波基， 精确识别了微差起爆延时间隔，收到了良好的应用效果。

不同的分析方法，有其独特的优势，但是由于爆破破坏机理的复杂性，导致对爆破振动效应的认识，还存在很多的缺陷和不足。本文利用HHT变换中的EEMD分量分形盒维数，优势分量重组多重分形和SPWV时频分布组合分析方法，对工程实测爆破振动信号进行了分析。试图来细化爆破振动信号所包含的时频特征，改善信号时-频-能分析精度，为爆破振动信号深层次分析建立新的理论依据。

1 信号EEMD分解理论

1.1 信号EEMD分解过程[6]

HHT(Hilbert-Huang Transform)变换中的经验模态分解EMD(Empirical Mode Decomposition)和白噪声聚类经验模态分解EEMD(Ensemble Empirical Mode Decomposition),是具有自适应性和精确辨识能力的信号处理方法。由于聚类经验模态分解EEMD克服了经验模态分解EMD容易产生模态混叠现象的缺陷，在非平稳信号分析中得到广泛应用。

通过给原始信号x(t)叠加不同的高斯白噪声信号ωi(t)，重新得到一总体信号X(t)：

X(t)=x(t)+ωi(t)

(1)

对X(t)进行EMD分解，得到各阶IMF(Intrinsic Mode Function)分量：

(2)

EEMD分解对信号X(t)所加高斯白噪声的次数服从如下统计规律：

(3)

式中：N为总体个数，ε为白噪声的幅度，εn为原始信号与最终IMF分量相加得到的信号之间的误差。最终原始信号x(t)被分解成:

(4)

聚类经验模态分解中IMF=EEMD(x(t),Nstd,Ne),其中x(t)为分析信号，Nstd指的是噪声方差，一般取值为：0.2～0.3，此处取值为0.2；Ne为噪声组数，就是运行次数，取值100。EEMD是在EMD的基础上添加不同的高斯噪声用来抵消原信号中的干扰成分，待处理信号不再是单纯的x(t)，所以分解后得到的本征模态函数IMF阶数更为细化。

1.2 信号EEMD分解

图1为从某一实测微差爆破振动信号分离出来的子信号速度-时程曲线。采样频率1 024 Hz，采样时间长度为0.898 s，具有爆破振动信号随机和非线性的典型特征。

图1 爆破振动子信号速度-时程曲线Fig.1 The velocity vs time curse of blasting vibration sub-signal

将图1中爆破振动信号按照上述步骤进行分解，得到12个IMF分量和一个周期趋于无穷的趋势项r。图2为图1原始信号及其EEMD分解得到的IMF分量及对应的频谱。

EEMD分解得到的各阶分量，可以很好展现出信号频谱特性。其中x为原始信号，IMF1分量为信号包含的白噪声,IMF2为信号的高频；分量IMF3、IMF4、IMF5、IMF6频率逐渐降低，说明在爆破振动波传播过程中高频已大幅衰减，但其振幅却较IMF2大幅增加，并包含了信号的大部分能量，属于信号的优势频带，应加以重点考虑；IMF7～IMF12为分解后频率更小的分量及信号的微弱变化，r为信号的趋势项。

2 盒维数广义自相似性方法确定信号主分量

2.1 分形盒维数

分形盒维数DB因其简单精确的数学计算和经验估计，是最常用的分形维数。爆破振动信号分形是振动波形复杂性和不规则形态的定量描述，爆破振动波形曲线包括纵向的振动幅值以及横向的时间效应两个尺度。波形覆盖网格的横向时间尺度δ1完全由信号的采样时间间隔Δt决定，而纵向尺度δ2与爆破振动波形振幅有关。

假定存在于二维平面R2内的爆破振动波形时程曲线L，设与曲线L相交的所有网格数量为Nδ1(或Nδ2)，则在矩形盒覆盖情况下的曲线L盒维数定义为[7-8]：

图2 爆破振动信号EEMD分解及频谱Fig.2 Blasting vibration signal EEMD decomposition and frequency spectrum或2)

(5)

爆破振动信号波形属于无规则非线性曲线，无法用函数准确描述。因此，只在其无标度区内才具有分形维数。Dδ1×δ2是通过在无标度区内由(log2(δi),-log2(Nδi)的拟合直线斜率来确定的,其中i=1或2。对于曲线的盒维数而言，他体现了曲线的复杂程度，其盒维数值是介于1～2[9]。

2.2 广义自相似性方法确定信号主分量

爆破振动信号是典型的广义自相似性信号，信号的“广义自相似性(Generalized Self-Similarity)”是指信号内在的一致性和外在形式的多样性。信号的广义自相似性是信号的分形特征，对信号的准确辨识起着决定性作用。

此处，定义广义自相似性因子ΔGSS为:

(6)

式中:i=1,2,…,n,i为信号最终分解数目，Di为信号分解的第i个IMF分量的分形盒维数值，Dx为分析的原始信号的分形盒维数值。ΔGSSi值越小，表明信号分量的广义自相似度越高，与原始信号的相关性也越强，反之，相关性越弱。

现对图2中各IMF分量进行分形盒维数计算，回归拟合统计类型采用最小二乘法。计算得到各EEMD分量的盒维数值分别为：D1=1.90、D2=1.84、D3=1.35、D4=1.62、D5=1.72、D6=1.73、D7=1.60、D8=1.44、D9=1.22、D10=1.07、D11=1.04、D12=1.03、Dr≈1。上述可以看出：趋势项r分形盒维数约为1，说明该分量已无明显分形特征。优势分量IMF3～IMF6分形盒维数值为1.35、1.62、1.72、1.73，反映出爆破振动信号多频段多振形的分形特征，该维数值范围分量可定量刻画信号的奇异场分布。因此，可确定信号优势分量盒维数值区间为1.3≤DB≤1.8。

计算图1中原始信号分形盒维数值为Dx=1.66，根据上述可知，与其广义自相似性最高的是IMF4分量(盒维数值为1.62，ΔGSS4=0.04)，可确定该分量为信号的主分量。

图3为图1中爆破振动信号IMF4分量、分形盒维数及增量双对数拟合曲线。图3(a)中IMF4分量清晰描述了微差爆破各段别雷管起爆波形的细观形态，这与实际中使用的雷管段别也是一致的。图3(b)中分形拟合曲线保持较好的线性递增，增量拟合曲线出现几处振荡，这是爆破振动信号各段雷管起爆产生冲击波相互作用的结果。

图3 爆破信号IMF4分量、分形盒维数及增量双对数坐标Fig.3 Blasting signal IMF4 component, the fractal box dimension and incremental double logarithmic coordinates

2.3 EEMD分形盒维数广义自相似性方法验证

为了验证EEMD分量分形盒维度广义自相似性方法在振动信号主分量识别中的准确性，对图4所示东方系列机车运行振动信号进行分析。机车运行振动信号经过EEMD分解，得到 12个分量及趋势项r。从各分量波形和频谱特征，确定IMF3～IMF7为信号的优势分量。

图4 机车振动子信号速度-时程曲线Fig.4 The velocity-time curve of locomotive vibration sub-signal

对13个分量进行分形盒维数计算，得到各分量盒维数值分别为：D1=1.91，D2=1.88，D3=1.47，D4=1.69，D5=1.76，D6=1.71，D7=1.62，D8=1.27，D9=1.13，D10=1.04，D11=1.02，D12=1.03，Dr≈1.02。计算图4中原始振动信号分形盒维数值为1.81，从分形盒维数值及广义自相似因子ΔGSSi值判断，IMF5分量(盒维数值为1.76，ΔGSS5=0.05)与原机车振动信号相似度最高，确定IMF5为图4机车振动信号主分量，这里对IMF5分量进行剖析。

图5 机车振动信号IMF5分量、分形盒维数及增量双对数坐标Fig.5 The locomotive vibration signal IMF5component, the fractal box dimension and incremental double logarithmic coordinates

图5(a)中，机车振动信号IMF5分量振速波形基本沿时间轴坐标0.6 s呈对称分布。0.35 s～0.82 s内共有3个自相似周期波形，可推断车轮转动周期T约为0.16 s。车轮直径D为0.91 m，转动一周距离l为2.857 m，每分钟转动375周，可知机车运行速度v为:

v=375×l×60=

375×2.857×60≈64.29 km/h

(7)

现场实测机车运行速度约为65 km/h，车速计算相对误差小于2%，完全满足工程实际分析的要求。因此，根据EEMD分形盒维数广义自相似性因子为标准来判断机车振动信号主分量是可行的。证实了EEMD分形盒维数广义自相似性方法确定振动信号主分量的高度可移植性。

3 优势分量重组多重分形与SPWV时频分析

3.1 优势分量重组多重分形

随着对数据分析的细化，研究人员发现有些看起来差异性较大的信号却具有十分接近甚至相同的分形盒维数(如上述2.3节中，图4中机车振动信号的IMF11分量与趋势项r具有相同的分形盒维数，但两者的波形上却有显著差异)。为了更精确提取信号波形所包含的信息，采用了多重分形理论，用多个标量指数的奇异测度组成的集合来客观描述分形体[10-11]。多重分形谱f(α)(奇异谱)，是描述多重分形最常用的一套参量。变量α称作奇异性指数或标度指数(hoelder exponents)，不同小区域可用不同的α来表征，具有相同α值的小区域构成一分形子集。由于小区域数目很大，因此可得到一组由不同α所组成的无穷序列构成的多重分形谱函数f(α)，不同的α对应的f(α)便构成了一个刻划多重分形性质的维数谱[12]。将图1中爆破振动信号EEMD分解得到的优势分量IMF3、IMF4、IMF5、IMF6

(1.3≤D≤1.8)重新合成，得到重组信号。图6分别是图1中原始信号和其优势分量重组信号的多重分形谱。

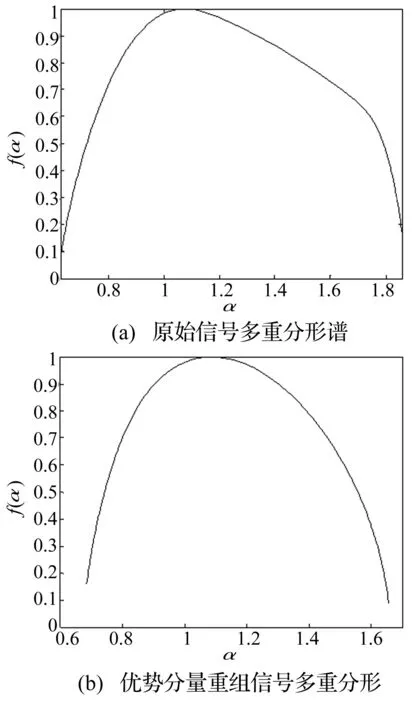
图6 原始信号多重分形谱及优势分量重组信号多重分形Fig.6 The original signals and advantages component restructuring multifractal spectrum

图6(a)中，爆破振动原始信号的多重分形奇异谱曲线ɑ的分布区间主要集中在[0.61,1.83]之间，区间差值Δα=αmax-αmin=1.22。说明原始信号奇异性指数变化范围较大，包含的频谱丰富，对于有效信息的识别有很大干扰。图6(b)中优势分量重组后的多重分形曲线是凸的，大体呈钟形分布,重组信号的脉动要平缓得多。ɑ的分布区间主要集中在[0.67,1.64]之间，区间差值Δα=αmax-αmin=0.97，奇异性指数分布范围比原始信号小，并且分形曲线更光滑均匀，表现出很高的标度不变性。说明EEMD优势分量重组多重分形更能表征信号的真实成分，过滤掉不相关项。从而缩小频谱范围，多重分形奇异谱曲线准确全面地反映了爆破振动信号奇异特征及分布特点。

3.2 优势分量重组二次型SPWV分布

对于给定的信号x(t)，定义平滑窗函数[13]：

(8)

平滑窗函数仅仅受短时窗函数h(t)的控制，为了在时域和频域独立控制平滑窗，平滑窗函数亦可定义为[14-15]：(t,f)=g(t)·H(-f)。利用此平滑窗函数可以修正Wigner-Ville分布定义得到平滑伪Wigner-Ville分布。平滑伪Wigner-Ville分布也可以用解析信号的频谱表示如下[16]：

(9)

式中:核函数为φ(τ,ν)=1,z(t)是被分析信号x(t)的解析信号,谱图是非负，实值的二次型分布[17-18]。图7和图8分别为图1爆破振动原始信号和其EEMD优势分量重组信号SPWV二次型时频分析。

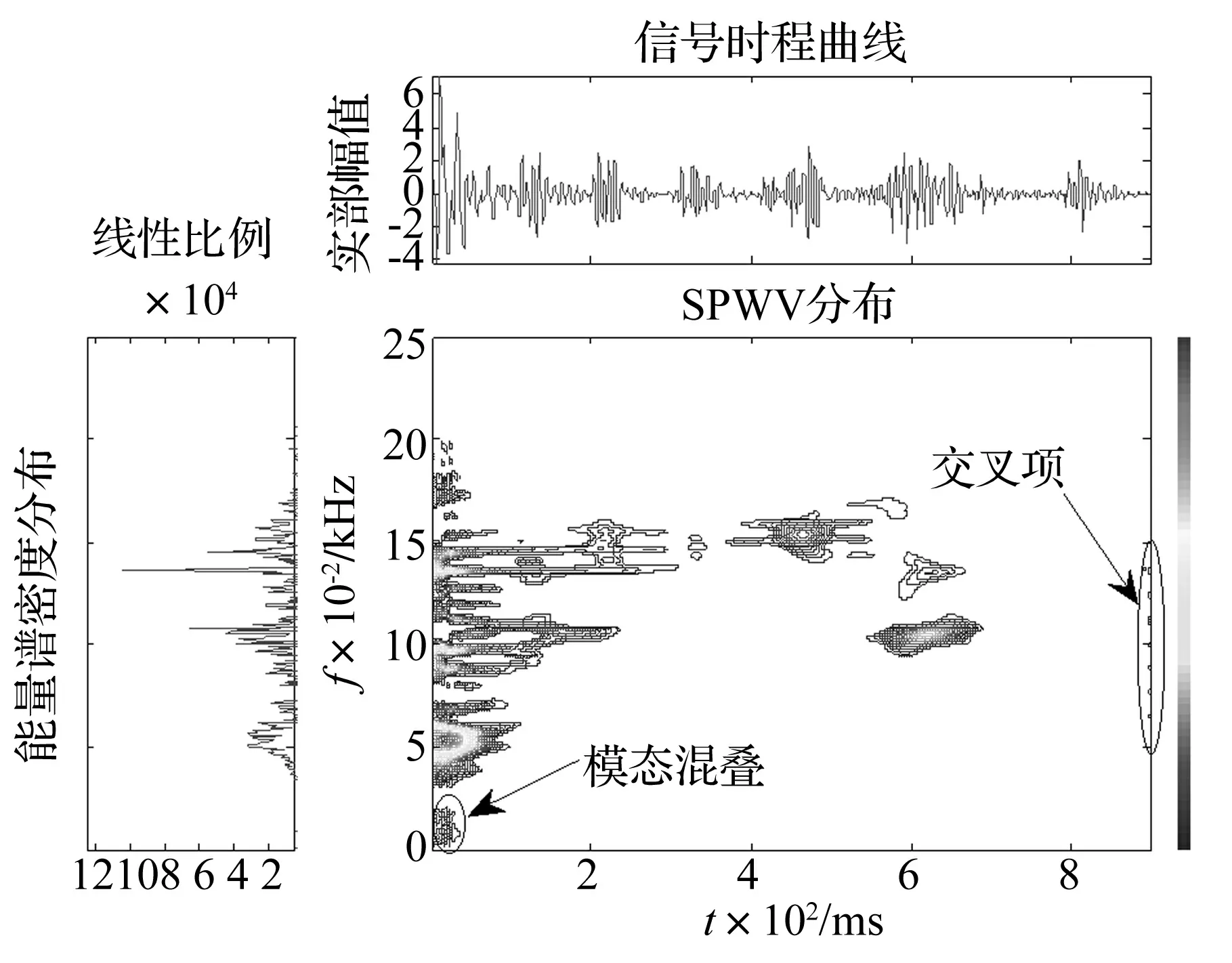
图7 原始信号SPWV能量等高线分布 Fig.7 Original signal SPWV contour energy distribution

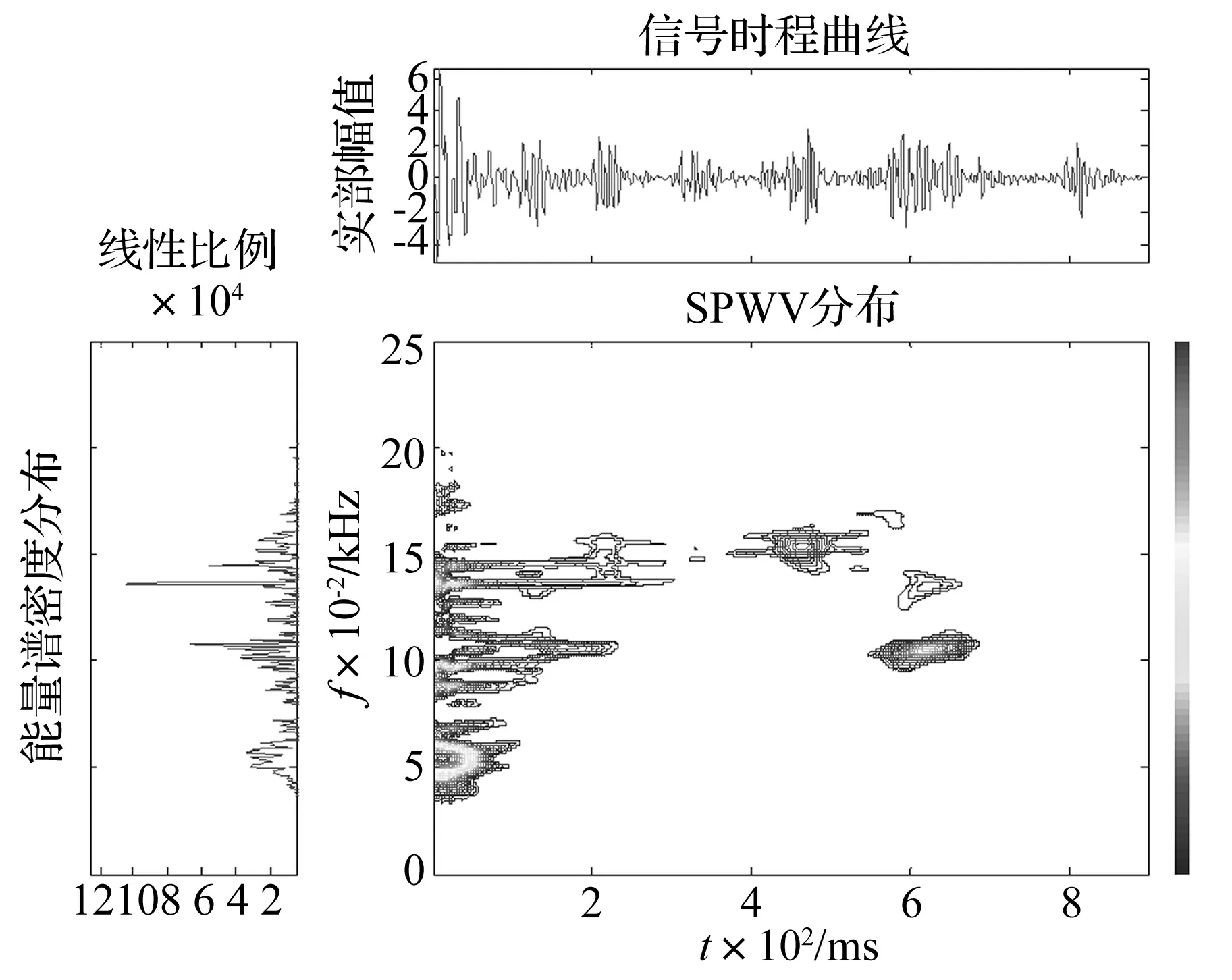
图8 优势分量重组SPWV能量等高线分布Fig.8 Advantage component restructuring SPWV contour energy distribution

考察时频分布性能的指标包括信号时频聚集性的改善和交叉项的减少。由图7和图8可知，由于WVD的双线性，使得信号能量分布出现了相干项。分形优势分量重组SPWV可以有效抑制交叉项，信号的时频局部聚集性较高，能有效识别出爆破振动多个优势主频带。精确获取爆破振动信号各频带主频率、能量时刻、各频带相对能量大小等时频能量信息，提高信号时频分析精度。

4 结 论

(1)HHT方法中的EEMD分解，能定量评价爆破振动信号的不规则性和复杂程度。根据实测爆破振动信号分解得到的各分量波形及频谱特性确定信号的优势分量为IMF3～IMF6，并利用分形盒维数获得信号优势分量盒维数值区间为1.3≤DB≤1.8，为信号后续分析提供了数据支撑。以广义自相似性因子大小为判断标准，而建立的分形盒维数广义自相似性方法可以准确辨识振动信号主分量，具有很强的可移植性。

(2)EEMD优势分量重组多重分形，定量描述了爆破振动信号的多重分形特征，可以更为精细地评价爆破振动信号的局部标度特征及不同区域的不均匀程度。对于分析爆破振动信号不同层次的特征及概率分布具有非常重要的理论指导意义。

(3)EEMD优势分量重组信号SPWV二次型时频分析，具有良好的局部聚集性，可以有效去除由于模态混叠和交叉项引起的信号能量分布误差，精确描述爆破振动信号的时-频-能分布的细节信息。

(4)文中重点对爆破振动信号单方向(竖向)子信号的时频特征进行了剖析。而水平切向和径向子信号分形能量分布特性有待于进一步研究。同时，采用该组合方法对爆破振动信号三向(径向、竖向、切向)子信号的综合研究，对于深入分析爆破振动波传播机理有积极促进作用，有助于对爆破振动信号的辨识和预测。

[1] ALDAS G G U, ECEVITOGLU B. Waveform analysis in mitigation of blast-induced vibrations[J]. Journal of Applied Geophysics, 2008, 66(1): 25-30.

[2] 蔡宗义,王占江,门朝举,等. 基于Wigner-Ville分布的黄土中爆炸地运动信号传播分析[J]. 岩石力学与工程学报,2010,29(增刊1):3411-3416. CAI Zongyi, WANG Zhanjiang, MEN Chaoju, et al. Propagation analysis of ground motion induced by explosion in loess based on Wigner-Ville distribution [J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(Sup1):3411-3416.

[3] 谢全民,龙源,田作威,等. 爆破振动信号时频特征的三维分形特性研究[J]. 振动与冲击,2010,29(12):118-121. XIE Quanmin, LONG Yuan, TIAN Zuowei, et al. Three-dimensional fractal study on time-frequency characteristics of blast vibration signal[J]. Journal of Vibration and Shock, 2010, 29(12):118-121.

[4] 赵明生,梁开水,罗元方,等. EEMD在爆破振动信号去噪中的应用[J]. 爆破,2011,28(2):17-20. ZHAO Mingsheng, LIANG Kaishui, LUO Yuanfang, et al. Application of EEMD in blasting vibration signal de-noising [J]. Blasting, 2011, 28(2): 17-20.

[5] 凌同华,张胜,陈倩倩,等. 模式自适应小波构造与添加及其在爆破振动信号分析中的应用[J]. 振动与冲击,2014,33(12):53-57. LING Tonghua, ZHANG Sheng, CHEN Qianqian, et al. Pattern adapted wavelet construction and addition and its application to blast vibration signal analysis [J]. Journal of Vibration and Shock, 2014,33(12): 53-57.

[6] 陈仁祥,汤宝平,马婧华. 基于EEMD的振动信号自适应降噪方法[J]. 振动与冲击,2012,31(15):82-86. CHEN Renxiang, TANG Baoping, MA Jinghua. Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal [J]. Journal of Vibration and Shock, 2012, 31(15): 82-86.

[7] 钟明寿,龙源,谢全民,等. 基于分形盒维数和多重分形的爆破地震波信号分析 [J].振动与冲击,2010,29(1):7-11. ZHONG Mingshou, LONG Yuan, XIE Quanmin, et al. Signal analysis for blasting seismic wave based on fractal box-dimension and multi-fractal [J]. Journal of Vibration and Shock, 2010, 29(1): 7-11.

[8] 谢全民,龙源,钟明寿,等.小波与分形组合分析技术在爆破振动信号分析中的应用[J].振动与冲击,2011,30(12): 120-124. XIE Quanmin, LONG Yuan, ZHONG Mingshou, et al. Blasting vibration signal analysis with wavelet and fractal portfolio analysis technique[J]. Journal of Vibration and Shock, 2011, 30(12): 120-124.

[9] 娄建武,龙源,徐全军,等. 爆破地震信号的分形盒维数值分析[J]. 爆炸与冲击,2004, 24(4): 363-369. LOU Jianwu, LONG Yuan, XU Quanjun, et al. A study on the fractal dimension of blasting seismic waves[J]. Explosion and Shock Waves, 2004, 24(4): 363-369.

[10] 马瑞恒,李钊,王伟策,等. 基于小波变换模极大的爆破震动信号奇异谱分析[J]. 爆炸与冲击,2004, 24(6): 529-533. MA Ruiheng, LI Zhao, WANG Weice, et al. The singular spectrum analysis of blasting vibration signal based on WTMM[J]. Explosion and Shock Waves, 2004, 24(6): 529-533.

[11] 王长虹,朱合华. 多重分形与Kriging插值在地层模型生成中的应用[J]. 岩土力学,2011, 32(6): 1864-1868. WANG Changhong, ZHU Hehua. Application of multifractal and Kriging interpolation to reconstruction of stratum[J]. Rock and Soil Mechanics，2011, 32(6): 1864-1868.

[12] 刘树新,刘长武,韩小刚,等. 基于损伤多重分形特征的岩石强度Weibull参数研究[J]. 岩土工程学报,2011,33(11):1786-1791. LIU Shuxin, LIU Changwu, HAN Xiaogang, et al. Weibull distribution parameters of rock strength based on multi-fractal characteristics of rock damage[J]. Chinese Journal of Geotechnical Engineering,2011,33(11):1786-1791.

[13] 赵明生,张建华,易长平. 基于小波分解的爆破振动信号RSPWVD二次型时频分析[J]. 振动与冲击,2011, 30(2): 44-47. ZHAO Mingsheng, ZHANG Jianhua, YI Changping. Blasting vibration signal RSPWVD quadratic time-frequency analysis based on wavelet decomposition[J]. Journal of Vibration and Shock, 2011, 30(2): 44-47.

[14] 池恩安,梁开水,赵明生,等. 小波分解下单段爆破振动信号RSPWVD时频分析[J]. 武汉理工大学学报,2010,32(13):106-109. CHI En’an, LIANG Kaishui, ZHAO Mingsheng, et al. RSPWVD quadratic time-frequency distribution analysis of single deck blasting vibration signal based on wavelet decomposition[J]. Journal of Wuhan University of Technology, 2010,32(13):106-109.

[15] 史秀志,薛剑光,陈寿如. 爆破振动信号双线性变换的二次型时频分析[J]. 振动与冲击,2008,27(12):131-134. SHI Xiuzhi, XUE Jianguang, CHEN Shouru. Quadratic time-frequency distribution analysis of blasting vibration signal based on bilinear transformation[J]. Journal of Vibration and Shock,2008,27(12):131-134.

[16] 郭奇,刘卜瑜,史立波,等. 基于二次EEMD的Wigner-Ville分布旋转机械故障信号分析及试验研究[J]. 振动与冲击,2012,31(13):129-133. GUO Qi, LIU Boyu, SHI Libo, et al. Experimental study and fault signals analysis of machinery based on dual EEMD and Wigner-Ville distribution [J]．Journal of Vibration and Shock,2012,31(13):129-133.

[17] 郝慧艳,李晓峰,刘明杰,等. EEMD和Cohen类联合抑制交叉项的时频特征提取方法[J]. 应用基础与工程科学学报,2012,20(6):1147-1154. HAO Huiyan, LI Xiaofeng, LIU Mingjie, et al. Time-frequency feature extraction method based on EEMD and cohen class to suppress cross terms[J]. Journal of Basic Science and Engineering, 2012, 20(6): 1147-1154.

[18] 刘方,沈长青,何清波,等. 基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法研究[J]. 振动与冲击,2013,32(24):104-109. LIU Fang, SHEN Changqing, HE Qingbo, et al. Wayside acoustic fault diagnosis for locomotive bearings based on Doppler effect correction and EEMD method in time domain [J]. Journal of Vibration and Shock,2013,32(24):104-109.

Analysis of blasting vibration signal based on EEMD fractal andquadratic time-frequency SPWV distribution

YANG Renshu1, FU Xiaoqiang1, ZHANG Shiping2, SU Hong1

(1. School of Mechanics and Civil Engineering，China University of Mining and Technology(Beijing)，Beijing 100083, China;2. College of Mining Technology, Taiyuan University of Technology, Taiyuan 030024, China)

Combining the EEMD (Ensemble Empirical Mode Decomposition) and the fractal box dimension algorithm and considering the statistical self-similar characteristics of blasting vibration signals, an EEMD fractal box dimension generalized self-similarity method was put forward and a generalized self-similarity factor was introduced to identify the principal component of blasting vibration signals. The accuracy of the method was verified by using locomotive vibration signals. A multi-fractal algorithm was used to analyze the original blasting signal and the restructured signal of the dominant component, which describes the multi-fractal characteristics of blasting vibration signals in non scale zone quantitatively. The Cohen quadratic SPWV (Smooth Pseudo Wigner-Ville) time-frequency distribution characteristics of the original signal and the dominant component restructured signal were analysed and compared. The result shows that the method can accurately identify the principal component of vibration signals. The analaysis method integrating the multi-fractal of EEMD dominant component restructured signal and the quadratic SPWV distribution can reveal the local time-frequency characteristics contained in blasting vibration signals and can more effectively improve the modal aliasing, remove the cross-term interference and strengthen the time-frequency aggregation of signals.

blasting vibration; EEMD decomposition; box-dimension fractal; smooth pseudo wigner-ville (SPWV) distribution

国家自然科学基金-面上项目(51274203)

2015-10-15 修改稿收到日期：2015-11-14

杨仁树 男，博士，教授，博士生导师，1963年10月生

TD235.1

A

10.13465/j.cnki.jvs.2016.22.007