星载预应力可展开结构收拢状态的确定、分析与试验

曹长明， 关富玲, 徐 彦， 黄 河

(1.浙江大学 空间结构研究中心，杭州 310058； 2.浙江大学 航空航天学院，杭州 310058)



星载预应力可展开结构收拢状态的确定、分析与试验

曹长明1， 关富玲1, 徐 彦2， 黄 河1

(1.浙江大学 空间结构研究中心，杭州 310058； 2.浙江大学 航空航天学院，杭州 310058)

针对星载预应力可展开结构收拢状态缺乏明确的判定标准，且需满足运载火箭主动飞行段力学环境要求的难点，提出了整星“稳定”收拢状态的确定标准，并对其“稳定”收拢状态下结构的强度、刚度进行有限元分析和相关试验验证，为后续预应力可展开结构收拢状态的研究提供了借鉴。基于星载预应力可展开结构，通过试验研究了捆绳预紧力与收拢状态结构基频及平均熔断时间的关系并确定了捆绳预紧力；利用ANSYS对整星“稳定”收拢状态进行了有限元建模及强度、模态分析；通过振动台试验和锤击法测基频试验对比验证了有限元分析结果的合理性。

预应力可展开机构；收拢状态；力学分析；基频模态；振动台试验；锤击法

随着航天事业的迅速发展，空间结构日趋庞大。由于运载工具有效空间的限制，许多空间结构(如空间平台大型可展天线、太阳帆、伸展臂等)不得不以折叠压缩状送入太空，进入预定轨道后再展开并组装为所设计的几何构形[1]。因此，空间可展开结构的技术研究越来越受到人们的重视，国内外学者对空间可展开结构进行了大量的动力学分析，NASA和Harris公司分别研制了不同的四面体单元天线，对展开原理、结构分析和加工误差影响进行了研究[2-3]。HOKER等[4]在动力学模型建立、微分方程求解、数值分析、运动仿真等方面做了大量工作。肖勇等[5]对大型卫星天线系统进行了固有模态的有限元分析，侯国勇等[6]对桁架式可展开天线进行了模态测试，冯长凯等[7]对3米环肋可展开天线收拢的结构特性进行了分析，关富玲等[8]对双环可展开桁架结构进行了相关动力学分析与试验研究，方永刚等[9]对星载固面可展开天线反射器展开状态进行了模态试验研究。

星载可展开结构具有两种稳定的构形：完全折叠收拢状态和完全展开工作状态。然而，目前国内外的研究都主要集中在后者，对前者的研究相对匮乏，且缺乏明确的判定标准。此外，由于星载可展开结构收拢状态需要满足运载火箭主动飞行段力学环境，是发射成功的关键基础，因此需要对其收拢状态如何确定及相关动力学特性进行深入的研究，是十分迫切必要的。

本文针对用热刀解锁、单根捆绳锁紧的微小卫星载预应力可展开结构的收拢状态，首先通过振动台扫频试验，确立了桁架杆件间添加黏弹性接触件的必要性，进而探究了捆绳预紧力与结构收拢基频及平均熔断时间的关系，提出了星载预应力可展开结构“稳定”收拢状态的概念，明确了对应的捆绳预紧力数值；其次，用ansys对整星“稳定”收拢状态进行了有限元建模及强度、模态分析；最后，通过振动台试验和锤击法测量基频试验的对比，检验了有限元模态、强度分析结果的合理性。

1 整星“稳定”收拢状态的确立

1.1 整星简介

本文研究对象是微小卫星载预应力可展开结构(见图1)。其中微小卫星为边长25 cm的正立方体；可展开结构及附件收拢状态包络尺寸为：26.3 cm×26.3 cm×17.4 cm，展开状态为边长80 cm的正六边形平面桁架。

图1 微小卫星载预应力可展开结构[10]Fig.1 Prestressed deployable structure in micro-satellite

图2 热刀解锁装置Fig.2 Thermal knife unlocking device

收拢状态采用一根Dyneema绳捆扎预紧，解锁采用热刀解锁方式。热刀解锁装置如图2所示。在释放时，通过外接小卫星电源对电热元件通电升温达到Dyneema绳的熔点，即可将紧压在电热元件表面的Dyneema绳熔断，从而可展开结构被释放并且在自身扭簧弹性能的作用下逐渐展开。Dyneema绳断开后，在自身预紧力及杆件向外的推动力作用下，会从可展开结构表面脱落，不影响可展开结构的展开。

1.2 捆绳预紧力值的确定

为了避免捆绳产生过大蠕变且保证足够预紧力使捆绳与热刀解锁装置的电热元件紧密接触，需要确定捆绳的预紧力。除了上述因素以外，影响捆绳预紧力的参数主要是结构基频和平均熔断时间。

采用不同的捆绳预紧力锁紧结构分别进行振动台扫频试验(见图3)和热刀解锁展开试验(室温25℃)(见图4)。为避免锁紧状态下的可展开结构部件之间的碰撞和减少结构的共振效应，在构造上设置如图5所示的黏弹性接触件以保证结构整体刚度。

图3 振动台扫频试验Fig.3 Frequency scanning vibration test

图4 热刀解锁试验(25℃)Fig.4 Thermal knife unlocking test

图5 黏弹性接触件实体图Fig.5 Viscoelastic contact

试验数据如表1所示，各组扫频曲线(见图6)，同时可以得到捆绳预紧力与结构基频(曲线的第一个峰值，实际为第四阶，见下文)和平均熔断时间的关系曲线(见图7、图8)。

表1 结构基频及平均熔断时间测试结果Tab.1 Test results of structural natural frequency and average operation time

图6 各组扫频试验曲线对比图Fig.6 Comparison chart of each frequency test curve

图7 捆绳预紧力与结构基频的关系曲线Fig.7 Relationship curve of cord’s pre-stress and structural natural frequency

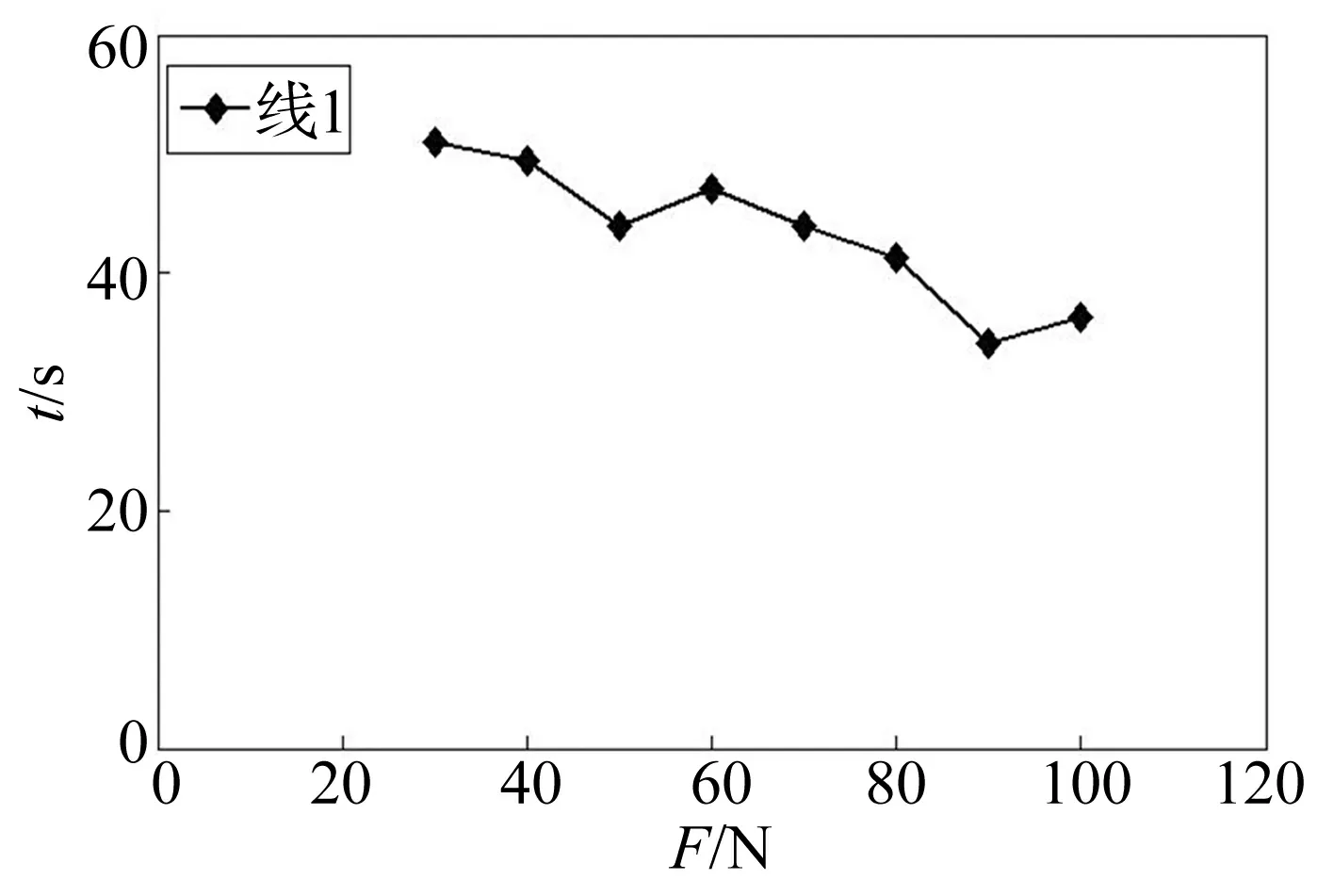
图8 捆绳预紧力与平均熔断时间的关系曲线Fig.8 Relationship curve of cord’s pre-stress and average operation time

从图7可知，收拢锁紧状态下，可展开结构的基频与捆绳预紧力密切相关，可分为三种状态：①捆绳预紧力小于50 N时，可展开结构杆件之间还未完全接触，即黏弹性接触件还未发挥有效作用；②捆绳预紧力介于50 N～80 N之间时，即杆件之间处于紧密接触状态，即黏弹性接触件开始发挥有效作用；③捆绳的预紧力大于80 N时，结构基频增加不明显，即杆件之间的黏弹性材料发挥有效作用，结构形成近似刚性整体，处于“稳定“收拢状态。据图7可得，捆绳平均熔断时间与捆绳预紧力呈负相关的关系，即捆绳预紧力的增加有助于捆绳更快的熔断。

根据上述试验结果，综合考虑运载发射阶段锁紧结构的基频要求、捆绳蠕变、薄壁碳纤维杆件承载力等因素，确定捆绳预紧力值为100 N(控制精度为±3 N)。

1.3 确定整星“稳定”收拢状态

对于这种在收拢状态下是离散桁架结构、捆绳(或其它)锁紧状态下杆件间仍具有较大间隙的预应力可展开结构，提出了确定整星“稳定收拢”状态的标准。

即预应力可展开结构在捆绳(或其它)锁紧状态下，随着预紧力的增大，整星收拢状态的基频不断提高，当收拢基频增大到一定程度后开始收敛，趋于一个稳定数值，此时我们即判定整星进入“稳定”收拢状态。由图7可判断，当捆绳预紧力为80 N时，整星即开始进入“稳定”收拢状态。

2 整星稳定收拢状态力学分析

在整星稳定收拢状态确定后，需要对其稳定收拢情况下结构的强度、刚度进行分析，以分析是否满足运载火箭主动飞行段力学环境的需求。

可展开结构在稳定收拢状态时，其外围用一根迪尼玛绳在中间处捆紧(预紧力为100 N)。可展开结构在完全展开状态时，卫星位于其中心。如图1(c)所示。

2.1 有限元建模

采用ANSYS软件进行有限元分析。整个可展开结构由节点、杆件、扭簧、销轴、接触件、捆绳以及其余固定配件组成。本模型中只对前6种进行单元建模，其余用附加质量方式体现在模型中。节点分为中心花盘节点，6个六向节点，6个三向节点，6个四向节点，以下统称为花盘节点，其单元均选取壳单元Shell 63，杆件间的双向节点，碳纤维杆件以及销轴均选用梁单元Beam188，扭簧采用真实的刚度，采用线性弹簧单元Combin14单元分析，扭转角为125°(展开状态为35°)；对于捆绳，采用LINK10单元模拟，仅受拉；对于杆件之间的黏弹性接触件，采用LINK10单元模拟，仅受压。

本展开结构包含非线性弹簧，无法进行严格意义上的模态分析。但可展开结构在收拢状态下由于捆绳的张力作用和黏弹性阻尼材料的接触作用，使得各杆件间紧密连接，再加上杆件与节点侧板的接触，因此，可以将收拢状态的扭簧作用点处等效为刚接，即整星处于“稳定”收拢状态。

对于星体，等效成为6个Shell 63单元，厚度为实际厚度，星体内部的器件通过改变星体的材料密度来添加；分离结构等效为四根在星体四角的梁单元。约束条件为：将分离结构的底端刚接，即四根梁的底部节点约束住所有的自由度。建好的有限元模型如图9所示。

图9 收拢状态有限元模型Fig.9 Folded state finite element model

2.2 强度分析

随机振动环境是航天器结构强度设计重点考虑的

因素之一。目前，航天器所经历的随机振动通常用加速度谱来描述，设计载荷最普遍采用的原则就是加速度峰值响应等效，即设计载荷所产生的加速度响应等于随机振动中的加速度响应峰值。在外载荷激励下，加速度响应等效的公式可表达为:

(1)

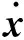
本例取等效加速度峰值为x向、y向、z向30 g(依据欧洲航天局和我国航天系统内部的初始分析等效标准)。ansys分析结果如图10所示。

由上述分析结果可知，在横向(+x，+y)30 g下，整星的最大位移为5 mm，最大应力为62 MPa，应力最大处发生在中心花盘节点与销轴连接处(见图10(a),图10(b));竖向(+z)30 g下，整星最大位移为2.6 mm,最大应力发生在小卫星与展开机构相连的“脖子”处，大小为49.6 Mpa(见图10(c))，其余地方应力较小。其中，铝合金型号为2A12，屈服强度265 Mpa，安全系数为:

n=[σ]/σ=265/62=4.27

(2)

即说明在满足刚度设计的前提下，强度设计安全余度也足够。

图10 整星各向30 g等效应力云图Fig.10 Von mises stress of overall satellite (30 g)

2.3 模态分析

结构的固有频率与振型(模态)反映结构的刚度特性,频率的高低、振型分布均匀性、疏密情况是结构整体刚度的重要表现。通过对模态分析所得的各阶频率和相应振型进行分析，可以判别出结构的薄弱环节，为改进结构性能提供第一手资料，并可以有效地避免结构与周围空间发生共振。

本文对所建立的整星模型进行模态分析，所得到的前6阶固有频率和振型见表2。

表2 前六阶固有基频及振型Tab.2 Fundamental frequency and modal of folded state

3 整星振动台试验

整星振动台试验包括：整星基频扫描试验、整星低频振动试验、整星随机振动试验三部分。单向加速度传感器的布置方式如图3所示(测量z方向加速度)。试验结果(图12、图13、图14)所示。

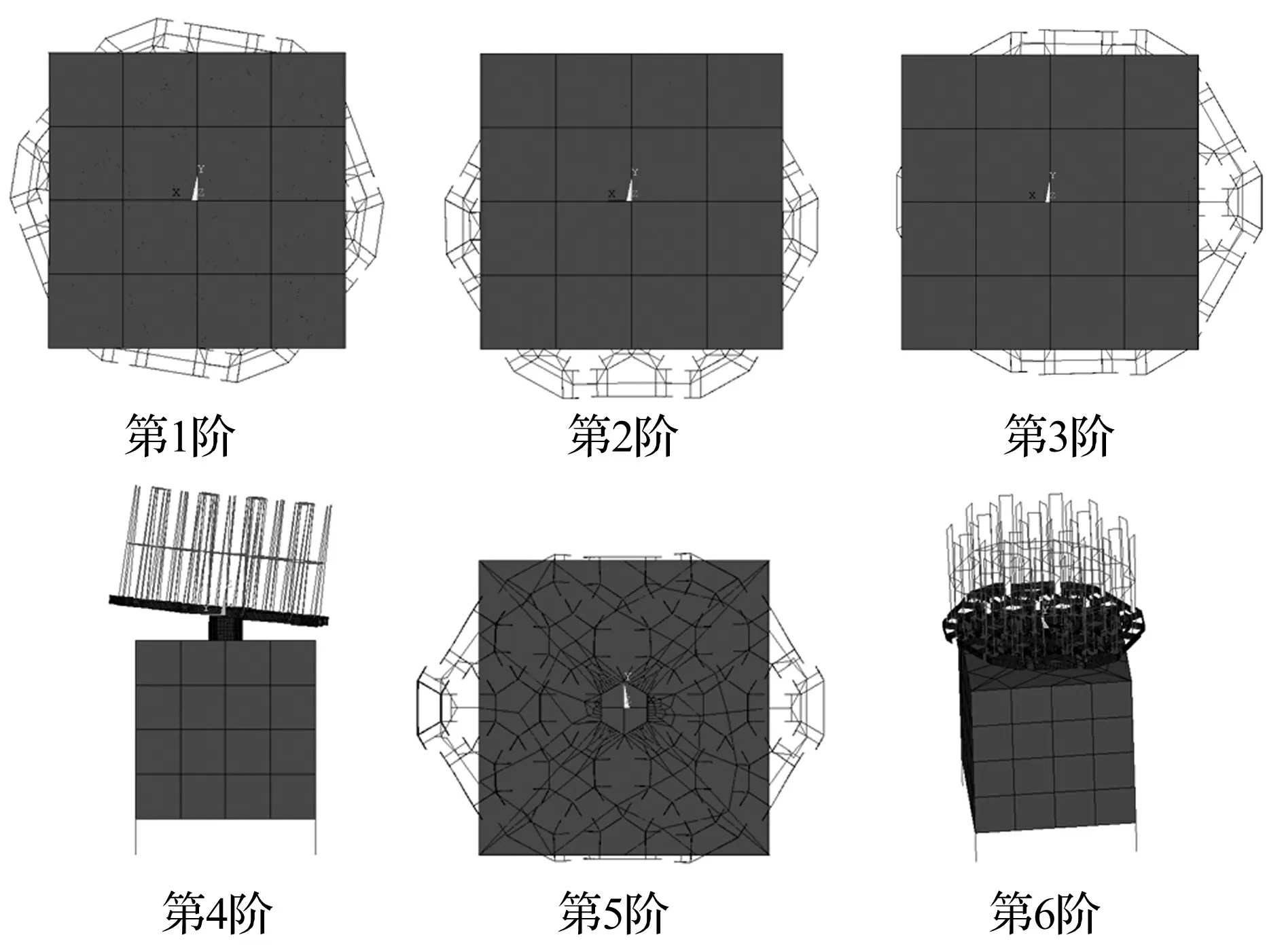
图11 整星收拢状态前六阶振型图Fig.11 First six modes of vibration of folded state modal

图12 扫频试验结果(深色线为传感器输出信号)Fig.12 Results of vibration frequency sweep test

图14 整星随机振动试验输出结果 Fig.14 Results of random vibration test

试验结果如下:

(1)整星基频扫描试验时，由于其振动台激励为单向(x向)激励，且加速度传感器为单向传感器，其安装位置如图3，只能测量z向加速度，且由上节有限元分析结果可知，其前三阶振型(展开结构绕z轴转动、沿y轴平动、沿x轴平动)无z向的加速度，第四阶振型(展开结构左右上下摆动)开始出现z向加速度，因此判断扫频试验结果显示的第一个峰值为有限元分析的第四阶基频，试验结果约为118 Hz左右，有限元分析结果为104.9 Hz。此外，多次用高帧数(120 P)摄像机对振动台扫频试验录像的分析结果也表明，其扫频曲线的最高峰值处，可展开结构振型明显为左右上下摆动。由此，可以判定：整星的第四阶基频为118 Hz左右，振型为可展开结构左右上下摆动，试验结果与有限元分析结果基本吻合。进而掌握收拢状态结构的刚度情况。

(2)通过低频振动试验结果(见图13)可知，其共振最高点在85 Hz左右，通过随机振动实验结果(见图14)可知在我们关注的区间300 Hz内没有明显共振点，响应较低，且振动后检查可展开结构上的所有构件在振动后无破坏，也没有发生塑性变形，证明该结构设计安全可靠。

4 锤击法测量整星收拢状态基频

采用锤击法测量整星收拢状态的基频，如图15所示。

图15 锤击法测基频Fig.15 Hammering method to measure fundamental frequency

试验测量结果如下：

试验结论：①由频响函数图可知，第一个尖峰值(1阶基频)为25.4 Hz，第二个51.1.第三个尖峰为81.6 Hz，第四个为101.6 Hz。由图18可知响应和激励的相干函数较好，峰指出基本接近1，说明锤击法试验数据是可靠的。②由图19可知，锤击法测基频的试验结果与有限元分析结果基本吻合。证明有限元分析结果合理可信。

图16 时域函数Fig.16 Time domain function

图17 频响函数Fig.17 Frequency response function

图18 相干函数Fig.18 Coherence function

图19 锤击法与有限元分析结果对比Fig.19 Comparison between hammering method and finite element analysis

4 结 论

本文针对收拢状态下是离散桁架结构、捆绳(或其它)预紧状态下杆件间仍具有较大间隙的预应力可展开结构，提出了整星“稳定”收拢状态的确定标准， 明确了对应的捆绳预紧力数值；对整星收拢状态做了有限元建模和强度、模态分析，结果表明均符合设计要求；通过振动台试验、锤击法测量基频试验同有限元分析结果的对比，检验了有限元强度、模态分析结果的合理可信性。

[1] 赵孟良，吴开成，关富玲. 空间可展桁架结构的动力学分析[J].浙江大学学报(工学版)，2005,39(11):1669-1674. ZHAO Mengliang, WU Kaicheng, GUAN Fuling. Dynamic analysis of deployabke space truss structure[J]. Journal of Zhejiang University(Engineering Science),2005,39(11):1669-1674.

[2] MIURA K, FURUYA H. Variable geometry truss and space crane arm[J]. Acta Astronautica,1985,12(7):599-607.

[3] MIURA K, FURUYA H. Adaptive structure concept for future space applications[J]. AIAA Journal,1988,26(8):995-1002.

[4] HOKER W W, MARGULIES G. The dynamics attitude equations for an n-body satellite[J]. Journal of Astronautial Science,1965,12(4):123-128.

[5] 肖勇，王三民，陈国定. 大型卫星天线系统固有模态的有限元分析[J].机械设计与制造，2006, 7(7)：1-2. XIAO Yong, WANG Sanmin, CHEN Guoding. The modal analysis for satellite-large space antenna system with finite elemernt method(FEM)[J].Machinary Desgn& Manufacture,2006,7(7):1-2.

[6] 侯国勇. 桁架式展开结构设计、分析及试验[D]. 杭州:浙江大学,2008.

[7] 冯长凯.星载可展开机构的动力学仿真分析[D].西安:西安电子科技大学,2008.

[8] 关富玲，戴璐. 双环可展桁架结构动力学分析与试验研究[J].浙江大学学报(工学版)，2012,9(9):1605-1610. GUAN Fuling, DAI Lu. Dynamic analysis and test research of doublering,deployable truss structure[J]. Journal of Zhejiang University(Engineering Science),2012,9(9):1605-1610.

[9] 方永刚，于新战，王磊,等. 星载固面可展开天线反射器展开状态模态试验研究[J].空间电子技术,2014,11(2):32-35. FANG Yonggang, YU Xinzhan, WANG Lei. Modal test research of the deployable rigid reflector for satellite antenna[J]. Space Electronic Technology,2014,11(2):32-35.

[10] 朱术华，关富玲. 小型星载可展开结构的平面度测量[J]. 低温建筑技术，2015，37(6)：37-39. ZHU Shuhua, GUAN Fuling. Flatness precision measurement of small spaceborne deployable planar mechanism[J]. Low Temperature Construction Technology,2015,37(6):37-39.

[11] 张玉梅，韩增尧，邹元杰. 随机振动环境下航天器结构强度设计方法综述[J].力学进展,2012,42(4): 464-471. ZHANG Yumei, HAN Zengyao, ZOU Yuanjie. An overview of structural strength design methods for spacecrafts in random vibration envir onment[J]. Advances in Mechanics, 2012,42(4): 464-471.

Determination, analysis and test on the prestressed folded state of spaceborne deployable structures

CAO Changming1, GUAN Fuling1, XU Yan2, HUANG He1

(1. Space Structure Research Center, Zhejiang University, Hangzhou 310058, China;2. School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310058, China)

Due to the lack of specific criteria for the prestressed folded state of spaceborne deployable structures, and the difficulty in meeting the mechanical environmental requirements in the phase of rocket active flight, a kind of criteria was put forward to determine the entire star “stable” folded state. Finite element analyses and related experiments were carried out for understanding the structural strength and stiffness at the “stable” folded state to give a reference to the following study. Based on this spaceborne prestressed developable structure, tests were conducted to study the relationship of the cord pretension wiht the structural natural frequency in folded locking state and the average locking operation time. Then the pretension was determined. The intensity and modes of the entire structure in “stable” state were analysed by ANSYS software. The rationality of the finite element analysis results was verified by comparing the shaking-table test results with the fundamental frequency measurements by using the hammering method.

prestressed deployable structure; folded state; mechanical analysis; fundamental mode; shaking-table test

国家863基金资助项目(128205-E31403)；国家自然科学基金(11402229)；浙江省自然科学基金(LQ14A020003)

2015-08-07 修改稿收到日期：2015-11-11

曹长明 男，硕士，1988年生

关富玲 女，博士，教授，1945年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2016.22.020