新型纵扭压电电机接触模型研究

李 冲， 鹿存跃， 马艺馨， 黄卫清

(1. 上海交通大学 仪器科学与工程系, 上海 200240； 2. 南京航空航天大学 精密驱动所,南京 210000)



新型纵扭压电电机接触模型研究

李 冲1， 鹿存跃1， 马艺馨1， 黄卫清2

(1. 上海交通大学 仪器科学与工程系, 上海 200240； 2. 南京航空航天大学 精密驱动所,南京 210000)

提出一种新型贴片式纵扭压电电机，包含定子，转子和预压力系统等。电机定子经过特殊的开槽处理形成多振子结构，振子由金属基体和粘贴在其外表面的压电陶瓷构成，益于简化电机结构。通过合理的参数调整，使定子的一阶纵振模态和二阶扭转模态频率尽可能相同，并且振子均工作在共振状态，提高了电机效率。为评估设计电机的整体性能，建立了定子和转子的有限元接触模型，并对电机的接触特性进行分析研究。通过接触静态和瞬态求解，得到空载情况下接触区的压力分布、接触状态及滑动距离等参数，同时得到电机的转速变化曲线和输出性能等。分析结果表明该纵扭电机为多面接触，接触压力不存在局部高度集中的情况，且接触区域存在滑动。最后，根据设计的电机参数，加工原理样机，对理论分析进行实验验证。

压电电机；有限元；接触模型；多面接触

压电电机利用压电材料的逆压电效应将输入的电能转化为定子驱动质点的振动能，再通过定子和转子之间的摩擦作用直接驱动转子或滑块运动[1-3]。其中，纵扭型压电电机采用纵向和扭转的复合振动模态，在原理上能获得比行波型和摇头型电机等更大的扭矩。常规纵扭型电机的扭振片采用8个扇形压电片组装而成[4]，它利用陶瓷材料的d15逆压电效应激励出扭转振动。由于扭振片的极化方向与激励电场方向相垂直，需两次制作电极，加工工艺复杂，质量难以控制，成本较高，因而较难实现。同时该电机需要两个振子才能在驱动面上形成椭圆振动，使得电机结构复杂，设计和加工困难。为简化电机结构，出现了只采用纵振片激励的开孔或开槽的模态转换型纵扭电机[5]，但该电机效率不高，只能单向运转。本文提出一种构造贴片式纵扭电机的方法，易于简化电机结构；电机定子经过特殊的开槽处理形成多个振子；为提高电机效率，改变开槽尺寸使定子的一阶纵振模态和二阶扭转模态的频率尽可能相同，并且振子均工作在共振状态，质点的输出位移较大。压电陶瓷沿厚度方向极化，与施加的电场方向平行，利用陶瓷的d31逆压电效应激励出定子驱动质点的纵扭复合振动。该方法简化了电机结构，利于其微型化。

纵扭型压电电机的能量损耗主要来自定子和转子接触面的摩擦损失，且所有的输出能量均通过定子和转子间的摩擦耦合来传递，而摩擦耦合作用会直接影响电机的输出性能，因此对定子和转子间摩擦模型的研究对该类电机的设计具有重要意义。到目前为止，许多学者已经对行波型压电电机的接触模型进行了具体的研究[6-8]，其中MAENO等用有限元法研究了相机镜头上所用的中空行波电机[4-16]，但是对纵扭电机的研究较少。相对于传统的纵扭电机，本文所设计的电机在工作原理、定子的振动特性、定子和转子的接触区及摩擦界面的驱动特性等都不同。为了评估设计电机的整体性能，本文对其接触特性进行分析研究，并且建立定子和转子的有限元接触模型。通过对接触模型静态和瞬态过程的求解，分析设计电机的整体运行情况。最后，根据设计的电机参数，加工原理样机，对理论分析进行实验验证。

1 电机结构

该电机主要由定子、转子和预压力系统等构成，预压力系统包括碟簧、螺母和轴等，电机的具体结构如图1所示。电机定子包含金属基体和粘贴在其外表面的压电陶瓷。沿定子基体的圆周方向均匀开槽形成N个相同的振子(N≥3)，同时金属基体的外表面粘贴N组压电陶瓷片，每组包含2片，分别用以连接相位差为90°的正弦激励信号。经综合考虑，选择的振子数为5，定子的结构参数如图2所示。

图1 电机结构Fig.1 The motor structure

定子各参数值如表1所示，表中长度单位为mm。其中，R1、R2和R3代表圆筒形定子的内、外半径，而R2和R3的差为压电陶瓷体的厚度(0.5 mm)；d1为在定子中部基线处对称的开槽弧度(基线所在的角度为n×2π/5，n取1～5之间的整数)；d2是为实现频率一致性，在d1基础上对称增加到的开槽弧度，从而在定子两端形成细径，同时起到放大输出位移的作用；H为整个定子的高度；h2是两端细径的高度；h1-h2是定子两驱动端的高度；φ为每个振子上粘贴的一组陶瓷的弧度，因而每片陶瓷的弧度为φ/2。

表1 定子参数值Tab.1 The parameter values of the stator

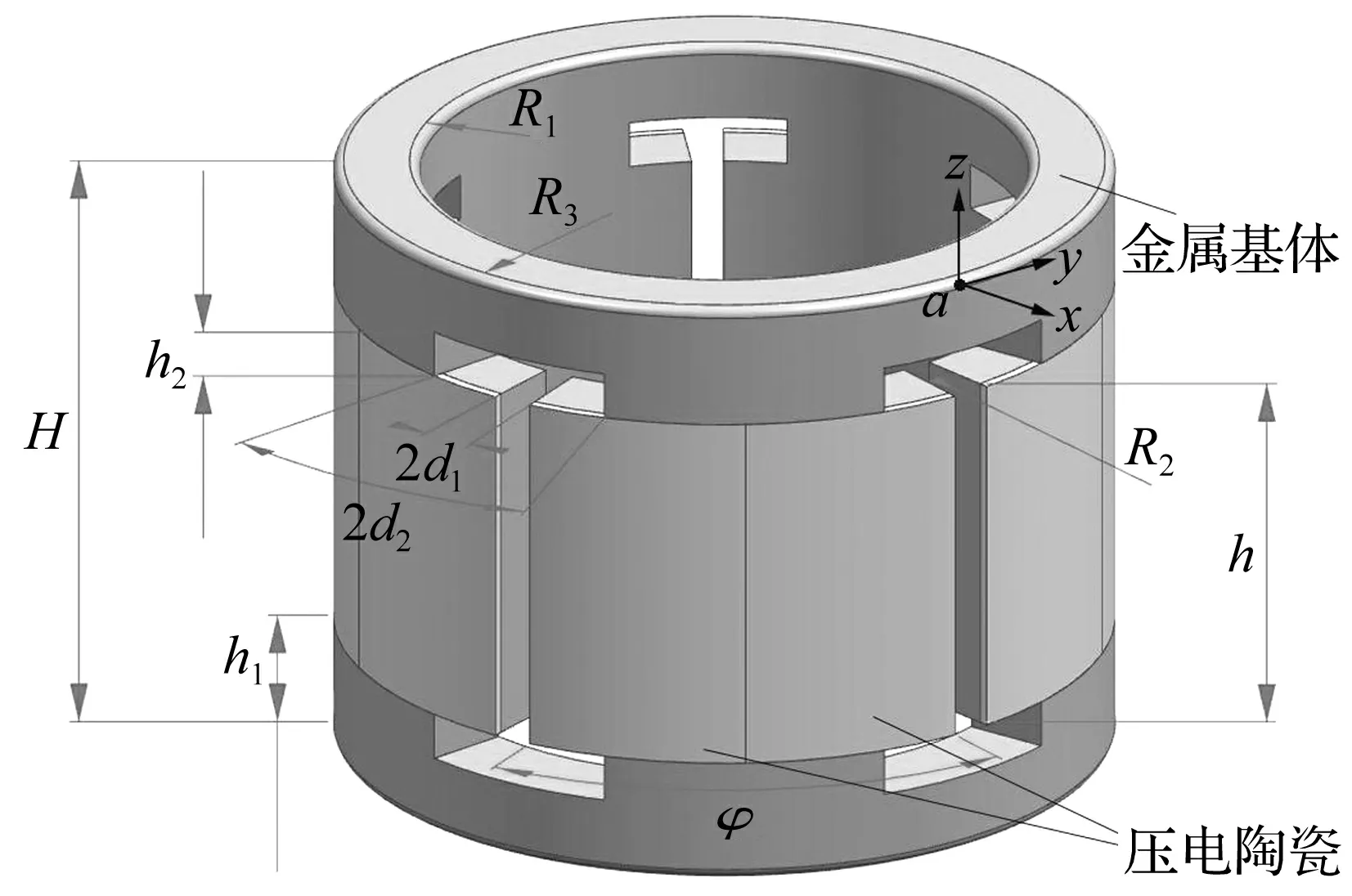
图2 定子结构参数Fig.2 The structural parameters of the stator

电机使用定子的一阶纵振模态和二阶扭转模态的复合模态为工作模态，如图3所示。当图1中两相输入电压的方向相同时，每组压电片同时伸长或缩短，激励出振子的纵振模态；当两相输入电压的方向相反时，每组压电片，一边伸长，一边缩短，形成振子的弯振模态，进而转化为圆环形定子的扭转模态。调整表1中的参数值可以使得定子的一阶纵振模态和二阶扭转模态的频率接近一致；再通过粘贴在定子基体上的压电陶瓷施加相位差为90°的两正弦激励信号，可同时激励出定子工作所需的两个振动模态；激励信号的频率等于定子的共振频率时，各振子均工作在共振状态且同步工作。在有一定相位差的纵振和扭转复合共振模态下，定子上、下驱动表面上质点的运动轨迹为椭圆，其中，定子驱动端面的周向振动驱动转子旋转。

经模态分析可得，定子的一阶纵向和二阶扭转模态频率依次是46.852 kHz和46.818 kHz，二者之差为34 Hz。

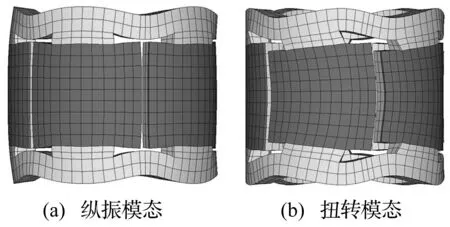
图3 使用的定子模态Fig.3 The used modes of the stator

2 质点振动方程

首先，从理论上分析设计的电机定子驱动端面上质点的变化趋势与定子和转子之间的摩擦驱动原理,与行波型电机由行波方程导出驱动面质点的位移表达式不同，纵扭型压电电机的质点位移由椭圆轨迹得到。假设定子驱动端质点(见图2中a点)的纵向和切向位移表达式如下：

uy=Asinωt

(1)

uz=Bsin(ωt+φ)

(2)

式中，uy为切向位移，uz为纵向位移，A和B为相应的振幅值，φ为二者之间的相位差。当纵向位移达到某一值时，定子和转子相接触，二者之间存在一定的压力，此时，定子驱动面质点的扭转振动驱动转子旋转。在接触区域内，可能存在着复杂的接触模式，定子和转子之间可能黏结，也可能滑动。

由式(1)和式(2)可得，定子驱动端面质点的切向和纵向速度为:

vy=ωAcosωt

(3)

vz=ωBcos(ωt+φ)

(4)

假设稳态时，转子速度为v0。由式(3)可知，定子驱动端质点的切向运动速度是正弦变化的，而转子的运动是靠定子驱动端面质点的扭转运动来传递的，所以电机运行时，定子驱动端面上质点的切向最大速度一定大于转子的平均速度v0。因此vy一定会出现与v0相等的点，简称等速点。

假定法向作用力T，摩擦力为F。根据库仑定律，当F=μT时，该点为滑动点；当定子表面质点的切向速度vy小于v0时，摩擦力为阻力；否则为推力。当F<μT时，该点为黏滞点。其中μ为摩擦因数。当电机稳态运行时，定子和转子之间持续的断续接触，其中在接触阶段，定子对转子有一定的冲击力。当定子质点的纵扭转位移改变时，冲击力随之变化。

3 定子和转子接触模型

为了得到设计的电机定子驱动端面质点的具体振动情况，定子和转子之间的接触状态以及电机的输出特性等，本文采用有限元分析软件ANSYS建立定子和转子间的接触模型，如图4所示。为考虑激励信号的电压、频率和相位差等因素对结果的影响，该模型采用三维耦合场体单元SOLID5对压电陶瓷进行网格划分，其它结构采用SOLID45单元进行网格划分。由于设计的电机是面接触模式，因此接触模型中使用目标单元TARGE170与接触单元CONTA174定义定、转子之间的面接触对。由于定子的弹性模量大于转子的弹性模量，因此，定义定子上表面为接触对的目标面，定义与定子相接触的转子下表面为接触面，并对接触对分配实常数号，定子和转子之间的摩擦因数取0.3，摩擦材料厚0.3 mm。

图4 有限元模型Fig.4 The finite element model

为使得建立的有限元模型更加符合电机的实际运行情况，模型还需符合以下条件：瞬态接触分析时，在每组压电陶瓷体上施加相位差为90°的两相激励信号。激励电压的峰值和频率分别设为100 V和46.8 kHz；为简化仿真模型，省去轴等预压力机构，直接在转子上表面施加轴向预压力；在定子中性面的内侧节点施加径向位移约束，以阻止定子平面的平移运动；在两转子上表面节点施加径向位移约束，使转子只做周向旋转运动而不做平面平移运动；同时转子上表面的节点耦合轴向自由度，即该节点轴向位移一致；负载扭矩可按照等效切向力的方式施加在转子上表面的内侧节点上。仿真模型中使用的材料的具体参数如表2所示。

4 仿真结果分析

分析得到的结果如下：当在转子上表面施加一定的预压力，对接触模型进行瞬态接触分析时，定子和转子之间的接触面随时间的变化逐渐趋于稳定。图5为定子驱动端质点的轴向位移稳定时定子和转子之间的平均接触状态图。分析中，激励信号的周期设为400，总时间约8.6 ms，每周期分30个点，时间步长约0.7 μs。图5中，Ⅰ区为Near Contact，表明定子和转子刚接触；Ⅱ区代表Sliding，表明二者之间接触良好并且具有一定的切向滑动，因此该区可用于驱动转子旋转；Ⅰ区和Ⅱ区交错分布。下文所指的接触面即定、转子之间的驱动面，均指Ⅱ区。仿真结果表明设计电机的接触状态介于行波型电机(若干点接触)和传统的纵扭型电机(整个面接触)之间，是多面接触。该结果主要与定子基体处的开槽有关，开槽改变了定子的局部刚度，使得定子和转子之间的接触状态发生改变，从而使未开槽处的接触变差，改变电机的面接触模式。此外，在将环形振子的弯振模态转换为整个定子的扭转模态(见图3(b))时，定子两驱动端处会产生局部变形，从而引起定子驱动端处质点的纵振幅度发生不同程度的变化，进而也会改变电机的接触状态。

表2 材料参数Tab.2 Parameters of the materials

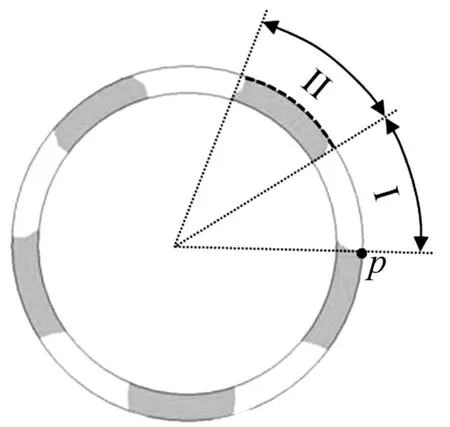
图5 定子和转子之间的平均接触状态Fig.5 The average contact state between the stator and rotor

计算得到的平均接触面积为0.12×10-3m2，整个目标面为0.23×10-3m2，接触面积的百分比约52%。定子细径处的总开槽弧度5×2×d2约为整个圆周的一半，与仿真得到的接触面积百分比相符。单位面积的压力和摩擦力分别是0.37×107N和0.11×107N，由于每个接触单元的质点所受压力不同且随时间改变，上述结果是平均值。用平均压力值乘以接触面积得到总压力，得到的总压力和摩擦力为8.27 N和2.48 N，该方法会造成计算的接触力与实际值有一定的偏差。

瞬态分析可以得到接触区内质点受到的压力随时间的变化曲线。图6是定子驱动端的质点位移稳定后，接触点(见图5中p点)在一个周期内压力随时间的变化曲线，该曲线近似等同于定子和转子之间的接触状态。当压力为零时，定子和转子相互分离；压力越大，接触状态越好。由式(4)可知，定子振动稳定时，纵向位移正弦变化。当位移达到一定值时，定子和转子之间接触，二者之间有压力，因此，接触质点所受的压力随时间的变化曲线是正弦曲线的一部分，与结果相符。图6中接触时间约为整个周期的60%。

图6 压力随时间的变化曲线Fig.6 The curves of pressure with time

图7为4.255 ms时接触路径上(见图5中虚线所示)压力的变化曲线，由于该电机是多面接触，因此定义的路径只包含其中一个接触面。仿真结果表明设计的电机接触良好，接触压力不存在局部高度集中的情况，符合该电机的多面接触特性。

图7 接触区不同位置所受的压力Fig.7 The pressure of different position at the contact region

取定子接触区外径处的一点(见图5中p点)，驱动点的滑动距离随时间的变化曲线如图8所示。前200个激励周期中，输入电压幅值设为100 V，200个周期后，激励电压清零。由图8可得，激励时间内质点的滑动距离与时间成线性关系，当激励信号关闭，滑动距离不变。

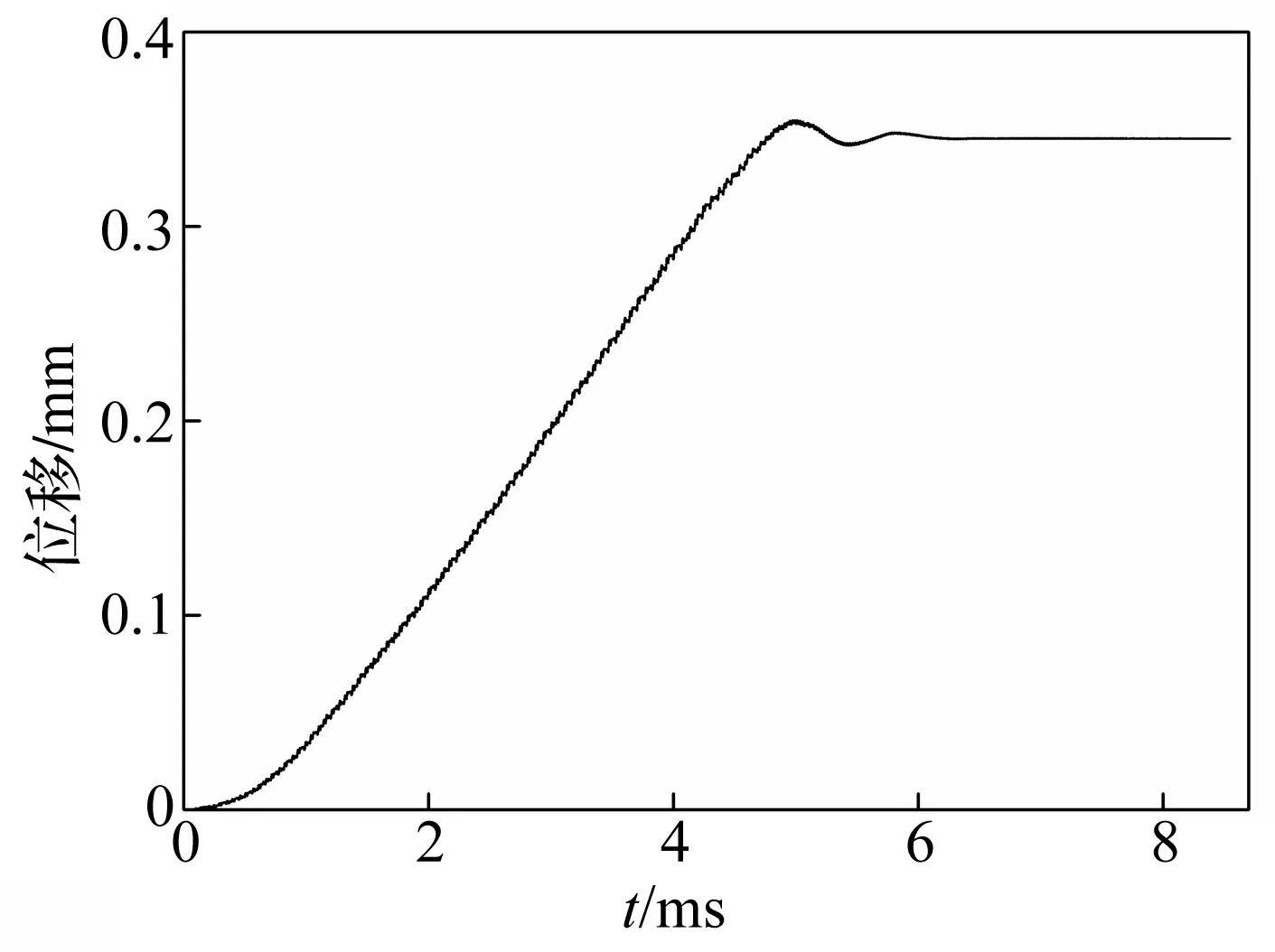
图8 定子质点的滑动距离Fig.8 The sliding distance of a stator particle

图9为电机空载时，定子和转子接触表面，质点(见图5中p点)的切向速度在一个周期内的变化曲线。空载时，转子的速度在一定范围内恒定；定子速度呈正弦变化趋势，频率等于激励信号的频率，与理论分析相符。

图9 定子和转子的切向速度Fig.9 The tangential velocities of the stator and rotor

5 结 论

本文提出了一种新的纵扭型电机，其设计原理不同于传统的纵扭电机。为具体分析设计电机的振动和摩擦接触特性等，使用有限元法对其接触模型进行了研究，得到定子和转子间的接触状态，接触压力随时间和位置的变化等。

为验证仿真结果，按照表1的参数值，加工原理样机。其中，金属基体为黄铜材料，压电材料为PZT-8，摩擦材料采用聚四氟乙烯，转子使用硬铝，通过弹簧在定子表面施加预压力。采用激光多普勒测振仪测得定子的二阶扭转频率和一阶纵向频率分别是43.828 kHz和44.420 kHz。由于定子的实际开槽误差和压电陶瓷的尺寸偏差等问题，造成计算出的共振频率与实际的测试结果有一定的偏差。当激励电压峰值为100 V，频率43.9 kHz时，测得定子驱动端面质点的纵向和扭转位移依次约1 μm和1.3 μm，验证了所设计的电机具有良好的振动特性。

图10为俯视测得的定子驱动端面质点的纵向振动曲线，A处代表定子和转子接触区的一部分，实验结果验证了该电机的多面接触模式，接触面个数由定子径向开槽形成的振子数所决定，与仿真结果相符。

图10 定子纵振曲线Fig.10 The longitudinal vibration curve of the stator

接触瞬态分析得到的转速变化曲线如图11所示。同时，参考文献[17]中的测试方法，对加工的样机进行实验研究。图11中包含了实际测得的电机转速曲线，图中的离散点是经过实验获得的数据点，实线是拟合后的曲线。测量条件为：激励电压的峰值为100 V，频率43.9 kHz。由图11可知,仿真得到转速稳定值约51 r/min，测得的转速稳定值约45 r/min，该偏差是由于未考虑摩擦损耗和电机升温对定子共振频率的影响及加工偏差等因素的影响，使得转子的实际转速小于仿真值。此外，由图11推断，转速的过渡过程近似为一阶滞后环节，其变化趋势与传统纵扭电机相似，实际测得的转速变化曲线与仿真结果趋势相符。仿真得到的转速启动时间约3 ms，但电机在实际工作中，由于受预压力、温升、定子驱动表面的平滑程度等因素的影响，会使得电机的实际启动时间大于该值，实际测得的启动时间约6 ms。

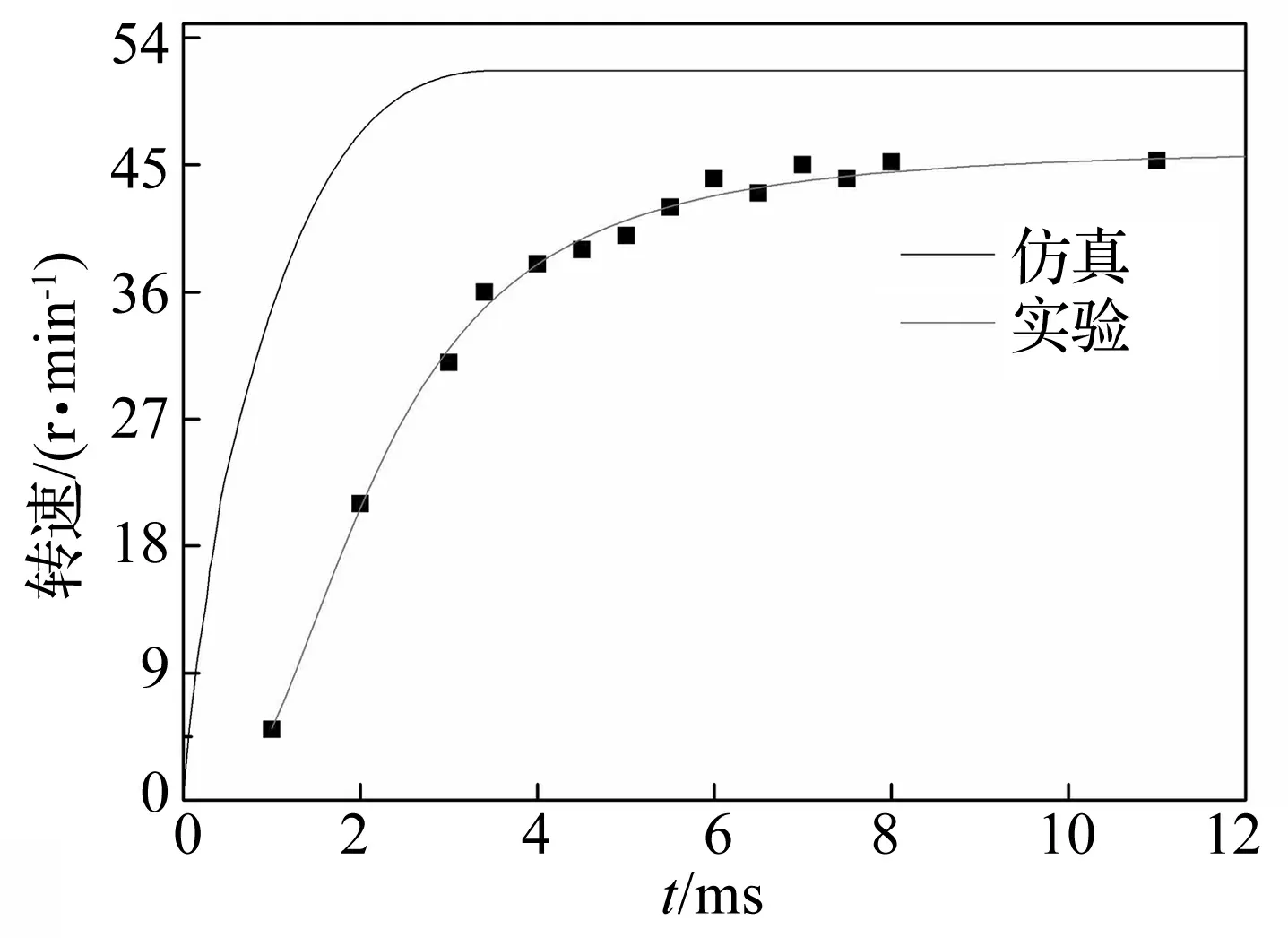
图11 转速随时间的变化曲线Fig.11 The speed curves change with time

电机的输出扭矩与转速关系如图12所示，二者近似成线性关系。测得电机的空载转速约45 r/min，堵转力矩0.3 N·m，小于仿真值0.4 N·m。实验结果表明设计的电机性能良好，同时验证理论分析的正确性，表明该接触分析可用于评估电机的整体输出性能。

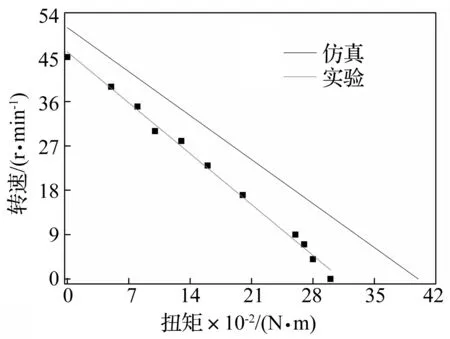
图12 电机输出特性曲线Fig.12 The output characteristic curves of the motor

综上所述，本文提出了一种新型贴片式纵扭压电电机，包含定子，转子和预压力系统等。电机定子经过特殊的开槽处理形成多振子结构，振子由金属基体和粘贴在其外表面的压电陶瓷构成，益于简化电机结构。通过合理的参数设计，使定子的一阶纵振模态和二阶扭转模态频率尽可能相同。同时，振子均工作在共振状态，提高了电机效率。为评估设计电机的整体性能，建立了定子和转子的有限元接触模型，对电机的接触特性进行研究。结果表明该电机为多面接触模式，接触压力不存在局部高度集中的情况，且定、转子接触面内的质点所承受的压力不同。同时金属基体的开槽个数决定了接触面数和电机的输出功率等特性，电机的实际输出性能应介于行波型电机和传统纵扭电机之间。最后，根据设计的电机参数，加工原理样机，进行实验验证。电机性能良好，利于将该类电机推向实用化。

[1] 甘云华，金龙，王心坚，等．超声波电机自激振荡驱动电路的变频控制特性[J]．中国电机工程学报，2008, 28(9): 93-97. GAN Yunhua, JIN Long, WANG Xinjian, et al. Characteristic of variable frequency control of self-oscillating driving circuit for ultrasonic motor [J]. Proceedings of the CSEE, 2008, 28(9): 93-97.

[2] 金龙，褚国伟，胡敏强，等．超声波电机速度与定位控制系统[J]．中国电机工程学报，2005, 25(1) :131-136． JIN Long, CHU Guowei, HU Minqiang, et al. The speed and position control system of ultrasonic motor [J]. Proceedings of the CSEE, 2005, 25(1) :131-136.

[3] 蒋春容，胡敏强，金龙，等. 行波型超声波电机定子和转子接触粘滑分布特性[J]. 电工技术学报，2010, 25(12): 48-53. JIANG Chunrong, HU Minqiang, JIN Long, et al. Stick-slip distribution of contact area between stator and rotor in traveling wave ultrasonic motor [J]. Transactions of China Electrotechnical Society, 2010, 25(12): 48-53.

[4] 赵淳生. 超声电机技术与应用[M]. 北京：科学出版社，2007.

[5] 杨淋. 纵扭复合型超声电机的研究[D]. 南京：南京航空航天大学，2010.

[6] 龚书娟. 纵扭复合型超声波电机的若干问题研究[D]. 杭州：浙江大学，2005.

[7] 郭吉丰，魏燕定，刘晓，等. 纵扭复合型超声波电机的力传递模型[J]. 中国电机工程学报，2003, 23(5): 80-85. GUO Jifeng, WEI Yanding, LIU Xiao, et al. Force transferring model of hybrid transducer type ultrasonic motor [J]. Proceedings of the CSEE, 2003, 23(5): 80-85.

[8] 刘锦波，陈永校. 超声波的定转子接触的摩擦传动模型及实验研究[J]. 中国电机工程学报，2000, 20(4): 59-63. LIU Jinbo, CHEN Yongxiao. Investigation on contact model of ultrasonic motor and its experiments [J]. Proceedings of the CSEE, 2000, 20(4): 59-63.

[9] 王剑. 柱状超声波电机的设计理论及控制[D]. 杭州：浙江大学，2009.

[10] MAENO T, TSUKIMOTO T, MIYAKE A. Finite element analysis of the rotor/stator contact in a ring type ultrasonic motor [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, 1992, 39(6):668-674.

[11] MAENO T, BOGY D B. FE analysis and LDA measurement of the dynamic rotor/stator contact in a ring type ultrasonic motor [J]. Journal of Tribology, 1993, 115(4): 625-631.

[12] 曲建俊，周铁英，姜开利，等. 行波超声马达定子和转子接触状态实验研究[J]. 声学学报，2003, 28(3): 217-222. QU Jianjun, ZHOU Tieying, JIANG Kaili, et al. Experimental study of contact state between stator and rotor in a travelling wave ultrasonic motor [J]. Acta Acustica, 2003, 28(3): 217-222.

[13] 蒋春容，胡敏强，金龙，等. 中空环形行波超声波电机有限元接触模型[J]. 东南大学学报(自然科学版)，2014,44(1): 99-103. JIANG Chunrong, HU Minqiang, JIN Long, et al. Finite element contact model of a hollow ring type travelling wave ultrasonic motor [J]. Journal of Southeast University(Natural Science Edition), 2014, 44(1): 99-103.

[14] BEKIROGLU E. Ultrasonic motors: their models, drives, controls and applications[J]. Journal of Electroceramics, 2008, 20(3/4): 277-286.

[15] CHEN Chao, SHE Chongmin. Creep effect analysis at the friction interface of a rotary ultrasonic motor[J]. International Journal of Applied Mechanics, 2015, 7(2): 1550031.

[16] RO J S, JUNG S Y, LEE C G, et al. Survey of a contact model and characteristic analysis method for a travelling wave ultrasonic motor[J]. International Journal of Applied Electromagnetics and Mechanics, 2014, 46(3): 437-453.

[17] 赵淳生，黄卫清. 超声电机的试验研究[J]. 微电机：伺服技术，2003, 36(2): 1-5. ZHAO Chunsheng, HUANG Weiqing. Test research on ultrasonic motors[J]. Micromotor: Servo Technology, 2003, 36(2): 1-5.

Contact model of a novel longitudinal and torsional ultrasonic motor

LI Chong1, LU Cunyue1, MA Yixin1, HUANG Weiqing2

(1. Department of Instrument Science& Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. Precision Driving Lab, Nanjing University of Aeronautics and Astronautics, Nanjing 210000, China)

A novel bonded type longitudinal-torsional piezoelectric motor was presented, including the stator, the rotor, the preloading system, etc. The stator was particularly slotted to form a structure with multi vibrators. The vibrator was constituted by a metal substrate and piezoelectric ceramics, pasted on the outer surface of the metal substrate to simplify the motor structure. Through the reasonable adjustment of design parameters, the resonant frequencies of the first longitudinal vibration mode and the second torsional vibration mode of the stator were adjusted to be as close as possible. Meanwhile, all the vibrators were regulated to the resonance state, which is beneficial to improve the efficiency of the motor. To evaluate the overall performances of the designed motor, a finite element contact model was established to research the contact characteristics of the stator and the rotor. By analysing the static and transient contact process, the pressure distribution on contact areas, contact state, sliding distance, and etc. were all obtained under load free condition. Besides, the speed curve and the output performance of the motor were both acquired. The results of contact analysis show that the longitudinal-torsional motor is working in a multi-surface contact mode actually. The analysis results also show that the contact pressure does not locally concentrate and sliding happens at the contact areas. Finally, according to the design parameters, a prototype motor was fabricated and then the theoretical analysis was verified by experiments.

piezoelectric motor; finite element; contact model; multi-surface contact

国家自然科学基金(11174206)；航空基金(20120657004)；SAST基金(SAST201347)；海洋工程国家重点实验室(1410)

2015-06-18 修改稿收到日期：2015-11-08

李冲 女，博士生，1989年生

鹿存跃 男，博士，副教授，1971年生

TM35

A

10.13465/j.cnki.jvs.2016.22.017