基于流-固耦合算法的跨/超声速曲壁板气动弹性分析
梅冠华, 张家忠, 康 灿
(1. 江苏大学 能源与动力工程学院,江苏 镇江 212013; 2. 西安交通大学 能源与动力工程学院,西安 710049)
基于流-固耦合算法的跨/超声速曲壁板气动弹性分析
梅冠华1, 张家忠2, 康 灿1
(1. 江苏大学 能源与动力工程学院,江苏 镇江 212013; 2. 西安交通大学 能源与动力工程学院,西安 710049)
采用流-固耦合算法研究了曲壁板在跨/超声速气流下的气动弹性特征。首先,给出了曲壁板的Von Kármán几何大变形运动方程,并对其进行了标准有限元离散。然后,简述了流动的控制方程、数值解法、动网格和流-固耦合方式。最后,对曲壁板的气动弹性响应进行了数值模拟和分析。结果表明弯曲造成壁板的初始气动载荷非零,使得其与平壁板的气动弹性特征大相径庭:稳定的曲壁板存在静气动弹性变形;马赫数为2时,曲壁板失稳后,其颤振负向峰值远大于正向峰值,且弯曲高度的增大会诱发混沌型的振动;马赫数为0.8和0.9时,曲壁板仅会发生正向变形;马赫数为1.2时,失稳后曲壁板的颤振中心偏向了负方向。所得结果为高速飞行器的壁板设计和颤振抑制提供了依据,所提算法可推广应用于其它气动弹性问题的数值分析。
壁板颤振;流-固耦合;气动弹性
当前,随着超声速和高超声速飞行器的研发热潮,壁板气动弹性颤振引起了学者们的广泛关注。壁板颤振是指在外部高速气流的冲击作用下飞行器表面的壁板结构所诱发的自激振动现象,这是典型的由惯性力、弹性力和气动力的共同作用而激发的气动弹性问题。该类振动往往具有很强的非线性动力学特性,并将对飞行器的疲劳寿命、飞行性能、飞行安全和乘坐品质带来不利影响。该问题的深入探讨对于高速飞行器的壁板设计、颤振抑制和疲劳寿命估计都具有十分重要的意义[1-2]。
作为经典的气动弹性问题,壁板颤振已被众多学者进行了深入研究,精确高效的数值方法被不断引入,如Galerkin方法[3-4]、有限元方法[5-6]、Rayleigh-Ritz方法[7]、时滞惯性流形方法[8-9]等。所研究的壁板材料也更加贴近实际,如复合材料层合壁板[10]、功能梯度材料壁板[11]等。虽然壁板颤振的研究已经取得了丰硕的成果,然而在这些研究中,气动载荷大多采用简化气动力模型近似表达,如线性/非线性活塞理论[12]、线性化势流理论等,虽然它们便于应用,然而其适用范围和精度都较为有限,尤其无法对非线性效应特别强烈的跨声速流动进行描述。此外,简化气动力理论给出的气动载荷是与固体位移、速度及其偏导数相关的函数,而并非是通过基于流动控制方程的计算流体动力学(CFD)所得出的,因此无法给出流场的细节信息,比如黏性边界层、旋涡、流动分离、激波等,进而无法准确分析流体与固体间的耦合机理。事实上,这些正是壁板颤振定量分析中的开放性问题。
近年来,伴随着计算机软硬件技术的飞速发展,学者们开始尝试将CFD和计算结构动力学(CSD)相结合,发展流-固耦合算法来分析壁板的气动弹性特征,如此不仅能更加精确地反映该问题的本质,而且为跨声速气流下该问题的求解提供了有效手段。DAVIS等[13-14]基于Euler方程的气动力理论,采用流-固耦合算法分析了跨声速气流中的二维壁板颤振问题,并与简化气动力理论所得结果进行了对比,说明了Euler气动理论在分析跨声速壁板颤振问题时的精确性。随后,GORDINER等[15]采用Navier-Stokes方程求解气动载荷,对三维壁板颤振问题进行了研究,发现边界层的存在推迟了颤振的发生。之后,HASHIMOTO等[16]同样采用Navier-Stokes气动力理论分析了跨声速三维壁板颤振问题,在与相关实验结果[17]取得一致的同时,其研究还发现湍流边界层不仅对于颤振可以起到稳定作用,在特定条件下还能引起不稳定效应。国内研究方面,窦怡彬等[18]采用流-固耦合算法对超声速二维壁板颤振特性进行了分析,发现流场内激波和膨胀波的交替变化诱发了壁板的极限环颤振。梅冠华等[19-20]发展了一种基于有限元方法的流-固耦合算法,并用其详细分析了超声速和跨声速二维壁板气动弹性问题,初步分析了流-固耦合结果与简化气动理论所得结果间的差异及其形成原因,其结果与Davis的流-固耦合结果吻合较好。安效民等[21]采用流-固耦合算法对跨/超声速二维壁板颤振进行了详细研究,并对超声速三维壁板颤振进行了探究,与他人结果取得了很好的一致。
目前,在壁板颤振的流-固耦合研究中关注的基本都是平面壁板,事实上,受几何外形影响,飞行器表面的壁板大多呈现为一定程度的弯曲,而并非是理想的平面壁板。从理论上说,该弯曲可以看作是对平面状态的一种扰动,而该扰动的引入往往会给系统的特性带来显著影响。因此,采用流-固耦合算法研究壁板弯曲对其气动弹性特性的影响,这在理论上和实际上都具有重要意义。
为研究初始弯曲对壁板气动弹性特性的影响,也作为先前研究工作的进一步深入,对文献[19-20]中基于有限元方法的流-固耦合算法适当改动,在时域内对曲壁板颤振问题进行了分析。首先,采用Von Kármán几何大变形理论给出了曲壁板运动方程,并用标准有限元方法对该方程进行离散。然后,简述了流动控制方程、求解方法、动网格和流-固耦合方式。最后,采用所发展的流-固耦合算法对超声速和跨声速气流下曲壁板的气动弹性响应行了分析,着重考察了无量纲动压、相对弯曲高度、马赫数、厚度比对系统特性的影响。
1 曲壁板的运动方程及其数值解法
二维曲壁板颤振模型如图1所示:曲壁板置于刚性平面上,其上表面处于沿x方向的高速气流中,下表面对应着空腔。流体的来流速度、马赫数和密度分别为U∞、Ma∞和ρ∞。平板的长度、厚度、单位长度质量、弹性模量和泊松比分别为a、h、ρm、E和μ。平板上表面由流场所施加的气动载荷为p,下表面空腔压力与来流压力相同,皆为p∞。
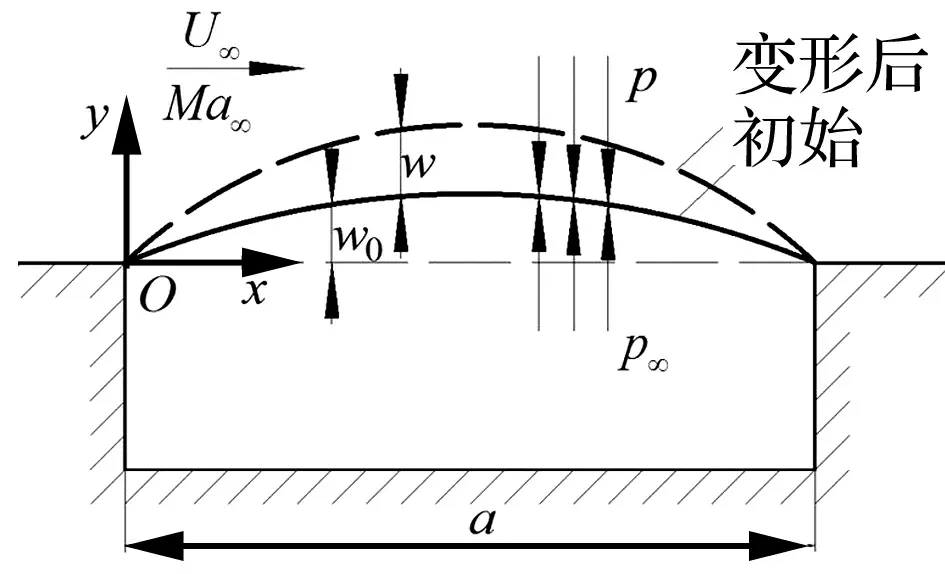
图1 二维曲壁板颤振示意图Fig.1 Schematic of two-dimensional curved panel flutter
假设曲壁板的曲率恒定,应变-位移关系采用Von Kármán几何大变形理论表示,则其控制方程为:
(1)
式中:板的弯曲刚度D=Eh3/[12(1-μ2)],大变形产生的中面拉伸载荷Nx为:
(2)
式中:气动载荷Δp为平板的上下表面压力差,即:Δp=p-p∞。式(1)和式(2)中的Rx为恒定的曲率半径,对最大弯曲高度H≪a的浅壳,可用抛物线方程近似描述其初始形状,即:
(3)
则曲率半径为Rx=a2/8H。壁板两端为简支边界条件,满足w=0,∂2w/∂x2=0。
将壁板沿长度方向均匀划分为N个单元,则单元长度l=a/N。对其中的任意单元,设其两端整体坐标分别为x1和x2,引入坐标变换ξ=(x-x1)/l,将整体坐标[x1,x2]转化为局部坐标[0,1]。在局部坐标系下,采用Hermite单元,则单元上的位移w可以表达为w=Neqe,其中qe={w1θ1w2θ2}T为单元位移向量,Ne=[N1N2N3N4]为单元形函数向量,各形函数的具体表达式为:
N1=1-3ξ2+2ξ3,N2=l(ξ-2ξ2+ξ3),
N3=3ξ2-2ξ3,N4=l(ξ3-ξ2)。
采用标准Galerkin有限元方法对控制式(1)进行变分以及空间离散,可将其转化为关于时间二阶导数的常微分方程组:
(4)
式中:
(5)
式(4)和式(5)中的整体矩阵由单元矩阵组装而成,即:
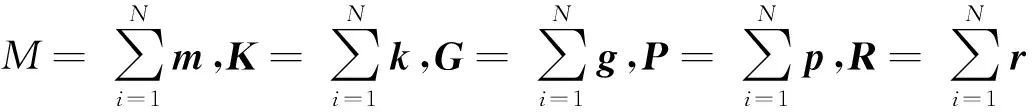
各单元矩阵的具体表达式为:

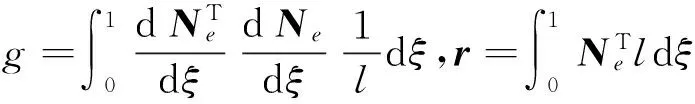
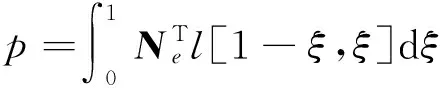
而q={w1,θ1,w2,θ2,…,wN+1,θN+1}T为壁板整体位移。
2 流动控制方程及其数值解法
高速流动采用Euler方程描述,其数值解法为双时间步长推进的特征线分裂有限元方法。
壁板上方流场计算区域及网格剖分情况分别如图2和图3所示,所计算的流动区域呈半圆形,其半径为25倍的壁板弦长。圆弧上为远场边界条件,壁板上游和下游皆为刚性壁面,在无黏流动中将其法向速度设为0即可,流-固交界面受壁板运动的影响,将其给定为(u-us)·n=0,其中u为流体速度,us为壁板运动速度,n为壁板节点的法向量。激波捕捉方法为基于压力二阶导数的方法。
采用分块结构化网格剖分计算区域,子域1的上边界为与弯曲壁板相对应的弯曲边界,这样便于生成高质量的网格,流场网格共计5 881个节点和11 520个三角形单元。
该部分的详细叙述可参阅文献[19-20]。
3 动网格及流-固耦合方式
随着流-固交界面的运动,流场内部的计算网格也需进行处理,由于壁板运动仅发生在y方向上,故仅需将壁板节点的位移在子域1内沿着y方向均分即可,这样既能保证网格质量又不会在动网格处理上耗费大量的计算时间。
流-固耦合的方式为松耦合,在每个时间步流体传递气动载荷给壁板,壁板则传递位移和速度给流体,从而实现流动和结构间的双向耦合。关于动网格和流-固耦合方式的更详细描述可参考文献[19-20]。

图2 流场计算区域(非等比例绘制)Fig.2 Computational domain for fluid field

图3 流场网格Fig.3 Mesh for flow field
4 数值模拟结果和分析
采用FORTRAN语言实现上述算法,算法和代码的验证工作已经在文献[19-20]中完成,故不再赘述。
4.1 超声速气流下的壁板响应
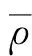
若H/h=0,则曲壁板退化为平壁板。动压λ较小时,壁板将保持平面稳定状态,当动压λ逐渐增大并越过临界值λcr,系统将发生Hopf分岔,由平面稳定状态转化为极限环振动状态,且极限环振幅随λ的增大而增大,颤振近乎正负对称。
与平壁板不同,受壁板弯曲的影响,H/h>0的曲壁板上下表面的初始压力差值不为零,即其初始气动载荷非零,因此曲壁板将偏离其初始形状,寻求新的静态气动弹性平衡位置。以H/h=1和λ=200为例,系统的位移时间历程如图4所示,在初始气动载荷作用下,历经瞬态响应的壁板达到了新的稳态变形位置,并在该位置上和气动载荷达到了静态平衡状态。动压λ对壁板稳态变形和气动载荷的影响如图5所示:壁板变形以向下凹陷为主,仅后部略微向上拱起,随着λ的增大最大弯曲位置逐渐后移且弯曲高度逐渐减小;在壁板前缘和尾缘附近存在两个明显的激波,前缘激波的强度随着λ的增大而减弱,而后缘激波几乎未受影响,压力的整体分布则随着λ的增大而趋向均匀。即,壁板变形和气动力之间的相互作用减弱了壁板的弯曲程度,也使得气动载荷的分布更加趋于均匀。

图4 曲壁板的静态气动弹性变形历程(H/h=1,λ=200)Fig.4 Time history of static aeroelastic deformation for a curved panel (H/h=1, λ=200)
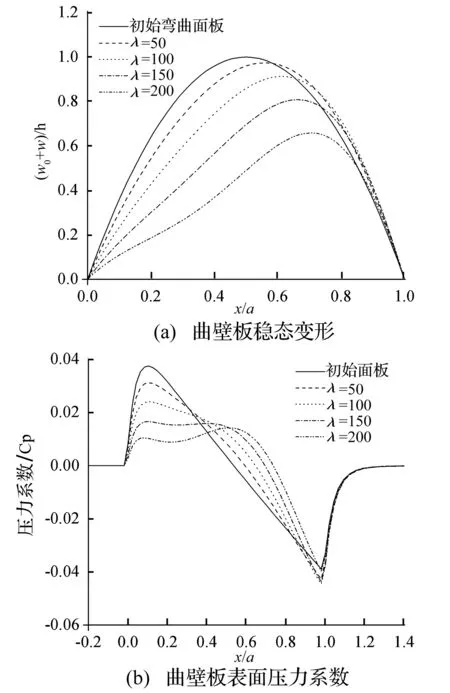
图5 动压对曲壁板静气动弹性特性的影响 (H/h=1)Fig.5 Effect of dynamic pressure on static aeroelastic behavior of curved panels (H/h=1)
当动压λ进一步增大并跨过临界值λcr=248,系统发生了Hopf分岔,表现为极限环颤振。图6给出了在λ=300下系统的响应,经过大约10个周期的瞬态振荡壁板进入到了稳定的颤振状态,该振动并不是关于中性面正负对称的,负向峰值的绝对值大约为正向峰值的两倍,而平壁板的振动则近乎是上下对称的。这是因为曲壁板是在下凹的静态气动弹性变形位置上失稳发生颤振的,振动的中心应在该稳态变形位置附近,因此振动呈现出了负向峰值较大的特性。动压λ对颤振峰值的影响如图7所示,颤振负向峰值的绝对值较大,并随着λ的增大而增大,颤振的正向峰值较小,且几乎保持在一个稳定值上,图7中还用虚线标出了颤振的中点,可以清晰地发现其位于壁板失稳前静态气动弹性变形随λ变化曲线的延长线上,即恰是由于此平衡位置的失稳才导致了曲壁板的非对称型颤振。
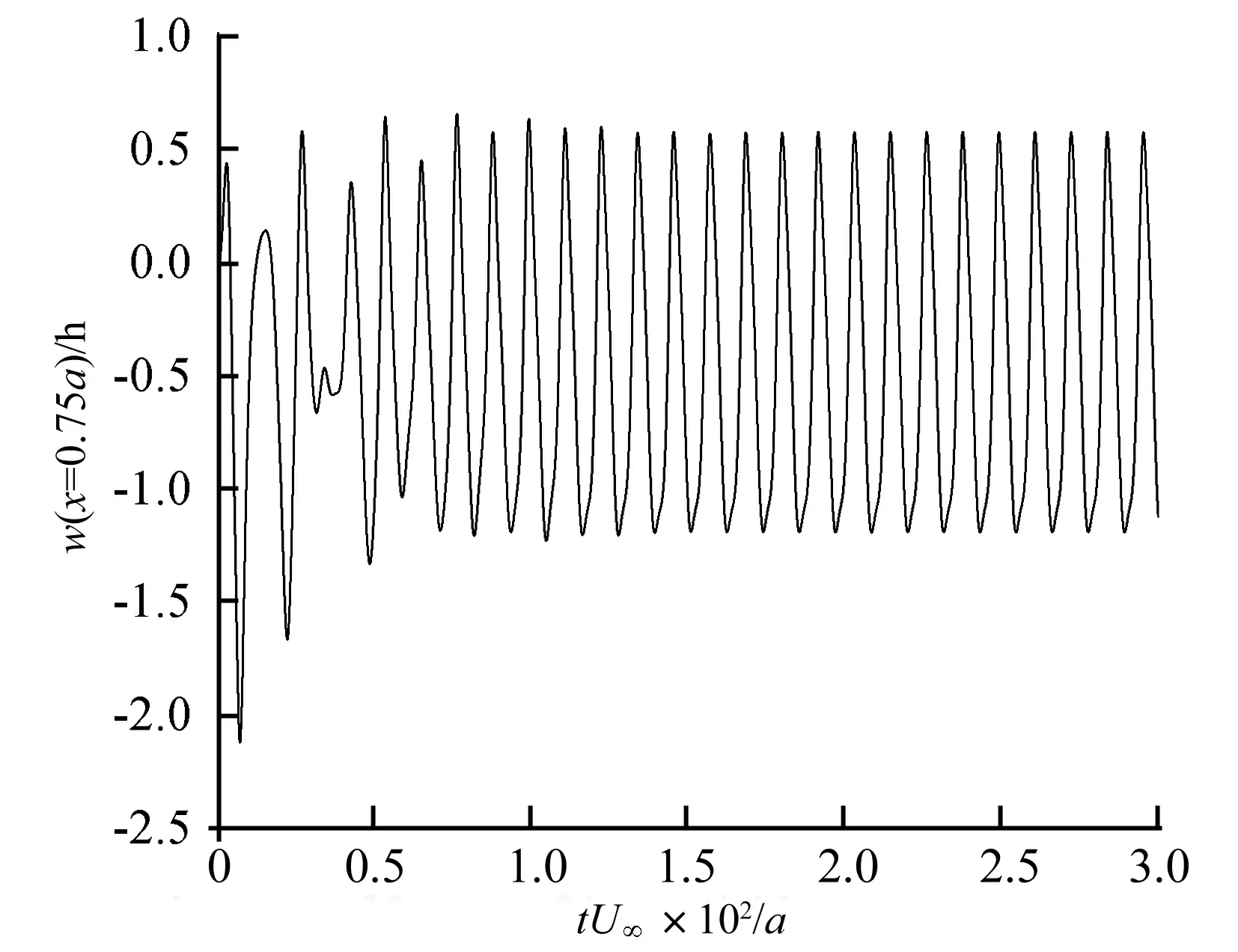
图6 曲壁板颤振的位移时间历程 (H/h=1,λ=300)Fig.6 Time history of displacement for flutter of a curved panel (H/h=1, λ=300)
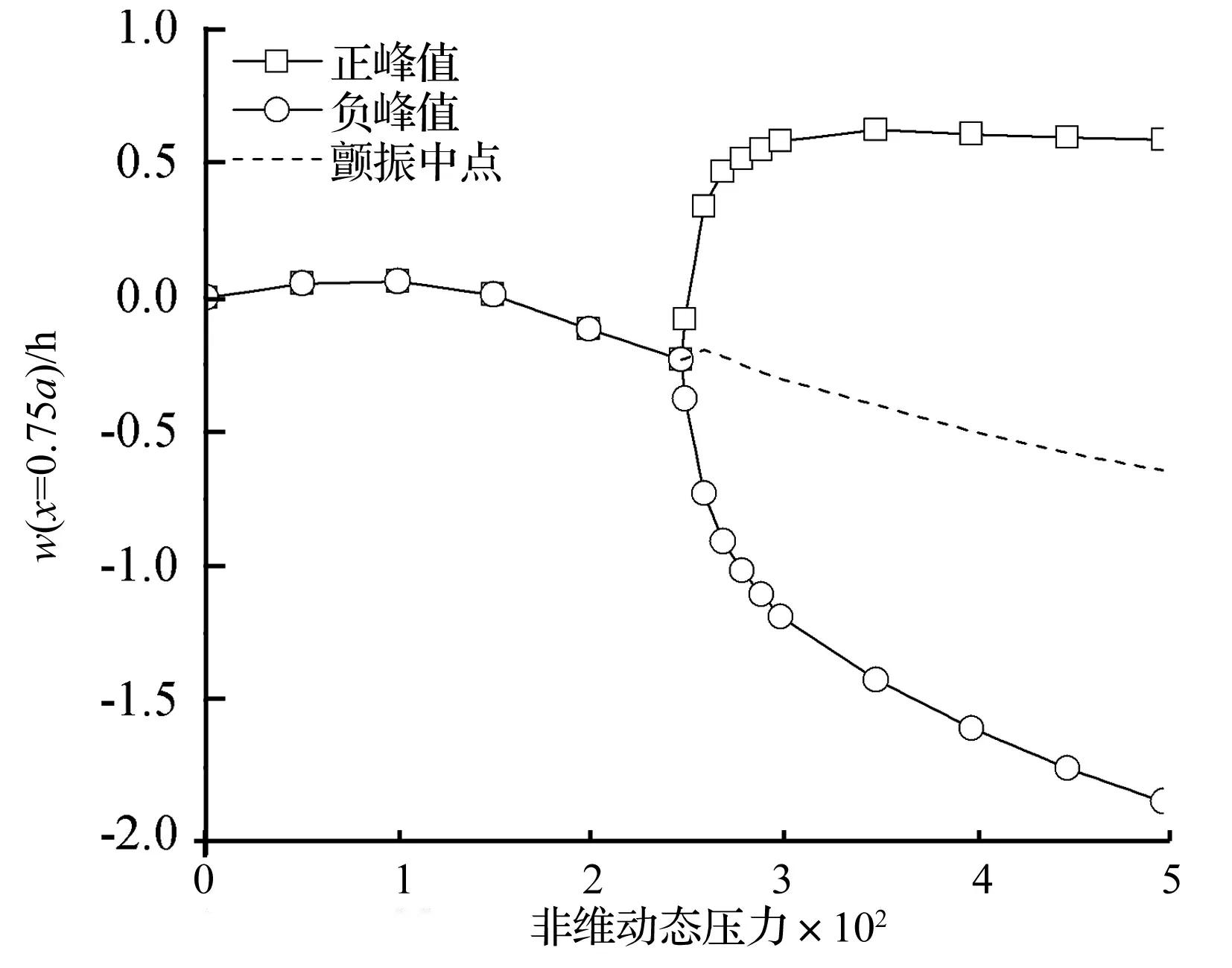
图7 动压对曲壁板颤振正负峰值的影响 (H/h=1)Fig.7 Effect of dynamic pressure on positive and negative peak amplitudes of curved panel flutter (H/h=1)
进一步,增大壁板的弯曲高度至H/h=2,其稳态变形特性与H/h=1的曲壁板相同,不再重复。随着动压的增大并越过临界值λcr=196,壁板突然进入到了混沌运动状态,图8(a)给出了λ=200时壁板的稳态响应,其表现为看似杂乱无章实则又有一定规律的运动状态,同样地,壁板的负向运动要比正向运动更为剧烈。将无量纲时间步长变换为真实物理时间步长,并对壁板的稳态响应进行频谱分析,所得结果如图8(b)所示,可见该振动包含了众多的频率组分。作为定量判定混沌的指标,Lyapunov指数描述了系统临近轨道间的距离在长时间演变过程中指数发散程度的强弱。采用C-C算法计算了最佳延迟时间和重构维数,对壁板稳态响应时间序列进行了相空间重构,并在此相空间上使用Wolf所提出的算法[22]得到了系统的最大Lyapunov指数,为0.088大于0,故可认为系统处于混沌运动状态。随着λ的继续增大,系统又出现了稳态的周期振荡,如图9所示的λ=400时壁板的稳态响应。可见初始弯曲作为非线性扰动对系统的特性可造成显著影响,随弯曲高度的增大壁板更加复杂的运动形式被不断激发出来。
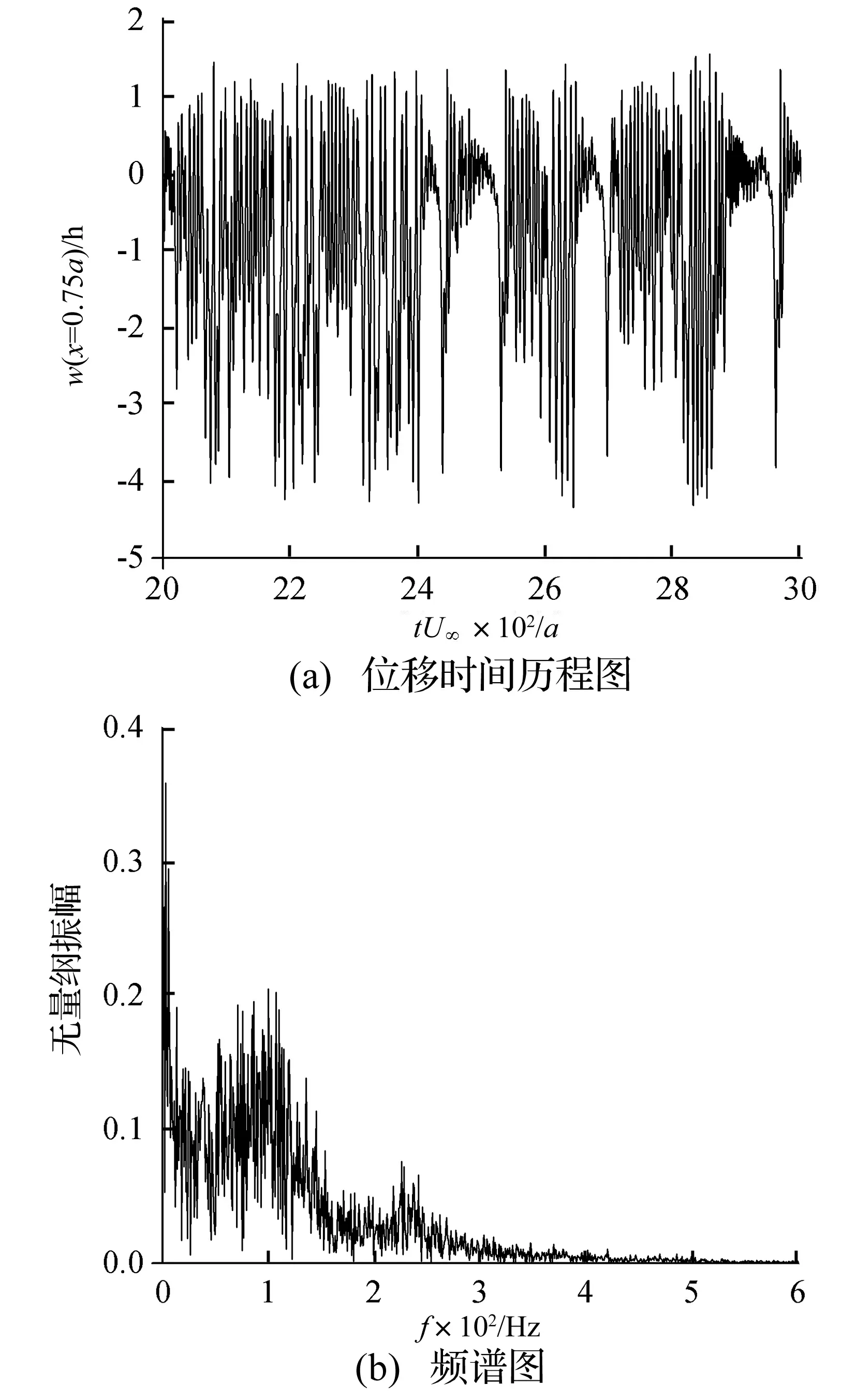
图8 混沌运动状态的曲壁板 (H/h=2,λ=200)Fig.8 Chaotic motion of a curved panel (H/h=2, λ=200)

图9 曲壁板周期振动的位移时间历程 (H/h=2,λ=400)Fig.9 Time history of displacementfor a periodic oscillation of curved panel (H/h=2, λ=400)
4.2 跨声速气流下的壁板响应
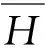
对于H/h=0的平壁板,在Ma∞=0.8或0.9时,随h/a的减小壁板由平面稳定状态转化为屈曲状态,依据不同的初始条件到达正向或是负向的稳定变形位置。变形量随着h/a的减小而增大,这是因为壁板越薄,其刚度越小,越容易发生变形。Ma∞=0.8时壁板正负屈曲近乎对称,而Ma∞=0.9时正向变形要略大于负向变形。
对于H/h>0的曲壁板,以H/h=1和h/a=0.002为例,在Ma∞=0.8时壁板的稳态变形和压力系数分布如图10所示,由于壁板上下表面的压力差值为两端高中间低的对称分布形式,且以负值为主,故壁板表现为左右对称的上凸变形。接下来,考察了相对厚度h/a和相对弯曲高度H/h对壁板稳态变形的影响,并与平壁板的正向屈曲结果进行了对比,将其汇总在图11中。与平壁板相比,曲壁板仅会出现上凸的稳态变形,而并不会发生下凹的稳态变形,这是因为初始气动载荷以负值为主,迫使壁板运动到了向上的稳态变形位置。另外,曲壁板的变形量要小于平壁板,且稳态变形随着弯曲高度的增大而减小,这说明曲壁板抵抗稳态变形的能力要强于平壁板。由于气动载荷随着Ma∞的增加而增强,故Ma∞=0.9下的变形要大于Ma∞=0.8下的变形。
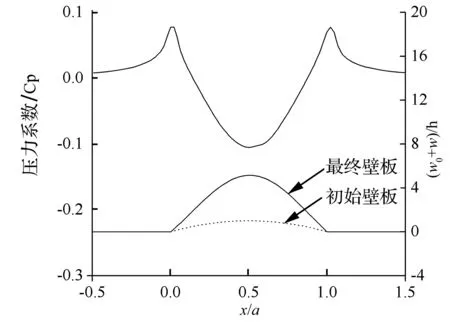
图10 曲壁板稳态变形和气动载荷分布 (海平面铝板,Ma∞=0.8,h/a=0.002,H/h=1)Fig.10Stable deformation and aerodynamic load of a curved panel (aluminum panel at sea level, Ma∞=0.8, h/a=0.002, H/h=1)
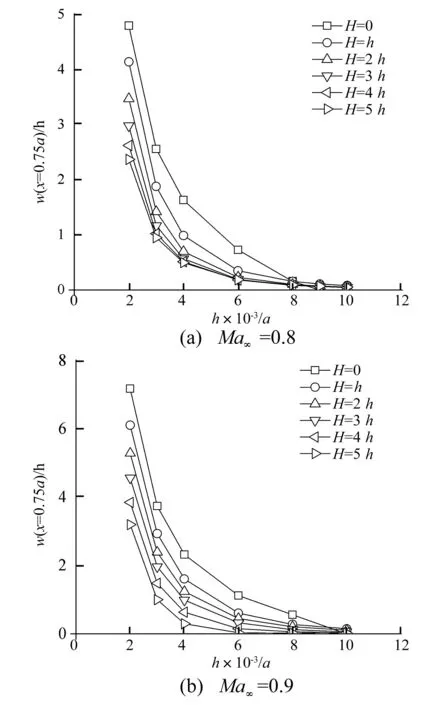
图11 h/a和H/h对曲壁板稳态变形的影响 (海平面铝板)Fig.11 Effect of h/a and H/h on stable deformation of curved panels (aluminum panel at sea level)


图12 曲壁板的静气动弹性变形和压力系数 (Ma∞=1.2,H/h=1,λ*=40)Fig.12 Static aeroelastic deformation and pressure coefficient of a curved panel (Ma∞=1.2, H/h=1, λ*=40)
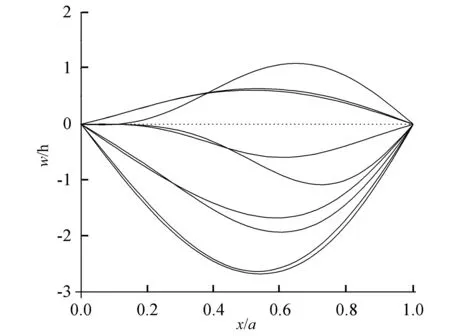
图13 一个周期内的壁板瞬态变形 (Ma∞=1.2,H/h=1,λ*=100)Fig.13 Transient deformation of panel in one period (Ma∞=1.2, H/h=1, λ*=100)

图14 极限环振幅随动压变化 (Ma∞=1.2,H/h=1)Fig.14 Effect of dynamic pressure on limit cycle oscillation amplitude (Ma∞=1.2, H/h=1)
5 结 论
采用基于特征线分裂有限元方法的流-固耦合算法,分析了超声速和跨声速气流作用下二维曲壁板的气动弹性特性。着重考察了马赫数、相对弯曲高度和动压对系统特性的影响,通过对数值模拟结果进行分析,所得主要结论如下:
(1)与平壁板不同,由于壁板弯曲造成的初始气动载荷不为零,曲壁板将偏离其初始状态,达到静态气动弹性变形位置。
(2)在超声速气流下,曲壁板失稳后出现了极限环颤振,且与平壁板近乎对称的振动不同,由于曲壁板是从静态气动弹性平衡位置失稳进入颤振的,故其颤振的负向峰值的绝对值远大于正向峰值。随着壁板弯曲高度的增加,其非线性特性增强,混沌形式的颤振被激发了出来。
(3)在跨声速气流下,当马赫数为0.8和0.9时,曲壁板仅可发生正向的静态气动弹性变形,而不会像平壁板那样出现正负屈曲变形,且变形量随弯曲高度的增大而减小,随马赫数的增大而增大。当马赫数为1.2时,曲壁板失稳后表现为极限环颤振,且与超声速情况类似,曲壁板的负向振动更为剧烈。
作为初步研究,流动采用Euler方程描述,并未考虑气动加热效应,且着重考察了壁板响应特性。未来将采用Navier-Stokes方程,引入湍流模型和壁板导热方程,发展流-固-热耦合求解算法,对该耦合系统内的物质输运、动量迁移和能量传递特征进行深入剖析。
[1] MCNAMARA J J, FRIEDMANN P P, POWELL K G, et al. Aeroelastic and aerothermoelastic behavior in hypersonic flow [J]. AIAA Journal, 2008, 46(10): 2591-2610.
[2] LAMORTE N, FRIEDMANN P P. Hypersonic aeroelastic and aerothermoelastic studies using computational fluid dynamics [J]. AIAA Journal, 2014, 52(9): 2062-2078.
[3] DOWELL E H. Nonlinear oscillations of a fluttering plate [J]. AIAA Journal, 1966, 4(7): 1267-1275.
[4] DOWELL E H. Nonlinear flutter of curved plates [J]. AIAA Journal, 1969, 7(3): 424-431.
[5] OLSON M D. Finite element approach to panel flutter [J]. AIAA Journal, 1967, 5(12): 226-227.
[6] OLSON M D. Some flutter solutions using finite element [J]. AIAA Journal, 1970, 8(4): 747-752.
[7] YE W L, DOWELL E H. Limit cycle oscillation of a fluttering cantilever plate [J]. AIAA Journal,1991,29(11): 1929-1936.
[8] 梅冠华, 张家忠, 席光. 基于时滞惯性流形的二维平面壁板非线性气动弹性分析 [J]. 振动与冲击,2012,31(10): 141-146. MEI Guanhua, ZHANG Jiazhong, XI Guang. Nonlinear aeroelastic analysis of a two-dimensional panel based on inertial manifolds with delay [J]. Journal of Vibration and Shock, 2012, 31(10): 141-146.
[9] MEI Guanhua, ZHANG Jiazhong, WANG Zhuopu. Numerical analysis of panel flutter on inertial manifolds with delay [J]. Journal of Computational and Nonlinear Dynamics-Transactions of ASME, 2013, 8(2): 021009.
[10] GRAY C E, MEI C. Large amplitude finite element flutter analysis of composite panels in hypersonic flow [J]. AIAA Journal, 1993, 31(6): 1090-1099.
[11] 李凯伦, 张家忠. 功能梯度材料薄板的热气动弹性数值分析方法及特性研究 [J]. 宇航学报, 2013, 34(9): 1177-1186. LI Kailun, ZHANG Jiazhong. Numerical analysis method and aerothermoelastic behaviors of temperature dependent functional graded panels [J]. Journal of Astronautics, 2013, 34(9): 1177-1186.
[12] ASHLEY H, ZARTARIAN G. Piston theory—a new aerodynamic tool for the aeroelastician [J]. Journal of the Aeronautical Science, 1956, 23(12): 1109-1118.
[13] DAVIS G A, BENDIKSEN O O. Unsteady transonic two-dimensional Euler solutions using finite elements [J]. AIAA Journal, 1993, 31(6): 1051-1059.
[14] DAVIS G A. Transonic aeroelasticity solutions using finite elements in an arbitrary Larangian-Eulerian formulation [D]. Los Angeles:University of California, 1994.
[15] GORDINER R E, FITHEN R. Coupling of a nonlinear finite element structural method with a Navier-Stokes solver [J]. Computers & Structures, 2003, 81(2): 75-89.
[16] HASHIMOTO A, AOYAMA T. Effects of turbulent boundary layer on panel flutter [J]. AIAA Journal, 2009, 47(12): 2785-2791.
[17] MUBLSTEIN L, GASPERS P A, RIDDLE D W. An experimental study of the influence of the turbulent boundary layer on panel flutter[R]. NASA Paper No. TN D-4486, 1968.
[18] 窦怡彬, 徐敏, 蔡天星, 等. 基于CFD/CSD耦合的二维壁板颤振特性研究 [J]. 工程力学, 2011, 28(6): 176-188. DOU Yibin, XU Min, CAI Tianxing, et al. Investigation of a two-dimensional panel flutter based on CFD/CSD coupling method [J]. Engineering Mechanics, 2011, 28(6): 176-181.[19] 梅冠华, 杨树华, 张家忠, 等. 用于跨/超声速壁板颤振精确分析的流-固耦合有限元算法 [J]. 西安交通大学学报, 2014, 48(1): 73-83. MEI Guanhua, YANG Shuhua, ZHANG Jiazhong,et al. A fluid-structure coupling algorithm based on finite element method for precise analysis of transonic and supersonic panel flutter [J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 73-83.
[20] MEI Guanhua, ZHANG Jiazhong, XI Guang, et al. Analysis of supersonic and transonic panel flutter using a fluid-structure coupling algorithm[J]. Journal of Vibration and Acoustics-Transactions of ASME, 2014, 136(3): 031013.
[21] 安效民, 胥伟, 徐敏. 非线性壁板颤振分析 [J]. 航空学报, 2015, 36(4): 1119-1127. AN Xiaomin, XU Wei, XU Min. Analysis of nonlinear panel flutter [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1119-1127.
[22] WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov exponents from a time series [J]. Physica D: Nonlinear Phenomena, 1985, 16(3): 285-317.
Aeroelastic analysis of curved panels in transonic/supersonic airflowbased on a fluid-structure coupling algorithm
MEI Guanhua1, ZHANG Jiazhong2, KANG Can1
(1. School of Energy and Power Engineering, Jiangsu University, Zhenjiang 212013, China; 2. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
A fluid-structure coupling algorithm was used to analyze the aeroelastic behaviors of curved panels in transonic/supersonic airflow. According to the Von Karman’s large deformation theory, the governing equation of curved panels was presented, and it was discretized by the standard finite element method. The governing equations of fluid, numerical method, moving mesh technique and fluid-structure coupling way were introduced briefly. Numerical simulations and analyses were carried out to study the aeroelastic behaviors of curved panels. The results demonstrate that the curvature causes nonzero initial aerodynamic load on panels, which brings about greatly different aeroelastic features for curved panels compared with flat panels. Static aeroelastic deformations exist on curved panels in steady state. At Mach number of 2, the asymmetric flutter will be born as curved panels lose their stability. As the curvature height increases, the chaotic flutter can be induced. At Mach number of 0.8 and 0.9, curved panels bear only positive aeroelastic deformation. At Mach number of 1.2, with the stability lost, curved panels flutter more violently in the negative direction. The results obtained could guide the panel design and flutter suppression for high performance flight vehicles. The presented algorithm could be extended to numerically analyze other aeroelastic problems.
panel flutter; fluid-structure coupling; aeroelasticity
国家973计划(2012CB026002);国家科技支撑计划(2013BAF01B02);江苏高校优势学科建设工程资助项目;江苏大学高级人才科研启动基金(15JDG155)
2015-09-16 修改稿收到日期:2015-11-09
梅冠华 男,博士,1984年11月生
张家忠 男,博士,讲师,教授,博士生导师,1968年1月生
O323
A
10.13465/j.cnki.jvs.2016.22.009

