集装箱运输车自装卸装置关键结构设计与分析

司癸卯,汪程浩,李圆圆

(长安大学 道路施工技术与装备教育部重点实验室,陕西 西安 710064)



集装箱运输车自装卸装置关键结构设计与分析

司癸卯,汪程浩,李圆圆

(长安大学 道路施工技术与装备教育部重点实验室,陕西 西安 710064)

吊臂结构是集装箱运输车自装卸装置的关键装卸部件.在合理简化的基础上,运用Pro/E软件与ANSYS Workbench的无缝对接,对两种危险工况下的吊臂进行了有限元分析,得到了吊臂的应力、应变云图,完成了强度、刚度校核,提出了结构修改建议.结果表明:吊臂结构设计合理,满足刚度、强度使用要求.

自装卸装置; 吊臂; 有限元分析; 强度分析

集装箱自装卸运输车是一种能够实现不同规格集装箱双侧自动化装、卸、运功能的特种车辆,由牵引车和半挂车两部分组成.牵引车上配有液压泵站,提供液压动力.自装卸装置成对安装于半挂车上,实现集装箱自装自卸.自装卸装置设计采用伸缩臂式吊装机构,体积小，结构紧凑,回转半径小,能在码头、堆场及各种不同复杂环境下实施灵活装卸搬运,具有极高的工作效率.本文采用三维Pro/E软件对自装卸装置进行设计实体建模,并结合有限元软件ANSYS Workbench对吊臂进行了强度设计分析.

1 自装卸装置结构及作业工况

1.1 自装卸装置结构

自装卸装置主要由下摆臂、伸缩臂、底座、支腿、变幅油缸和锁紧机构等部分组成,结构简图如图1所示.简图展示了自装卸装置由未工作时90°位置至起吊重物时位置的状态[1].

图1 自装卸运输车机构简图Fig.1 Diagram of self-handling transport vehicle

吊装机构包含伸缩臂总成与下摆臂总成两部分,采用一级油缸伸缩,简称为吊臂.

1.2 吊臂的作业工况分析

在自装卸集装箱的过程中,吊臂主要有以下几大工况[2],如图2所示.

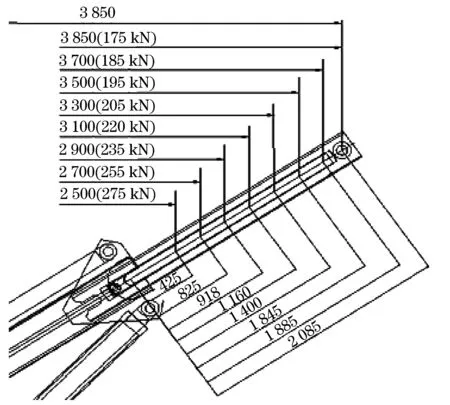
图2 吊臂变幅工作量示意图(单位:mm)Fig.2 Schematic diagram of boom amplitude workload (unit:mm)

(1) 变幅油缸工作,伸缩臂完全伸出但未变幅装卸时,伸缩臂伸缩2 065 mm,整个机构受力主要来源于伸缩臂与下摆臂的自重及其附件,这时伸缩臂所受的载荷较小.

(2) 变幅油缸工作,伸缩臂完全伸出装卸集装箱,摆动变幅3 850 mm,此时伸缩臂与水平面的夹角最小,为最小仰角34°.平稳起吊,集装箱重量作用于伸缩臂的吊杆位置处,此工况下设计的单臂额定起吊量为17.5 t,此时整个伸缩臂所承受的弯矩为673 750 N·m,这是装卸作业的一种危险作业工况,此时伸缩臂受力最大,强度和刚度要求最高,工作稳定性最差.

(3) 变幅油缸工作,伸缩臂未完全伸出起吊集装箱货物时,起吊集装箱货物重量未超过设计的额定载荷,起吊工作安全平稳,伸缩臂及下摆臂强度刚度以及工作稳定性均能满足要求.

(4) 变幅油缸工作,伸缩臂伸出435 mm,摆动变幅2 500 mm时起吊集装箱货物,此工况下设计的单臂额定起吊量为27.5 t,此时整个伸缩臂所承受的弯矩为687 500 N·m,这是装卸作业另一种危险作业工况,需核算该工况下伸缩臂及下摆臂的设计强度、刚度以及工作稳定性.

1.3 危险工况确定

根据自装卸装置的装卸量及工况分析,得出吊臂最不利的两大工况:

工况1:装卸仰角最小，为33.9°时,伸缩臂全伸,变幅幅距3 850 mm,起吊17.5 t货物.工况2:装卸仰角最小,为33.9°时,伸缩臂全缩,变幅幅距2 500 mm,起吊27.5 t货物.

若在危险工况下吊臂的刚度和强度满足要求,则证明整个作业环境下吊臂的状态是安全的.

2 三维实体模型建立与简化

为方便设计分析,本文基于实际装卸工况,对吊臂支撑的边界样式、载荷变化形式做了合理必要的简化[3].简化包含以下几方面:

(1) 起吊货物重量均匀施加于吊杆,伸缩臂臂体重力也均匀施加于模型上;

(2) 对于小的倒角、圆角、圆孔等不影响整体应力分布的结构进行忽略;

(3) 整个伸缩臂结构间均匀焊接连接,分析时不考虑焊缝处的材料特性的变化;

(4) 忽略制造误差、焊接偏差、壁厚偏差等;

(5) 将基座、变幅油缸等结构视为刚体,忽略其对伸缩臂变形的影响.

简化后的两种工况吊臂实体模型如图3，4所示.

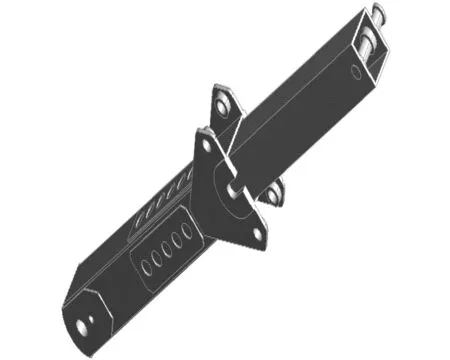
图3 工况1吊臂实体模型Fig.3 Boom model of condition one

3 ANSYS Workbench分析前处理

吊臂结构主体设计采用HG70,许用应力为393.3 MPa.通过新创建材料属性,完成各项参数设定,接触采用的是默认Bonded接触.

3.1 网格划分

有限单元法求解时不同的节点个数决定了单元的计算精度[4].有限单元法的节点划分通过网格划分来完成.网格划分稀疏,无法达到分析精度,计算误差较大;网格划分紧密,则会增加电脑CPU的计算时间,增高计算机硬件的配备要求[5].

图4 工况二下摆臂实体模型Fig.4 Downswing arm model of condition two

在求解开始时,Meshing平台会自动生成默认的网格,在采用默认网格的前提下,检查网格质量并进行调整,并对结构进行局部细化调整,控制多零部件接触面组划分的精度.工况1下,整个吊臂结构共划分节点73873个,实体单元网格37761个,如图5所示.细化后,模型复杂结构部位网格划分密度大,划分的质量较高[6].工况2下,主要考虑下摆臂结构的强度,故对下摆臂进行单独建模分析,参数调整设置,危险截面细化后,共划分节点数58631个,实体单元网格30076个,如图6所示.

图5 吊臂网格划分效果Fig.5 Effect of boom mesh generation

3.2 载荷及边界条件施加

在工况1的情况下,伸缩臂装卸量为218 750 N,直接作用于吊杆,伸缩臂与水平面夹角为33.9°,下摆臂铰接点、双侧变幅油缸铰接点均采用销轴连接,需约束3点位置3个方向的平移自由度以及2个方向的转动自由度,释放绕销轴回转中心的转动自由度,完成载荷与支撑的施加[7].

图6 下摆臂网格划分效果Fig.6 Effect of downswing arm mesh generation

在工况2的条件下,下摆臂端面所受的切向力为69.3 kN,伸缩臂伸出435 mm时产生的附加弯矩为177.4 kN·m,下摆臂边界条件约束同工况1一致.

4 有限元的模拟结果及分析

分别对工况1，2条件下AWB 软件中的Solution模块进行求解,计算分析结果包含等效应力云图和总变形云图两部分,得出结构模型的受力分布情况及变形量，如图7—10所示.

图7 吊臂等效应力云图Fig.7 Effective stress cloud chart of boom

图8 吊臂变形云图Fig.8 Deformation cloud chart of boom

根据图7所示,在工况1的条件下,整个吊臂的结构设计及加强处理较合理,没有明显的应力集中现象(应力云图显示大部分为安全区域).在伸缩臂与下摆臂贴合的剪切面处,存在较大的应力,该工况下应力最大值为328.06 MPa,小于材料的许用应力393.3 MPa.因此可以判定伸缩臂结构强度能够满足使用要求.另外,除了最大受力面外,下摆臂变幅油缸安装耳板孔处也存在一定的应力集中,工况1环境下作用应力分布区域较小,在工况2中分析下摆臂受力时需注意此处的结构强度.

在工况2条件下,下摆臂的结构应力远小于材料的许用应力393.3MPa,整个结构强度能满足使用要求，如图9所示.其中下摆臂变幅油缸销轴孔截面为危险截面,应力值约80～90MPa,变幅油缸支撑销轴孔处产生的最大应力为120.21MPa,下摆臂结构产生的最大偏移变形为0.104 48mm,如图10所示.这个数量级的变形量不足以对下摆臂造成影响,可以忽略不计.综上考虑,我们认为车工况2条件下,整个吊臂的结构强度满足要求.

图9 下摆臂等效应力云图Fig.9 Effective stress cloud char of downswing arm

图10 下摆臂变形云图Fig.10 Deformation cloud char of downswing arm

由强度分析可得,额定工况下吊臂作业,伸缩臂与下摆臂均存在局部应力集中区域.伸缩臂最大应力产生于最大伸出量2 065 mm时与下摆臂的剪切面,下摆臂最大应力则产生于变幅油缸与下摆臂安装腹板的剪切面,其中销轴安装孔内部存在局部应力集中.但是不论伸缩臂还是下摆臂,其最大应力或最大变形均小于材料的许用应力和扰度.由此可以验证,正常工作时,整个吊臂臂体的强度和刚度均能满足使用要求,在伸缩臂的两端以及下摆臂的下端,强度仍有较大的富裕量.

5 结构分析改进建议

综上所述,在保证吊臂装卸工作安全、可靠的条件下,为适当提升吊臂的结构强度,优化结构,减少吊臂重量,降低材料消耗,提出如下的建议:

(1) 调整伸缩臂的截面尺寸形状.初步设计时,伸缩臂纵向截面形状和尺寸完全一致,而最大应力截面只发生于同下摆臂接触的剪切面,虽然不同装卸伸缩量对应剪切面不同,但工况1为整个伸缩臂最危险受力工况,故此,我们可以考虑在设计装配结构允许的情况下,保证伸缩臂纵向截面的宽度尺寸,适当加大其高度尺寸,而且也可以设计成伸缩臂头尾两端采用不同截面高度的箱形臂体.这样,在提高伸缩臂危险截面强度的前提下,不仅可以减轻伸缩臂整体的重量,降低制造加工成本,而且通过伸缩臂头尾不同截面高度的设计,还可以使材料特性充分利用.

(2) 应力集中部位可以增焊加强筋板.整个吊臂应力集中范围较小,因此可以在应力集中区域增加加强筋设计焊接,局部加强筋板焊接并不会带来整个吊臂重量的提升,但是可以有效保证结构的强度和刚度.此外,在工况2的条件下,下摆臂与变幅油缸的连接腹板销轴孔结构有一定的局部应力集中,可以根据结构条件适当加大腹板厚度或者采用较厚的加强筋达到支撑要求.

(3) 基于上述修改方案,建立合适的吊臂结构数学模型,进行优化设计,以便得到合理的伸缩臂、下摆臂箱架结构及参数.

6 结论

本文对自装卸装置吊臂进行了设计分析,基于设计装载量及实际作业工况,分析出吊臂结构工作的两大危险工况,并将两大工况下合理简化后的实体模型导入ANSYS软件,完成吊臂结构的仿真分析,得出等效应力云图及最大变形云图,验证吊臂的设计刚度及强度,并针对结构提出改进建议.结果表明:伸缩臂下摆臂的危险截面的最大应力值为328.06 MPa,最大变形位移11.764 mm,刚强度均能满足使用要求.

[1] 贾超.基于ANSYS的汽车起重机起重臂参数化设计研究[D].沈阳:沈阳建筑大学,2011.

JIA Chao.Design & research of mobile crane boom based on ANSYS[D].Shenyang:Shenyang Jianzhu University,2011.

[2] 罗清雨.可伸缩变幅带式输送机伸缩臂结构强度有限元优化设计研究[D].南京:南京理工大学,2005.

LUO Qingyu.Design & research of telescopic boom structure strength finite element optimization of scalable amplitude conveyor[D].Nanjing:Nanjing University of Science and Technology,2005.

[3] CHAMPION E R.Finite element analysis in manufacturing engineering[M].NewYork:McGraw-Hill,Inc,1992.

[4] BEERMAN H J.The analysis of commercial vehicle structures [M].London:Mechanical Engineering Publication Limited,1989.

[5] SHEPHARD M S,BAEHMANN P L,GRICE K R.Automatic finite element modeling:geometry control for direct models[J].Engineering Computations,1987,4(2):119-125.

[6] 纪爱敏,彭铎,刘木南,等.QY25K型汽车起重机伸缩吊臂的有限元分析[J],工程机械,2003(1):19-21.

JI Aimin,PENG Duo,LIU Munan,et al.The finite element analysis of QY23K mobile crane[J].Construction Machinery,2003(1):19-21.

[7] 蒋红旗.高空作业车作业臂有限元结构分析[J].机械研究与应用,2004,17(6):68-69.

JIANG Hongqi.The finite element structure analysis of aerial platform boom[J].Research & Apply of Machinery,2004,17(6):68-69.

[8] 化学工业部.机械设计手册[M].第3版.北京:化学工业出版社,1996.

Ministry of Chemical Industry.Mechanical design handbook[M].3rd ed.Beijing:Chemical Industry Press,1996.

Design and analysis on key structures of self-handling equipment for container transporters

SI Gui-mao,WANG Cheng-hao, LI Yuan-yuan

(Key Laboratory for Highway Construction Technique and Equipment of Ministry of Education, Chang'an University, Xi'an 710064, China)

Due that the crane boom structure is a key handling component for the self-handling equipment of container transporter, the boom finite element analysis is first conducted based on rationale simplification. By using Pro/ETM and ANSYS WorkbenchTM under two dangerous working conditions, the stress and strain contours are then obtained to check the strength and rigidity of crane boom. Finally, the structural modification is proposed. Therein, it is indicated that the strength and rigidity meet the demands on rationale boom structure design.

self-handling equipment; crane boom; finite element analysis; strength analysis

司癸卯(1963-),男,副教授,工学博士.E-mail:smart@chd.edu.cn

TH 247

A

1672-5581(2016)04-0337-05