基于Hoff理论的金属复合屋面板夹层壳单元

黄 莉,邓 华

(1. 浙江财经大学 房地产与工程管理系,浙江 杭州 310018; 2. 浙江大学 空间结构研究中心,浙江 杭州 310058)



基于Hoff理论的金属复合屋面板夹层壳单元

黄 莉1,2,邓 华2

(1. 浙江财经大学 房地产与工程管理系,浙江 杭州 310018; 2. 浙江大学 空间结构研究中心,浙江 杭州 310058)

针对大跨度建筑屋盖结构常用的聚氨酯泡沫夹芯金属复合屋面板,根据修正后的Hoff型夹层板理论,建立简便、有效的八结点矩形夹层壳单元.以一块矩形屋面板为例,分别采用分层实体单元、夹层体单元和八结点矩形夹层壳单元模拟.数值结果显示,八结点矩形夹层壳单元模拟的屋面板在静荷载作用下的变形形式与精细的分层实体单元模型相同,且两者变形基本接近；基本振型与精细的分层实体单元模型相同,自振频率较接近.表明采用该夹层壳单元能够有效地模拟聚氨酯夹芯金属复合屋面板的静、动力特性.

金属复合屋面板；Hoff型夹层板；夹层壳单元；八节点单元

抗风设计是大跨度屋盖结构设计要点之一,当前屋盖结构抗风设计和分析中通常忽略屋面板的作用,假设屋面板的刚度无穷大.目前大跨度屋盖结构多采用金属复合屋面板,通常由压型金属薄板作为上、下面层,中间填充聚氨酯泡沫塑料、岩棉或玻璃纤维棉等保温材料,采用一定的成型工艺形成的夹层板.金属复合屋面板的刚度非常有限,并非假设的无穷大,且聚氨酯、岩棉等夹芯材料均是工业上应用较广的阻尼材料.屋面板在将表面风压传递给主体结构的过程中,有限刚度和夹芯层阻尼会对风荷载的脉动特性产生影响[1],最终影响结构风致振动效应的计算结果.合理估计金属复合屋面板对大跨度屋盖结构风致振动效应的影响,可以优化屋盖结构的抗风设计,节约屋盖结构的造价.分析屋面板对屋盖结构风致振动的影响效应,必须将金属复合屋面板纳入屋盖结构风致振动效应的有限元计算中.金属屋面板为多层材料构成的复合板,若直接对屋面板的各层分层模拟,则各层材料均需单独建模和划分单元,建模阶段繁琐复杂.为了保证计算精度,屋面板的单元划分需要较细,加之大跨度结构体量一般都较大,模拟屋面板的单元数目相当多.为了提高建模效率和计算收敛速度,建立能够模拟金属复合屋面板静、动力特性的复合夹层单元成为必然.本文在前期工作的基础上,根据修正的非对称Hoff型夹层板理论[2-3],针对聚氨酯泡沫夹芯金属复合屋面板建立八结点夹层壳单元.

1 基本假定

1.1 Hoff型夹层板

Hoff型夹层板理论的基本假定[2]如下.1)小变形且各层间无相对滑移；2)各层沿高度方向不可压缩；3)各层的横向位移假定不变,仅考虑反对称变形；4)考虑上、下面层的抗弯性能,面层在平面内的切应变为零；5)夹芯层只承受横向剪切作用.

1.2 金属复合屋面板假定

图1 夹层板Fig.1 Sandwich panel

上、下面层金属板的材料、厚度不同,屋面板不具有传统Hoff型夹层板的对称性,中面上的点在xy平面内的位移不为零,分别为u0、v0.屋面板的变形采用直线假定,即变形前垂直于中面的直线变形后为直线但不再垂直于中面.采用3个广义位移φx、φy、w确定夹层板中任意一点的全部位移.φx、φy为上、下面层中面上对应点的连线在变形后的转角,如图2所示.

图2 金属复合屋面板变形图Fig.2 Deformation of metal composite roof panel

根据Hoff理论的基本假定及变形假定,上、下面层和夹芯层中各点位移分别表示如下[3],其中+、-、c分别表示上面层、下面层及夹芯层.

2 有限单元构建

针对复合夹层板有限单元的构建研究[4-9]不少,但基本都是针对较薄的复合板.本文基于夹层板的Hoff型理论,结合聚氨酯夹芯金属屋面板的解析理论[3],构建较厚的屋面板复合夹层壳单元.

2.1 基本定义

单元定义在夹芯层中面上,为八结点的矩形夹层壳单元.如图3所示,x-y-z为局部坐标系,x、y向分别为压型方向和顺压方向；s-t-r为自然坐标系,s、t轴为2个相互垂直的切线方向,r为法线方向.

该单元的每个结点具有5个自由度u、v、w、θx、θy,在荷载作用下夹层板发生变形,变形后的矩形单元如图4的虚线所示.

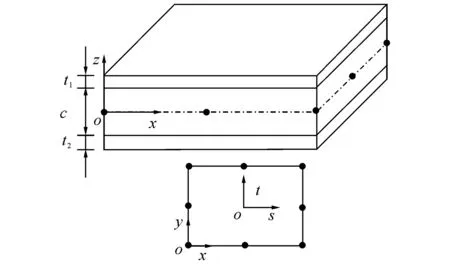
图3 八结点矩形单元Fig.3 Eight-node rectangular element

图4 自由度定义Fig.4 Definition of freedom

2.2 位移表示

单元中结点i的位移向量为[ui,vi,wi,θxi,θyi]T(i=1,…,8),屋面板中任意一点的位移采用结点位移表示为

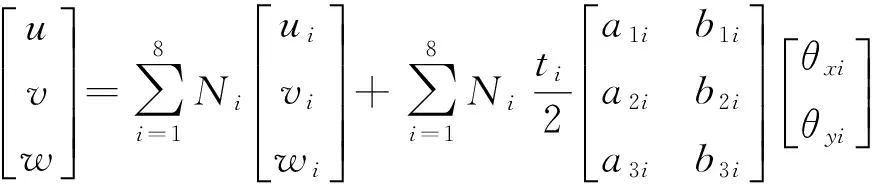
(1)

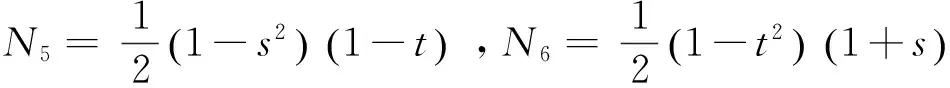
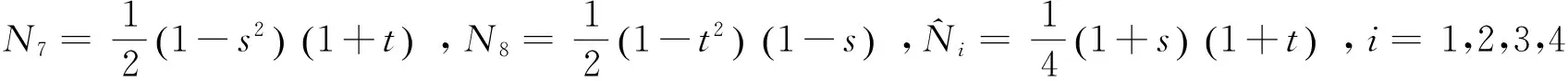
写为矩阵形式为

u=Nd.

(2)

式中：u=[u,v,w]T为位移向量；N为形函数矩阵；d为结点位移矩阵,

d=[u1,u2,u3,u4,u5,u6,u7,u8].

2.3 应力表示

夹芯层的应力、应变分别为

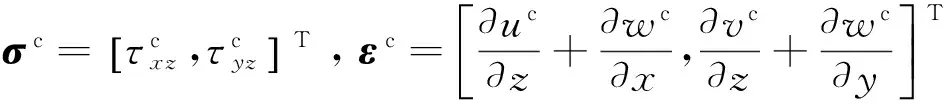
结合Hooke定理得到夹芯层的应力与结点位移的关系为

σc=DcBcd.

(3)

式中：Bc为夹芯层的应变矩阵,

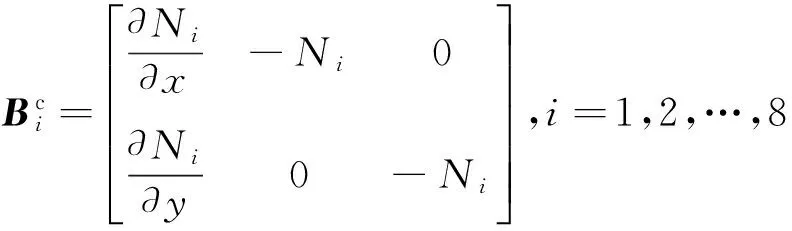
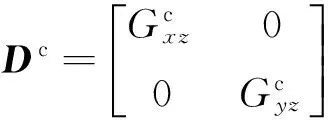
σ±=D±B±d.

(4)

式中：

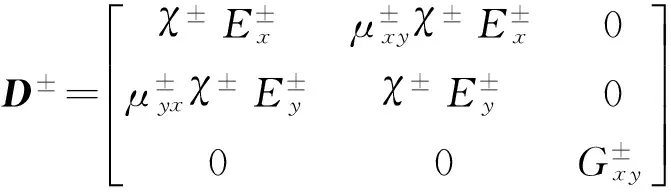
其中

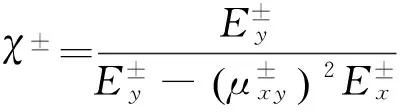
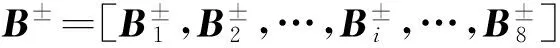
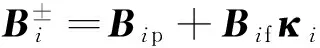
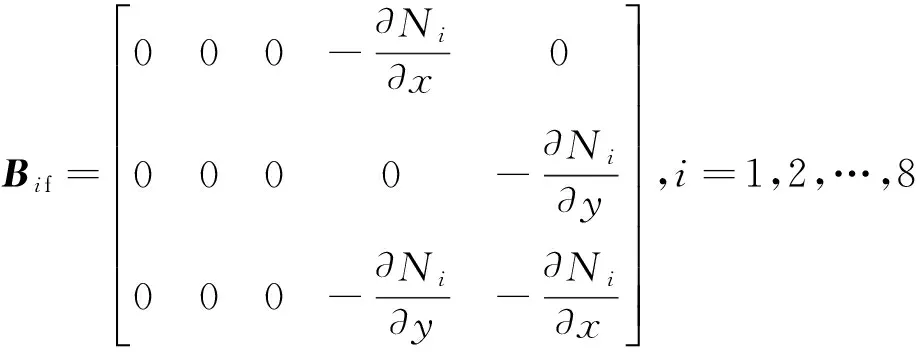
2.4 平衡方程

根据基本假定可知,考虑上、下面层的抗弯刚度,夹芯层只承受横向剪切作用,则单元承受的力和弯矩可以表示为

(5)

式中：

单元无阻尼的动力方程为

(6)

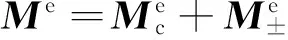
如图5所示为整体坐标X-Y-Z与局部坐标x-y-z的关系.x轴与X轴、Y轴、Z轴间的夹角分别为α1、α2、α3,y轴与X轴、Y轴、Z轴间的夹角分别为β1、β2、β3,z轴与X轴、Y轴、Z轴间的夹角分别为γ1、γ2、γ3.

X-Y-Z坐标系下单元的结点位移矩阵为

dd=Td.

(7)

式中：T为坐标转换矩阵,

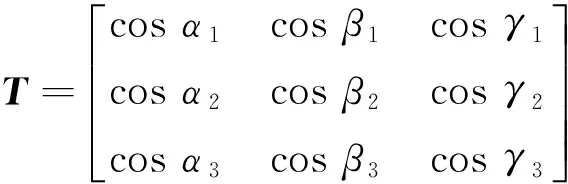
将所有单元在整体坐标系中的质量矩阵、刚度矩阵和外荷载向量组集成屋面板的整体质量矩阵、刚度矩阵和荷载向量,代入到屋面板的动力方程为

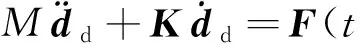
(8)

式中：M为屋面板的整体质量矩阵,Md=TTMT；K为整体刚度矩阵,Kd=TTKT；F为外荷载向量.

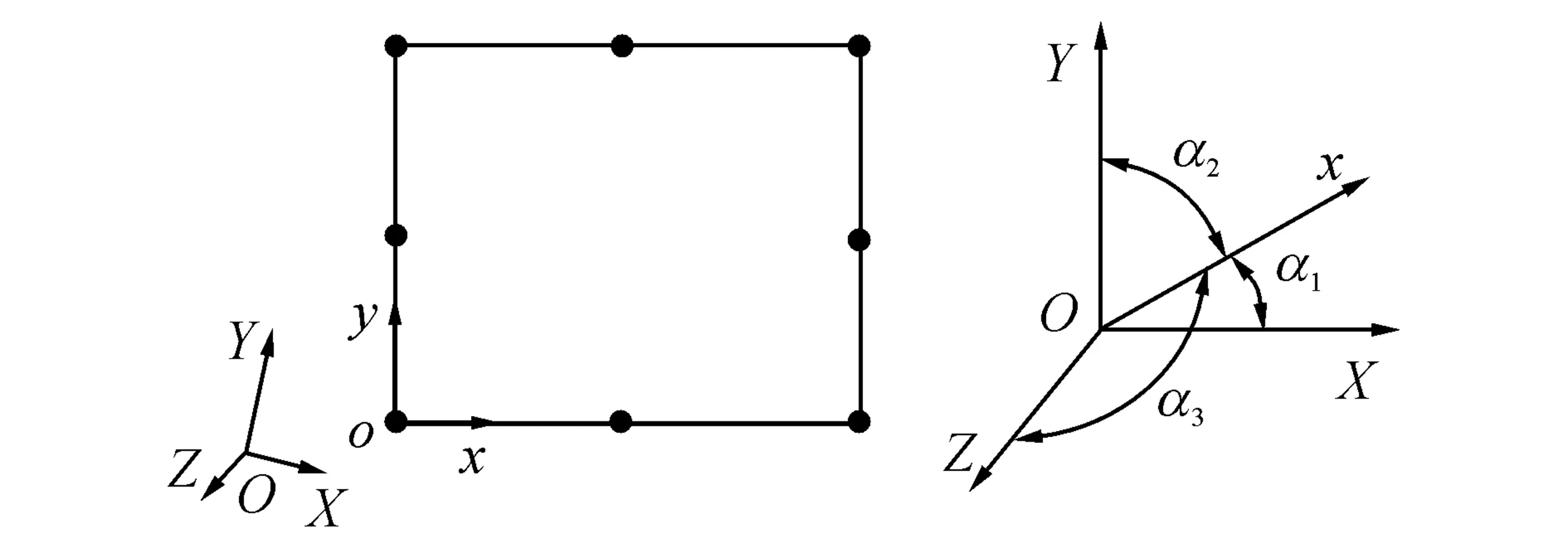
图5 整体坐标与局部坐标关系Fig.5 Relationship between global coordinate and local coordinate

3 数值算例

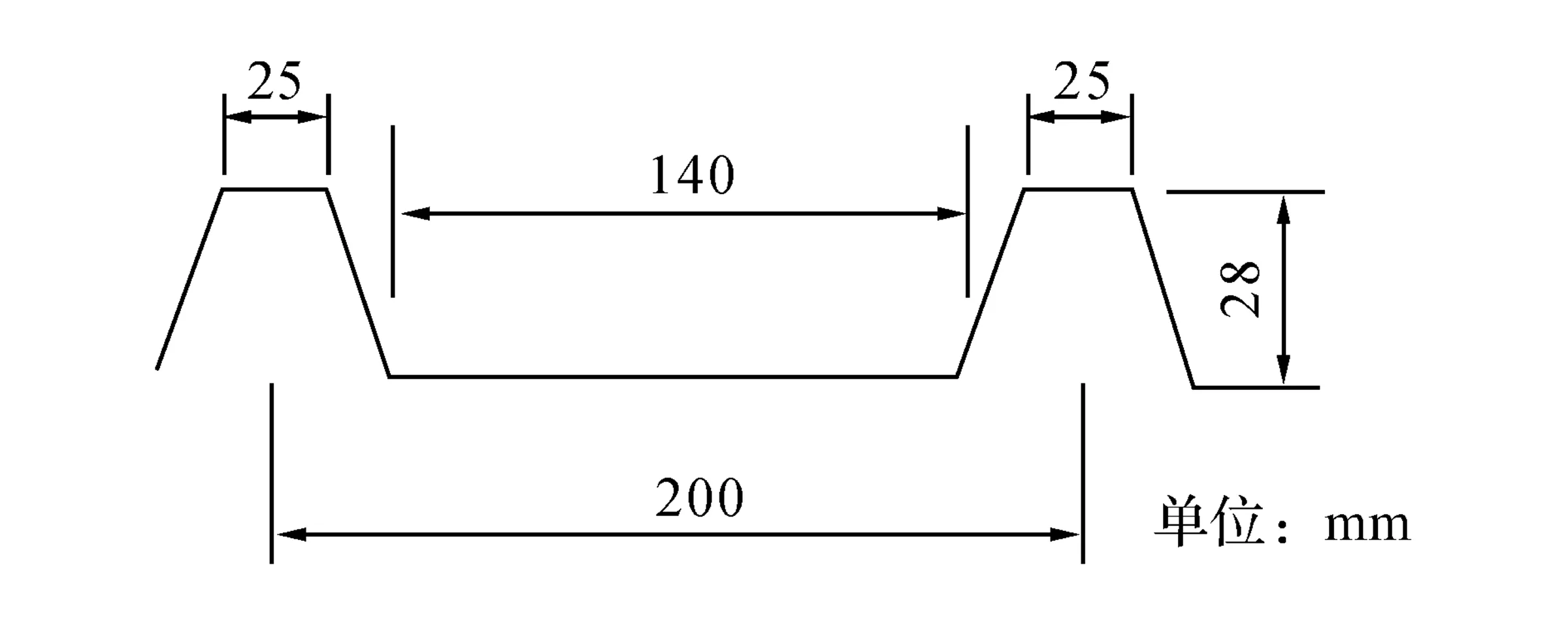
图6 上面层压型钢板尺寸Fig.6 Sizes of top corrugated steel sheet

3.1 模型参数

取一块长(檩距)为2.6 m、宽为1.0 m、两对边固定约束的聚氨酯夹芯金属屋面板进行数值分析.屋面板上、下面层均为0.6 mm厚的钢板,上面层为压型钢板,压型尺寸如图6所示；下面层采用平钢板,聚氨酯夹芯层的厚度取为60 mm.钢材的密度为7 850 kg/m3,弹性模量为206×106 MPa,泊松比为0.3.将压型钢板按文献[10]的方法等代为平板后的等效弹性常数,见表1.表中，Geff为压型板等代为平板后的等效切变模量.聚氨酯夹芯层的材料力学参数按文献[11]选取.

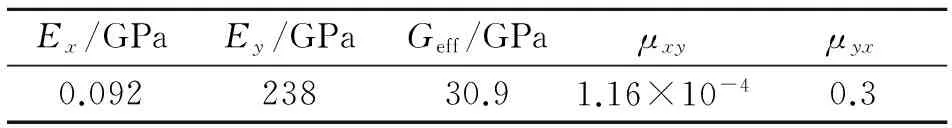
表1 等代平板的等效弹性常数

为了验证八结点矩形夹层壳单元的正确性,采用3种不同的有限元模型进行对比分析.利用通用有限元软件ANSYS建立该屋面板的有限元模型,如图7所示.

1) 模型1.分层实体模型,上、下面层采用弹性壳单元(shell63单元)进行模拟,将压型尺寸建入模型中,夹芯层采用实体单元(solid45单元),两者节点采用耦合连接,约束两对边所有节点的线位移.

2) 模型2.夹层体单元模型(solid46单元),压型板采用等代平板,约束条件与模型1相同.

3) 模型3.八结点矩形夹层壳单元模型利用外部接口程序实现,压型板采用等代平板,约束两对边所有节点的线位移和转动位移.

图7 三种有限元模型Fig.7 Three different finite element models

模型1为金属屋面板的实际模型,即最精细的有限元模型,而模型2和模型3是简化后的有限元模型.

3.2 结果分析

3.2.1 静力特性 为了考察3种模型在荷载作用下变形及应力分布是否相同,对模型的上表层逐步施加均布荷载.如图8所示为相同均布荷载作用下3种模型的变形图.可以看出,模型1和模型3相同,模型2与其他两个模型存在差异.为了保证3种模型的边界条件相同,均将模型两长边方向节点的所有位移施加约束.模型2的单元为分层实体单元,上、下面层尽管较薄但认为是实体；模型1和模型3中上、下面层为壳单元,因此图8中模型2的变化与另外2个模型不同,这是由于模型2无法模拟边界处转角的约束,说明采用分层实体单元模拟金属屋面板与实际不符合.

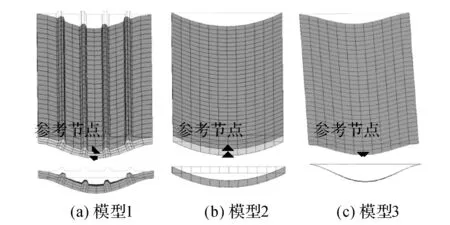
图8 3种模型的变形图Fig.8 Deformation of three finite element models

如表2所示为3种模型短边中点的z向位移.其中模型1和模型2分别取上、下面层对应处的位移,d11、d12为模型1的上、下面层对应处位移,d21、d22为模型1的上、下面层对应处位移,d1、d2为上、下面层位移的平均值,以该平均值作为参考值.

表2 z向位移

从表2可以看出,模型1和模型2中上、下面层的z向位移不完全相同,上面层的位移略大于下面层.除初始加载(0.1 kN/m2)外,模型1上、下面层位移差与均值的百分比为0.506% ～ 0.675%,模型2为0.533% ～ 0.710%,上、下面层的位移差是由于模型1和模型2考虑了各层的横向压缩造成的.同时,模型2和模型3的位移小于模型1,这是由于模型2和模型3先将压型板等代为平板,无法反映屋面板金属层的压型对屋面板变形的影响,所以两者的位移小于模型1.模型2和模型3参考位移与模型1参考位移的差值百分比分别约为-5%和-5.0%～-6.0%.

3.2.2 动力特性 通过考察3种模型的模态频率和各阶振型来比较动力特性,3种模型的前10阶模态频率值见表3.可以看出,3种模型的各阶模态频率不完全相同,模型3的频率基本高于模型1和模型2；随着阶数的增大,三者的模态频率差距越来越小.除前两阶外,模型3与模型1的频率差值百分比较模型2小.

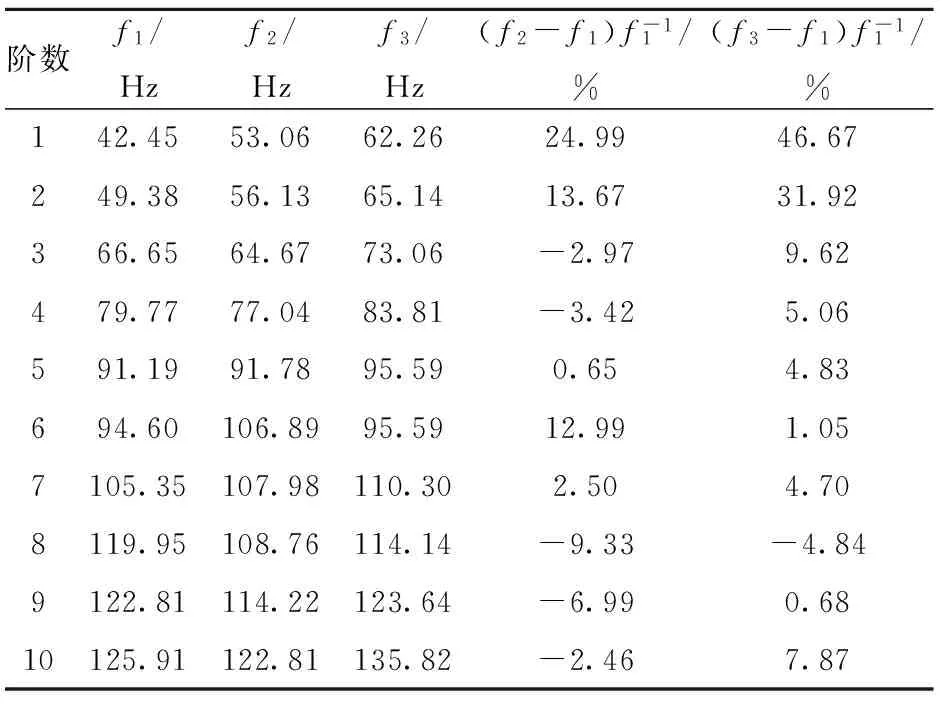
表3 前10阶模态频率

图9 第1、4阶模态振型图Fig.9 Modal shape of mode 1,4

如图9所示为第1、第4阶振型图.3种模型的前3阶振型相同,从第4阶开始,3种模型的振型出现明显差异,模型1的振型开始表现出反对称形式,而模型2和模型3的振型只有对称形式,这是由上面层压型所导致的.

4 结 论

(1)根据修正后的Hoff型夹层板理论,建立八结点矩形夹层壳单元.该单元位于夹芯层的中面,每个结点具有3个线位移和2个转动位移.

(2)通过八结点矩形夹层壳单元与分层实体模型、夹层体单元模型的有限元对比分析发现,采用该新建单元模拟的屋面板在静荷载作用下的变形形式、基本振型与精细的分层实体模型相同,且两者的变形和自振频率基本接近.

(3)八结点矩形夹层壳单元的建模过程简单,单元总数目不到分层实体模型单元总数目的1/3,对存储的需求量少.

[1] 邓华, 黄莉, 王宸. 聚氨酯夹芯屋面板的风致动力性能分析[J]. 浙江大学学报: 工学版, 2013, 47(12): 2125-2131． DENG Hua, HUANG Li, WANG Chen. Analysis on wind-induced dynamic behaviors of polyurethane sandwich roof panels [J]. Journal of Zhejiang University: Engineering Science, 2013, 47(12): 2125-2131．

[2] 中国科学院力学研究所. 夹层板壳的弯曲、稳定和振动[M]. 北京: 科学出版社, 1977．

[3] 黄莉, 邓华. 基于Hoff理论的金属复合屋面板基本方程[J]. 浙江大学学报: 理学版, 2015, 42(2): 147-152． HUANG Li, DENG Hua. The fundamental equations of metal composite roof panel based on Hoff theory [J]. Journal of Zhejiang University: Science Edition, 2015, 42(2): 147-152．

[4] ZABARAS N, PERVEZ T. Viscos damping approximation of laminated anisotropic composite plates using the finite element method [J]. Computer Methods in Applied Mechanics and Engineering, 1990(81): 291-316．

[5] 吴晖. 含压电致动器的四结点矩形复合材料夹层板单元[J]. 工程力学, 2004, 21(4): 156-161． WU Hui. A four node rectangular element for composite sandwich plates with piezoelectric actuators [J]. Engineering Mechanics, 2004, 21(4): 156-161．

[6] 李大永,罗应兵,彭颖红,等. 实体壳单元及其在动力显式有限元方法中的应用[J]. 上海交通大学学报, 2006, 40(10): 1663-1666． LI Da-yong, LUO Ying-bing, PENG Ying-hong, et al. The solid shell element and its application in the dynamic explicit finite element method [J]. Journal of Shanghai Jiaotong University, 2006, 40(10): 1663-1666．

[7] MOREIRA R A S, RODRIGUES J D, FERREIRA A J M. A generalized layer wise finite element for multi-layer damping treatments [J]. Computational Mechanics, 2006, 37(5): 426-444．

[8] VICTOR L. An asymptotic theory of sandwich plates [J]. International Journal of Engineering Science, 2010, 48(3): 383-404．

[9] 张波, 沈火明. 基于Matlab的壳体有限元分析[J]. 重庆理工大学学报: 自然科学, 2010, 24(12): 77-81． ZHANG Bo, SHEN Huo-ming. Finite element analysis of shell based on Matlab [J]. Journal of Chongqing University of Technology: Natural Science, 2010, 24(12): 77-81．

[10] 周学军, 张之峰. 压型钢板等效为正交各向异性板的有限元分析[J]. 钢结构, 2010, 25(8): 35-37． ZHOU Xue-jun, ZHANG Zhi-feng. Finite element analysis of the corrugated steel sheet equated to orthotropic plate[J]. Steel Construction, 2010, 25(8): 35-37．

[11] 黄莉, 邓华, 王宸. 金属复合屋面板用硬质聚氨酯泡沫的力学性能[J]. 建筑材料学报, 2014, 17(2): 320-325． HUANG Li, DENG Hua, WANG Chen. Study on mechanical properties of rigid polyurethane foam core used in metal composite roof panels[J]. Journal of Building Materials, 2014, 17(2): 320-325．

Hoff theory-based sandwich shell element for metal composite roof panel

HUANG Li1,2, DENG Hua2

(1.DepartmentofRealEstateandEngineeringManagement,ZhejiangUniversityofFinanceandEconomics,Hangzhou310018,China; 2.SpaceStructuresResearchCenter,ZhejiangUniversity,Hangzhou310058,China)

Metal composite roof panel with polyurethane foam core is often used as the roof covering of large-span structures. A simple and effective eight-node rectangular sandwich shell element was established for the polyurethane foam sandwich panel based on the amended theory of the Hoff-type sandwich panel. A rectangular roof panel was employed as an example. Layered solid elements, sandwich solid element and eight-node rectangular sandwich shell element were respectively used to simulate the roof panel. Results reveal that the deformation form of the eight-node rectangular element model is the same as the accurate layered solid element model, and their deformation values are similar. The basic vibration modes are as same as accurate layered solid element model, and vibration frequency is approximated. Results indicate that the sandwich shell element can effectively simulate the static and dynamic characteristic of polyurethane sandwich composite metal roof．

metallic composite roof panel; Hoff-type sandwich panel; sandwich shell element; eight-node element

2014-12-31. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

浙江省自然科学基金资助项目(LY14E080015).

黄莉(1987-)，女，讲师，博士，从事钢结构和空间结构的研究.ORCID：0000-0002-1929-0357.E-mail：huangli@zufe.edu.cn 通信联系人：邓华，男，教授，博导. ORCID：0000-0002-0792-0518.E-mail：denghua@zju.edu.cn

10.3785/j.issn.1008-973X.2016.01.007

O 342; TU 393

A

1008-973X(2016)01-0041-07