基于四元数的机械手姿态定向控制

黄水华,江 沛,韦 巍,项 基,彭勇刚

(浙江大学 电气工程学院,浙江 杭州 310027)



基于四元数的机械手姿态定向控制

黄水华,江 沛,韦 巍,项 基,彭勇刚

(浙江大学 电气工程学院,浙江 杭州 310027)

为了有效利用机械手关节自由度,提出机械手的姿态定向控制方法,即保持机械手末端朝向,而允许工具绕某一朝向轴的旋转自运动.四元数法在姿态控制上不存在奇异点,因而采用四元数的方法,实现机械手的姿态定向控制.通过构建姿态定向误差的四元数表述形式,引入姿态定向误差反馈,构造李雅普诺夫函数,证明了其全局稳定性.采用定向控制后,机械手由原先的六维度控制任务转变为五维,从而多出一个冗余度,可以用于提高机械手在避免关节限位、奇异点以及提升可操作度等方面的能力.实验证明,采用该方法能够良好地实现姿态定向误差收敛,验证了理论上的稳定性证明,获得比姿态定位控制更好的运行效果.

定向控制；姿态控制；四元数；机器人运动学

工业机械手关节自由度一般不小于6,姿态控制功能是该类机械手所必须具备的.在传统的机械手姿态控制中,要求机械手的工具姿态完全确定,即姿态定位控制.在一些机械手应用场合中,机械手的姿态控制不需要实现定位控制,如工业机械手焊接允许焊枪绕其轴线旋转运动,乒乓球机械手击球允许球拍面的轴向旋转运动.该类姿态控制为定向控制,即要求机械手工具的某一轴向跟随规划方向运动.定向控制任务的维数为五维(三维位置以及两维姿态).对于关节冗余的机械手,一般可以采用冗余控制算法实现机械手的运动规划和运行控制.

姿态的表述方法有很多种,包括特殊正交群SO(3)、欧拉角、修正罗德里格参数、四元数法等.Luh等[1]将特殊正交群用于机械手姿态控制[1],然而在Lin[2]的工作中,姿态误差形式[1]被证明其不具备全局稳定性.修正罗德里格参数表达的姿态运动范围受限[3],较少应用于机械手姿态控制,部分工作见文献[4,5].欧拉角采用最少的3个参数表达姿态[6-8].采用欧拉角表述的姿态反馈存在奇异情况,无法保证全局稳定性[9].欧拉角计算复杂,三参数的姿态表述必须解决奇异问题.四元数法采用冗余四参数表述姿态,能够实现采用连续参数描述姿态的变化过程,并且克服了奇异问题,计算复杂度低,被广泛用于表述姿态误差,引入反馈控制[10-14].此外,四元数被广泛应用于机械手的姿态规划[15-16].

本文引入四元数法,实现机械手的姿态定向控制.通过姿态定向控制,机械手原先的六维任务(三维位置、三维姿态),转化为五维.采用姿态定向控制,可实现任务的姿态降维,从而增加机械手的冗余自由度,有效地提高机械手灵活性,有助于实现关节限位、碰撞避障、奇异点避免等约束.本文通过构建李雅普诺夫函数与姿态定向误差的表述形式,引入控制律,实现了姿态定向控制的全局稳定.实验证明,采用该方法能够有效地实现姿态定向误差收敛,计算复杂度低,便于实时控制.

1 四元数基础

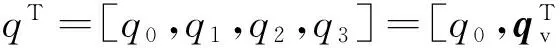
(1)

式(1)等价于

(2)

式中：四元数q表示旋转运动可以等价绕轴向K旋转角度ψ.旋转矩阵R与q的关系可以表示为

R=I3+2q0S(qv)+2S(qv)S(qv).

(3)

式中：对于任意的向量a=[a1,a2,a3]T,S(a)是对应的反对称矩阵,

(4)

将式(1)代入式 (3),可得

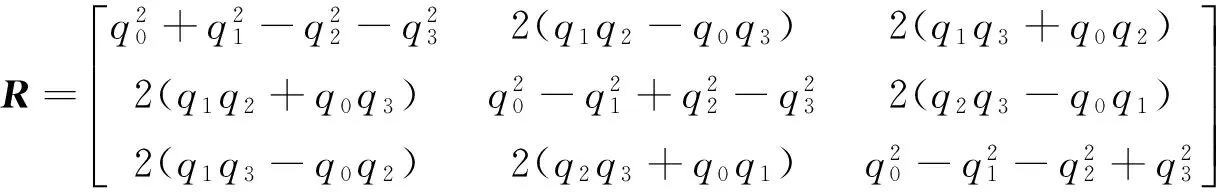
(5)

根据式(5)可知,从R中计算单位四元数q的公式如下：

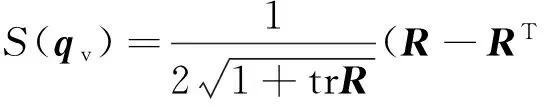
(6)

(7)

式中：E(q)为雅克比矩阵，

(8)

E(q)具有如下性质：

E(q)TE(q)=I3， E(q)Tq=0.

(9)

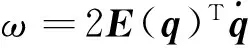
(10)

2 机械手运动控制

机械手的机械结构提供了关节空间到笛卡尔空间的映射关系：

x(t)=f(θ(t)).

(11)

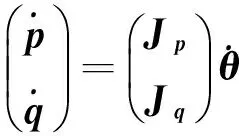
(12)

式中：p表示位置信息,q为姿态的四元数向量, Jp、Jq分别为位置与四元数的雅克比矩阵.将式(10)代入式(12),可得

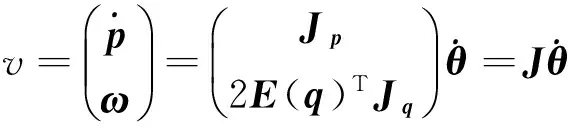
(13)

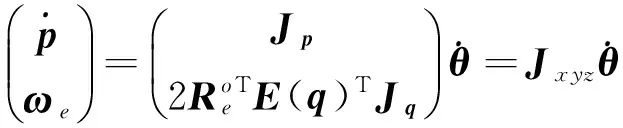
(14)

在定向控制中,绕终端坐标系下的某一轴向旋转对末端最终的执行效果无影响.通过工具坐标系的选取,可以将绕终端Z轴旋转ωez定为无效旋转,则运动学等式可以简化成

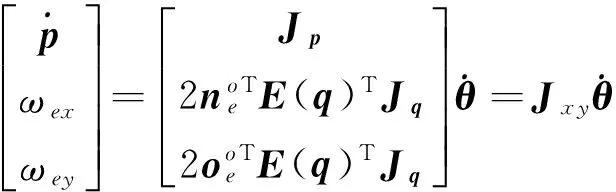
(15)

(16)

3 误差反馈与稳定性

在一般情况下,位置误差表示为p(t)-pd(t).姿态误差的表示方法根据不同的姿态表示方法,有不同的表示.对于旋转矩阵,误差形式为

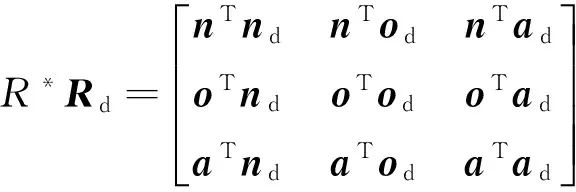
(17)

采用四元数法,姿态误差可以表示为

(18)

当末端姿态与期望姿态重合时,RdR*=I3,相对应四元数,则表示为q=qd且δq=[1,0,0,0]T.根据四元数法的几何意义可知,R*Rd与δq等价,即可以通过式(5)、(6)相互转化.对于定向问题(假设末端坐标系的Z轴为允许旋转运行的轴向),不需要使得姿态严格满足Rd=R,仅需使得a=ad,其中a为末端Z轴在基坐标系下的坐标值.

定理1 满足末端Z轴定向控制,即a=ad,只需使得δq1=0以及δq2=0.其中,δq1、δq2为式(18)中δq的分量.

证明：当a=ad时,根据式(5)、(17),可得

根据定理1可知,末端X轴定向控制须满足δq2=0及δq3=0,末端Y轴定向控制须满足δq1=0及δq3=0.

在机械手运动控制的一阶微分模型下,位置误差反馈引入ep=p-pd.假设姿态定向误差反馈引入ea=[ea1,ea2,ea3]T,其中ea为相对于末端坐标系下的姿态误差,则系统输入变量为

(19)

定义如下李雅普诺夫函数：

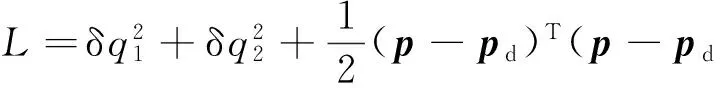
(20)

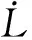
(21)式中：δq表示以末端坐标为参考坐标系,末端坐标系到期望坐标系的姿态误差.根据式(7)、(14),可知

(22)

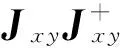
(23)

式中：å表示绕Z轴旋转运动ωez,由于采用五维度控制,该项为不可控项,其值未知.将式(23)代入式(22),可得

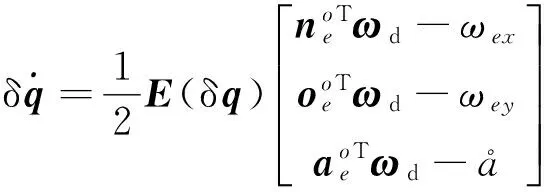
(24)

根据式(8)、(24),可得

(25)

将式(25)代入式(21),可得

(26)

(27)

4 姿态定向误差构建

在姿态定位控制中,R唯一确定,因而姿态误差的表述形式是唯一的,见式(17)、(18).在姿态定向控制中,目标任务仅需确保某一轴向的方向一致,绕其轴向的旋转运动为自由项.此时,在任务规划中,矩阵Rd无法唯一确定,从而定向姿态误差的四元数表述δq存在不确定项.

图1 姿态定向误差的通用描述示意图Fig.1 Expression of attitude pointing error

(28)

不同于姿态定位控制,在定向控制中,ψ′的动态变化对姿态定向误差没有影响.引入姿态定向误差的表述形式：

(29)

等价于忽略可能存在的轴向旋转运动项,即ψ′=0.引入式(29)作为误差反馈,根据式(27)可知,当δq1=0和δq2=0时,δq=[1,0,0,0]T.此时,定向姿态重合,误差为零.由式(29),可知

(30)

(31)

L∈[0,1].根据非线性系统的相平面分析可知,系统(31)中,除了L=1的平衡点外,其他区域都将收敛至稳定平衡点L=0.

(32)

(33)

同理,可以获取允许末端X轴向运动的姿态定向误差表述与反馈角速度：

(34)

以及允许末端Y轴向运动的姿态定向误差表述与误差反馈角速度：

(35)

5 实验结果

为了验证姿态定向控制的稳定性和提高机械手工作性能的特点,设计了2个实验：在姿态定位控制与姿态定向控制下,实现机械手击打乒乓球的任务.在实验中,7自由度机械手的DH参数α、a、d如表1所示.表中，θ为关节角.机械手运动控制采用文献[17]的钳位加权最小范数方法,基本方程为

(36)

式中：In、Im为对应关节和任务维数的单位方阵,Hw为关节逆权重对角矩阵,J为机械手雅克比,λ

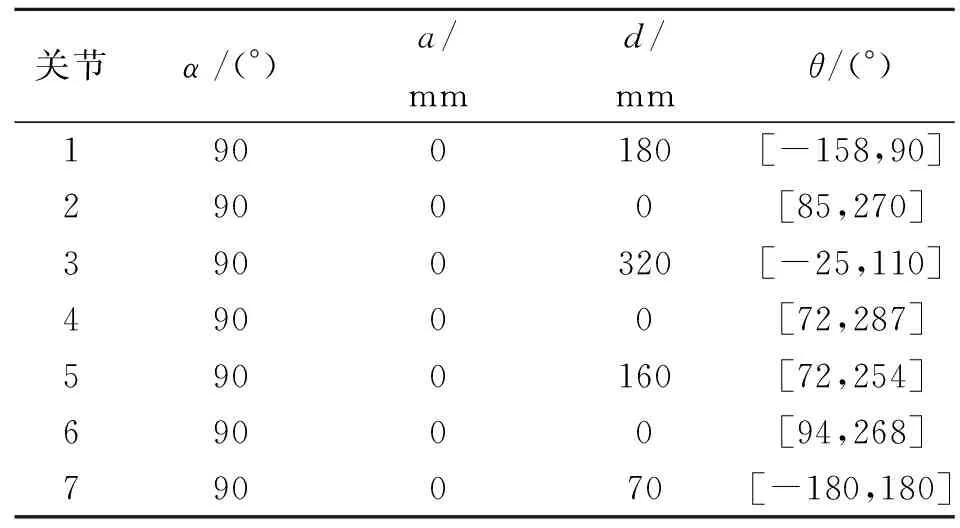
表1 乒乓球机械手DH参数

为阻尼项,φ(θ)为关节钳位项,x为机械手实际运行轨迹,xd为期望轨迹.采用该方法,机械手将在关节约束下实现位置与姿态的跟踪.在实验中,关节伺服驱动器工作在速度运行模式下,采用实时控制的方式实现关节速度指令输出.

机械手打球的某一规划任务为从初始位姿

运行至终端位姿：

运行时间为5 s.若为姿态定向控制,则终端目标的轴向任务为o=[0.500 0,0.500 0,0.707 1]T,位置与Tf相同.为了验证2种不同控制方法的误差收敛情况,设定机械手的初始关节位置为θ(0)=[-100.0,120.0,90.0,200.0,180.0,220.0,-30.0]T.在实验中,误差反馈增益设为kp=5,ka=5.

如图2、3所示为乒乓球机械手击球时采用姿态定位控制的运行结果.其中,定位控制方法参照文献[10].采用姿态定位控制方式,机械手的控制任务为六维,机械手关节数为七维,仅有一个冗余度.如图2(a)、(b)所示分别为机械手的关节运行速度与位置.图2(b)给出关节的归一化曲线.图中,θmax与θmin分别为容许的最大、最小关节位置.如图2(c)所示为机械手误差反馈后输出的控制指令,见式(19),机械手任务误差见图2(d),可知机械手的误差没有完全收敛到零.采用控制律(36),由于机械手在运行过程中,当t=3.5 s时,关节2、5、7接近于限位.为了避免关节限位约束,会引入阻尼项(λ>0),从而导致JJ+≠Im.式(23)中的条件不成立,误差全局收敛的前提条件被破坏.采用控制律(36)实现姿态定位控制,由于要保证关节限位约束,从而影响任务的执行,任务的位置与姿态跟踪误差较大,见图2(d).对于机械手,即使末端位置是可达的,末端位置与姿态也未必可达.在该实验中,末端位置与姿态未完全到位,且3个关节已接近限位,因而对应的末端位姿不一定可达.

图2 姿态定位控制下的机械手运行轨迹Fig.2 Results of attitude control using quaternion

图3 姿态定位控制运行结果Fig.3 Snaps of manipulator under attitude control

图4 姿态定向控制下的机械手运行轨迹Fig.4 Results of attitude pointing control using quaternion

如图4所示为乒乓球机械手击球时的采用姿态定向控制的运行结果.采用姿态定向控制方式,七关节的机械手的控制任务为5维,剩余2个冗余度,有利于机械手关节限位避障.由于5、7号电机负载小,低速时,在减速器、摩擦力等的影响下,速度的跟踪效果较差.如图4(d)所示为任务误差,在5、7号关节电机低速跟踪存在较大抖动的情况(见图4(a))下,采用定向姿态控制,能够良好地跟踪任务,实现位姿的误差收敛.由图4(b)可见,关节限位没有触发,机械手的权重雅克比处于良好的状态.此时,在机械手运动过程中,阻尼项λ一直为零,满足JJ+=Im,从而满足位姿收敛条件,使得任务能够良好跟踪.对比图3(a)、4(a)可以发现,采用姿态定向控制,机械手关节速度的二范数和小于姿态定位控制,机械手在消耗较少的能量下,更加精确地跟踪主任务.其中,图4(c)中的ωex、ωez与图4(d)中的ea1、ea2依赖于机械手末端当前的姿态.位置控制与姿态定位控制规划的控制指令不依赖于机械手的当前状态,定向控制的控制指令给定与误差形式都依赖于当前的机械手姿态.在采用同一控制律(36)的情况下,姿态定向控制能够更好地执行任务,有利于乒乓机械手的回球动作执行,且本身球拍面的轴向运动不影响机械手的接球任务.对应于机械手,末端的位置与姿态是否可达,转化为位置与轴向是否可达,从而扩大机械手可达区间,有利于乒乓机械手的运行及功能提升.

两种方法对应的机械手运行过程如图3、5所示.机械手末端的球拍面法线方向o分别为[0.495 5,0.502 2,0.708 7]T与[0.500 2,0.500 1,0.706 9]T.在运动过程中,球拍面轴向方向与规划方向的误差如图6所示.图中，φ为o与期望的球拍面轴向方向的夹角.对比2种方法可知,采用姿态定向控制机械手更加灵活,能够有效地避免关节限位,并且提升机械手雅克比最小奇异值,有利于关节速度的降低,从而保证伺服能够良好地跟踪速度指令.此外,采用姿态定向控制可以降低控制维度,扩大机械手姿态定向的可达区域.

图5 姿态定向控制运行结果Fig.5 Snaps of manipulator under attitude pointing control

图6 姿态定位控制和定向控制的球拍轴向误差Fig.6 Angle between axis of pingpang pat and desired direction

6 结 语

本文引入机械手的姿态定向控制方法,并且构造定向姿态误差的表述方法,实现机械手姿态定向控制的全局稳定性.通过乒乓机械手击球的实验对比,有效地证明了姿态定向控制相对于姿态定位控制的优势.一般机械手使用参数,提供机械手的空间位置运动范围,未考虑机械手在位置运动范围内的姿态范围.采用机械手实现位置和姿态控制时,如果机械手的定向姿态控制能够等效地完成相关功能,可以采用机械手姿态定向的方法,有利于机械手在关节限位约束的条件下,实现姿态和位置的良好跟踪.

[1] LUH J Y S, WALKER M W, PAUL R P C. Resolved-acceleration control of mechanical manipulators [J]. IEEE Transactions on Automatic Control, 1980, 25(3): 468-474.

[2]LIN S K. Singularity of nonlinear feedback control scheme for robots [J]. IEEE Transactions on Systems, Man and Cybernetics, 1989, 19(1): 134-139.

[3]CRASSIDIS J L, MARKIEY F L. Attitude estimation using modified Rodrigues parameters [J]. 1996: 71-83．

[4]DIMAROGONAS D V, TSIOTRAS P, KYRIAKOPOULOS K J. Laplacian cooperative attitude control of multiple rigid bodies [C]∥ IEEE International Symposium on Intelligent Control. [S. l.]: IEEE, 2006: 3064-3069.

[5]REN W. Distributed cooperative attitude synchronization and tracking for multiple rigid bodies [J]. IEEE Transactions on Control Systems Technology, 2010, 18(2): 383-392.

[6]LIN S K. Euler parameters in robot Cartesian control [C]∥ IEEE International Conference on Robotics and Automation. [S. l.]: IEEE, 1988: 1676-1681．

[7]KREUTZ K. On manipulator control by exact linearization [J]. IEEE Transactions on Automatic Control, 1989, 34(7): 763-767.

[8]CACCAVALE F, N NATALE C, SICILLIANO B, et al. Resolved-acceleration control of robot manipulators: a critical review with experiments [J]. Robotica, 1998, 16(05): 565-573．

[9]LIN S K. Singularity of nonlinear feedback control scheme for robots [J]. IEEE Transactions on Systems, Man and Cybernetics, 1989, 19(1): 134-139．[10]LIN S K. Singularity of nonlinear feedback control scheme for robots [J]. IEEE Transactions on Systems, Man and Cybernetics, 1989, 19(1): 134-139.

[11]WEN J T Y, KREUTZ-DELGADO K. The attitude control problem [J]. IEEE Transactions on Automatic Control, 1991, 36(10): 1148-1162．

[12]LIZARRALDE F, WEN J T. Attitude control without angular velocity measurement: a passivity approach [J]. IEEE Transactions on Automatic Control, 1996, 41(3): 468-472．

[13]CACCAVALE F, SICILLIANO B. Quaternion-based kinematic control of redundant spacecraft/manipulator systems [C]∥ IEEE International Conference on Robotics and Automation. [S. l.]: IEEE, 2001: 435-440.

[14]XIAN B, DE UEIROZ M S, DAWSON D, et al. Task-space tracking control of robot manipulators via quaternion feedback [J]. IEEE Transactions on Robotics and Automation, 2004, 20(1): 160-167.

[15]TAYLOR R H. Planning and execution of straight line manipulator trajectories [J]. IBM Journal of Research and Development, 1979, 23(4): 424-436．

[16]刘松国, 朱世强, 王宣银, 等. 基于四元数和 B 样条的机械手平滑姿态规划器[J]. 浙江大学学报: 工学版, 2009, 43(7): 1192-1196. LIU Song-guo, ZHU Shi-qiang, WANG Xuan-yin,et al．Smooth orientation planner for manipulators based on quaternion and B-spline [J]. Journal of Zhejiang University: Engineering Science, 2009, 43(7): 1192-1196．

[17]HUANG S, PENG Y, WEI W, et al. Clamping weighted least-norm method for the manipulator kinematic control: avoiding joint limits [C]∥Control Conference (CCC). [S. l.]: IEEE, 2014: 8309-8314.

Attitude pointing control of manipulator based on quaternion

HUANG Shui-hua, JIANG Pei,WEI Wei, XIANG Ji, PENG Yong-gang

(CollegeofElectricalEngineering,ZhejiangUniversity,Hangzhou310027,China)

A general framework for the kinematic control of manipulator with attitude pointing task was presented. Attitude pointing task is keeping the direction of end-effector instead of its attitude following the command. The nonsingular unit quaternion was adopted in the manipulator kinematic control. The expression of attitude pointing error using quaternion was introduced, and Lyapunov function was constructed to prove the global stability of proposed method used in the closed-loop inverse kinematic control. By using attitude pointing control, the manipulator would get an extra degree of freedom compared to the attitude control. The manipulator would have better dexterity and manipulability. The ability of avoiding joint limits and obstacles was improved. The experiments implemented on a 7-DOF manipulator verified the theoretical results and good performance of attitude pointing control. The comparison with attitude control was given to show the advantages of proposed method．

attitude pointing; attitude control; quaternion; robot kinematic

2015-05-18. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

国家自然科学基金资助项目(61374174)；浙江省自然科学基金资助项目(LY13F030001)；杭州市重大科技创新产业链资助项目(20132111A04).

黄水华(1990-),男,博士生,从事机械手运动控制、视觉伺服研究.ORCID: 0000-0001-6928-6404. E-mail: eehuangsh@gmail.com 通信联系人：韦巍,男,教授,博导. ORCID: 0000-0002-7021-2792. E-mail: wwei@zju.edu.cn

10.3785/j.issn.1008-973X.2016.01.025

TP 241

A

1008-973X(2016)01-0173-07