轮印载荷下多跨梁最危险工况分析与优化

康杰豪，贺远松，谭开忍，贺梦豪，刘均，程远胜

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2中国船舶及海洋工程设计研究院，上海200011

轮印载荷下多跨梁最危险工况分析与优化

康杰豪1，贺远松2，谭开忍2，贺梦豪1，刘均1，程远胜1

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2中国船舶及海洋工程设计研究院，上海200011

多种轮印载荷工况作用于船舶多跨梁结构时，找到最危险工况并进行结构优化设计，对于船舶结构的安全校核与降低结构重量有重要意义。提出一种将遗传算法与有限元方法相结合，以多跨梁上轮印载荷的布置位置为设计变量，载荷间的间距大小为约束条件，每一跨的最大弯矩和最大剪力为目标函数，求解任意多跨梁上有多种轮印载荷作用时最危险工况的方法，并根据最危险工况分析的结果调整支座位置，降低多跨梁最大弯矩，并进一步进行构件尺寸的优化设计。计算结果表明：基于提出的多跨梁优化设计方法，能找到每一跨应力满足强度要求的剖面积最小的构件尺寸，且构件尺寸的变化对最危险工况时的最大弯矩与轮印载荷位置几乎没有影响。调整支座位置的优化方案，与支座初始位置方案相比，最危险工况时的最大弯矩降低22.64%，重量降低10.55%，因此支座位置的调整，能有效降低最危险工况时的最大弯矩，从而达到降低多跨梁重量的目的。

轮印载荷；多跨梁；最危险工况分析；优化设计；遗传算法

0 引 言

滚装船上的运货车辆以及现代舰艇上的直升机等都是通过轮印载荷作用于装载甲板的，轮印载荷具有局部重载与位置不确定的特点。多跨梁结构是船舶上常见的一种结构形式，船舶上的强横梁、纵桁等主要构件，都可以看作是一种多跨梁结构。因此，在多种轮印载荷工况中，找到多跨梁的最危险工况，并对其进行结构优化设计，对于船舶结构的安全校核与降低结构重量具有重要的意义。

多工况分析在船舶设计领域已经得到广泛的应用。毛鲁杰［1］研究了不同装载工况、不同浪向角和不同波浪频率对6 900车汽车运输船的波浪诱导载荷的影响，并对其进行了预报。刘英良［2］对超大型集装箱船多工况点的最佳方形系数范围进行了探索，提出了具有参考价值和推广意义的多工况技术指标拆解方法和分析流程。朱明华［3］研究了多工况集装箱船的配载与堆场翻箱的优化，建立了相关问题的数学模型，并设计了启发式算法进行求解。遗传算法在船舶优化设计中也有广泛的应用［4］。权义柯［5］用遗传算法对滚装船车辆配载进行了优化，其结果优于传统配载方法。Zakerdoost等［6］在减少阻力的船型优化设计中运用了遗传算法。近年来，国内外都有研究学者把遗传算法与危险工况分析结合，运用遗传算法进行危险工况分析。吕谋等［7］基于遗传算法对给水管网进行了多工况分析与优化设计，并验证了该方法的实用性。万文等［8］运用加速混合遗传算法搜索边坡最危险滑动面。Forouraghi［9］通过遗传算法寻找公差设计与质量保证时的最危险工况。Jeons等［10］分析了遗传分析方法应用于最危险工况分析的算法性能，并成功找到了数个经典数学问题的最危险工况。方陆鹏等［11］将轮印载荷简化为集中力，制作了轮印载荷下连续多跨梁结构模型的试验装置，并对比了弯矩的理论值与实验值，结果基本一致，但对于轮印载荷下船舶多跨梁结构的最危险工况分析与优化设计还缺乏深入研究。

本文基于安全的考虑，将船舶多跨梁装载工况中的轮印载荷简化为集中力，将遗传算法和有限元方法相结合，对多跨梁进行最危险工况分析，获得多跨梁中每一跨弯矩、剪力最大时分别对应的轮印载荷位置；并根据求得的多跨梁最危险工况，对多跨梁的构件尺寸和支座位置进行优化。

1 轮印载荷下多跨梁最危险工况分析

船舶装载甲板上车辆的数目虽然固定，但位置可能随着调动而改变，对应的轮印载荷布置工况也有多种，因此难以直接判断出船舶上多跨梁发生最大内力时所对应的最危险工况。轮印载荷下的多跨梁最危险工况分析即是指当一个多跨梁的几何参数已定，轮印载荷有多种布置工况时，通过优化的方式，借助遗传算法，获得多跨梁上每一跨的最大弯矩和最大剪力的值，以及其对应的载荷工况。

1.1 几何模型

图1为1个n跨不等刚度和不等间距的多跨梁，总长为L。第i跨梁的长度为li，弹性模量为Ei，泊松比为vi，构件型号为Ti。一共m组轮印载荷作用于多跨梁上，第j组轮印载荷中轮印载荷的个数为sj；Fj，k表征轮印载荷的集中力，表示对应第j组轮印载荷中的第k个轮印载荷；xj表示第j组载荷中的首载荷与多跨梁左端的间距；Dj，k表示第j组载荷第k个轮印载荷与第k+1个轮印载荷的间距。

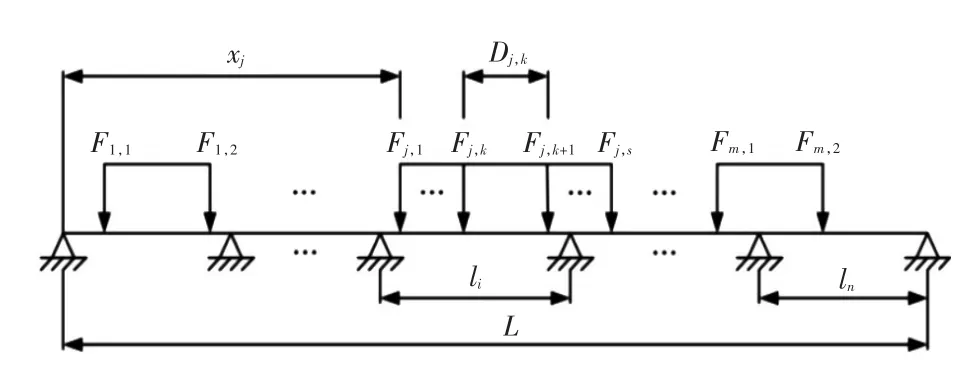
图1 多跨梁几何模型及其轮印载荷示意图Fig.1 The geometric model of multi-span beams under patch loading condition

1.2 数学模型

1.2.1 设计变量

多跨梁最危险工况分析的变量为轮印载荷的布置工况，对应上述几何模型，当一组轮印载荷中首载荷的位置已定时，该组轮印载荷的布置也固定，因此用每组轮印载荷中的首载荷与多跨梁左端的间距xj作为设计变量。

1.2.2 目标函数

多跨梁最危险工况分析的目标函数为多跨梁上每一跨的最大弯矩Mi或最大剪力FSi。本文多跨梁内力分析采用有限元分析软件ANSYS建立有限元模型计算获得，建模时选用3D梁单元BEAM 188模拟梁结构，每跨梁的网格份数为20。

为了验证有限元模型的正确性，采用上述建模方式计算文献［11］中多跨梁模型的弯矩，并与其给出的理论值对比，弯矩图如图2所示。

从图2可以看出，本文采用的有限元建模方法计算的多跨梁弯矩值与理论值几乎完全一致，证明有限元数值计算结果有足够的精度。

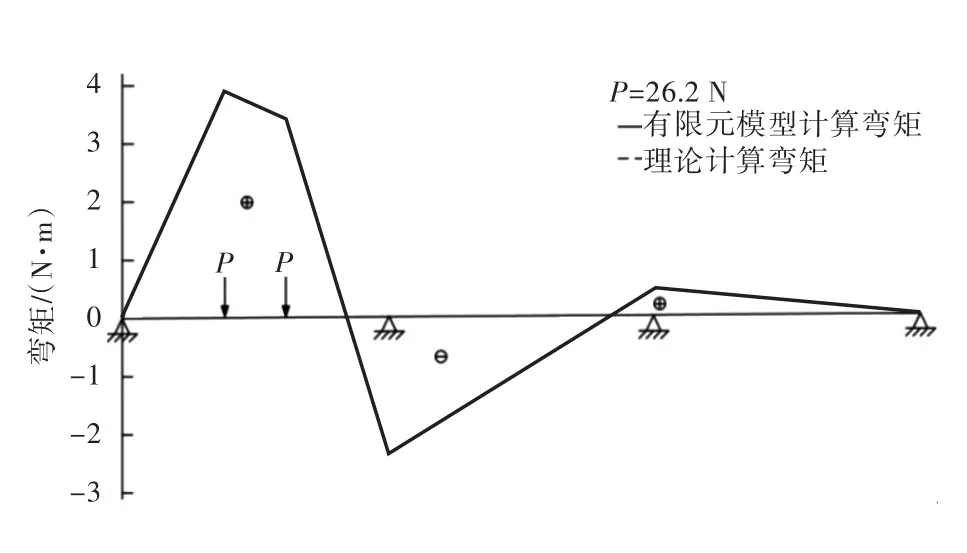
图2 某多跨梁模型弯矩图Fig.2 Bending moment diagram of a multi-span beam

1.2.3 约束条件

在实际装载情况中，船舶装载甲板上相邻车辆的间距需满足一定的要求，因此多跨梁最危险工况分析的约束条件为相邻2组轮印载荷的间距大小。

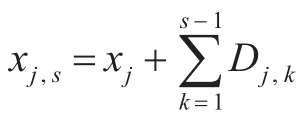
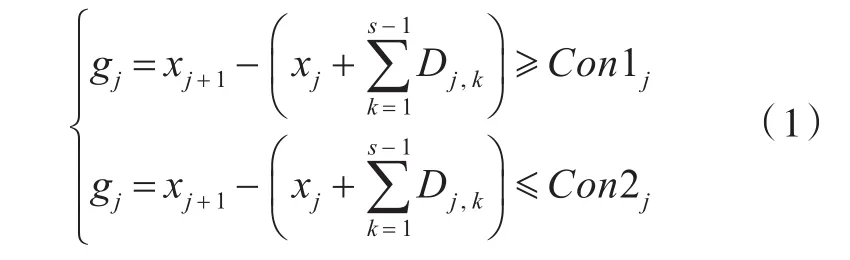
式中：Con1j和Con2j分别表示第j组载荷与第j+1组载荷之间需要满足的最小间距与最大间距。

由于遗传算法在执行交叉、变异操作时存在随机性，所产生的新个体中必然会存在一些不符合约束条件的个体，惩罚函数法［4］对不满足约束条件的个体，计算其适应度时，处以一个惩罚函数，从而降低该个体的适应度，使该个体被遗传到下一代群体中的机会较少。因此本文采用惩罚函数法处理上述最危险工况分析的约束条件，设计了如下的惩罚因子C：

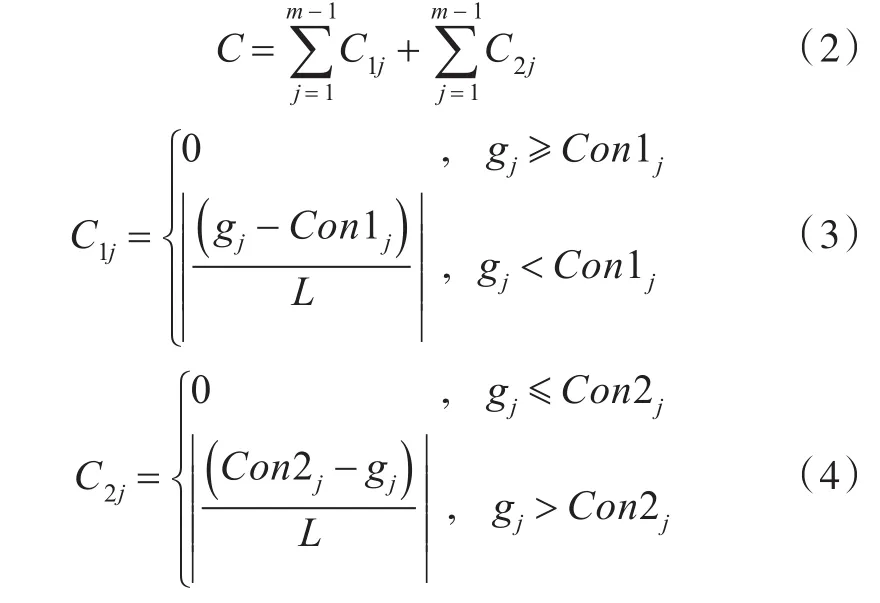
每一跨最大弯矩的目标函数Mi和最大剪力的目标函数FSi可分别表示为：

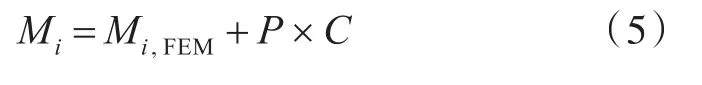
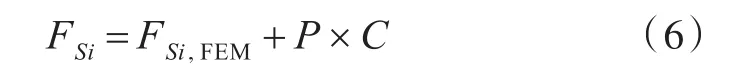
式中：Mi，FEM和 FSi，FEM分别表示第i跨最大弯矩和第i跨最大剪力；P为惩罚因子的放大系数；C为惩罚因子。

1.3 分析步骤与流程

轮印载荷下多跨梁最危险工况分析的流程如图3所示，分为以下4个步骤：

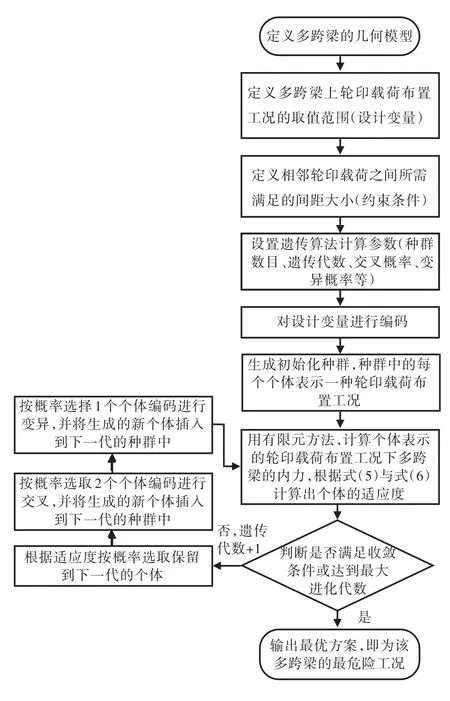
图3 轮印载荷下多跨梁最危险工况分析流程图Fig.3 Flow chart of the worst-case analysis of multi-span beams under patch loading

1）定义多跨梁的几何模型，即输入多跨梁的材料、尺寸参数。

2）定义设计变量与约束条件，即设置轮印载荷布置工况的取值范围，以及相邻轮印载荷之间所需满足的间距大小。

3）设置遗传算法参数（种群数目、遗传代数、交叉概率和变异概率等），参数值根据具体问题设计空间的大小，必要时可以反复试算找到合适值。

4）在数学软件Matlab中通过调用ANSYS计算多跨梁弯矩和剪力，采用遗传算法计算出每一跨的最大弯矩目标函数Mi，以及最大剪力目标函数FSi及其对应的载荷工况并输出结果。

2 多跨梁构件尺寸优化设计

多跨梁构件尺寸优化是指当多跨梁上每一跨的最大弯矩Mi和最大剪力FSi已知时，根据多跨梁的许用正应力σ和许用剪应力τ，采用枚举法在型材库中找到满足约束条件时剖面积最小的构件尺寸，以此达到降低多跨梁结构重量的目的。

2.1 数学模型

2.1.1 设计变量

设计变量为多跨梁的构件尺寸。具体构件尺寸的取值范围如表1所示。

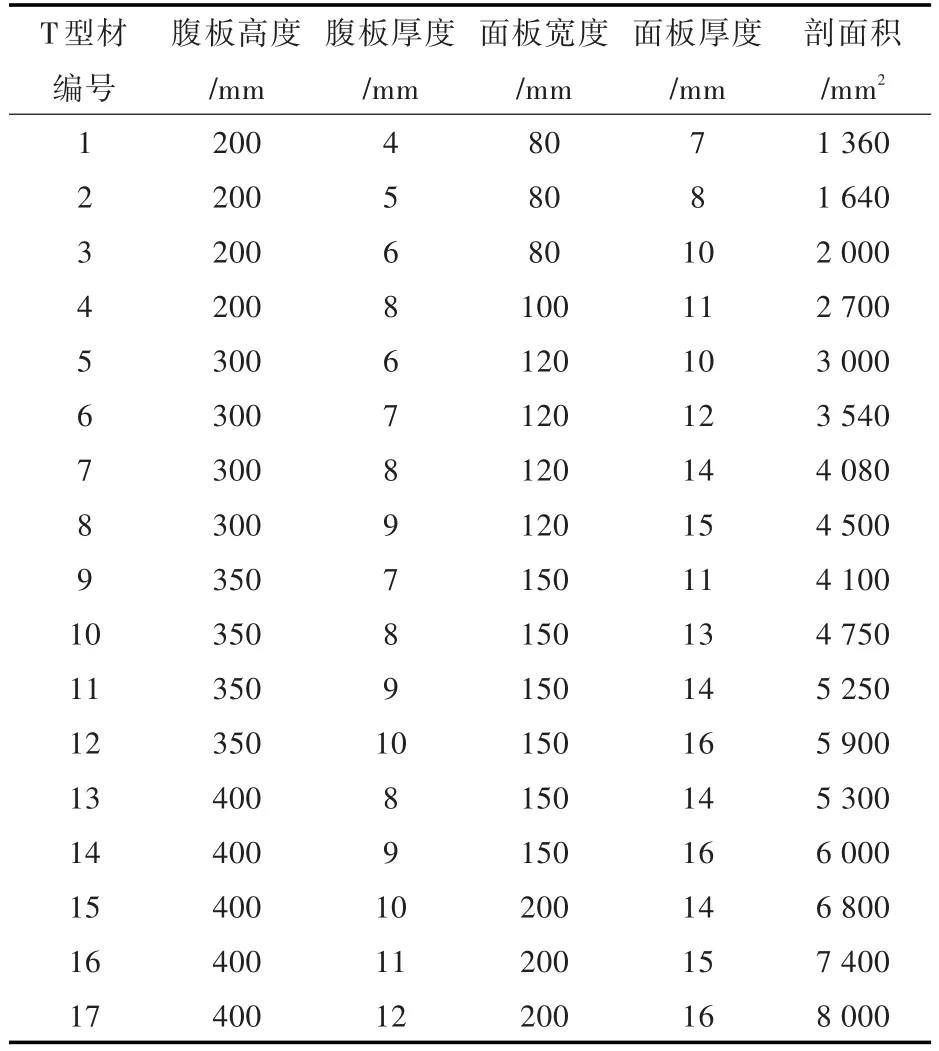
表1 多跨梁的构件尺寸优化设计型材库Tab.1 Scantling range of the multi-span beams

2.1.2 目标函数

目标函数为多跨梁结构的重量。

2.1.3 约束条件

已知多跨梁的许用正应力σ和许用剪应力τ，多跨梁构件尺寸优化设计应满足以下约束条件［12］：

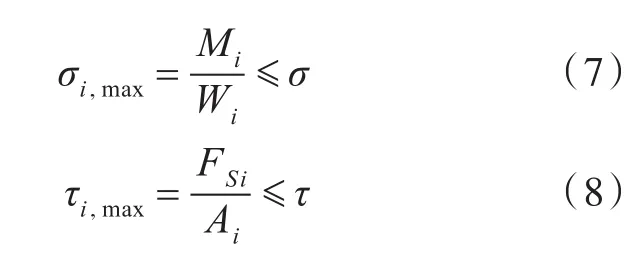
式中：σi，max为第i跨梁的最大正应力；Wi为第i跨梁的抗弯剖面模数；τi，max为第i跨梁的最大剪应力；Ai为第i跨梁的等效剪切面积。

2.2 优化步骤

1）定义多跨梁的几何模型，即输入多跨梁的材料和尺寸参数。

2）定义设计变量，即生成型材库作为构件尺寸的取值范围。

3）通过枚举法，在型材库中找到每一跨满足约束条件式（7）与式（8）时剖面积最小的构件尺寸，并输出每一跨的构件尺寸与多跨梁结构的重量。

3 基于最危险工况分析的多跨梁优化设计

分析多跨梁最危险工况的结果，可以作为多跨梁构件尺寸优化设计的输入；而多跨梁构件尺寸优化设计的结果，也可以作为多跨梁最危险工况分析的输入。若反复上述迭代直至多跨梁的构件尺寸不再变化，则可以认为该迭代达到收敛。

基于最危险工况分析的多跨梁优化设计是本文提出的一种基于上述迭代过程，对多跨梁的支座位置与构件尺寸同时进行优化的设计方法。通过对初始多跨梁的最危险工况分析，比较每一跨的最大弯矩Mi和最大剪力FSi，对多跨梁的支座位置提出调整方案，使得多跨梁整体的最大弯矩M或最大剪力FS得到降低。并通过多跨梁最危险工况分析与多跨梁构件尺寸优化设计的迭代，找到每个支座位置对应的多跨梁最优构件尺寸与最轻重量。最后比较多个支座位置的多跨梁方案，找到多跨梁最大弯矩M和最大剪力FS最小的方案，或者结构重量最轻的方案。

基于最危险工况分析的多跨梁优化设计的流程如图4所示，分为以下6个步骤：

1）定义初始多跨梁。

2）对初始多跨梁进行最危险工况分析（具体步骤见1.3节）。

3）根据最危险工况分析得到的每一跨最大弯矩和最大剪力，提出多跨梁支座位置的调整方案，设初始支座方案编号n=1，总共有N个支座方案。

4）对第n个支座方案进行最危险工况分析，并根据最危险工况分析的结果进行构件尺寸优化设计（具体步骤见2.2节）。

5）判断优化后的构件尺寸是否改变。若是，则将新的构件尺寸代入原多跨梁，返回第4步继续计算；若否，则表示迭代收敛，保存当前结果为第n个支座方案的计算结果。

6）判断N是否大于n。若是，则n=n+1，返回第4步继续计算；若否，则比较N个支座方案的目标函数（最大弯矩M，最大剪力FS或结构总重量），输出最优的支座方案，计算完毕。

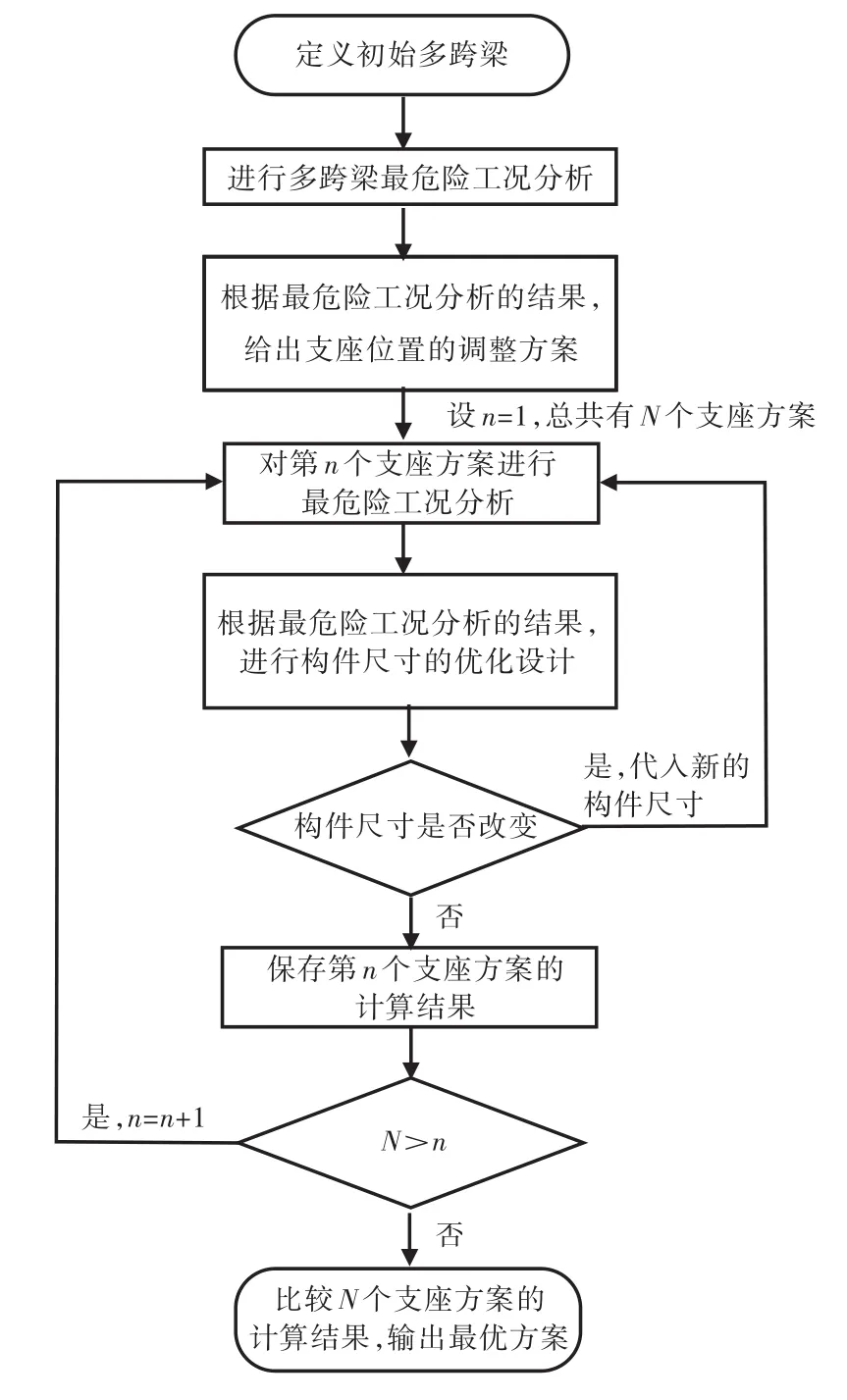
图4 基于最危险工况分析的多跨梁优化设计流程图Fig.4 Flow chart of optimization design of multi-span beams based on the worst-case analysis

4 计算实例

4.1 多跨梁最危险工况分析的计算实例

本文多跨梁最危险工况分析计算实例考虑了4种总长L皆为30 m的不同方案：方案1为每跨长15 m的两跨梁；方案2为每跨长10 m的三跨梁；方案3为每跨长7.5 m的四跨梁；方案4为每跨长15 m的两跨梁。除跨长与跨数不同之外，4种方案的其他参数都相同，但方案4只受到前2组轮印载荷作用，如图5所示。

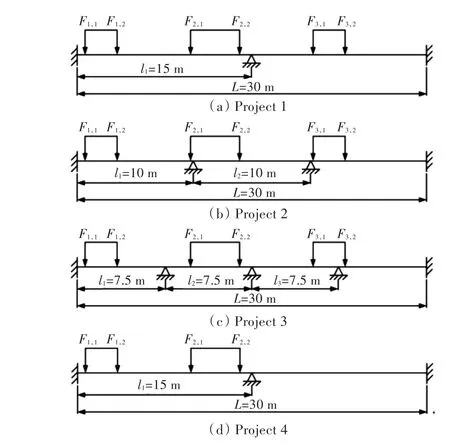
图5 多跨梁最危险工况计算实例示意图Fig.5 Example of the worst-caseanalysis of multi-span beams

多跨梁的两端刚性固定，受到3组轮印载荷作用。多跨梁材料的弹性模量E=210 GPa，泊松比v=0.3，密度 ρ=7 800 kg/m3。每组轮印载荷皆可简化为2个集中力，其中集中力的大小F1，1=80 kN，F1，2=120 kN，F2，1=60 kN，F2，2= 60 kN，F3，1=120 kN，F3，2=80 kN；每组载荷的集中力之间的距离 D1，1=4 m ，D2，1=6 m ，D3，1=4 m。多跨梁的梁截面为T型材，与其相连的带板每一跨的尺寸参数皆相同，带板宽度1 000 mm，带板厚度15 mm，T型材取表1中T型材编号13（腹板高度400 mm，腹板厚度8 mm，面板宽度150 mm，面板厚度14 mm）。

设计变量xj取值范围如表2所示。约束条件为相邻2组轮印载荷之间的最小间距不小于1 m，最大间距不大于5 m。

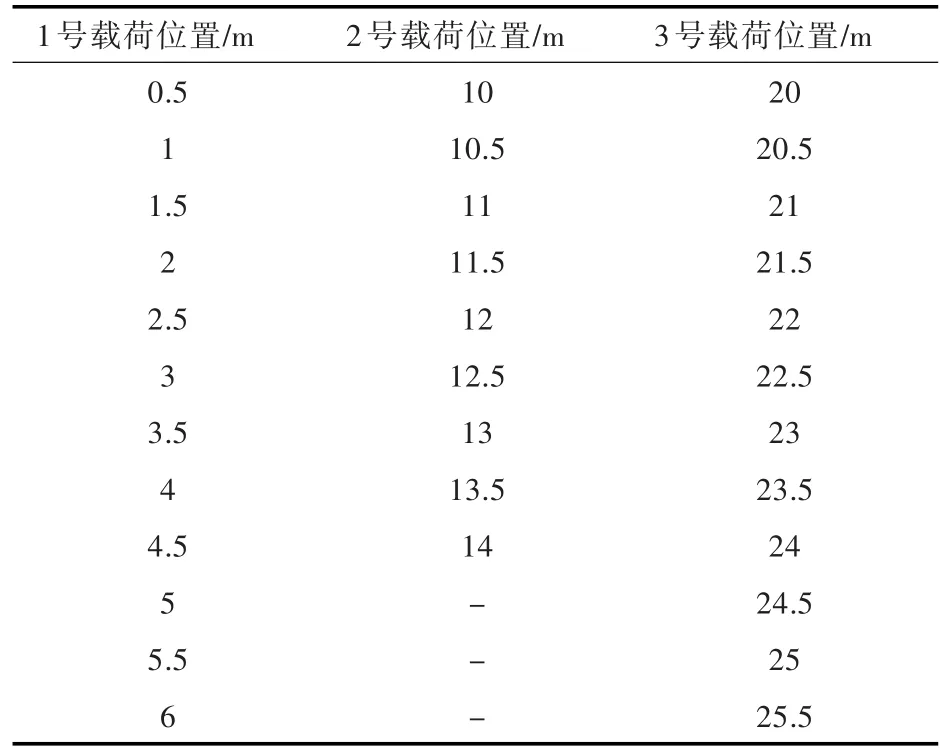
表2 多跨梁最危险工况分析的设计变量取值范围Tab.2 Design variable range of the worst-case analysis of multi-span beams

遗传算法的参数取值为种群个数50个，最大遗传代数20代，且连续10代最优解相同时终止计算，交叉概率0.85，变异概率0.1。图6为方案1中第1跨最大弯矩的遗传算法计算结果，从图中可看出因为连续10代最优解相同，计算在第17代判断收敛。最终多跨梁最危险工况分析的计算结果如表3所示。

从表3可以看出，因为上述前3个计算实例在设定时是对称的，因此计算结果中对称的梁所对

应的最危险工况的最大弯矩和最大剪力是相同的；对称的梁所对应的最危险工况的轮印载荷位置也是对称的。

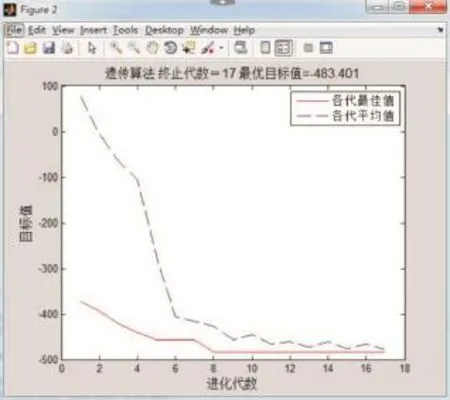
图6 方案1第1跨最大弯矩的遗传算法计算结果Fig.6 The maximum bending moment of the first span in project 1 by using genetic algorithm

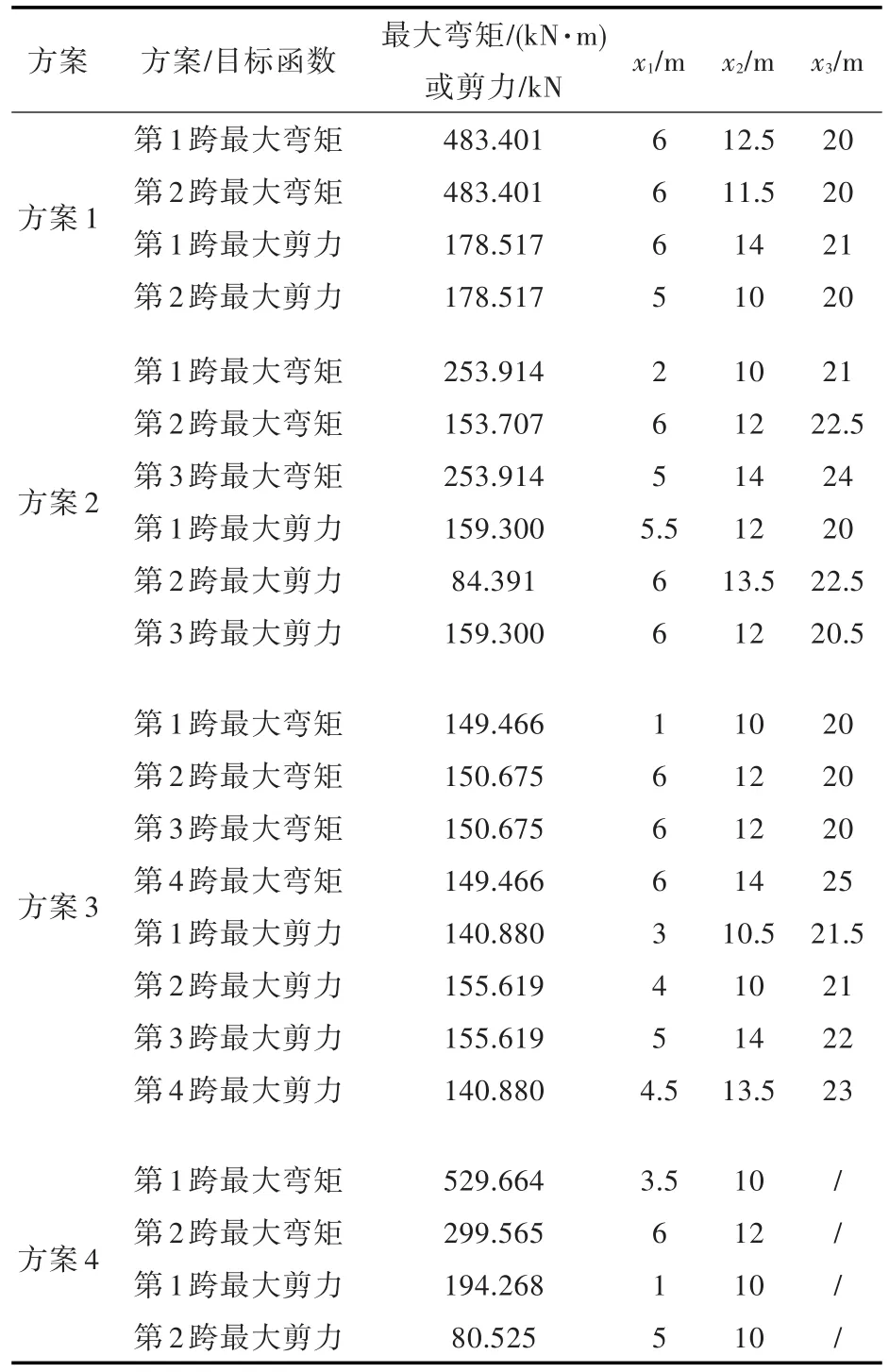
表3 多跨梁最危险工况分析的计算结果Tab.3 Numerical results of the worst-case analysis of multi-span beams

方案2中，第1跨和第3跨的最大弯矩比第2跨大65.19%，第1跨和第3跨的最大剪力比第2跨大88.76%。方案4中，第1跨的最大弯矩比第2跨大76.81%，第1跨的最大剪力比第2跨大141.25%。由此可看出，因为多跨梁的每一跨使用的构件尺寸相同，所以方案2的第2跨与方案4的第2跨的弯矩与剪力会有较大的富裕，这也说明其构件尺寸有较大的优化空间。

4.2 多跨梁构件尺寸优化设计的计算实例

根据4.1节中多跨梁最危险工况分析的计算结果，本文以4.1节的4个方案作为初始方案进行构件尺寸的优化设计。多跨梁的许用正应力σ= 355 MPa，许用剪应力τ=248.5 MPa。构件尺寸的取值范围如表1所示。初始方案及构件尺寸优化方案的计算结果如表4所示。

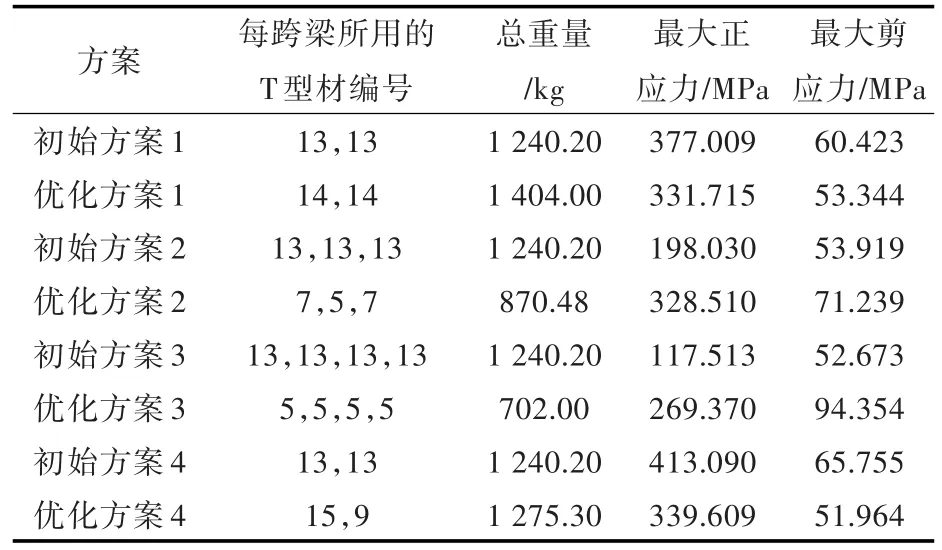
表4 多跨梁初始方案及构件尺寸优化的计算结果Tab.4 The numerical results of the original scheme and scantling optimization of multi-span beams

从表4可以看出，4个方案的剪应力相比正应力都有很大的余量，因此每一跨的最大弯矩是此时控制多跨梁构件尺寸的主要因素。优化方案1与初始方案1对比，总重量增大了13.21%，优化方案4与初始方案4对比，总重量增大了2.83%，之所以出现优化后方案的总重量大于初始方案的原因，在于初始方案1与初始方案4的最大正应力分别为377.009与413.090 MPa，比多跨梁的许用正应力大，因此初始方案的构件尺寸并不满足优化的约束条件。优化方案2与初始方案2对比，总重量减小了29.81%。优化方案3与初始方案3对比，总重量减小了43.40%。

4.3 基于最危险工况分析的多跨梁优化设计的计算实例

本文以4.1节的4个方案作为初始方案，进行基于最危险工况分析的多跨梁优化设计。多跨梁材料的许用正应力σ=355 MPa，许用剪应力τ= 248.5 MPa。

根据4.1节中最危险工况分析的计算结果，可以看出方案1与方案3中每一跨的最大弯矩几乎相同，因此无需进行支座位置的优化设计。方案

2中第1跨与第3跨的最大弯矩比第2跨大65.19%，因此本文对方案2支座位置的调整策略是减小第1跨与第3跨的跨距，增大第2跨的跨距。方案4中第1跨的最大弯矩比第2跨大76.81%，因此本文对方案4支座位置的调整策略是减小第1跨的跨距，增大第2跨的跨距。具体优化设计的支座位置取值如表5所示。每种方案优化后的目标函数值如表6所示。

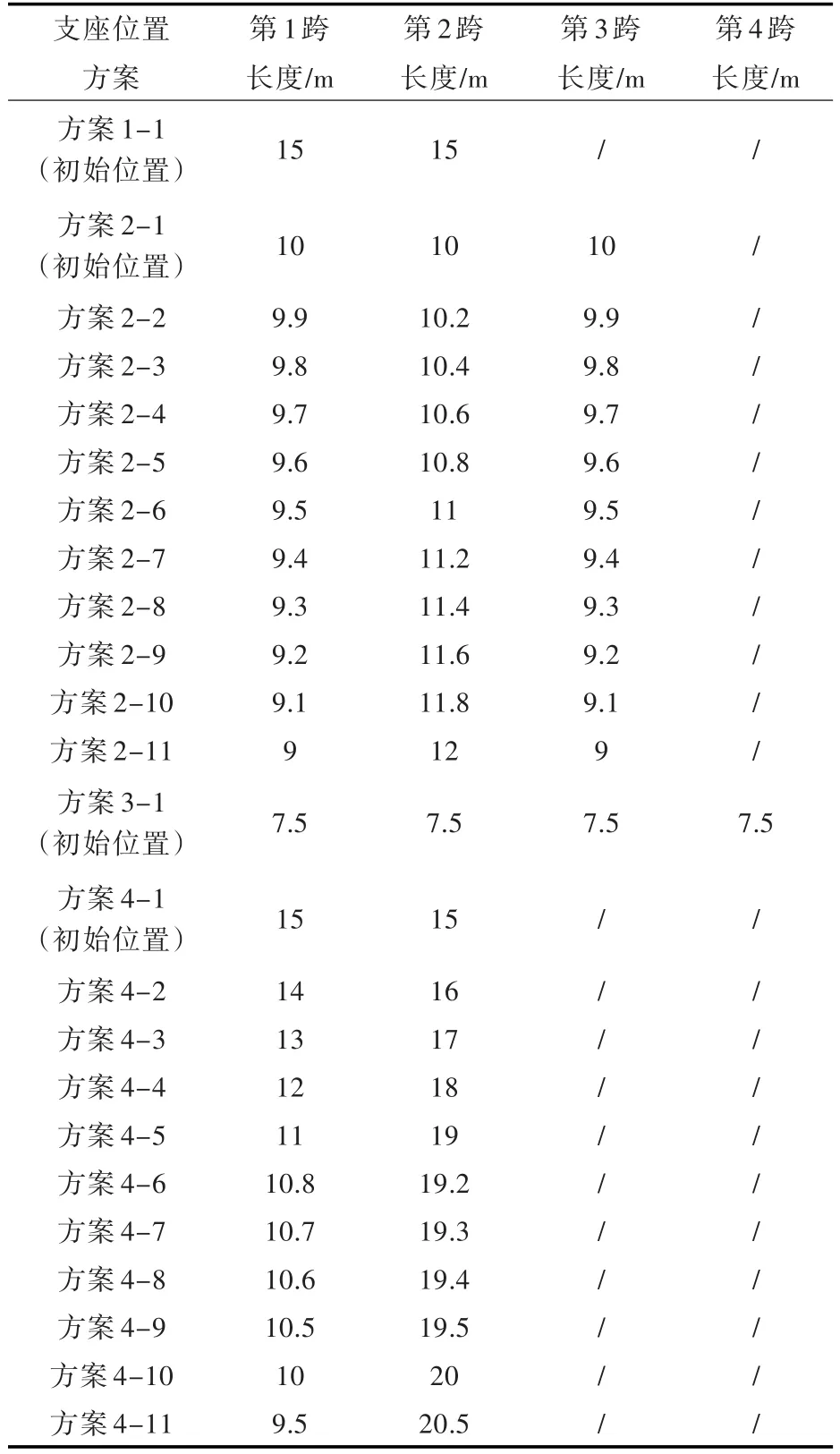
表5 多跨梁优化设计的支座位置取值方案Tab.5 Support position scheme for multi-span beams optimization design

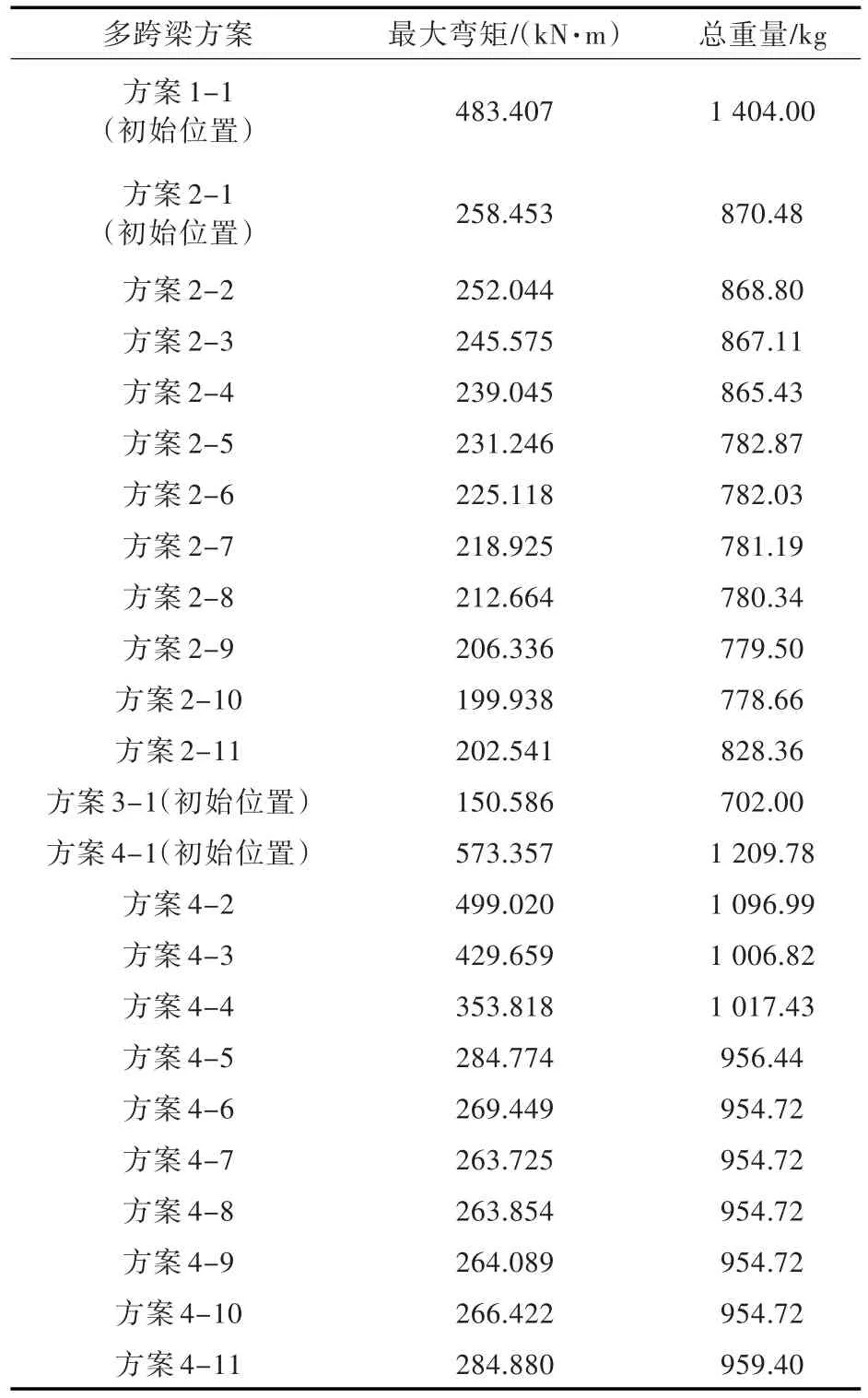
表6 支座方案优化后的目标函数值Tab.6 Target function value of optimizing design of the support position scheme in Tab.4

由目标函数值对比可以看出，方案2的各种支座位置中，方案2-10的目标函数是最优的，因此方案2-10为方案2中最优的支座位置。方案4的各种支座位置中，方案4-3的最大弯矩值比方案4-4要大，但是其总重量比方案4-4要小，说明在支座调整过程中，随着第1跨的最大弯矩减小，第2跨的最大弯矩在增大，总重量因此不是单调递减的。方案4-6，4-7，4-8，4-9与4-10的总重量相同，但因为方案4-7的最大弯矩值最小，因此方案4-7为方案4中最优的支座位置。多跨梁优化设计最优解的详细计算结果如表7和表8所示。

从表6可看出，方案2-10的最大弯矩比方案1-1的最大弯矩减小了58.64%；方案3-1的最大弯矩比方案2-10的最大弯矩减小了24.68%。方案2-10的总重量比方案1-1的总重量减小了44.54%；方案3-1的总重量比方案2-10的总重量减小了9.85%。支座数目的增加会使多跨梁的重量下降，但同时也增加了船舶支撑构件的重量，因此对于船舶结构总重量的改变需要结合实际船舶结构进行分析。

从表3与表6可看出，优化方案1-1与初始方案1对比，最大弯矩增大了0.001 2%，优化方案2-1与初始方案2对比，最大弯矩增大了1.79%，优化方案2-10与初始方案2对比，最大弯矩减小了21.26%，优化方案2-10与优化方案2-1对比，最大弯矩减小了22.64%，优化方案3-1与初始方案3对比，最大弯矩减小了0.059%，优化方案4-1与初始方案4对比，最大弯矩增大了8.25%，优化方案4-7与初始方案4对比，最大弯矩减小了50.21%，优化方案4-7与优化方案4-1对比，最大

弯矩减小了54.00%。支座位置不变时，构件尺寸优化对最大弯矩的影响不大，且对应的轮印载荷位置不变。

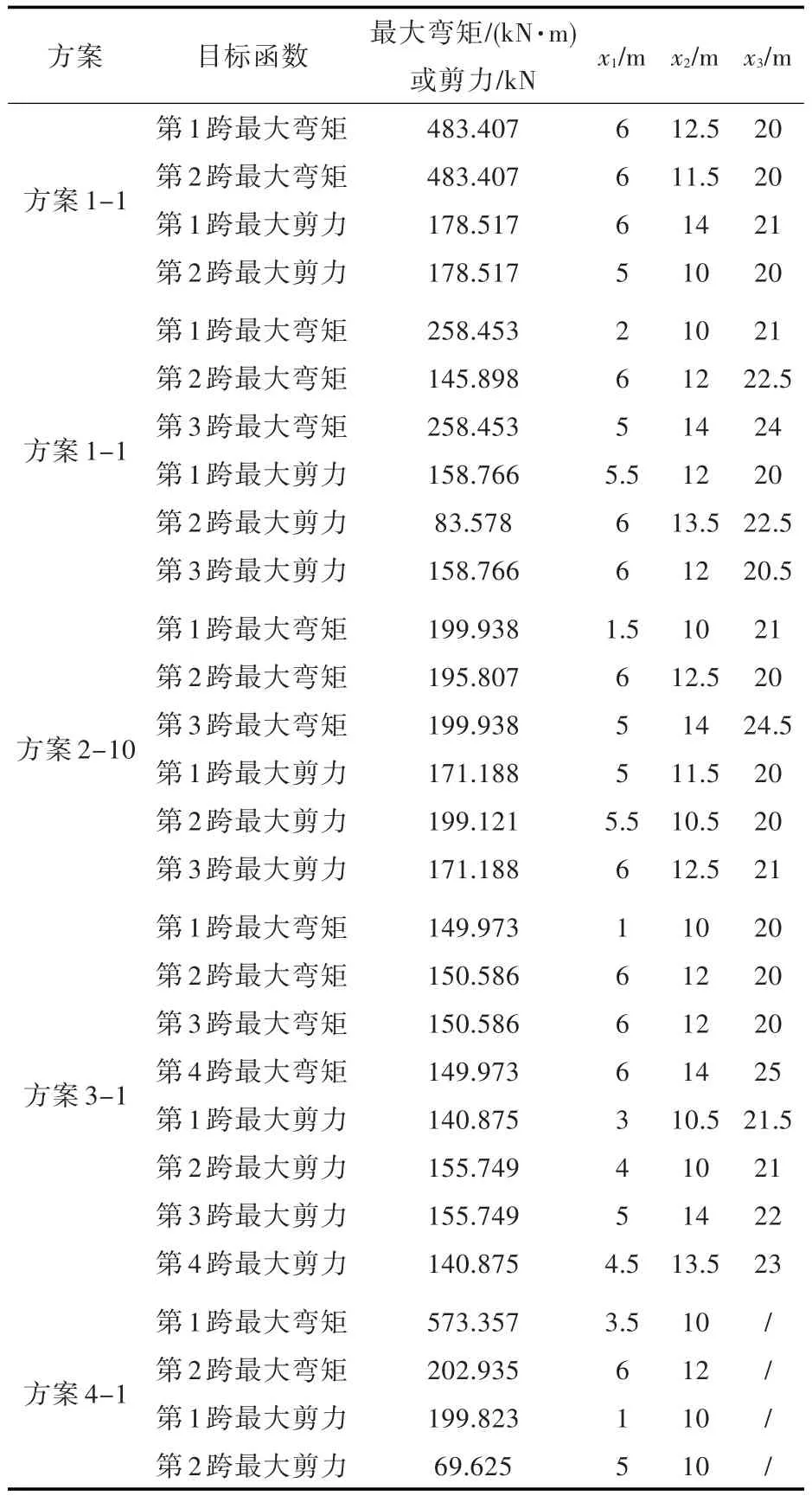
表7 多跨梁优化设计最优解的每跨最危险工况Tab.7 The worst-case analysis result of optimum solution of multi-span beams optimization design

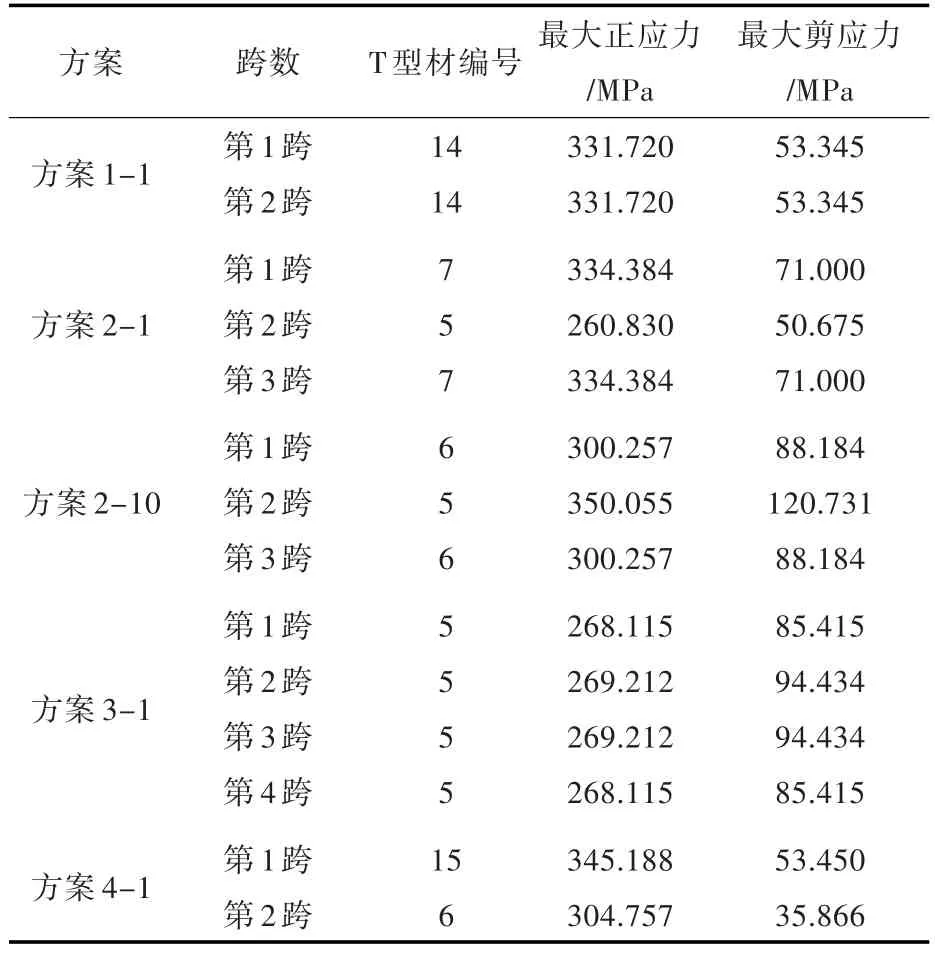
表8 多跨梁优化设计最优解的每跨最优构件尺寸Tab.8 The best scantling of optimum solution of multi-span beams optimization design

从表4与表8可看出前3种方案中初始支座位置的3个优化方案与4.2中的优化方案构件尺寸一致，因此对于重量改变也相同。从表4和表6可以看出，优化方案2-10与初始方案2相比，总重量减小了37.21%。优化方案2-10与优化方案2-1对比，总重量减小了10.55%。方案4中初始支座位置的优化方案4-1经过迭代后与4.2中的优化方案有所不同，总重量比初始方案4减小了2.45%。优化方案4-7与初始方案4对比，总重量减小了23.19%，优化方案4-7与优化方案4-1对比，总重量减小了21.08%。

5 结 论

本文将船舶多跨梁装载工况中的轮印载荷简化为集中力，将遗传算法和有限元方法相结合，提出了多跨梁最危险工况分析与优化设计的方法，并对参数相同的两跨梁、三跨梁和四跨梁计算实例进行了最危险工况分析与优化设计，主要结论如下：

1）提出多跨梁最危险工况分析方法，可以计算出多跨梁上每一跨梁的最大弯矩与最大剪力，并找出最大弯矩与最大剪力所对应的载荷位置，具有通用性。还可进一步调整支座位置来降低多跨梁的最大弯矩。根据多跨梁每一跨的最大弯矩，可以获得多跨梁每一跨所需的构件尺寸。

2）构件尺寸优化能够有效降低多跨梁的总重量，但对于多跨梁的最大弯矩影响不大，且最大弯矩对应的轮印载荷位置没有改变；多跨梁支座位置的优化，可以降低多跨梁的最大弯矩。

3）跨数不同但其他参数相同的多跨梁经过优化设计后，多跨梁的最大弯矩与总重量都随着跨数增加而降低，但降低的幅度随着跨数增加而逐渐减小。在实际船舶结构设计中，跨数增加同时也增加了船舶支撑构件的重量，所以跨数改变对于船舶结构总重量的影响还需要结合实际船舶结构具体分析。

［1］ 毛鲁杰.6900车汽车运输船疲劳强度评估［D］.舟山：浙江海洋学院，2014.

［2］ 刘英良.超大型集装箱船多工况点的最佳方形系数范围探索［J］.船舶，2014（1）：21-24. LIU Yingliang.On optimized block coefficient range

for ultra large container vessels under multiple operating points［J］.Ship and Boat，2014（1）：21-24.

［3］ 朱明华.多工况集装箱船配载与堆场翻箱优化研究［D］.上海：上海交通大学，2011. ZHU Minghua.Study on the modeling and optimization of containership stowage planning and pre-marshalling problem under multiple operation modes［D］.Shanghai：Shanghai Jiao Tong University，2011.

［4］ 周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999.

［5］ 权义柯.滚装船车辆配载优化与系统实现［D］.武汉：武汉理工大学，2013. QUAN Yike.The optimization and implementation of Ro-Ro vehicle stowage system［D］.Wuhan：Wuhan University of Technology，2013.

［6］ ZAKERDOOST H，GHASSEMI H，GHIASI M.Ship hull form optimization by evolutionary algorithm in order to diminish the drag［J］.Journal of Marine Science and Application，2013，12（2）：170-179.

［7］ 吕谋，董深，王磊.基于遗传算法的给水管网多工况优化设计［J］.水利学报，2007，38（12）：1507-1511. LV Mou，DONG Shen，WANG Lei.Optimal design of water supply network for multiple operation modes based on genetic algorithm［J］.Journal of Hydraulic Engineering，2007，38（12）：1507-1511.

［8］ 万文，曹平，冯涛.加速混合遗传算法在搜索边坡最危险滑动面中的应用［J］.岩石力学与工程学报，2006，25（增刊1）：2770-2776. WAN Wen，CAO Ping，FENG Tao.Application of accelerating hybrid genetic algorithm to searching for the most dangerous slip surface of slope［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（Supp 1）：2770-2776.

［9］ FOROURAGHI B.Worst-case tolerance design and quality assurance via genetic algorithms［J］.Journal of Optimization Theory and Applications，2002，113（2）：251-268.

［10］ JEONS Y，KIM Y H.A genetic approach to analyze algorithm performance based on the worst-case instances［J］.Journal of Software Engineering and Applications，2010，3（8）：767-775.

［11］ 方陆鹏，富东慧，王忠保，等.连续多跨梁结构模型在力学实验教学中的开发应用［J］.力学与实践，2002，24（3）：60-62. FANG Lupeng，FU Donghui，WANG Baozhong，et al.A continuous multiple-span beam structure model：its design and application in the experimental mechanicscourses［J］.Mechanicsin Engineering，2002，24（3）：60-62.

［12］ 舒恒煜，谭林森.船舶结构力学［M］.武汉：华中理工大学出版社，1993.

Worst-case analysis and optimization of multi-span beams under multiple patch loading

KANG Jiehao1，HE Yuansong2，TAN Kairen2，HE Menghao1，LIU Jun1，CHENG Yuansheng1

1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

2 Marine Design and Research Institute of China，Shanghai 200011，China

The worst-case analysis and optimization design of multi-span beams under multiple patch loading conditions are of vital significance for both ship safety checking and structural weight reducing.In this paper,a method combining the genetic algorithm and finite element analysis is proposed.Specifically, it incorporates the location of the patch loading as a design variable,takes the distance between two patch loadings as the constraint condition,and adopts the maximum bending moment and maximum shear force of each span as the objective function.The method can obtain the worst-case of each span when the multi-span beam is under multiple patch loading conditions.Additionally,this method can be used to adjust the position of support to reduce the maximum bending moment and to optimize the scantling based on the result of worst-case analysis.Numerical results show that a multi-span beam,after the optimization, displays minimal cross-sectional area in each span that satisfies the constraints.Meanwhile,the change of scantling shows little influence on the maximum bending moment and the worst position of patch loading; support position adjustment can reduce the maximum bending moment,thus reducing the structure weight. In an actual project,the support position adjustment reduces 22.64%of the maximum bending moment and 10.55%of the structural weight.

patch loading；multi-span beams；worst-case analysis；optimization design；genetic algorithm

U663.7

A

10.3969/j.issn.1673-3185.2016.06.009

2016-02-02

时间：2016-11-18 15:19

康杰豪，男，1991年生，硕士生。研究方向：结构分析与优化。E-mail：u200912141@163.com程远胜（通信作者），男，1962年生，博士，教授，博士生导师。研究方向：结构分析与优化。E-mail：yscheng@hust.edu.cn

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.018.html 期刊网址：www.ship-research.com

康杰豪，贺远松，谭开忍，等.轮印载荷下多跨梁最危险工况分析与优化［J］.中国舰船研究，2016，11（6）：56-64. KANG Jiehao，HE Yuansong，TAN Kairen，et al.Worst-case analysis and optimization of multi-span beams under multiple patch loading［J］.Chinese Journal of Ship Research，2016，11（6）：56-64.