浸没边界格子Boltzmann方法的改进及转动圆柱绕流模拟

王露，李天匀，朱翔，郭文杰

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2华中科技大学船舶和海洋水动力湖北省重点实验室，湖北武汉430074

浸没边界格子Boltzmann方法的改进及转动圆柱绕流模拟

王露1，2，李天匀1，2，朱翔1，2，郭文杰1，2

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2华中科技大学船舶和海洋水动力湖北省重点实验室，湖北武汉430074

针对浸没边界格子Boltzmann方法计算效率不足的问题，提出一种改进浸没边界格子Boltzmann方法。通过使用作用力格子Boltzmann模型，并简化流固耦合作用力的计算方法，使计算流程得到简化，同时，对比原方法转动圆柱绕流计算结果，计算时间缩短一半以上，提高了数值计算效率。结合改进算法研究转动圆柱绕流的流场升阻力系数、压力系数、流场速度等流体参数场随转速比的关系，揭示了一定的转动圆柱绕流动力学规律。研究结果表明，改进方法准确可靠。

流固耦合；格子Boltzmann方法；浸没边界法；转动圆柱绕流

0 引 言

流体中的圆柱转动是学术研究和实际工程中十分重要的研究对象。圆柱在流体中的运动过程包含在船舶艉轴承推进和轴系冷却等实际工程中。在圆柱绕流的问题中，圆柱绕流一般会产生漩涡脱落并诱发流体的脉动载荷与结构振动。涡激振动不仅对物体造成疲劳，还会对结构造成破坏。针对这些情况，许多学者就如何抑制流体中的涡脱落提出了控制方法，其中圆柱转动就是其中之一。本文将利用转动圆柱绕流的涡脱落现象及升阻力现象的研究成果，开展水润滑轴承的水膜动力学特性分析研究，为轴系振动控制提供基础。

随着数值仿真方法的兴起与发展，对于转动圆柱的流固耦合现象的模拟与研究越发深入。2004年，Feng等［8］首先提出了将格子Boltzmann方法（LBM）［9］与浸没边界法（IBM）［10］相结合的浸没边界格子Boltzmann方法（IB-LBM），并成功地进行了流固耦合仿真。接着Niu等［11］提出了基于动量交换的IB-LBM，Wu等［12］提出了一种隐式速度修正的IB-LBM，然而在一些传统的IB-LBM中，有时在处理流体与固体间的作用力时对网格的尺寸限制较大，有时在处理流体与固体间节点相互作用力时十分复杂，这些局限使得IB-LBM的计算量会增大。Suzuki等［13］提出的相互迭代的IB-LBM方法在处理流固耦合作用力时具有简单的特性，同时，在运动固体的流固耦合模拟中显示出了较高的精度。但此方法在处理流固耦合作用力时需要迭代逼近来保证收敛，会增加计算成本。

针对转动圆柱绕流问题，本文将通过改进流固耦合作用力的计算方式，提出一种简单高效的浸没边界格子Boltzmann方法，并通过转动圆柱绕流模型验证改进方法的有效性及高效性。同时，为了研究转动圆柱绕流的水动力学参数变化特性，本文分别研究Re为40和200时，转动圆柱绕流随转速比变化的流场，及相关流体动力学参数变化的特性，可为工程实际应用提供参考。

1 浸没边界格子Boltzmann法

1.1 格子Boltzmann方法

格子Boltzmann方程描述的是具有离散速度的流体粒子分布函数在固定格点上的运动过程。对于经典格子Boltzmann模型——LBGK模型［14］，在流体碰撞过程中，对应的格子Boltzmann方程表达式为

式中：ωi为离散速度的权系数；u为格点迁移速度；对应的宏观量密度和动量为：

式中，n为离散速度方向的总个数。

式（2）～式（4）构成了经典的LBGK模型。

对于二维D2Q9模型，n为9，其模型离散的速度分布如图1所示，对应的离散速度表达式为：

图1 D2Q9离散速度分布图Fig.1 Discrete speed distribution of D2Q9 model

1.2 浸没边界法

Peskin［10］提出的浸没边界法简化了流固耦合作用力的处理（图2）。在浸没边界法中，对于固体和流体分别采用拉格朗日坐标系和欧拉坐标系进行描述。首先建立描述固体的拉格朗日坐标系，对应的固体节点集为Gh，用X(q ，r，s，t)表示在时间t下的拉格朗日节点，F(q ，r，s，t)为相应时刻固体边界受到的流体作用力，U(X ，t)为固体边界的速度。相应地采用欧拉坐标系描述流场，对应的流体节点集为gh。

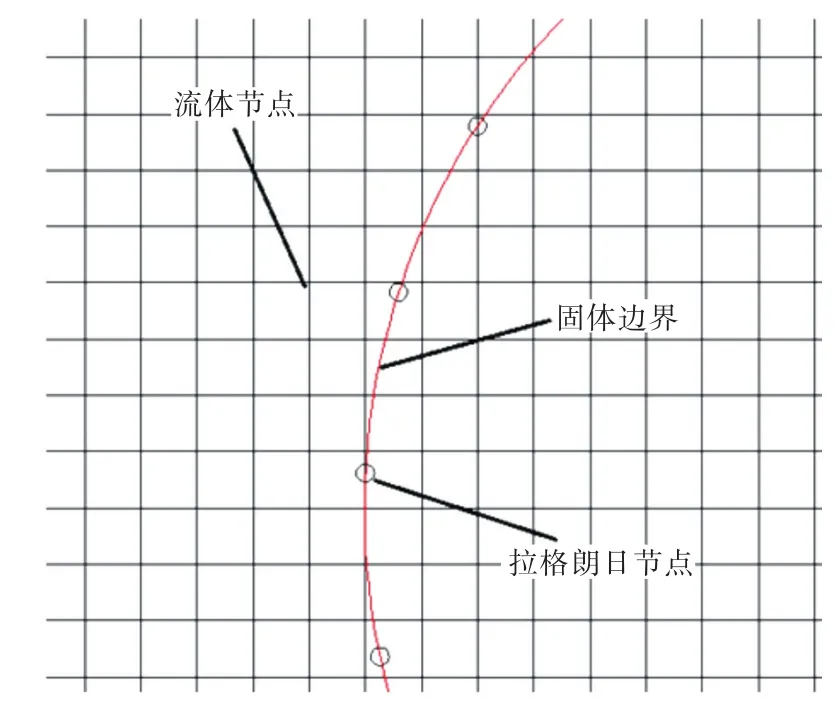
图2 流体及固体边界节点示意图Fig.2 Schematic of fluid and solid boundary

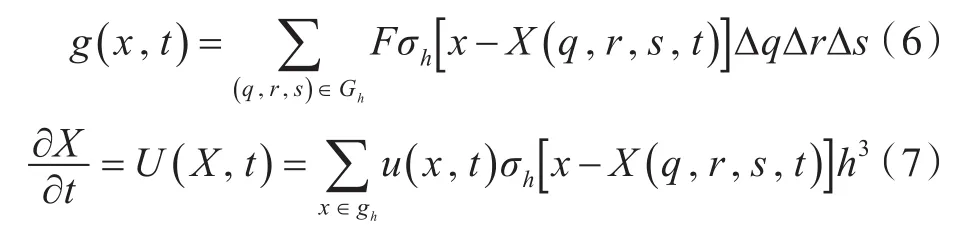
1.3 改进方法

Suzuki等［13］的IB-LBM方法在处理流固耦合作用力时，需采用迭代过程，使得计算速度下降，增加计算时间。其主要原因为在流体演化过程中采用的是标准LBGK模型，并没有考虑流体受到固体作用力的影响，从而使得演化后的流体速度分布函数与实际速度分布函数存在误差。

为了提高计算时流场速度分布函数的计算精度，Guo等［15］在处理Boltzmann方程时，考虑到外力项对流体演化过程的影响，推导出具有二阶精度的作用力格子Boltzmann模型，本文采用该作用力模型处理流场的演化过程，从而提高流场演化过程中的分布函数精度，其对应的方程为

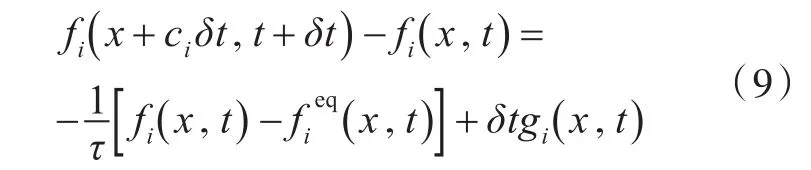
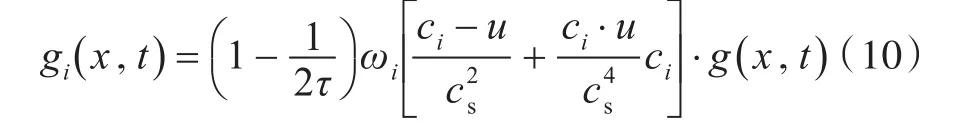
对应的动量表达式为

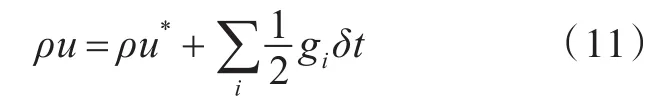
对应的改进方法所采用的拉格朗日节点作用的计算方法如下：

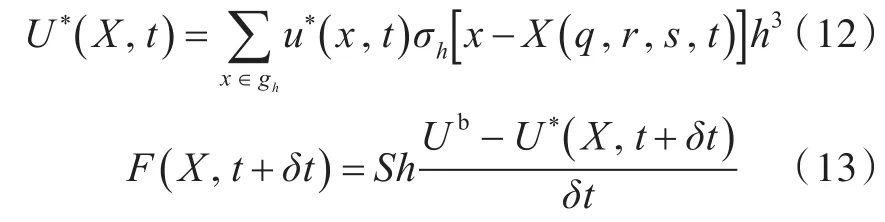
式中：Ub为拉格朗日节点实际迁移速度；Sh为尺度因子。采用了作用力格子Boltzmann模型后，计算步骤如下：

1）给定流场的初始值 ρ，u，利用式（2）计算出对应的初始平衡分布函数计算拉格朗日节点运动变量

2）通过式（9），计算由t到t+δt时刻，流场发生碰撞和迁移过程后的分布函数运用式（3），（4）和（11），计算t+δt时刻对应的ρ，u*和u。

3）通过浸没边界法提供的式（12），计算插值出的拉格朗日边界节点速度U*(X，t+δt)。

5）重复步骤2）～4），直至收敛。

式中：P(s,t)为瞬变电磁场分量；U(s,q)为转换波场分量；s为波场分量对应的时间的场值；t为瞬变电磁场时间；q为波场类时间。

2 转动圆柱绕流模拟

2.1 方法验证

针对改进方法研究转动圆柱绕流模拟，本文仿真过程采用的计算物理模型如图3所示，其中，圆柱转动方向为顺时针，流体沿x正方向流入。流域尺寸为 30D×15D，圆柱圆心坐标为(6.25D，7.5D )，其中D为圆柱直径。考虑到计算精度，圆柱直径D=24δx，仿真过程中选取的格子尺寸δx=δt=1。流域的边界条件为：左边入口u=U，v=0；右边出口即沿x方向速度不变；上下边界即沿 y方向速度不变，其中U=0.1，为流域入口速度。为了处理格子Boltzmann碰撞迁移过程的边界条件，流场边界采用的是非平衡态外推边界条件［16］。对于圆柱边界将其等分为120段。

图3 仿真计算模型Fig.3 Simulation model

计算圆柱在流场中所受到的升阻力时，直接取为拉格朗日节点所受的流体作用力。相对应的阻力系数和升力系数可表示为：

式中：Cd，Cl分别为阻力系数和升力系数；Fx，Fy分别为拉格朗日节点作用力F在 x方向和 y方向上的分量。

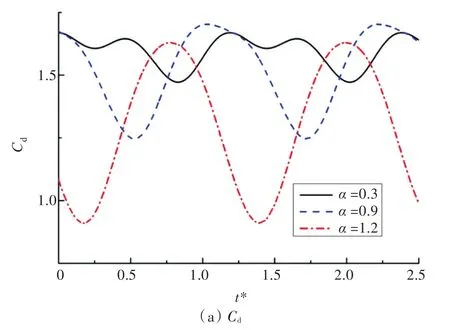
图4为雷诺数Re=200，转速比α分别为0.5，1，1.5时，圆柱升阻力系数关系曲线，对比左侧的涡量云图，可以发现圆柱尾部涡量随着转速比的增加圆柱尾涡逐渐下移。随着转速比的增加，圆柱的升阻力系数曲线逐渐变化为椭圆形，这一曲线变化现象与Mittal等［17］的有限元仿真结果一致。

图4 Re=200，α分别为0.5，1，1.5时涡量云图及圆柱升阻力曲线Fig.4 Vorticity contours and the drag coefficient-lift coefficient line of flow over rotating cylinder when Re is 200，αis 0.5,1.0,1.5

图4右侧的升阻力系数关系曲线，是由计算稳定后，10 000时间步下的数值点构成，由多周期曲线构成。从图中可以看出，不同周期下的节点在相同位置重合，表明改进算法计算结果稳定。

表1 圆柱阻力系数和升力系数比较Tab.1 Comparison between drag coefficient and lift coefficient

表1为不同转速比下，本文的模拟结果与邬小军等［18-19］采用格子Boltzmann方法仿真的升力系数和阻力系数对比。比较表1中给出的4组数据，改进算法采用的是浸没边界法计算固体边界受力，而另外3种算法则采用的是3种不同的LB曲面边界处理格式，分别为统一边界法（YMS）、非平衡态外推格式法和反弹边界条件法，由于这些边界条件的处理方式均采用数值插值格式方式计算固体边界流场的速度分布，在计算过程中会产生误差，而固体表面受力计算过程是通过固体表面流场速度分布变化（浸没边界法）或固体表面流场动量分布变化（格子Boltzmann方法）计算，从而会进一步产生数值误差，导致各文献间的数据存在一定误差。但从表中数据可发现，升力系数与阻力系数变化趋势基本吻合，对应的幅值变化也基本一致，表明通过与退化为格子Boltzmann方法计算的结果对比，本文的改进方法在转动圆柱绕流仿真的可行性得到验证。

为进一步验证本文的改进方法在转动圆柱绕流中的有效性，将本方法计算流场结果与Yu等［20］基于格子Boltzmann方法提出的YMS的计算结果进行对比。图5给出了转速比α=0.5时，当流场稳定后，半个周期内不同时刻，在圆心高度上，从圆柱边界到圆心2个直径范围内的速度分布。从图中可以看出，二者在x及y方向不同时间的速度分布结果十分接近，这也进一步验证了本方法的在转动圆柱绕流仿真中的有效性。

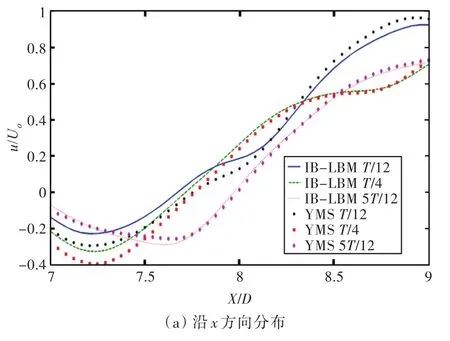
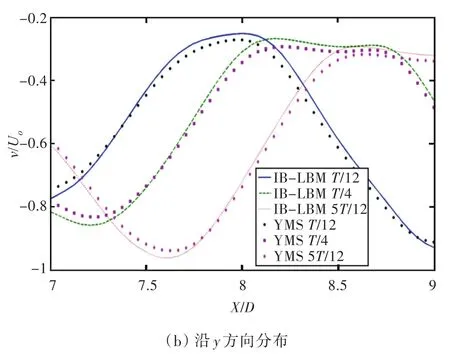
图5 Re=200，α=0.5，圆柱后方速度分布曲线Fig.5 The velocity distribution of flow over rotating cylinder when Re is 200，α is 0.5

为比较改进计算方法与原方法的计算效率，本文模型仿真的电脑参数为CPU为E5-2650 V2 2.6 GHz，内存为128 GB，在2012a版本的Matlab上仿真2种方法的转动圆柱绕流。表2为Re为40和200，α=0.5这2种工况下，为保证计算收敛时仿真计算时间对比表。对比2组计算数据可以发现，相同循环次数下，改进计算方法所需计算时间缩短了一半以上，这充分体现了改进方法计算效率上的优势。

表2 Re为40和200计算模型对应的计算时间对比Tab.2 Comparison of the calculating time for flow over a cylinder when Re is 40 and 200

2.2 计算结果

图6为不同转速比下，Re=200时，圆柱阻力系数、升力系数随时间变化的曲线。观察图6（a）和图6（b）中曲线的变化过程，可以发现当转速比α＜1.0时，阻力曲线后半周期中对应处的波谷会逐渐上移。当α＞1.0后圆柱阻力曲线周期会增大到约为原来的2倍，即原来的波谷出现消失。圆柱的阻力系数幅值明显增大，平均阻力系数也明显减小，随着转速比的增大圆柱受到的升力逐渐增大。随着转速比的增加，圆柱的升力系数曲线逐渐向上平移，幅值并没有观察到明显变化。同时对比各条曲线的波谷波峰可以发现，各曲线的相位并不相同，这是由于圆柱转动产生的相位滞后。

为研究圆柱表面正压力在圆柱表面的分布与转速比的关系，引入圆柱表面压力系数Cp作为研究参数。其表达式为

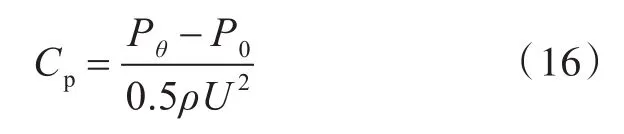
式中：Pθ为圆柱表面θ处的压力；P0为无穷远处来流压力。

图7是Re为40和200时，本文和Suzuki［13］这2种计算方法计算的不同转速比下的圆柱表面压力系数分布。由图中的峰值曲线可以看出，2种计算结果的压力系数分布十分接近，即本计算方法有效。角度接近90°在圆柱正下方时圆柱表面压力系数最小，且随着转速比的增大峰值出现明显变化，这与实际的流场压力分布变化一致。

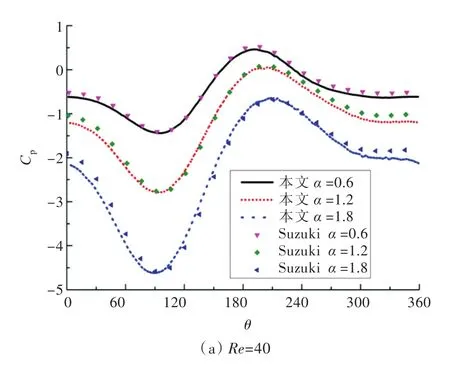
图7 Re为40和200的不同转速比下，圆周表面压力系数分布Fig.7 The pressure coefficient along the cylinder surface when Re is 40 and 200 with differentα

图8为升阻力系数随转速比变化曲线。随着α增大，当升力系数较小且α＜0.5时，阻力系数并没有明显改变，当1.0＜α＜2.4时，阻力系数呈近似线性减小，同时升力系数随转速比增加呈线性变化，但Re为200与40的计算结果相比较，阻力系数变化更剧烈，这一变化趋势与Mittal等［17］的有限元仿真结果一致。

图8 Re为40和200时圆柱升阻力系数随转速比变化Fig.8 The drag coefficient and lift coefficient of flow over a rotating cylinder when Re is 40 and 200 with differentα

3 结 语

本文通过结合作用力格子Boltzmann模型和Suzuki等［13］浸没边界法模型，提出了一种计算效率更高的浸没边界格子Boltzmann改进算法。通过转动圆柱绕流的模型，对比不同文献与本方法的仿真结果的阻力系数、升力系数及流场分布等流体动力学参数，证明了改进计算方法的有效

性。同时，对比不同雷诺数转动圆柱绕流计算时间，发现改进计算方法节省一半以上的时间，充分说明改进算法高效。针对转动圆柱绕流进行了仿真，并对随转速比变化的流体动力学参数变化进行了分析，其结果可为相关的工程应用提供参考。

［1］ PRANDTL L.The magnus effect and wind-powered ships［J］.Naturwissenschaften，1925（13）：93-108

［2］ TOKUMARU P T，DIMOTAKIS P E.The lift of a cylinder executing rotary motions in an uniform flow［J］. Journal of Fluid Mechanics，1993（255）：1-10.

［3］ CHEN Y M，OU Y R，PEARLSTEIN A J.Development of the wake behind a circular cylinder impulsively started into rotatory and rectilinear motion［J］.Journal of Fluid Mechanics，1993（253）：449-484.

［4］ CHEW Y T，CHENG M，LUO S C.A numerical study of flow past a rotating circular cylinder using a hybrid vortex scheme［J］.Journal of Fluid Mechanics，1995（299）：35-71.

［5］ KANG S，CHOI H，LEE S.Laminar flow past a rotating circular cylinder［J］.Physics of Fluids（1994 present），1999，11（11）：3312-3321.

［6］ 何颖，杨新民，陈志华，等.旋转圆柱绕流的流场特性［J］.船舶力学，2015，19（5）：501-508. HE Ying，YANG Xinmin，CHEN Zhihua，et al.Flow field characteristics of flow past a rotating cylinder［J］. Journal of Ship Mechanics，2015，19（5）：501-508.

［7］ 赫鹏，李国栋，杨兰，等.圆柱绕流流场结构的大涡模拟研究［J］.应用力学学报，2012，29（4）：437-443. HAO Peng，LI Guodong，YANG Lan，et al.Large eddy simulation of the circular cylinder flow in different regimes［J］.Chinese Journal of Applied Mechanics，2012，29（4）：437-443.

［8］ FENG Z G，MICHAELIDES E E.The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems［J］.Journal of Computational Physics，2004，195（2）：602-628.

［9］ SUCCI S.The lattice Boltzmann equation：for fluid dynamics and beyond［M］.Oxford：Oxford University Press，2001.

［10］ PESKIN C S.The immersed boundary method［J］.Acta Numerica，2002，11：479-517.

［11］ NIU X D，SHU C，CHEW Y T，et al.A momentum exchange-basedimmersedboundary-latticeBoltzmann method for simulating incompressible viscous flows［J］.Physics Letters A，2006，354（3）：173-182.

［12］ WU J，SHU C.Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications［J］.Journal of Computational Physics，2009，228（6）：1963-1979.

［13］ SUZUKI K，INAMURO T.A higher-order immersed boundary-lattice Boltzmann method using a smooth velocity field near boundaries［J］.Computers and Fluids，2013，76：105-115.

［14］ QIAN Y H，D'HUMIÈRES D，LALLEMAND P.Lattice BGK models for Navier-Stokes equation［J］.Europhysics Letters，1992，17（6）：479-484.

［15］ GUO Z L，ZHENG C G，SHI B C.Discrete lattice effects on the forcing term in the lattice Boltzmann method［J］.Physical Review E，2002，65（4）：046308.

［16］ GUO Z L，ZHENG C G，SHI B C.Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method［J］. Chinese Physics，2002，11（4）：366-374.

［17］ MITTAL S，KUMAR B.Flow past a rotating cylinder［J］.Journal of Fluid Mechanics，2003，476：303-334.

［18］ 邬小军.静止和转动圆柱绕流的格子Boltzmann模拟［D］.武汉：华中科技大学，2009. WU Xiaojun.The lattice Boltzmann method simulation of the flow past static and rotating circular cylinder［D］.Wuhan：Huazhong University of Science and Technology，2009

［19］ YAN Y Y，ZU Y Q.Numerical simulation of heat transfer and fluid flow past a rotating isothermal cylinder-a LBM approach［J］.International Journal of Heat and Mass Transfer，2008，51（9/10）：2519-2536.

［20］ YU D Z，MEI R W，SHYY W.A unified boundary treatment in lattice Boltzmann method［C］//Proceedings of the 41st Aerospace Sciences Meeting and Exhibit.Reno，Nevada：AIAA，2003.

Improved immersed boundary lattice Boltzmann method and simulation of flow over rotating cylinder

WANG Lu1，2，LI Tianyun1，2，ZHU Xiang1，2，GUO Wenjie1，2

1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

2 Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics，Huazhong University of Technology and Science，Wuhan 430074，China

Based on Suzuki's immersed boundary lattice Boltzmann method,an improved approach is proposed.By adopting the force model of the lattice Boltzmann method and improving the technique of fluid structure interaction force calculation,the process of calculating the force of fluid structure interaction is simplified.Moreover，its calculation time is over 50%shorter than that of the original method,which means that efficiency is greatly improved.Based on the improved method,such features as lift coefficient,drag coefficient，pressure coefficient and flow field are discussed under different conditions of flow over a rotating cylinder.Compared with the related results,this new improved method is shown to be accurate and reliable.

fluid structure interaction；lattice Boltzmann method；immersed boundary method；flow around rotating cylinder

U661.1

A

10.3969/j.issn.1673-3185.2016.06.015

2015-12-17

时间：2016-11-18 15:19

国家自然科学基金资助项目（51379083，51479079，51579109）；高等学校博士学科点专项科研基金资助项目（20120142110051）

王露，男，1991年生，硕士生。研究方向：船舶与海洋结构物设计制造。E-mail：1229398383@qq.com李天匀（通信作者），男，1969年生，教授，博士生导师。研究方向：结构振动噪声分析。E-mail：ltyz801@hust.edu.cn

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.030.html 期刊网址：www.ship-research.com

王露，李天匀，朱翔，等.浸没边界格子Boltzmann方法的改进及转动圆柱绕流模拟［J］.中国舰船研究，2016，11（6）：97-103. WANG Lu，LI Tianyun，ZHU Xiang，et al.Improved immersed boundary lattice Boltzmann method and simulation of flow over rotating cylinde［rJ］.Chinese Journal of Ship Research，2016，11（6）：97-103.