模型准确性对系统管网泄漏诊断的影响分析

刘倩，张扬，徐新华，谢军龙，王飞飞，严天

1华中科技大学环境科学与工程学院，湖北武汉430074

2中国舰船研究设计中心，湖北武汉430064

3华中科技大学能源与动力工程学院，湖北武汉430074

模型准确性对系统管网泄漏诊断的影响分析

刘倩1，张扬2，徐新华1，谢军龙3，王飞飞1，严天1

1华中科技大学环境科学与工程学院，湖北武汉430074

2中国舰船研究设计中心，湖北武汉430064

3华中科技大学能源与动力工程学院，湖北武汉430074

针对基于压力敏感性的管网泄漏诊断方法应用中由管网模型误差带来的鲁棒性问题，提出根据量化的模型准确度指标来分析诊断方法的有效性。利用FlowMaster流体仿真软件建立某实际冷却系统管网不同准确度下的水力模型。以该管网的标定模型为基准，采用改进的灰色关联度分析（IGR2）法对各模型与基准模型间各测点压力值的相似性进行评估来计算误差，得到模型准确度量化指标。采用故障诊断成功率（FDSP）计算泄漏诊断的有效性。基于不同准确度的管网模型进行泄漏诊断分析，获得不同准确度模型对泄漏诊断有效性的影响。结果表明，该泄漏诊断法的有效性随模型准确度的增大而提高，当管网模型准确度大于0.75时，故障诊断成功率均处于90%以上，说明该故障诊断方法对模型误差具有一定的鲁棒性。

系统管网；泄漏诊断；压力敏感性分析；模型误差；模型准确度量化；FlowMaster软件

0 引 言

随着现代管网系统复杂化及自动化程度的提高，故障的发生难以避免，为保证系统安全可靠运行，对故障做出准确迅速的诊断以及时排除故障就显得尤为重要［1-3］。对于市政管网、船舶冷却水管网等，泄漏是管网故障中的常见问题，这种现象不仅会导致资源浪费，还有可能引发重大事故。

基于压力敏感性分析或状态空间等数学模型的城市供水、石油燃气管网、空调水系统等管道泄漏故障检测与定位是一种间接法［4-7］。这是一种将泄漏引起的压力、流量等流体参数的测量值与模型预测值相对比进行泄漏故障诊断的方法。基于模型的故障诊断方法需要建立系统的数学模型，然而由于系统的一些参数（如阻力特性等）难以准确确定且真实系统的干扰与噪声特性难以准确描述，因此数学模型难以非常准确地描述真实系统。即使系统零故障，数学模型也必然存在误差。为克服模型不确定性产生的影响，基于模型的故障诊断方法需要具有很好的鲁棒性，即降低诊断结果对模型不确定性的敏感程度同时又保证模型对故障有一定的敏感性。目前提高鲁棒性的方法一般是采用通过阈值过滤模型不确定性［6，8］、未知输入观察器或本征结构分配［9］等。

基于模型的故障诊断鲁棒性问题涉及模型误差、噪声及干扰等。目前，对模型误差的衡量仍缺乏统一体系［10-11］，主要方法有相对偏差、残差平方和法［12］等误差分析法，以及灰色关联理论［11-14］、基于时间序列的线性回归、频谱分析［15］和基于统计数据的ED检验、置信区间等［16］方法，或者采用不同方法的加权综合［17-18］。对水管网模型的模型误差主要通过监测点的压力、流量的实测值与模型模拟值的误差大小进行统计，通过管网实际压力分布与模拟是否吻合等方面来评估［19-20］。

模型误差较大会影响诊断的鲁棒性，但实际应用中模型越准确，需要付出的成本越高，实现起来越困难，因此有必要分析模型准确性对该泄漏诊断方法有效性的影响。本文提出用故障诊断成功率（Fault Diagnosis Success Percent，FDSP）来量化泄漏诊断方法的有效性，采用改进的灰色关联度分析（Improved Grey Relational Analysis，IGR2）法进行管网模型准确性的量化分析。根据管网模拟结果，分析管网模型准确性对故障诊断成功率的影响。结果表明，数学模型的准确性对诊断结果有明显的影响，同时基于压力敏感性模型的诊断方法对模型误差具有一定的鲁棒性。

1 系统描述与模型

某电子设备集中冷却水闭式系统如图1所示。本文研究对象为该冷却水管网的某大支路系统，该支路系统的设计流量为8 m3/h，由16个用户支路组成，各用户支路均设有1台电子设备，且所有设备的额定流量均为0.5 m3/h。16个小支路编号依次为Z1～Z16，按照并联方式连接，用户支路管径均为DN20。每个支路两端均设有1个压力测点。16个小支路共计32个压力测点（位于管网节点）编号为P1～P32。所安装压力传感器量程为0.8 MPa，精度为0.5%。水泵的流量为18 m3/h，扬程为60 mH2O。大支路的主干管上设有流量传感器及压差传感器（即压力测点P0-1与P0-2）。回水干管上装设有静态流量平衡阀，用于调节大支路间的流量平衡。各用户支路设有截止阀和球阀，可分别调节支路开关及阻力平衡。管网管道材质为不锈钢管，管道内介质为乙二醇防冻液。

本研究采用FlowMaster进行管网流动特性仿真。为简化描述和分析，将图1的整个水系统进行简化，在总供回水管间设置水泵及支路阻力件（模拟其他支路损失）。管网模型如图2所示。模型根据现场实测各管段的长度、管径、阀件（阀门、三通、弯头）数量及压力测点布置位置等建立。根据现场实测数据对模型各元件进行阻力系数调节，得到标定模型。模型通过元件流量源加载负流量来模拟管网漏水。

2 故障诊断成功率

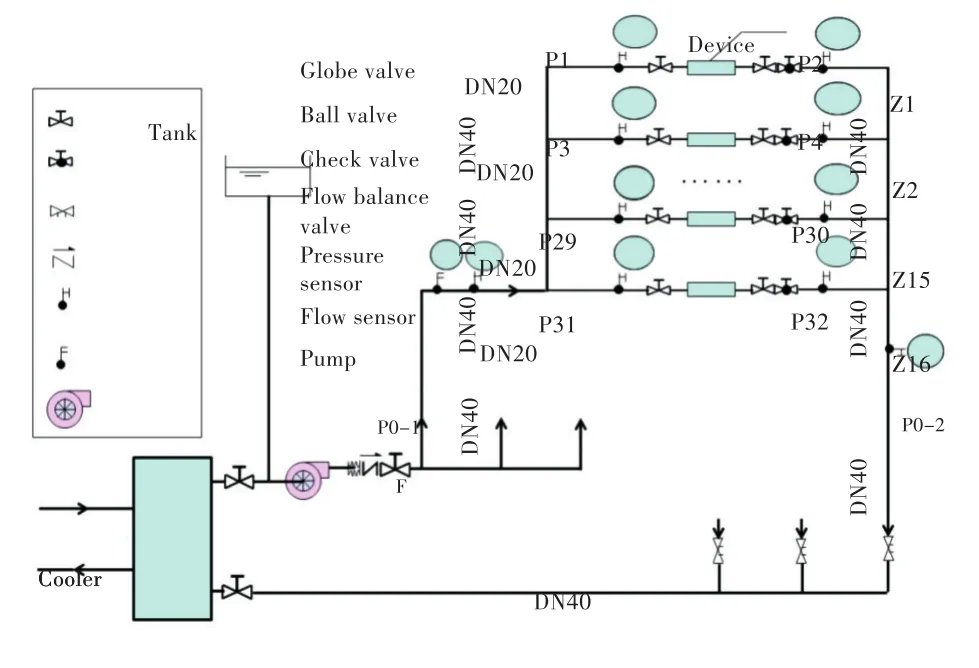
图1 冷却水系统示意图Fig.1 Schematic of refrigerant system and measurement

本文采用基于压力敏感性模型的诊断方法对冷却水系统的泄漏故障进行分析。基于压力敏感性模型的诊断方法是通过对比系统现有测量数据与系统模型预测数据产生的余差和相应的分析来确定系统故障的方法［4，21］。该方法通过管网压力

敏感性分析获得不同泄漏故障方案下的敏感性矩阵，并采用相关性函数法对实测余差向量与敏感性矩阵进行相关性分析，获得实际泄漏故障信息（即余差向量）与泄漏故障方案信息（即敏感性矩阵）二者的相关性系数，最后根据相关性系数大小诊断出泄漏点所在位置或附近区域。相关性系数值越大，对应的泄漏点出现泄漏的可能性就越大。建立余差向量及敏感性矩阵需要管网的运行数据。管网在正常运行及泄漏时的压力分布可由系统正常运行或人为引入泄漏故障的实际测量获取。但是在实际工程应用中引入人为泄漏故障成本高、影响大，一般难以引入人为泄漏故障。通常的做法是根据实际系统的测量数据来对系统模型进行标定，再采用标定后的模型并人为在模型中引入故障信息以模拟获取系统的运行参数。在获得不同泄漏故障方案下的敏感性矩阵后，再根据实际系统的运行参数计算余差向量并与建立好的敏感性矩阵进行相关性分析，最后进行泄漏故障的诊断。

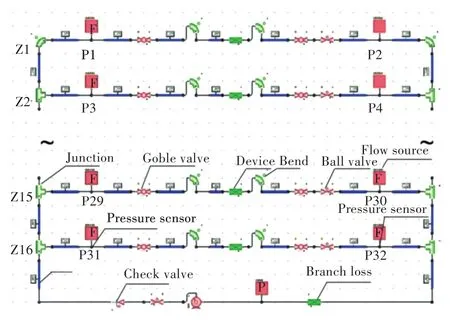
图2 冷却水系统管网仿真模型Fig.2 Simulation model of refrigerant system network

故障诊断的有效性通过计算故障诊断成功率FDSP进行衡量。FDSP是指某处出现一定泄漏量的泄漏时，故障诊断方法能够有效实现泄漏点位置诊断的概率，由式（1）计算得到。

式中，nf与nfs分别为不同泄漏情形总数与成功诊断的泄漏情形个数。

通过诊断得到泄漏点位置与管网实际泄漏点的距离来评价某故障方案是否实现成功诊断，并按照诊断满意度将FDSP划分为理想、满意与可接受3类。

1）FDSP1——理想：诊断的泄漏点位置（相关系数最大值）位于实际故障点的概率。

2）FDSP2——满意：诊断的泄漏点位置（相关系数最大值）位于实际故障点相邻支路上及以内（离实际故障点位置不超过1条支路的距离）的概率。

3）FDSP3——可接受：诊断的泄漏点位置（相关系数最大值）位于实际故障点间隔1条支路上及以内（离实际故障点位置不超过2条支路的距离）的概率。

本文泄漏诊断中管网正常运行时的各压力测点值以及在系统泄漏时（单泄漏点）的各压力测点值由FlowMaster建立的冷却水系统管网模型模拟得到。考虑可能的泄漏点j为管网节点（压力测点）P1～P32，对应32种故障方案f（jk），管网标称漏水量f=1 m3/h。假定管网各支路用户流量及实际漏水量均恒定，某时刻实际泄漏点分别位于P4，P19时计算得到的各故障方案对应的泄漏点相关系数 ρ及泄漏点（P1～P32）位置分布如图2和图3所示。图中，圆点表示泄漏点，颜色越深的点表示由该泄漏点得到的相关系数ρ值越大，则该节点出现泄漏的可能性越高。由图2可知，管网中最可能的泄漏点为P2，位于实际泄漏点P4相邻支路上，则该诊断结果属于满意型及可接受型；由图3可知，管网中最可能的泄漏点为P19，与实际泄漏情况吻合，则该诊断结果仅属于理想型。

3 模型准确性量化分析

模型准确性量化方法主要有传统管网精度评价法［19］、残差平方和法［12］、数值相似度与曲线相似度综合法［18］以及IGR2方法［19］。IGR2法能更有效、精确地评价模型的准确性。该方法的实测值y（k）与模拟值的相似度γ的计算公式如式（2）～式（4）所示。

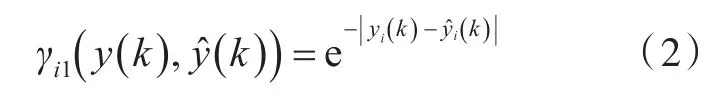
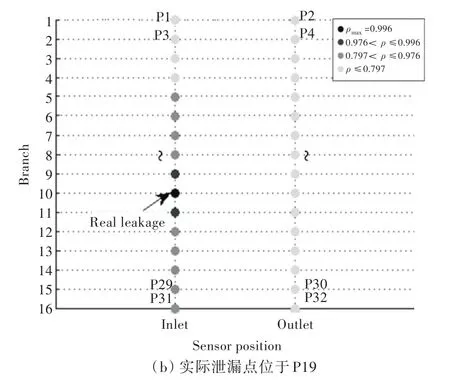
图3 泄漏点（P1～P32）对应相关系数ρ分布及压力测点位置示意图Fig.3 Distribution of correlationρcoincident to leakages（P1～P32）and pressure sensor position

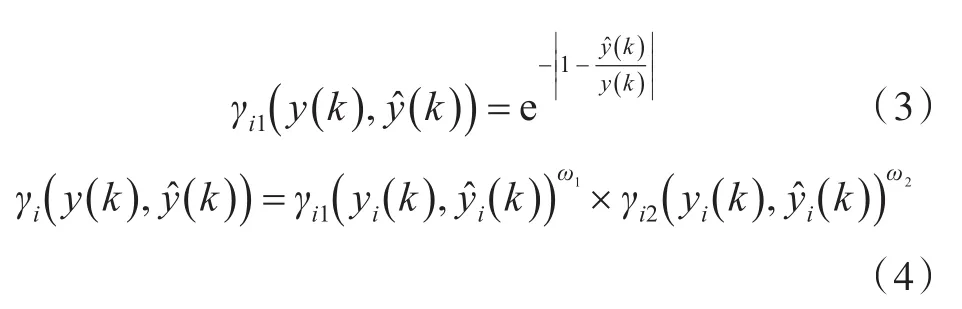
式中：γ1为序列（含i个值）的几何相似性评估指标；γ2为序列（含i个值）的距离接近性评估指标；ω1，ω2为二者的权重系数，且满足ω1+ω2=1，通常取ω1=ω2=0.5。

本研究对不同模型干管均加载同一流量，以各测点压力模拟值与压力实测值的相似度作为模型准确度。管网的流量分配及运行工况等水力特性由各管段与各用户的阻力系数决定，因而模型准确度可通过各管段与用户的阻力系数来衡量。本研究系统中的压力监测点（P1～P32）位于各用户支路进出口（即干管与用户支路的交接处），由实测数据得知各干管管段阻力系数很小，因此干管阻力系数模拟值与实际偏差可忽略不计。当保证模拟管网模型与实际管网的总流量相等时，若模拟管网模型与实际管网P1～P32的压力均分别相等，由于干管阻力系数近似相等，则模拟管网与实际管网各干管上的流量分别基本相等，即管网各用户支路流量基本相等，因而两模型用户支路的阻力系数也基本相等，说明两模型完全吻合。

以FlowMaster建立的冷却水系统管网标定模型为标准模型，调节标定模型的设备及管道等支路阻力件的阻力系数偏差（偏差为随机值，偏差上限分别为±1%，±5%和±10%等）得到准确度不同的模型。保证管网供水流量与实测值条件相同（管网实测总流量为8.02 m3/h，各模型总流量误差均为±0.05%以内），获得管网各压力测点压力的模拟值，采用IGR2法计算其模型准确度MA，以某模型部分压力测点P11～P16为算例说明具体过程。计算结果如表1所示（n为压力测点数）。

表1 模型准确度计算结果Tab.1 Model accuracy calculation results

当权重系数ω1和ω2取不同值时，各模型的准确度计算结果如表2所示，表中还给出了压力模拟值（不同准确度模型的模拟值）与实测值（即标定模型的模拟值）的偏差分别低于±40，±20与±10 kPa的压力测点数占监测点总数的比例。管网各压力监测点的实测值与模拟值的偏差为序列的距离接近性，管网压力分布则为序列的几何相似性。IGR2法能同时衡量各监测点压力的数值相似性和几何相似性，因而能够作为管网模型准确度评价指标。由表2可知，当各监测点压力值的几何相似性的权重系数ω1分别取0.2，0.5和0.8时，IGR2法计算得到的模型准确度大体随着管段阻力偏差的增大而减小。当ω1=0.8时，管网阻力的偏差范围为±20%，模型准确度为0.368 5，显著低于管网阻力偏差更大的模型，因为此时模型准确度倾向于管网的压力分布特性，单个测点压力偏差的影响大大减小，造成模型准确度较低，因此权重系数应根据具体应用合适选取。

4 模型对管网泄漏诊断的影响分析

以上述管网标定模型为标准模型，调节标定模型的设备及管道等支路阻力件的阻力系数，得

到不同准确度的模型。保证管网供水流量与实测值条件相同（流量为8.02 m3/h，误差为±0.05%以内），采用IGR2法（ω1=0.5）计算其模型准确度（压力单位为kPa）。

表2 基于IGR2法的模型准确度Tab.2 Model accuracy based on IGR2 method

管网实际泄漏点分别位于P1～P32（实际泄漏量均为1 m3/h）泄漏情形下的各压力测点的实测值由该标定模型计算得到（暂不考虑系统干扰与噪声）。基于各不同准确度的模型对32种泄漏情形（nf=32）下的泄漏位置进行诊断，得到不同模型的故障诊断成功率FDSP1，FDSP2及FDSP3（标称泄漏量均为1 m3/h），如图4所示。结果表明，随着模型准确度的提高，故障诊断成功率FDSP1，FDSP2及FDSP3均呈现逐渐增大的趋势。当该管网模型准确度指标MA处于0.75～1范围内时，诊断的泄漏点位于实际故障点（FDSP1）或相邻支路以内（FDSP2）以及位于实际故障点间隔1条支路以内的概率（FDSP3）基本均高于90%，模型准确度对诊断方法的有效性影响不大，说明此范围内该诊断方法对模型误差的鲁棒性较好。当模型准确度小于0.75时，随着模型准确度的下降，诊断有效性大大下降；当准确度指标MA低至0.50左右时，诊断的泄漏点与实际故障点距离不超过2条支路的概率基本均低于60%，此时难以保证该泄漏诊断方法的有效性。

图4 模型准确度对管网泄漏诊断成功率的影响Fig.4 Effects of model accuracy on FDSPs of pipe network system

5 结 语

对于基于模型的泄漏诊断方法，模型准确度的影响十分重要。在实际应用中，模型准确性越高，成本越高，过低则可能造成诊断结果不准确。目前，泄漏诊断方法通常仅为定性评价，模型准确性也缺乏统一的评估体系，造成衡量模型对泄漏诊断方法的影响较为困难。本文对基于某实际冷却系统建立的FlowMaster管网模型采用IGR2法进行测点压力相似性评估，得到不同精度模型的准确度指标及当管网各测点压力偏差与压力分布权重不同时的准确度指标对比，结果显示，准确度指标MA能有效反映模型的实际准确性。在此基础上，本文基于该冷却水系统管网不同MA指标的模型进行泄漏诊断，由故障诊断成功率FDSP评价诊断结果，分析了模型准确性对泄漏诊断方法诊断有效性的影响。结果显示，模型准确性越高，诊断有效性越好，准确性过低则很难保证诊断的有效性。当权重系数ω1=0.50、计算得到的模型准确度指标MA≥0.75时（各管段阻力偏差为±15%以内），诊断的泄漏点与实际故障点距离较近（不超过2条支路）的概率基本均达到90%以上，此时该泄漏诊断方法结果较理想，同时该范围内诊断方法对模型误差的鲁棒性较好。

［1］ 李霞.城市供水管网漏损定位及控制研究［D］.天津：天津大学，2006.

［2］ FRANK P M.Fault diagnosis in dynamics systems using analytical and knowledge-based redundancy：a survey and some new results［J］.Automatica，1990，26（3）：459-474.

［3］ 马欢.管道泄漏检测与定位技术国内外研究现状［J］.科教文汇，2007（2）：208，90.

［4］ QUEVEDO J，CUGUERÓ M，PÉREZ R，et al.Leakage location in water distribution networks based on correlation measurement of pressure sensors［C］//IWA

Symposium on Systems Analysis and Integrated Assessment.San Sebastián：International Water Association（IWA），2011：290-297.

［5］ PÉREZ R，PUIG V，PASCUAL J，et al.Methodology for leakage isolation using pressure sensitivity analysis in water distribution networks［J］.Control Engineering Practice，2011，19（10）：1157-1167.

［6］ MESEGUER J，MIRATS-TUR J M，CEMBRANO G，et al.A decision support system for on-line leakage localization［J］.Environmental Modelling&Software，2014，60：331-345.

［7］ PENG Y，YOUSSOUF A，ARTE P，et al.A complete procedure for residual generation and evaluation with application to a heat exchanger［J］.IEEE Transactions on ControlSystemsTechnology，1997，5（6）：542-555.

［8］ GERTLER J.Fault detection and diagnosis in engineering systems［M］.Florida：CRC Press，1998.

［9］ CHEN J，PATTON R J.Robust model-based fault diagnosis for dynamic systems［M］.New York：Springer US，1999.

［10］ 舒诗湖.基于不确定性分析的供水管网模型精度评估［J］.城镇供水，2014（3）：58-60. SHU Shihu.Accuracy evaluation of water supply network model based on uncertainty analysis［J］.City and Town Water Supply，2014（3）：58-60.

［11］ 宁小磊，吴颖霞，陈战旗.一种改进的灰色关联模型验证方法研究［J］.计算机仿真，2015，32（7）：259-263. NING Xiaolei，WU Yingxia，CHEN Zhanqi.Study on validation of simulation models based on improved gray relational analysis［J］.Computer Simulation，2015，32（7）：259-263.

［12］ 杜坤.供水管网水力模型校核与漏损定位研究［D］.重庆：重庆大学，2014.

［13］ 邓聚龙.灰色系统综述［J］.世界科学，1983（7）：1-5.

［14］ 刘金英.灰色预测理论与评价方法在水环境中的应用研究［D］.吉林：吉林大学，2004.

［15］ 李鹏波，谢红卫.频谱分析方法在仿真可信性研究中的应用［J］.系统仿真学报，1998（3）：18-21，54. LI Pengbo，XIE Hongwei.Application of spectrum analysis in the research of simulation model credibility［J］.Journal of System Simulation，1998（3）：18-21，54.

［16］ 李小龙，关晓东.系统仿真模型精度的分析与验证［J］.西北工业大学学报，1999，17（2）：290-294. LI Xiaolong，GUAN Xiaodong.On improving model precision of simulation system［J］.Journal of Northwestern Polytechnical University，1999，17（2）：290-294.

［17］ 刘胜，李莉红.船舶电力推进系统仿真可信度FCE评估方法研究［J］.自动化技术与应用，2012，31（4）：52-57. LIU Sheng，LI Lihong.Application of FCE for credibility of simulation of ship electric propulsion system［J］.Techniques of Automation and Applications，2012，31（4）：52-57.

［18］ 刘觉民，宋海燕，鲁文军，等.模拟原动系统模型的仿真准确度评估［J］.电源技术，2013，37（3）：433-435，484. LIU Juemin，SONG Haiyan，LU Wenjun，et al.Assessment on simulation accuracy of models of prime mover system simulator［J］.Chinese Journal of Power Sources，2013，37（3）：433-435，484.

［19］ 舒诗湖，赵明，何文杰，等.供水管网水力、水质模型校核标准探讨［J］.中国给水排水，2008，24（18）：104-106. SHU Shihu，ZHAO Ming，HE Wenjie，et al.Discussion on calibration standard for hydraulic and water quality model of water distribution network［J］.China Water&Wastewater，2008，24（18）：104-106.

［20］ 詹健，贾俊松.遗传编码方式对管网水力模拟准确度的影响分析［J］.南昌大学学报（工科版），2007，29（1）：78-82. ZHAN Jian，JIA Junsong.Different influence on accuracy of hydraulic simulation of pipe networks by different genetic coding modes［J］.Journal of Nanchang University（Engineering&Technology），2007，29（1）：78-82.

［21］ 刘倩，张扬，徐新华，等.基于压力敏感性分析的集中冷却系统泄漏诊断［J］.中国舰船研究，2016，11（5）：128-133. LIU Qian，ZHANG Yang，XU Xinhua，et al.Pressure sensitivity analysis-based leakage diagnosis of centralized refrigerant system for electronic devices［J］.Chinese Journal of Ship Research，2016，11（5）：128-133.

Effect analysis of model accuracy on leakage diagnosis of pipe network system

LIU Qian1，ZHANG Yang2，XU Xinhua1，XIE Junlong3，WANG Feifei1，YAN Tian1

1 School of Environmental Science&Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

2 China Ship Development and Design Center，Wuhan 430064，China

3 School of Energy and Power Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

This paper proposes an evaluating method for the effectiveness of leakage diagnosis by using quantitative index of model accuracy，aiming at the pressure sensitivity analysis-based leakage diagnosis method of the pipe network brought by model mismatch.FlowMaster software is used to establish the pipe network models with different accuracy of a real refrigerant system.Regarding the calibrated model as the benchmark of the pipe network，the improved Grey Relational Analysis（IGR2）is proposed to calculate model mismatch by estimating the similarity of pressure measurements between each model and the benchmark model.Thus，the indexes of quantitative model accuracy are achieved.Furthermore，Fault Diagnosis Success Percen（tFDSP）is defined to calculate the effectiveness of leakage diagnosis.The leakage is diagnosed based on the models with different accuracy，and the effects of model accuracy on leakage diagnosis are obtained.Results illustrate that the effectiveness of this leakage diagnosis method is improved when the model becomes more accurate.When the refrigerant pipe network model accuracy is higher than 0.75，the FDSP is basically over 90%which shows that this leakage diagnosis is robust to model mismatch.

pipe network system；leakage diagnosis；pressure sensitivity analysis；model error；quantification of model accuracy；FlowMaster

U672.7

A

10.3969/j.issn.1673-3185.2016.06.018

2016-04-06

时间：2016-11-18 15:19

教育部新世纪优秀人才支持计划资助项目（NCET110189）；教育部高等学校博士点专项基金资助项目（20120142110078）

刘倩，女，1992年生，硕士生。研究方向：空调水系统特性及故障诊断徐新华（通信作者），男，1972年生，博士，教授。研究方向：舱室大气环境，空调水系统特性及故障诊断，建筑节能。E-mail：bexhxu@hust.edu.cn

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.036.html 期刊网址：www.ship-research.com

刘倩，张扬，徐新华，等.模型准确性对系统管网泄漏诊断的影响分析［J］.中国舰船研究，2016，11（6）：118-123. LIU Qian，ZHANG Yang，XU Xinhua，et al.Effect analysis of model accuracy on leakage diagnosis of pipe network system［J］.Chinese Journal of Ship Research，2016，11（6）：118-123.