轴承润滑特性对船舶推进轴系校中的影响

李正民，何琳，徐伟，何江洋

1海军工程大学振动与噪声研究所，湖北武汉 430033

2船舶振动噪声重点实验室，湖北武汉 430033

轴承润滑特性对船舶推进轴系校中的影响

李正民1，2，何琳1，2，徐伟1，2，何江洋1，2

1海军工程大学振动与噪声研究所，湖北武汉 430033

2船舶振动噪声重点实验室，湖北武汉 430033

径向轴承及推力轴承处边界条件的准确建立是船舶推进轴系校中计算的重点与难点。基于流体动压润滑理论，分析不同运行工况下考虑轴颈倾斜的径向轴承润滑特性，将轴承间隙、油膜厚度、支承基座及船体柔性以等效轴段挠度的形式计入轴系校中过程，并与刚性支承、弹性支承模型计算结果进行对比分析；计算因推力轴段转角、支承基座变形而引起的推力轴承附加力矩，并分析其对轴系校中的影响；建立轴承润滑与轴系校中耦合计算方法。结果表明：由径向轴承间隙、轴颈倾斜而引起的支点位置改变、润滑油膜厚度、推力轴承处附加力矩对轴系校中具有重要影响。

船舶推进轴系；校中；轴承支承；润滑油膜

0 引 言

船舶推进轴系校中是设计轴承轴向间距、径向变位以获得运转状态下合理的轴段应力及轴承反力的过程。良好的轴系校中状态是推进轴系安全、稳定运行的重要保证，校中状态不良的轴系将会引起轴段应力过大、轴承受力不均和磨损，以及轴系振动噪声过大等问题，严重影响船舶运行安全，且还将引起巨大的经济损失。

影响轴系校中的动态因素很多，其中轴承润滑油膜就是一项重要的影响因素［1］，因此，径向轴承及推力轴承处边界条件的确定成为轴系校中计算的重点与难点［2］。针对径向轴承边界条件的处理，文献［3-7］以流体动力润滑理论计算油膜刚度，并与弹性支承轴系校中模型进行了迭代计算，以寻求轴承润滑参数与校中计算参数相匹配的结果。但这与实际运行的径向轴承存在着差距：一是在实际情况中，滑动轴承与轴之间存在着间隙，在轴系运行过程中，油膜的形成将使轴系浮起，若忽略此间隙，在分析轴承变位与轴段挠度时将会产生误差，此外，文献［8］也指出忽略轴承间隙会把脱空的轴承误计算为负载荷，从而影响整个轴系的校中计算结果；二是动压润滑油膜的非线性决定了油膜刚度仅在小位移情况下可用，当轴承变位较大时，采用油膜刚度与轴承变位相乘的方法并不适合。此外，目前的轴系校中计算多未涉及推力轴承处的边界条件问题，而文献［9］指出，推力轴承处的附加力矩会影响轴系校中状态。为控制推进轴系纵向振动而提出的推力轴承弹性支撑隔振方案指出［10］，较大的螺旋桨推力势必引起推力轴承基座较大的偏斜，从而加剧推力轴承处附加力矩对轴系校中的影响。

针对上述问题，本文将总结轴系校中计算中径向轴承的建模方法，分析刚性支承和弹性支承（油膜刚度法）的不足，提出改进方法，并将径向轴承间隙、油膜厚度、支承基座及船体柔性以等效轴段挠度的形式计入轴系校中过程，对不同径向轴承建模方法进行对比分析。同时，计算因推力瓦块圆周方向分布不均、推力轴段转角或支承基座变形而引起的推力轴承附加力矩，并分析其对轴系校中的影响。

1 轴承支承建模方法

1.1 径向轴承建模方法

图1所示为轴系校中过程中径向轴承建模方法，其中图1（a）为刚性支撑模型，图1（b）为弹性性支撑模型，图1（c）为等效轴段挠度模型。

图1 径向轴承支承状态示意图Fig.1 Schematic of supporting state of journal bearing

1.1.1 刚性支承模型

如图1（a）所示，刚性支承模型可等效为在支点位置处的集中作用力R。径向轴承处的力平衡关系式为

式中：Q为剪力；下标L，R分别为单元的左、右端面。

传递矩阵表达式为

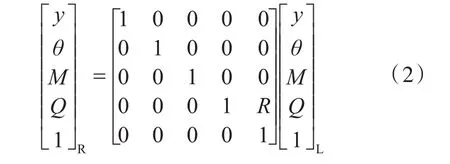
式中，单元端面的应力及应变状态矢量由挠度y、转角θ、弯矩M和剪力Q组成。

1.1.2 弹性支承模型

如图1（b）所示，当考虑到轴承油膜刚度ko、基座弹性kt与船体弹性kb时，一般将油膜刚度与基座及船体刚度视为串联弹簧，等效刚度ke见式（3）。

将轴承变位δ与轴段挠度y的差值看作等效弹簧的形变量，轴承的支反力由等效刚度及等效弹簧的形变量表达，力平衡关系见式（4）。

由式（4），可得此时传递矩阵表达式

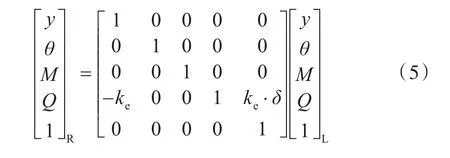
1.1.3 等效轴段挠度模型

轴承变位是以艉轴承中心线为参考线，各轴承中心线偏离参考线的距离。以往轴承刚性支撑模型多忽略轴承间隙，将轴承变位直接看作轴段挠度，例如，在轴承刚性支撑直线校中状态下，认为轴承处轴段的挠度为0、轴承变位亦为0。而如图2所示，当考虑轴承间隙时，轴承的变位应为此轴承间隙值Ci与艉轴承间隙值C1的差值δci。

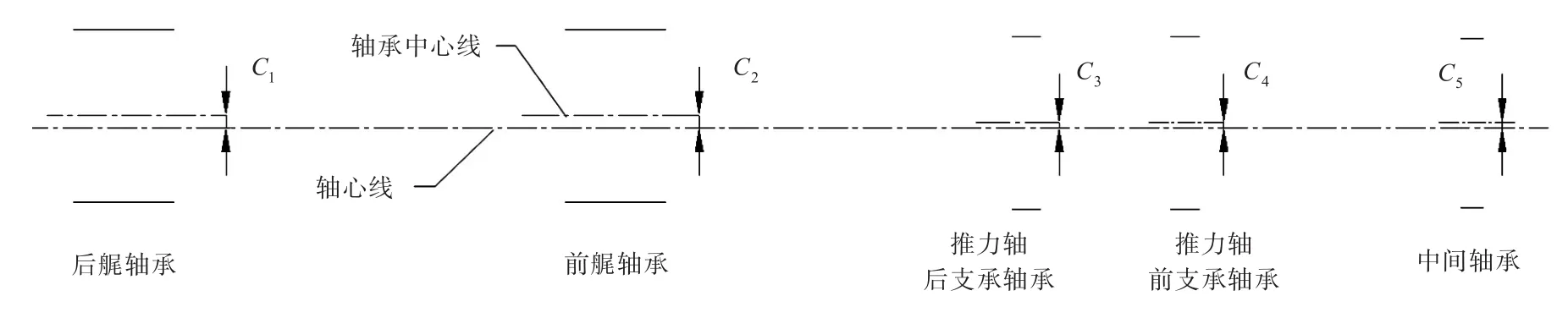
图2 考虑轴承间隙的轴承变位示意图Fig.2 Schematic of bearing vertical offsets considering the bearing clearance

因此，为了更准确地描述轴段挠度与轴承变位的关系，应引入轴承间隙修正量，即直线校中时轴承的变位值δci。

考虑到轴承间隙及不同运行工况下的润滑油膜特性，本文将以因油膜厚度而引起的轴段挠度变化量δo建立径向轴承模型，如图1（c）所示。δo可由稳态工况下的轴段偏心距e、偏位角φ计算，见式（7）。

此时，轴段等效挠度可由轴承变位与轴承间隙修正量的差值(δi-δci)、考虑支承基座船体弹性而产生的形变量δk以及由润滑油膜引起的轴段挠度变化量δo来表述。在轴系校中计算中，轴承支承的传递矩阵与式（2）相同，挠度由式（8）计算。

1.2 推力轴承处附加力矩模型

推力轴承内推力盘处的轴段转角或推力轴承支承基座的弹性变形，均可等效为如图3所示的推力盘偏斜。推力瓦块与推力盘之间的不平行将造成推力盘偏向一侧各瓦块油膜厚度变小、压力变大；推力盘偏离一侧各瓦块油膜厚度变大、压力变小；加之推力瓦块圆周方向的非均匀分布，因此油膜压力将在推力盘处产生附加力矩。在稳态情况下，可将上述垂直面内力矩用图4表述，其中M0为附加力矩。

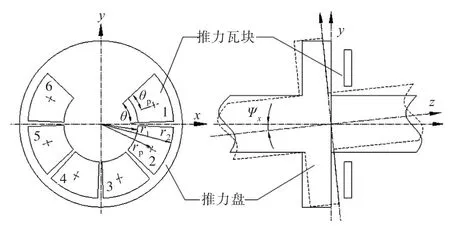
图3 推力轴承推力盘偏斜示意图Fig.3 Schematic of misalignment of thrust bearing

图4 推力盘处附加力矩Fig.4 Additional moment at the thrust collar

由力矩平衡方程式

可知推力盘附加力矩处的传递矩阵为

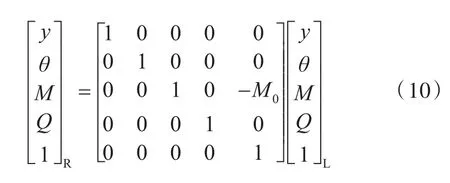
2 考虑润滑特性的轴系校中计算流程

图5所示为计入了轴承润滑特性的轴系校中计算流程图。计算流程分为3个部分，循环交叉运行。图中：方框1为基于传递矩阵法的轴系校

中计算；方框2为径向轴承润滑计算流程；方框3为推力轴承润滑计算流程。轴系校中计算为径向轴承润滑计算提供载荷参数和支点处轴段转角参数，为推力轴承润滑计算提供推力轴段转角参数；径向轴承润滑计算为校中计算提供考虑了轴承间隙、油膜厚度、支承基座及船体弹性变形的等效轴段挠度值以及径向轴承支点位置；推力轴承润滑计算为校中计算提供推力轴承附加力矩值。计算过程采取迭代计算的方法，当前、后2次计算所得径向轴承载荷、推力轴段转角的误差小于一定值时，迭代过程结束，润滑计算与校中计算达到稳定匹配值。

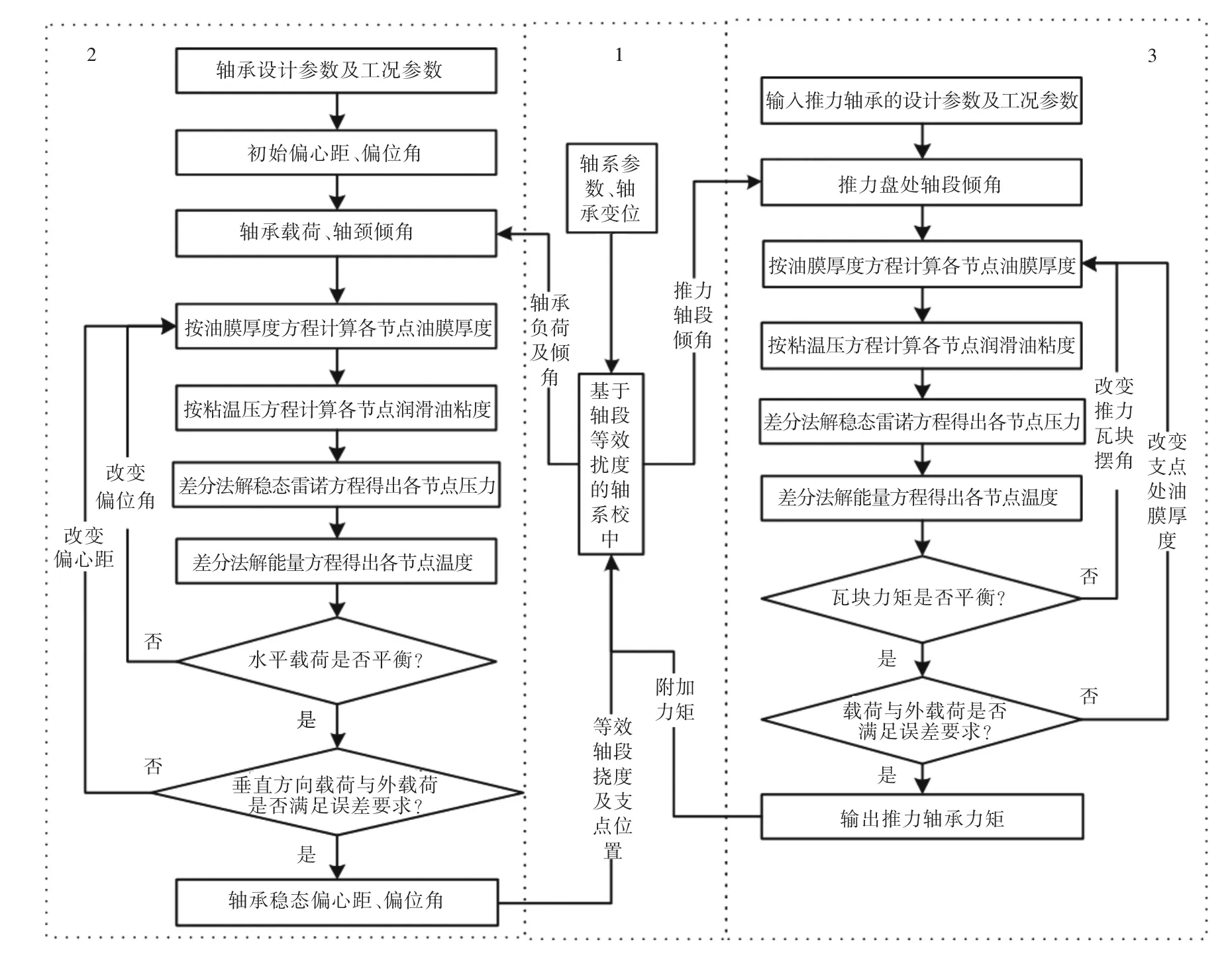
图5 考虑轴承润滑特性的轴系校中流程Fig.5 The flow chart of shaft alignment calculation considering the bearing lubrication characteristics

3 算例分析

3.1 轴系参数

图6所示为本文的推进轴系校中算例简图，由艉轴、2段推力轴以及中间轴组成。径向支承包括后艉轴承、前艉轴承、推力轴后支承轴承、推力轴前支承轴承及中间支承轴承，各轴承的参数如表1所示。

图6 轴系简图Fig.6 The diagram of the shaft

图6所示推力轴1处设置推力轴承，推力轴承

的参数如下：瓦块外径r2=0.302 5 m，瓦块内径r1=0.142 5 m ，瓦 块 数 z=6，支 点 处 半 径rp=0.225 m，瓦块包角θ0=0.698 1 rad，支点处角度θp=0.401 4 rad。

表1 径向轴承参数Tab.1 The parameters of journal bearings

3.2 径向轴承润滑特性

图7所示为载荷10 kN、转速110 r/min时不同轴颈倾斜时的后艉轴承油膜压力分布图，其中，图7（b）中的轴颈倾斜角度为3.50×10-4rad。表2～表4分别为不同轴颈倾斜、转速、载荷条件下的径向轴承等效支点位置L（p等效支点距离轴承后端面的距离）、由油膜厚度引起的轴段等效位移δo以及轴承润滑油膜刚度ko。

图7 艉后轴承润滑油膜压力分布Fig.7 The distribution of the oil film pressure of the stern tube bearing

表2 支点位置、等效位移、油膜刚度与轴颈倾斜的关系Tab.2 The relationship of Lp，δo，kowith misalignment

表3 支点位置、等效位移、油膜刚度与转速的关系Tab.3 The relationship of Lp，δo，kowith shaft speed

由图7（a）可知，当轴颈未发生倾斜时，油膜压力沿轴承长度方向分布均匀，结合表2可知，油膜力作用点的位置在轴承中点处；随着轴颈倾斜角的增大，轴承压力在轴承长度方向的分布开始不均，油膜承载区、等效支点向船艉方向移动。

由表2可知，随着轴颈倾斜角ψx的增加，轴段等效位移δo略有增加。由表3和表4可知，δo受转速n、轴承负荷F影响的灵敏度较高，且变化趋势与润滑油膜厚度的变化一致，即随轴承转速的提高而增加，随轴承负荷的增加而减小。

算例中，艉轴承垂直方向油膜刚度ko的数量级为107～108N/m，且油膜刚度随轴倾斜的增加而减小，随轴转速的升高而减小，随载荷的加大而变大，其变化趋势与润滑油膜厚度的变化相反，即油

膜厚度越大，刚度越小，反之，油膜厚度越小，刚度越大。

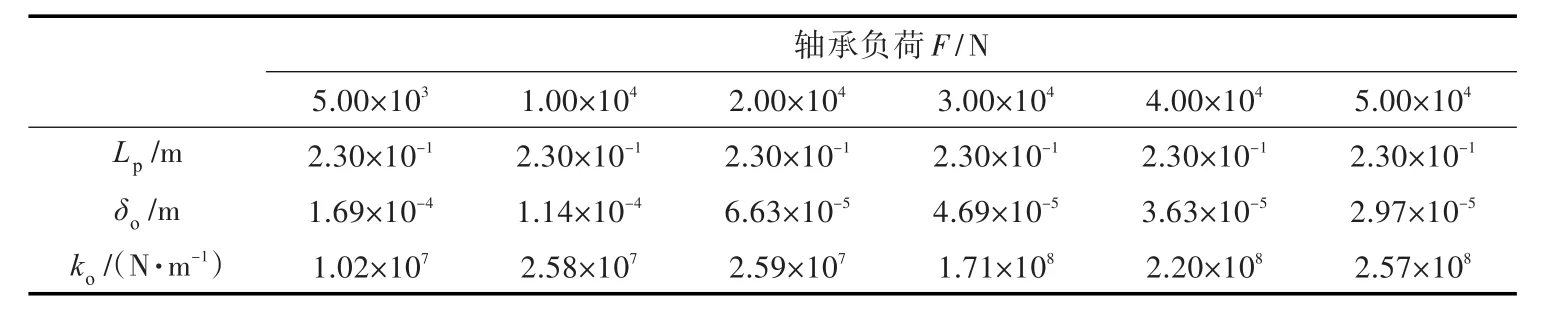
表4 支点位置、等效位移、油膜刚度与承载力的关系Tab.4 The relationship of Lp，δo，kowith load

3.3 推力轴承的润滑特性

图8所示为推力150 kN、转速110 r/min时的推力轴承多瓦稳态润滑油膜压力分布，其中，图8（b）中推力盘的倾斜角度为1.00×10-4rad。由图可知，轴颈倾斜或基座的变形将造会成推力瓦块与推力盘之间的不平行，推力盘偏向一侧各瓦块的油膜厚度变小、压力变大；推力盘偏离一侧各瓦块的油膜厚度变大、压力变小。因瓦块周向分布的不对称，以及瓦块压力分布的不同而引起的图8（a）和图8（b）中的附加力矩分别为1.030×104和1.867×104N·m。

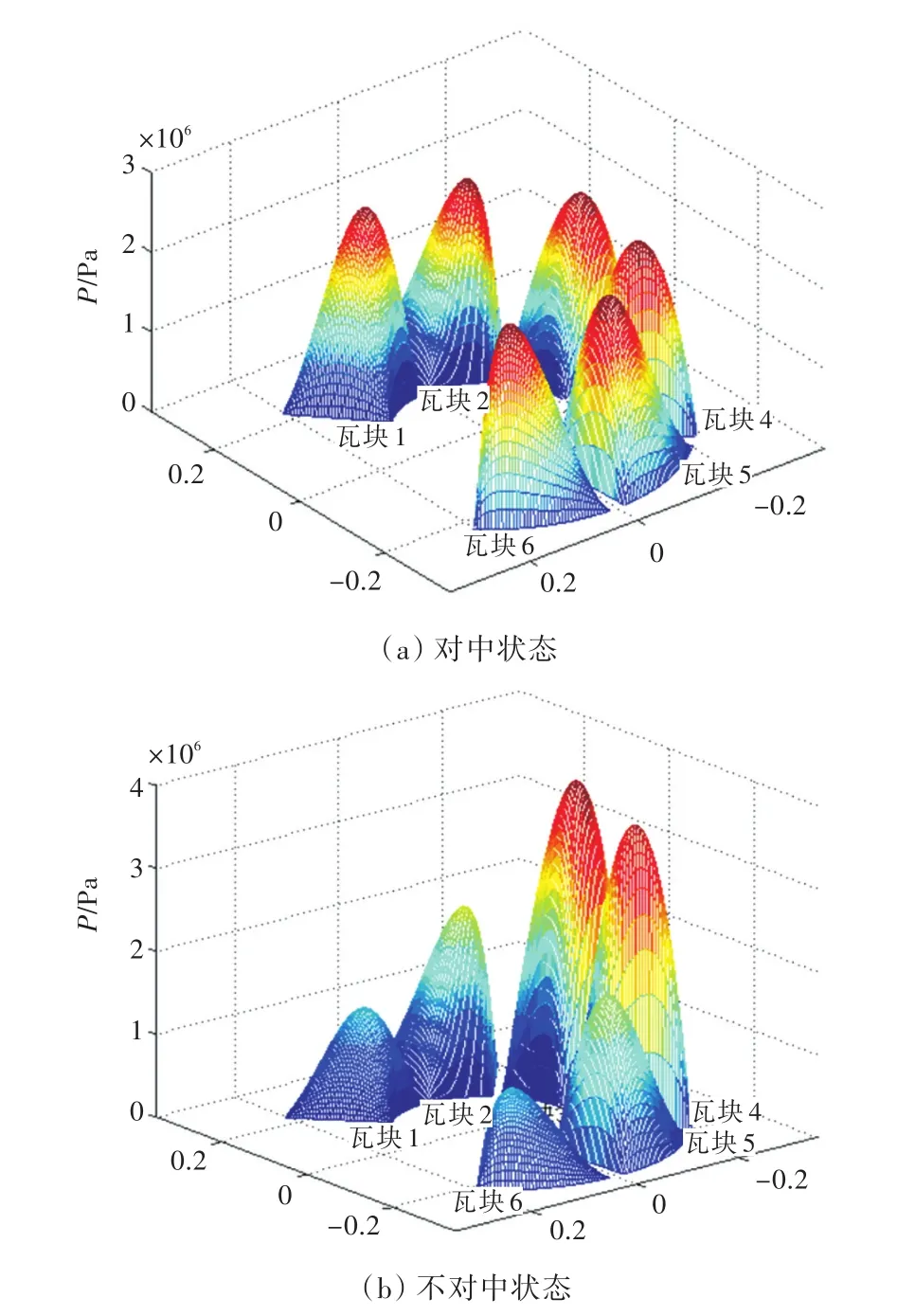
图8 推力轴承多瓦稳态润滑油膜压力分布Fig.8 The distribution of the oil pressure of thrust bearing

3.4 推进轴系校中计算

图9（a）为轴承支反力，其中横坐标为轴承编号；图9（b）～图9（e）分别为轴段挠度、转角、弯矩和剪力图，其中横坐标为轴段坐标。图9（a）～图9（e）中，图例中的数字1～5分别代表下面的5种计算方法。

图9 不同轴承支承状态下轴系校中计算Fig.9 Alignmet calculation results under differe supporting conditions

方法1：刚性支承；

方法2：弹性支承（ke1=4×107N/m，ke2=5× 107N/m，ke3=6×108N/m，ke4=6×108N/m，ke5=3× 108N/m）；

方法3：弹性支承，各等效刚度为方法2的2倍；

方法4：等效轴段挠度法；

方法5：等效轴段挠度法并考虑推力轴承处的附加力矩。

由图9（a）可知，与方法1的刚性支承相比，在方法2的弹性支承假设下，1，2，5号轴承的承载力变化不大，3号轴承的承载力有明显的增大，4号轴承的承载力有明显的减小。因为在相同的基座船体刚度条件下，4号轴承较大的承载力使得基座产生的弹性变形较大，即轴段挠度较大，而3号轴承较小的承载力产生较小的基座弹性变形，导致4号轴承的向下变位较大、3号轴承的向下变位较小，从而使得4号轴承的承载力下降、3号轴承的承载力上升。通过比较图9（a）～图9（e）中的方法3与方法2可知，当各轴承等效支承刚度变大时，轴承反力、轴段挠度、转角、弯矩和剪力都向着刚性支承的结果靠近，可以预测，当轴承支承刚度达到一定值时，等同于刚性支承。

方法4为采用本文所建立径向轴承模型所得的轴系校中计算结果。由图9（d）和图9（e）可知，考虑了轴颈倾斜的后艉管支点位置将向后移动，结合图9（c）可知，支点位置的后移会引起轴段转角变小。由图9（b）可知，由考虑了等效挠度的校中方法所得的轴段挠度较刚性支承而言偏向上，而弹性支承假设则偏向下。以后艉轴承为例，当承载力为1×104N时，由于因油膜厚度引起的等效变位为向上1.165 0×10-4m，大于由考虑了支承基座弹性形变量所引起的轴段向下等效变位2.176 0× 10-5m，因此径向轴承等效位移的建模方法更能准确反应轴系运行过程中的实际状态。

方法5为考虑了推力轴承附加力矩后的轴系校中计算结果，由图9（d）可知，考虑附加力矩后，在推力盘处，即轴系7.2 m处弯矩出现了明显的峰值。对比图9（a）中的方法5和方法4，发现由于考虑了推力轴承附加力矩的作用，3号轴承脱空、承载力为0，而4号轴承的承载力则进一步增大；结合图9（b）可知，此时3号轴承处的轴段等效位移为2.048×10-4m，小于轴承间隙C3=3×10-4m，即轴段未与轴承上表面接触，因此3号轴承脱空，而并非为负载荷；由船军标CB/Z 338-2005［11］可知，轴承负荷应不小于相邻两跨距间所有重量总和的20%，因此，考虑推力轴承处的附加力矩后，3号轴承并不能满足要求，应优化轴系布置，让轴系在运行过程中使轴承受力满足要求。可以预测，当轴系反转时，推力反向，推力轴承处附加力矩的方向也会改变，从而将引起3号轴承承载力变大，4号轴承承载力变小。

4 结 语

在船舶推进轴系校中计算分析中，径向、轴向边界条件的确定具有重要的理论研究价值。以往，径向轴承间隙及推力轴承处的附加力矩在校中计算中并未得到关注，且径向轴承的刚性支承、弹性支承模型不能反映轴承润滑油膜厚度特性。本文针对船舶轴系动态校中计算过程中的上述问题，研究了径向、推力轴承润滑特性对轴系校中的影响。以等效轴段挠度的形式将轴承间隙、油膜厚度计入轴系校中过程，此方法能更准确地表述轴承变位与轴段挠度的关系；考虑推力轴承处的

边界条件问题，计入因推力轴承瓦块全圆周非均匀分布、推力轴段转角、推力轴承基座变形而产生的附加力矩作用，可以更为全面地考虑校中影响因素，为推力轴承弹性支撑减振方案提供合理的轴系校中评估方法。在轴系校中设计过程中考虑轴承润滑特性，优化设计轴承间距和轴承变位，对轴系校中施工以及保持轴系安全具有积极的意义。

［1］ 陆金铭，周海港，顾卫俊，等.船舶轴系动态校中轴承油膜的影响计算［J］.船舶工程，2009，31（6）：69-72. LU Jinming，ZHOU Haigang，GU Weijun，et al.Calculation of the influences of marine shafting dynamic alignment affected by bearing oil film［J］.Ship Engineering，2009，31（6）：69-72.

［2］ TUPKARI P D，SHARMA P K.Shaft alignment in ship［J］.International Journal of Advanced Technology in Engineering and Science，2014，2（5）：325-331.

［3］ 耿厚才.船舶轴系的动态校中计算［J］.中国造船，2006，47（3）：51-56. GENG Houcai.Dynamic alignment calculations for marine shafting［J］.Shipbuilding of China，2006，47（3）：51-56.

［4］ 周瑞平.超大型船舶推进轴系校中理论研究［D］.武汉：武汉理工大学，2005：101-117. ZHOU Ruiping.The theoretic studies on the propulsion shafting alignment of ultra-large vessels［D］.Wuhan：Wuhan University of Technology，2005：101-117.

［5］ MURAWSKI L.Shaft line alignment analysis taking ship construction flexibility and deformations into consideration［J］.Marine Structures，2005，18（1）：62-84.

［6］ MURAWSKI L.Influence of journal bearing modeling method on shaft line alignment and whirling vibrations［C］//Proceedings of the 8th International Symposium on Practical design of Ships and Other Floating Structures.Shanghai，China，2001.

［7］ MITSUI J，AKUTSU Y.Analysis of shaft alignment taking oil film characteristics of stern tube bearing into consideration：Part 1，theoretical analysis［J］.Bulletin of JSME，1984，27（224）：317-324.

［8］ SVERKO D.Design concerns in propulsion shaft alignment［C］//Proceedings of the ICMES Conference.Helsinki：［s.n.］，2003.

［9］ LARSEN O C.Some considerations on marine shafting design［J］.Industrial Lubrication and Tribology，1981，33（5）：164-171.

［10］ 何江洋，何琳，帅长庚，等.船舶动力设备及推力轴承集成隔振系统设计［J］.舰船科学技术，2013，35（1）：77-81. HE Jiangyang，HE Lin，SHUAI Changgeng，et al.Design research of integrated vibration isolation system for marine power equipment and thrust bearing［J］. Ship Science and Technology，2013，35（1）：77-81.

［11］ 国防科学技术工业委员会.船舶推进轴系校中：CB/ Z 338-2005［S］.北京：中国标准出版社，2006. Commission of Science，Technology and Industry for National Defence.Propulsion shaft alignment of ship：CB/Z 338-2005［S］.Beijing：China Standard Press，2006.

The influence of bearing lubrication characteristics on marine propulsion shaft alignment

LI Zhengmin1，2，He Lin1，2，XU Wei1，2，HE Jiangyang1，2

1 Institute of Noise and Vibration，Naval University of Engineering，Wuhan 430033，China

2 National Key Laboratory on Ship Vibration and Noise，Wuhan 430033，China

The configuration of the boundary conditions of journal and thrust bearings is one of the most important and difficult parts of the procedure of marine propulsion shaft alignment.Based on the hydrodynamic lubrication theory,the lubrication performance of journal bearings is analyzed with consideration to misalignment.The equivalent deflection of the shaft element obtained from the bearing clearance,the lubricating oil film thickness and the elasticity of the supporting structure are proposed during shaft alignment calculation,and the results of the alignment calculation using the equivalent deflection of the shaft element are compared with the scenarios of the stiff support hypothesis and linearly elastic support hypothesis.The bending moment acting on the thrust collar resulting from the misalignment or uneven distribution of the thrust pads in the circumferential direction is calculated,the influence of the additional moment on the shaft alignment is analyzed,and the coupling procedure of the shaft alignment calculation and bearing lubrication performance calculation is established.The results show the important influences of bearing clearance,lubricating oil film thickness and additional moment on shaft alignment.

marine propulsion shaft；alignment；bearing support；lubricating oil film

U664.21

A

10.3969/j.issn.1673-3185.2016.06.016

2016-03-09

时间：2016-11-18 15:19

国家部委基金资助项目；湖北省自然科学基金资助项目（2014CFB233）

李正民，男，1987年生，博士生。研究方向：船舶推进轴系校中及振动。E-mail：lizhengm100@163.com徐伟（通信作者），男，1980年生，博士，副研究员。研究方向：船舶机械设备减隔振技术。E-mail：xuwei216@126.com

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.032.html 期刊网址：www.ship-research.com

李正民，何琳，徐伟，等.轴承润滑特性对船舶推进轴系校中的影响［J］.中国舰船研究，2016，11（6）：104-111. LI Zhengmin，He Lin，XU Wei，et al.The influence of bearing lubrication characteristics on marine propulsion shaft alignmen［tJ］.Chinese Journal of Ship Research，2016，11（6）：104-111.