基于PSO-LSSVM的干旱区中长期降水预测模型研究

孟锦根

(四川交通职业技术学院 建筑工程系，成都 611130)



基于PSO-LSSVM的干旱区中长期降水预测模型研究

孟锦根

(四川交通职业技术学院 建筑工程系，成都 611130)

降水量的准确预测对于干旱地区的水资源综合利用、抗旱减灾有重要意义。引入基于粒子群算法进行参数寻优的最小二乘支持向量机模型(PSO-LSSVM)，构建考虑7a周期的年降水样本及考虑季节性特征的月降水样本，建立干旱区年、月尺度下的中长期降水预测模型，并应用新疆阿勒泰地区1960—2013年实测降水序列，验证模型的适用性。结果表明：基于粒子群算法与最小二乘支持向量机的中长期降水预测模型预测精度高，泛化能力强，能有效地预测新疆阿勒泰地区年、月降水量。该模型为干旱区中长期降水预测提供了一种可靠的研究思路与方法。

粒子群算法；最小二乘支持向量机；干旱区；阿勒泰地区；降水预测

1 研究背景

降水是区域水循环的重要组成部分，降水量规律及预测研究对于干旱地区水资源的合理开发利用、生态环境的改善和灾害控制具有重要意义[1]。近半个世纪以来，对于干旱区降水规律的研究较多，如于淑秋等[2]对我国西北地区近50a的降水序列研究发现1986年存在明显的降水量跃变点；刘彩红[3]利用多种水文统计分析方法对新疆近45a的气候特征进行研究；鞠彬等[4]对新疆额尔齐斯河流域1962—2013年间降水特征及趋势进行研究。近年来，随着机器学习理论、人工智能算法的发展，出现了许多用于分析复杂非线性关系的模型，如人工神经网络模型[5]、随机森林[6]、贝叶斯网络模型[7]等，运用相关人工智能模型进行地区降水预测逐步成为热点问题之一，如韩焱红等[8]利用贝叶斯理论进行集合降水概率预报；甄亿位等[9]利用随机森林及人工神经网络对南京市中长期降水预报模型进行研究。但上述人工智能模型普遍存在过学习、收敛速度慢、稳健性不足等问题，需要进一步改进和完善。而最小二乘支持向量机模型由于收敛快以及优异的拟合能力，已经在信息、医学、生物等领域取得广泛的应用，但在水文学领域，特别是在干旱半干旱地区的降水预测研究中却鲜有出现。鉴于此，本文选取典型干旱区新疆阿勒泰地区作为研究区域，利用气象站1960—2013年的逐日降水序列资料，构建基于粒子群算法与最小二乘支持向量机的年、月尺度下的中长期降水量预测模型，并检验分析其预测效果，以望为今后中长期降水预报研究提供一种新的思路与方法。

2 研究区域概况及数据来源

新疆阿勒泰地区位于新疆维吾尔自治区的最北部(东经85°35′～90°30′，北纬46°52′～49°15′)，具有典型的大陆性干旱气候特征，温差变化大，降水量很少[10]。新疆是中国5大牧区之一，阿勒泰地区又是新疆最主要的牧区之一，选取阿勒泰这一典型干旱区进行流域内降水量的模拟预测研究，对地区水资源管理、防旱抗灾、发展节水灌溉及确定合理的灌溉制度具有重要的意义[11]。

本文选取阿勒泰地区阿勒泰气象站(47°44′N，88°05′E)1960—2013年的逐日降水资料进行中长期降水量模拟研究，降水资料来源于国家气象资料共享中心网，将逐日降水序列整理为月降水样本序列及年降水样本序列供模型模拟预测。

3 模型构建与研究方法

3.1 模型构建

3.1.1 最小二乘支持向量机

支持向量机(SVM)是由Vapnik提出的一种能够处理回归和模式识别等诸多问题的新型统计学方法[12]，能较好地解决以往学习方法中存在的过学习、非线性、局部极值点以及高维数等实际问题[13]。

最小二乘支持向量机算法(LS-SVM)于2001年由Suykens等[14]提出，其优化指标采用平方项，将传统支持向量机中的不等式约束改为等式约束，把二次规划问题转化成线性方程组的求解问题，简化了模型计算的复杂性。最小二乘支持向量机原理如下所述。

设样本为n维向量，某区域l个样本(x1，y1)，(x2，y2)，…，(xl，yl)∈Rn×R，采用非线性映射将样本从原空间Rn映射到特征空间φ(xi)，并在这个高维特征空间中构造最优决策函数，即

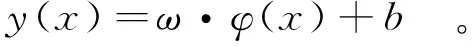
(1)

定义优化问题为

(2)

式中：c为惩罚因子；ei为不敏感损失函数的松弛因子；b为偏差量；ω为非负常数，称为惯性权重。

利用拉格朗日法求解上述优化问题，即

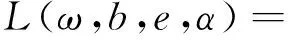
(3)

式中αi为Lagrange乘子。

根据最优条件，并定义核函数为K(xi,xj)=φ(xi)T·φ(xj)，将二次规划问题转化为求解线性方程组，即

(4)

利用最小二乘法求α，b。得到LS-SVM模型为

(5)

其中核函数采用RBF函数，即

(6)

式中σ为核函数宽度参数。

3.1.2 粒子群优化算法

模型预测精度的高低，与模型参数的取值有密不可分的关系，本文采用粒子群优化算法(PSO)对LS-SVM模型参数c和σ进行优选。

粒子群优化算法(PSO)是由Eberhart等[15]提出的一种群智能算法，具有很强的全局寻优能力。粒子群优化算法原理如下所述。

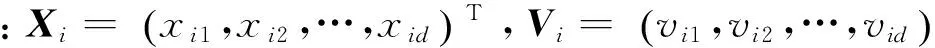
(7)

(8)

式中：c1，c2为学习因子，一般c1=c2；rand( )为介于(0，1)之间的随机数。

本文采用的粒子群算法及最小二乘支持向量机模型皆由MATLAB中编程计算完成，PSO-LSSVM模型具体算法流程如图1所示。

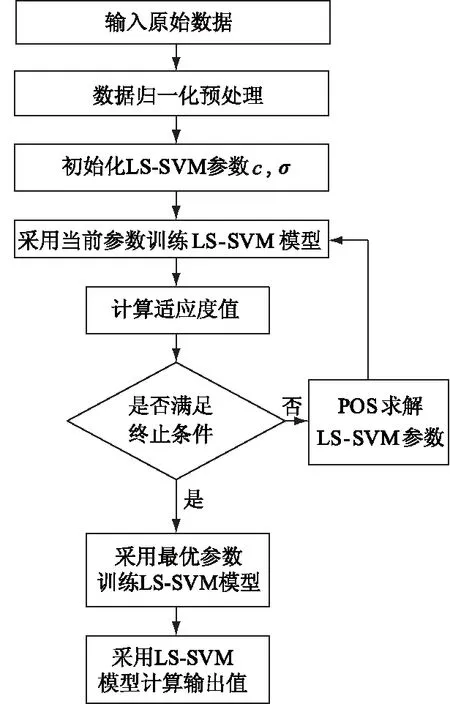
图1 PSO-LSSVM模型算法流程Fig.1 Algorithm flow chart of PSO-LSSVM model

3.2 研究方法

3.2.1 年尺度研究

利用年降水时间序列构建基于粒子群算法与最小二乘支持向量机的中长期年降水预测模型，即利用前N年年降水数据预测N+1年的年降水。根据鞠彬等[4]研究，阿勒泰地区年降水时间序列以7a内的周期变化最为明显。因此本次研究选择采用前7a的降水预测第8年的降水。以阿勒泰站1960—2003年的年降水序列作为训练期样本，2004—2013年的年降水序列作为检验期样本。

3.2.2 月尺度研究

考虑到降水序列在月时段体现不同的特征，将季节性因子引入到中长期降水预测模型中，形成考虑季节因子的月尺度PSO-LSSVM降水预测模型。

设有N年逐月实测降水系列资料为

(9)

式中Qi,j为第i年第j月的降水量。

由于降水变化的趋势性，降水Qi,j与前期的降水量有关，考虑降水变化的季节性规律，降水Qi,j又与历史同时期的降水量有关。PSO-LSSVM模型的预测因子个数对训练结果有较大的影响，个数过少，则没有足够的信息去让LS-SVM捕捉；若个数过多，则会引入过多的噪声，不仅增加模型训练时长，而且可能会干扰训练结果。研究表明，一般取前期2～3个月的月降水和历史同期2～3个月的月降水数据作为预测因子较为合适。

3.3 评价指标

本次研究采用平均相对误差(RME)、相关性系数(R2)、确定性系数(Dy)3个指标来衡量模型预测值与实测值之间的拟合精度。根据水文情报预报相关规范作为标准[16]，以实测值的±20%为许可误差，确定性系数在0.7以上。各统计量的具体公式如下：

(10)

(11)

(12)

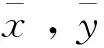
4 结果与分析

4.1 年尺度下降水量预测

分别统计训练期、检验期PSO-LSSVM模型精度指标，具体评价结果见表1，阿勒泰地区年降水模拟预测过程见图2。年尺度PSO-LSSVM模型在预测期的平均相对误差为10.94%，确定性系数为0.747，相关系数为0.801，平均相对误差未超过训练期平均相对误差12.11%，说明年尺度PSO-LSSVM模型的泛化性较好且预测精度较高；从图2也可以看出，2004—2013年预测结果与实测降水过程较为接近。根据水文情报预报相关规范，以实测值的±20%为许可误差，则预测期的样本合格率为90%，说明年尺度PSO-LSSVM模型能有效地预测年降水量的变化趋势，能合理准确地预测年降水量。

表1 训练期与预测期PSO-LSSVM模型精度分析

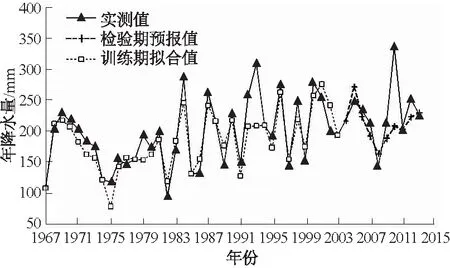
图2 阿勒泰地区年降水实测与模拟预测对比Fig.2 Comparison between measurement and simulation of annual precipitation in Altay region

图3为降水距平百分率与模型模拟预测误差关系图。根据地区旱涝等级划分，年降水距平百分率在±25%范围内的都为正常降水年份。

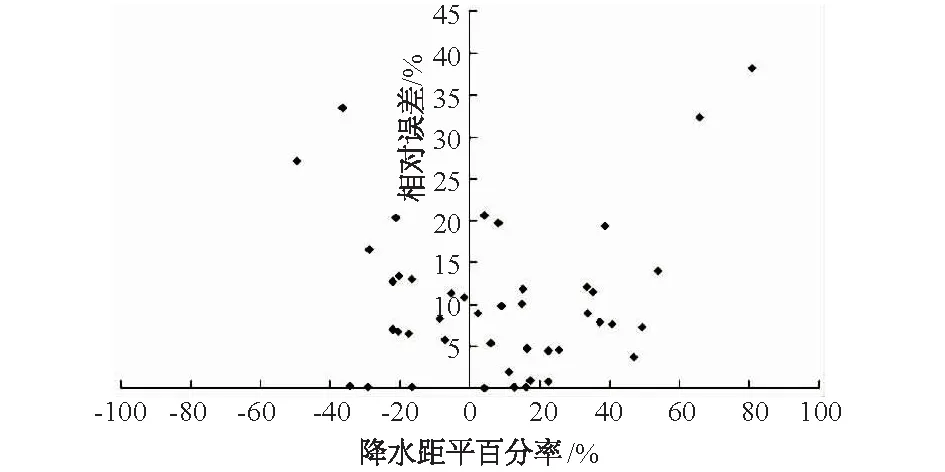
图3 降水距平百分率与模型模拟预测误差关系Fig.3 Relationship between precipitation anomaly percentage and simulation and forecasting error

由图3可以看出，在降水正常年份，模型模拟预测精度皆在±20%范围内，预测效果较为理想。但在大涝大旱年份，年尺度PSO-LSSVM模型预测精度误差较大，特别对于极端大降雨的预测效果不太理想，很大程度上影响了PSO-LSSVM模型整体的精度评价。对干旱地区而言，关注降水偏旱年份要比干旱区发生降水极端偏大年份更为重要，而从图3可以看出，偏旱年份预测精度整体要比偏涝年份预测精度好，这在干旱地区降水预测中是较为有利的，说明年尺度PSO-LSSVM模型在干旱地区有较好的适用性和应用前景。

4.2 考虑季节因素的月尺度降水量预测

选取阿勒泰地区1960—2013年实测逐月降水资料为研究对象。以1960—2010年的月降水序列作为PSO-LSSVM模型的训练期样本，以2011—2013年的降水序列作为检验期样本。通过试验研究得出考虑季节因子的月尺度PSO-LSSVM模型的输入因子的个数为4，即分别取前期2个月的月降水和历史同期2个月的月降水作为重构降水序列，模型的预测结果最优。

月尺度PSO-LSSVM模型在检验阶段(2011—2013年)预测结果分别如表2和图4所示。

表2 月降水检验阶段预测结果对比

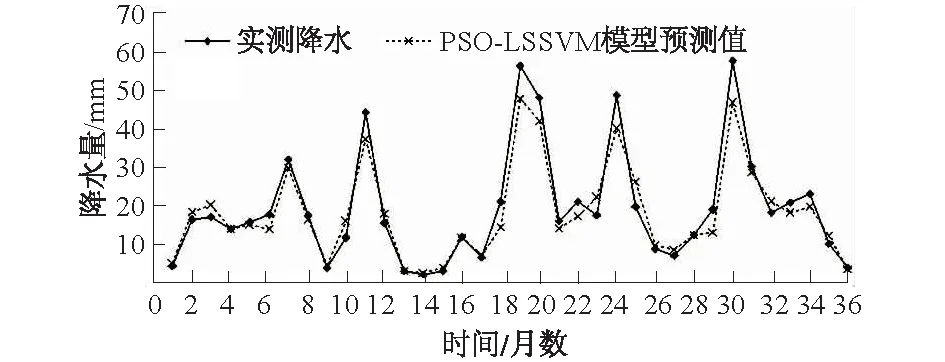
图4 月降水量检验期实测值和预测值对比Fig.4 Comparison of monthly precipitation between measured and forecast values in inspection period

由表2和图4可以看出，考虑季节因子的月尺度PSO-LSSVM模型检验期平均相对误差为15.9%，相对误差低于20%的分别有27个，占样本总数的75%，相对误差低于30%的分别有31个，占样本总数的86%。可以看出，考虑季节因子的月尺度PSO-LSSVM模型预测结果较为可靠，在阿勒泰地区有较好的适用性。

在降水较多的月份，PSO-LSSVM模型预测误差普遍为负值，出现降水预测偏少的情况，可见PSO-LSSVM模型对于极端大降雨的预测效果不太理想。考虑是由于同月不同年份降水的随机性大，预测值曲线波动较大，呈现不稳定的状态，这样容易产生较大的预测误差，后期考虑加入大气环流因子进行共同预测，有望提高模型的预测精度。在降水较少的月份，考虑季节因子的月尺度PSO-LSSVM模型的曲线比较平滑、稳定，相对误差普遍较小，PSO-LSSVM模型对降水偏旱点预测较为准确，可见同期降水量的相关性好，增加同期降水因子使得预报效果显著变好。

考虑到研究区域为干旱地区，极端大降水情景不如偏旱降水年份对地区影响大，所以尽管月尺度PSO-LSSVM模型对于大降水月份预测精度不高，但从平均相对误差、合格率和确定性系数，以及偏旱点高预测精度的角度考虑，考虑季节因子的月尺度PSO-LSSVM模型在干旱地区依然有较好的适用性。

5 结 论

(1) 本文基于粒子群算法与最小二乘支持向量机构建了年尺度、月尺度下的中长期降水预测模型(PSO-LSSVM)，并应用新疆阿勒泰地区1960—2013年实测降水资料进行分析研究。结果表明中长期降水预测模型精度高，能有效地预测年尺度与月尺度降水，在阿勒泰地区有较好的适用性，为其他干旱区中长期降水的预测研究提供了一种新的观点和途径。

(2) 与其他中长期预测模型相比，PSO-LSSVM模型具有精度高、收敛快、泛化能力强等优势，今后将会得到更大范围的推广与应用。本文研究的中长期降水预测模型对于极端大降雨的预测效果不太理想，后期考虑加入大气环流因子进行预测，有望提高PSO-LSSVM模型的预测精度，同时可以考虑引入其他相关中长期预报方法进行结合，有待进一步研究。

[1] 于海姣, 温小虎, 冯 起,等. 基于支持向量机(SVM)的祁连山典型小流域日降水-径流模拟研究[J]. 水资源与水工程学报, 2015，(2):26-31.

[2] 于淑秋，林学椿，徐祥德.我国西北地区近50年降水和温度的变化[J].气候与环境研究，2003，8(1): 9-18.

[3] 刘彩红. 近45a新疆气候特征及异常研究[D]. 南京：南京信息工程大学, 2008.

[4] 鞠 彬, 张帅挺, 胡 丹. 额尔齐斯河流域气候变化特征分析[J]. 长江科学院院报, 2015, 32(9):21-25.

[5] 王文圣，丁 晶，刘国东.人工神经网络非线性时序模型在水文预报中的应用[J].四川水力发电，2000，19(增刊):8-10.

[6] 廖 杰，王文圣，李跃清，等.支持向量机及其在径流预测中的应用[J].四川大学学报(工程科学版)，2006，38(6):24-28.

[7] 慕春棣，戴剑彬，叶 俊.用于数据挖掘的贝叶斯网络[J].软件学报，2000，11(5): 660-666.

[8] 韩焱红, 矫梅燕, 陈 静,等. 基于贝叶斯理论的集合降水概率预报方法研究[J]. 气象, 2013, 39(1):1-10.

[9] 甄亿位, 郝 敏, 陆宝宏,等. 基于随机森林的中长期降水量预测模型研究[J]. 水电能源科学, 2015(6)：6-10.

[10]鞠 彬，胡 丹.参考作物蒸发蒸腾量计算方法在额尔齐斯河流域的适用性研究[J]. 水资源与水工程学报，2014，25(5):106-111.

[11]廖显琴，李 毅.参考作物腾发量计算方法的适用性研究[J].灌溉排水学报，2009，28(6): 14-17.

[12]VAPNIK V N. The Nature of Statistical Learning Theory[M].New York: Springer, 1995.

[13]VAPNIK V N. An Overview of Statistical Learning Theory[J]. IEEE Transactions of Neural Network, 1999, 10(5): 988-999.

[14]SUYKENS J A K, GESTEL T V, BRABANTER J D,etal. Least Squares Support Vector Machines[M]. Singapore: World Scientific Publishing Co., 2002.

[15]KENNEDY J, EBERHART R. Particle Swarm Optimization[C]∥Proceedings of IEEE International Conference on Neural Networks, Piscataway, NJ. December 1, 1995: 1942-1948.

[16]水利部水文局. 水文情报预报技术手册[M]. 北京：中国水利水电出版社, 2010.

(编辑：姜小兰)

Model of Medium-long-term Precipitation Forecasting inArid Areas Based on PSO and LS-SVM Methods

MENG Jin-gen

(Department of Architectural Engineering, Sichuan Vocational and Technical College of Communications, Chengdu 611130, China)

Precipitation forecasting in arid region is of great significance for water resources utilization and drought disaster reduction. A precipitation forecasting model in yearly and monthly scales based on particle swarm algorithm (PSO) and least squares support vector machine (LSSVM) model was established using the annual precipitation sample of a seven-year cycle and the monthly precipitation sample of seasonal characteristics. The applicability of the model was verified through the measured precipitation sequence from 1960 to 2013 in Altay region. Results show that the model based on PSO and LSSVM could effectively forecast the annual and monthly precipitation in Altay region, hence is of high precision and strong generalization ability. It offers a reliable research idea and method for medium and long-term precipitation forecast in arid areas.

PSO; LS-SVM; arid areas; Altay region; precipitation forecasting

2016-01-06;

2016-03-21

孟锦根(1970-)，男，四川中江人，讲师、高级工程师，主要从事智能算法方向的研究，(电话)18190846570(电子信箱)504862652@qq.com。

10.11988/ckyyb.20160010

2016,33(10):36-40

P338.9

A

1001-5485(2016)10-0036-05